Постулаты классической механики

1.

2. ПОСТУЛАТЫ КЛАССИЧЕСКОЙ МЕХАНИКИ
Первый закон Ньютона (закон инерции) постулирует и содержит
определение инерциальной системы отсчета (ИСО)
Существуют
такие
системы
отсчета,
называемые
инерциальными, относительно которых тело (МТ) движется
прямолинейно и равномерно либо покоится, если отсутствуют
какие бы то ни было воздействия на нее со стороны других
материальных точек или тел.
Т.о., свободная МТ либо покоится относительно ИСО,
либо движется по инерции, и это движение в ИСО – равномерное
и прямолинейное.
Второй закон Ньютона гласит:
Ускорение, приобретаемое материальной точкой массы под
действием силы , сонаправлено с силой, а величина его прямо
пропорциональна величине силы и обратно пропорциональна
массе материальной точки:
F
a b
m
(2.1)
где b=const – положительная постоянная, зависящая от выбора
системы единиц.

2.

В системе СИ b=1 и второй закон можно записать в форме
уравнения движения для МТ:
(2.1 а)
ma F
Если на материальную точку действуют не одна сила, а несколько
сил, то
n
ma
Fk
(2.1 б)
k 1
Третий закон Ньютона описывает взаимодействие двух тел (МТ).
При взаимодействии двух тел (МТ) силы, которыми они
действуют друг на друга, равны по величине и противоположны
по направлению:
F1,2 F2 ,1
где
F- 1,2
F2,1
(2.2)
сила, действующая на тело 1 со стороны тела 2,
сила, действующая на тело 2 со стороны тела 1.

3.

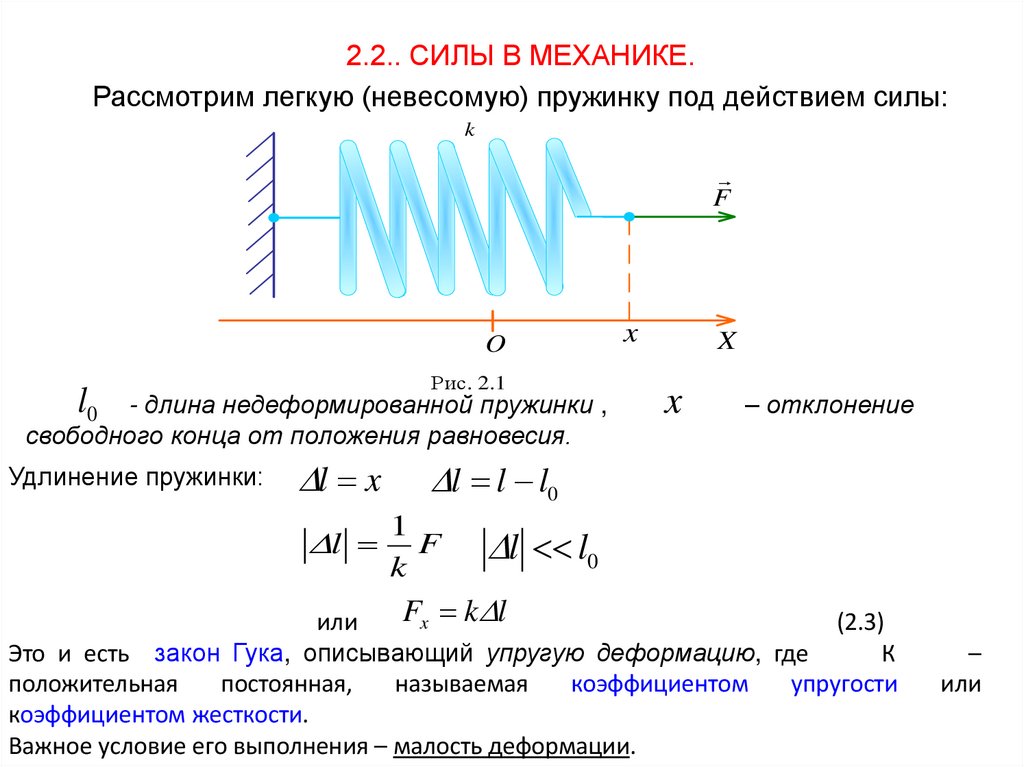
2.2.. СИЛЫ В МЕХАНИКЕ.
Рассмотрим легкую (невесомую) пружинку под действием силы:
k
F
O
Рис. 2.1
l0
- длина недеформированной пружинки ,
свободного конца от положения равновесия.
Удлинение пружинки:
l x
l
x
X
x
– отклонение
l l l0
1
F
k
l l0
Fx k l
или
(2.3)
Это и есть закон Гука, описывающий упругую деформацию, где
К
положительная
постоянная,
называемая
коэффициентом
упругости
коэффициентом жесткости.
Важное условие его выполнения – малость деформации.
–
или

4.

СИЛА ТРЕНИЯ
Трение, которое мы рассмотрим очень коротко,
подразделяется на сухое и вязкое (жидкое).
Применительно к сухому трению различают трение
скольжения, трение покоя и трение качения (подробно не будем
рассматривать).
Оказывается, что сила трения скольжения не зависит от площади
соприкосновения трущихся тел и пропорциональна величине силы
нормального давления (нормальной реакции поверхностей),
прижимающей трущиеся поверхности друг к другу:
Fтр(ск) N
(2.4)
Безразмерный коэффициент
называется коэффициентом
трения. Он зависит от природы и состояния трущихся поверхностей
и, в частности от их шероховатости.
PS. Коэффициент трения может зависеть также от относительной
скорости тел, которой обычно пренебрегают.

5.

Пример 1. Рассмотрим брусок, покоящийся на наклонной доске
(рис. 2.9). Условие равновесия бруска можно записать в виде
mg R 0
R
N
Fтр(п)
mg
Рис. 2.9
Если расположить доску горизонтально, поставить на нее
брусок, а затем медленно поднимать левый конец доски,
увеличивая угол наклона к горизонту, то произойдет, очевидно,
следующее. Вначале брусок относительно доски не движется.
При этом выполняется условие равновесия, откуда следует :
Fтр(п) mg sin

6.

– и так – вплоть до некоторого max , при котором начинается
медленное соскальзывание. При медленном соскальзывании
можно считать ускорение бруска пренебрежимо малым, и тогда
силу трения, являющуюся силой трения скольжения, можно
вычислить по формуле:
Fтр(ск) m gcos
Это позволяют сделать вывод, что сила трения покоя,
возникающая при попытке сдвинуть тело относительно
поверхности другого тела, с которым оно находится в контакте,
подчинена неравенству
0 Fтр(п) Fтр(ск)
Таким образом, ограничение сверху на силу трения покоя имеет
вид:
( п)
тр
F
N

7.

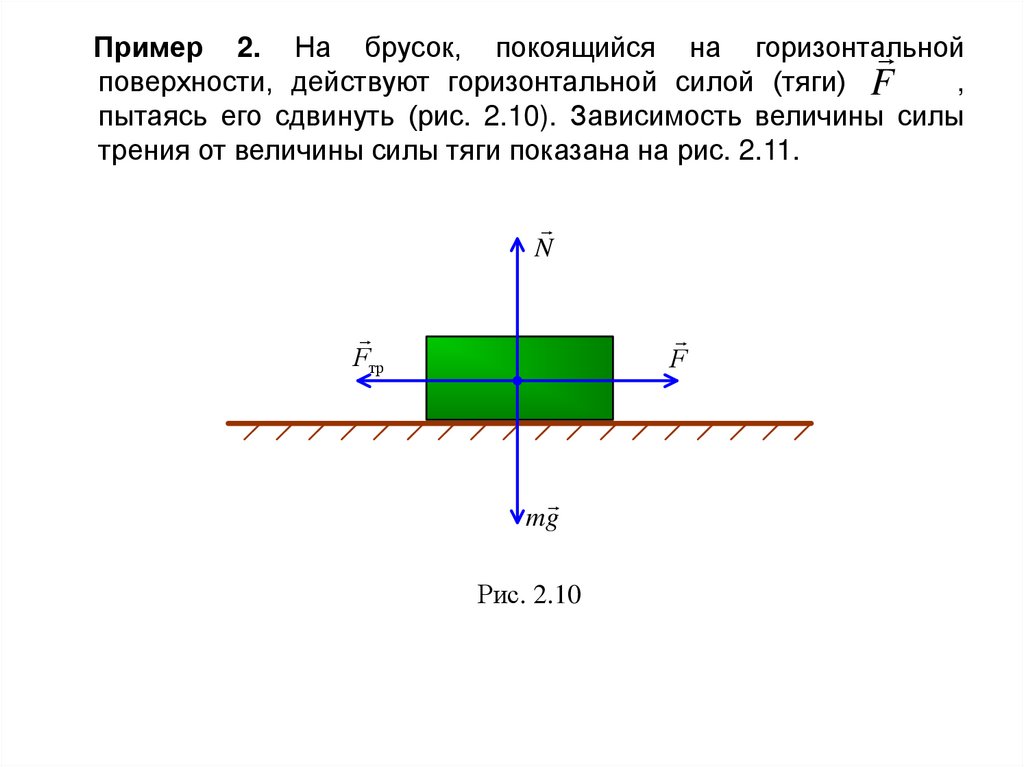
Пример 2. На брусок, покоящийся на горизонтальной
поверхности, действуют горизонтальной силой (тяги) F
,
пытаясь его сдвинуть (рис. 2.10). Зависимость величины силы
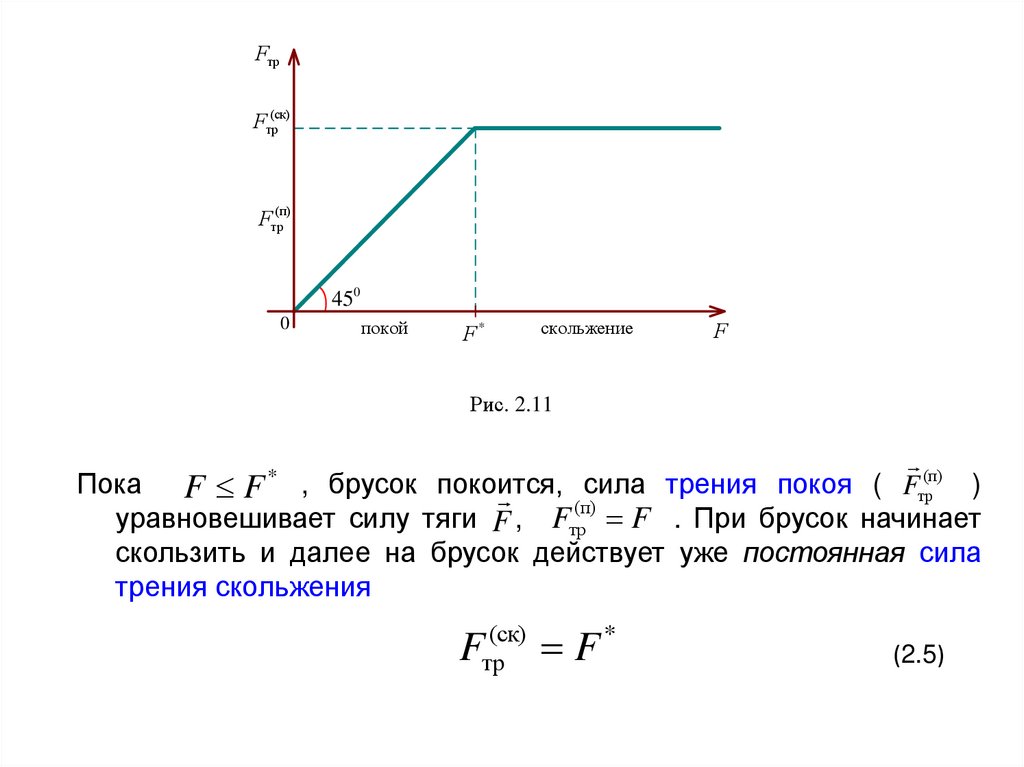
трения от величины силы тяги показана на рис. 2.11.
N
Fтр
F
mg
Рис. 2.10

8.

Fтр
Fтр(ск)
Fтр(п)
450
0
покой
F*
скольжение
F
Рис. 2.11
(п)
Пока F F , брусок покоится,
сила трения покоя ( Fтр )
(п)
уравновешивает силу тяги F , Fтр F . При брусок начинает
скользить и далее на брусок действует уже постоянная сила
трения скольжения
*
Fтр(ск) F *
(2.5)

9.

Закон всемирного тяготения. Гравитационное поле.
2.4.
В выражении для силы гравитационного взаимодействия (2.7) ,
так называемые, гравитационные массы совпадают с известными
нам инертными массами материальных точек.
Гравитационная постоянная:
G 6,67 10 11 Н.м2/кг2
m1m2 r12
F2,1 G 2
r
r
(2.7)
m2
r12
mm
Fгр G 1 2 2
r
r
r r12
m1
Рис. 2.17

10.

Введем определение.
Свободным падением материальной точки (тела) называется ее
движение под действием одной лишь силы тяжести
g
(гравитационной силы). Ускорение свободного падения
.
Пример 1. Рассмотрим планету радиуса R и массы M и будем
считать распределение массы по ее объему центральносимметричным. Тогда на МТ m , находящуюся на расстоянии r
от центра планеты на высоте h над ее поверхностью,
действует сила тяжести
Mm
Mm
F G 2 G
r
( R h) 2
Ускорение свободного падения на высоте h
M
g ( h) G
( R h) 2
(2.8)

11.

У поверхности планеты ( h 0 )
M
g0 G 2
R
.
(2.9)
Из (2.8) и (2.9) следует
R
g ( h) g 0
R h
2
. (2.10)
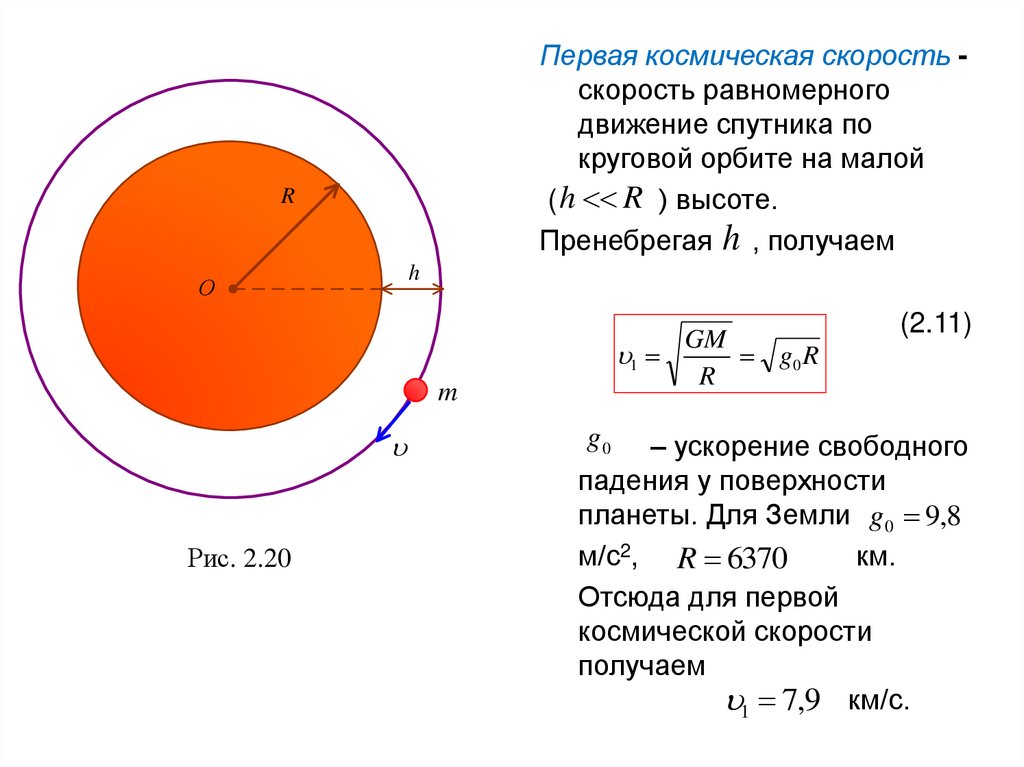
Пример 2. Пусть имеется спутник , движущийся вокруг планеты по
круговой орбите на высоте (рис. 2.20). Центростремительное
ускорение спутника совпадает с ускорением свободного
падения:
2
M
G
R h
( R h) 2
Отсюда скорость спутника
GM
R h

12.

Первая космическая скорость скорость равномерного
движение спутника по
круговой орбите на малой
( h R ) высоте.
Пренебрегая h , получаем
R
h
О
GM
1
g0 R
R
m
Рис. 2.20
g0
(2.11)
– ускорение свободного
падения у поверхности
планеты. Для Земли g0 9,8
м/с2, R 6370
км.
Отсюда для первой
космической скорости
получаем
1 7,9 км/с.

13.

2.5. Импульс материальной точки и механической системы.
Второй закон Ньютона в импульсной форме.
Импульсом материальной точки называется величина
p m
(2.12)
где m – масса м.т., – ее скорость (мгновенная).
Импульсом механической системы (набор материальных точек)
называется величина
P pi mi i
i
i
.
(2.13)
Продифференцируем по времени определение импульса:
dp
ma
dt
Таким образом, второй закон Ньютона в импульсной форме имеет вид
dp
F
dt
(2.14)

14.

Закон сохранения импульса.
Рассмотрим следствие уравнения движения (2.14):
( ex )
F 0 P const
.
(2.15)
т.е. если сумма внешних сил, действующих на систему, равна
нулю, то импульс системы сохраняется.
PS . Cитуации, когда можно
(ex ) гарантировать выполнение равенства
F 0,
являются достаточно редкими. Значительно шире класс таких
задач, в которых внешними силами, действующими на систему,
можно пренебречь и рассматривать систему как замкнутую.
Традиционная формулировка закона сохранения гласит:
импульс замкнутой системы сохраняется.

15.

РАБОТА и МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
3.1. Работа силы.
Пусть на движущуюся материальную точку(МТ) действует постоянная
(не зависящая явно от времени) однородная (не зависящая от
координат МТ) сила F const
. За промежуток времени ( t1 , t2 ) МТ
совершает перемещение S (t1 , t 2 ) .
S
Работой силы F const на перемещении
называется
величина
где F , S
A F S
A F S cos
– угол между силой и перемещением.
A F r
Или
r S
(3.1)
Работа величина скалярная и обладает свойством аддитивности.
n
n
n
A Ai
S S i ri
Ai F Si F ri
i 1
i 1
i 1
Обобщим определение на случай неоднородного силового
поля, когда
F F (r )

16.

в
Fi
Qi
ri
L
а
Рис. 3.1
На рис.3.1 показан отрезок L траектории МТ.
Будем считать эти участки
настолько малыми, чтобы изменением силы F при движении в пределах
данного i-го участка можно пренебречь. Тогда
A lim
F
(
Q
)
r
i i
(3.2)
ri 0
i
Предел суммы в правой части (3.2) называется криволинейным интегралом
вдоль кривой L между точками а и в
A F (r )dr
L
Это и есть определение работы неоднородной силы.
(3.3)

17.

3.2. Кинетическая энергия системы. Теорема о кинетической
энергии.
Кинетической энергией МТ называется величина
m 2
k
,
(3.4)
2
где m – масса, – модуль скорости материальной точки; [k] = Дж.
Кинетической энергией механической системы (набор материальных точек)
называется величина
K ki
(3.5)
i
где ki – кинетическая энергия i-й материальной точки; i=1, 2,…, n.
Существует связь между изменением кинетической энергии материальной
точки за некоторый промежуток времени ( t1 , t2) и работой действующих на
нее при этом сил.
k (t1, t2 ) A(t1, t2 )
(3.6)
Равенство теорема о кинетической энергии для МТ: изменение
кинетической энергии за некоторый промежуток времени равно сумме
работ действующих на МТ сил (совершенных за это время).
Для системы:
(3.7)
K (t1 , t 2 ) A (t1 , t 2 )
т.е. изменение кинетической энергии механической системы равно сумме
работ всех сил (внешних и внутренних), действующих на систему.

18.

3.3. Консервативные и неконсервативные силы.
Потенциальная энергия.
Пусть в некоторой области (или во всем пространстве)
существует статическое
силовое поле: на МТ в этой области
действует сила F , в общем
случае зависящая от положения
материальной
F F (r )
точки:
Сила F F (r ) называется консервативной, если работа силы
над материальной точкой при ее перемещении из точки а в точку в
не зависит от формы отрезка траектории , соединяющего а и в, а
определяется только начальным (а) и конечным (в) положениями
материальной точки:
AF (a в) A(rа , rв )
Работа консервативной силы:
в
F
(
r
)
d
r
F
(
r
)
d
r
A
(
r
а , rв )
L1
L1
L2
Очевидно, что
F (r )dr
L1 ( в а )
L2
т.е.
F (r )dr 0
F ( r ) dr
L1 ( а в )
L
F F (r )
а
Рис. 3.3
Сила
называется консервативной,
если ее работа над МТ на любом замкнутом
контуре равна нулю.

19.

P.S. Интеграл F (r )dr 0 называется циркуляцией вектора F по
L
замкнутому контуру L .
Таким образом, если сила
то существует такая
F (r ) консервативна,
скалярная физическая величина
, убыль которой при
П П( r )
перемещении а в МТ равна работе консервативной силы на этом
перемещении:
Aконс (а в) П( rа ) П( rв )
Величина П П( r ) называется потенциальной энергией МТ.
Очевидно, что потенциальная энергия определена неоднозначно, с
точностью до некоторой постоянной. Обычно, чтобы избавиться от этой
неоднозначности, указывают точку, где потенциальная энергия
принимается равной нулю. Тогда потенциальная энергия становится
однозначной функцией координат и приобретает физический смысл:
Потенциальная энергия численно равна работе консервативной силы
при переходе материальной точки из выбранного положения в точку,
где потенциальная энергия принята равной нулю.
(3.8)
Aконс П
Aконс dП
Для бесконечно малых величин имеем соответственно:
т.е. определение потенциальной энергии в дифференциальной форме.

20.

Тогда, используя связь работы и потенциальной энергии имеем:
(3.9)
dП Fdr
Более общее выражение связи силы и потенциальной энергии
(3.10)
П П П
F grad П
grad П
x
В декартовых координатах проекции:
i
y
Fx
j
П
x
z
k
Fy
П
y
Fz
П
z
Это уравнение используется при построении выражений для
потенциальной энергии МТ в консервативных силовых полях.
Определение.
Силы, не
являющиеся консервативными,
называются неконсервативными силами.
Примеры.
Консервативные силы: сила тяжести, сила упругости,
квазиупругая сила, кулоновская сила.
Неконсервативные силы: все виды сил трения, сила
Лоренца.
Далее,
используя
(3.10)
вычислим
соответствующие
потенциальные энергии.

21.

Примеры постоянных однородных сил.
1. Сила тяжести.
П2 mg r
Для силы тяжести, направив ось OY вверх, будем иметь:
,
g r g x x g y y g z z ( g ) y
т.е. получаем хорошо известное выражение
F2 mg
(3.11)
(3.12)
П2 П2 ( y) mgy
2. Сила упругости.
Пусть движение МТ ограничено
осью OX и пусть Fx Fx (x) .
Тогда
A Fdr Fx ( x)dx
и потенциальная энергия оказывается функцией координаты материальной
точки: П П( x) ,
Для упругой силы:
dП( x) Fx ( x)dx
П( x) Fx ( x)dx
при условии
Fx ' kx
выражение для потенциальной энергии:
kx2
П 3 ( x)
2
П3 (0) 0
(3.13)

22.

m2
r
r
3. Гравитационное поле. На материальную точку
m2 со стороны МТ m1 , которую мы считаем
покоящейся в начале отсчета О (рис. 3.4), действует
гравитационная сила.
(3.14)
m1m2 r
F G
m1
r
2
r
В скалярной форме f (r ) сила выражается равенством
О
f (r ) G
Рис. 3.4
m1 m2
r2
Потенциальная энергия МТ m2 в поле, создаваемом материальной точкой m1 :
mm
П( r ) G 1 2 2 dr
r
lim П( r ) 0
При дополнительном (вполне естественном) условии:
Получаем
П 4 (r ) G
m1m2
r
r
(3.15)
Выражение (3.15) симметрично относительно индексов 1 и 2, т.е. если бы мы
m2 , то
вычисляли потенциальную энергию m1 в поле неподвижной точки
получили бы также результат. Поэтому (3.15) называется потенциальной
энергией гравитационного взаимодействия двух материальных точек.

23.

3.4. Механическая энергия системы. Теорема об изменении
механической энергии. Закон сохранения механической энергии.
Механической энергией системы называется сумма ее кинетической и
потенциальной энергий:
E K П .
(3.16)
Изменение механической энергии за некоторый промежуток времени:
.
E K П
Имея в виду, что силы делятся на консервативные и неконсервативные,
запишем сумму работ всех сил над системой в виде суммы двух слагаемых:
(3.17)
А Анек Аконс .
Используя теорему о кинетической энергии, перепишем (3.16) в виде
Е Анек Аконс П .
(3.18)
Из определения потенциальной энергии следует, что последние два слагаемых
в правой части (3.18) в сумме дают ноль. Поэтому
Е Анек ,
(3.19)
т.е. изменение механической энергии системы за некоторый промежуток
времени равно сумме работ неконсервативных сил, действующих в системе,
совершенных за это время (теорема об изменении механической энергии).
Из (3.19) следует закон сохранения механической энергии: если сумма
работ неконсервативных сил, действующих в замкнутой системе, равна нулю,
то механическая энергия системы сохраняется.

24.

Традиционная формулировка закона сохранения механической энергии: если все
силы, действующие в замкнутой механической системе, консервативны, то
механическая энергия системы сохраняется.
Пример. Используя закон сохранения механической энергии, найдем вторую
космическую скорость: это минимальная скорость, которую надо сообщить телу
у поверхности Земли (или другой планеты) для того, чтобы оно могло удалиться
от Земли на бесконечно большое расстояние.
Mm
Потенциальная энергия тела в гравитационном поле:
П G
r
где m – масса
тела, M – масса Земли, r – расстояние между телом и центром
Земли, r – радиус-вектор тела, проведенный из центра планеты. Закон
0 - скорость на поверхности планеты):
сохранения имеет вид (
m 02
Mm m 2
Mm
G
G
2
R
2
r
Полагая на бесконечно большом
r расстоянии:
M
2 g0 R
R
Подставляя в (3.) параметры Земли g0 9,8 м/с2,
2 0 min 2G
2 11,2
км/с.
0 , имеем:
(3.20)
R 6,37 106
м, получаем

25.

3.5 Законы сохранения
как следствия симметрии пространства и времени
1. Понятие симметрии в естествознании:
инвариантность относительно тех или иных преобразований.
2. Простейшие симметрии: однородность (одинаковые свойства во всех
точках) и изотропность (одинаковые свойства во всех направлениях).
Симметрии пространства и времени:
- однородность и изотропность пространства
- однородность времени (время необратимо, т.е. анизотропно).
Теорема Нётер (теоретическая физика) утверждает, что каждой
непрерывной симметрии соответствует некоторый закон сохранения.
Фундаментальность законов сохранения заключается в их
универсальности. Они справедливы при изучении любых физических
процессов (механических, тепловых, электромагнитных и др.).
Они одинаково применимы в релятивистском и нерелятивистском
движении, в микромире, где справедливы квантовые представления, и в
макромире, с его классическими представлениями.

26.

1) Закон сохранения энергии - следствие однородности времени. т. е.
равнозначность всех моментов времени (симметрия по отношению к
сдвигу начала отсчета времени).
Равнозначность следует понимать в том смысле, что замена момента
времени t1 на момент времени t2, без изменения значений координат и
скорости частиц, не изменяет механические свойства системы. Это
означает то, что после указанной замены, координаты и скорости частиц
имеют в любой момент времени t2 + t такие же значения, какие имели до
замены, в момент времени t1 + t.
2) Закон сохранения импульса - следствие однородности пространства.
т. е. одинаковость свойств пространства во всех точках (симметрия по
отношению к сдвигу начала координат).
Одинаковость следует понимать в том смысле, что параллельный перенос
замкнутой системы из одного места пространства в другое, без изменения
взаимного расположения и скоростей частиц, не изменяет механические
свойства системы.
3) Закон сохранения момента импульса (вращательное движение) следствие изотропности пространства, т. е. одинаковость свойств
пространства по всем направлениям (симметрия по отношению к повороту
осей координат).
Одинаковость следует
понимать в
том смысле,
что
поворот
замкнутой системы, как целого, не отражается на её
механических
свойствах.

27.

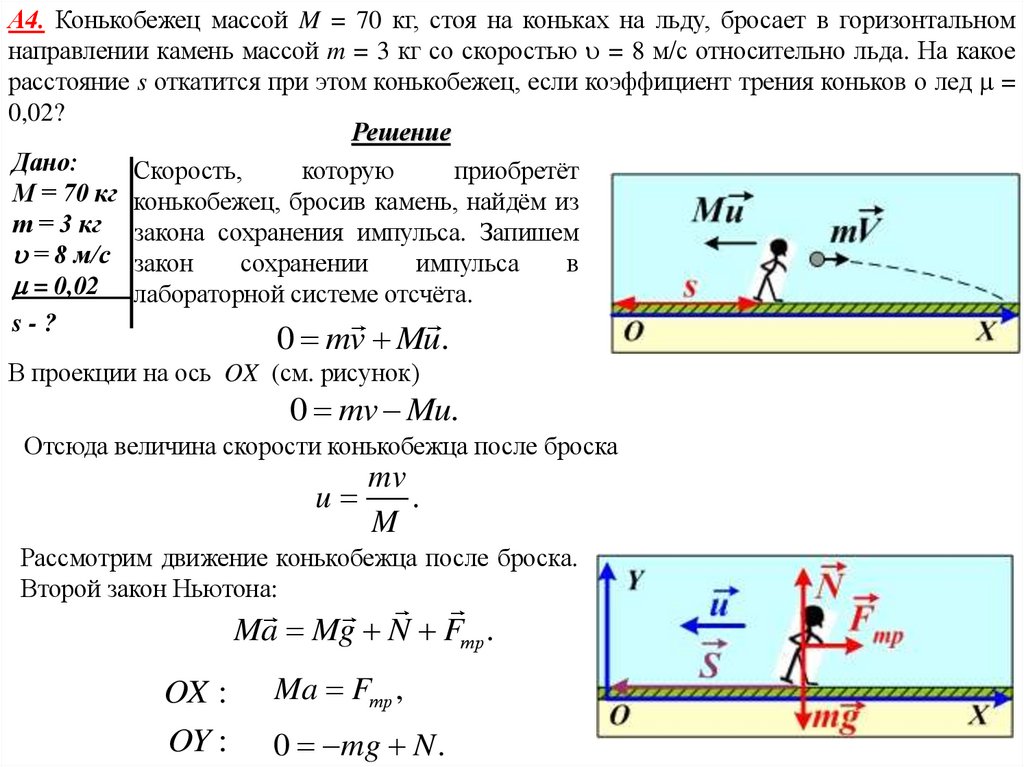
А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном
направлении камень массой m = 3 кг со скоростью = 8 м/с относительно льда. На какое
расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед =
0,02?
Решение
Дано:
Скорость,
которую
приобретёт
M = 70 кг конькобежец, бросив камень, найдём из
m = 3 кг закона сохранения импульса. Запишем
= 8 м/с закон
сохранении
импульса
в
= 0,02 лабораторной системе отсчёта.
s-?
0 mv Mu.
В проекции на ось OX (см. рисунок)
0 mv Mu.
Отсюда величина скорости конькобежца после броска
mv
u
.
M
Рассмотрим движение конькобежца после броска.
Второй закон Ньютона:
Ma Mg N Fтр .
OX :
OY :
Ma Fтр ,
0 mg N .

28.

А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном
направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s
откатится при этом конькобежец, если коэффициент трения коньков о лед = 0,02?
Решение (продолжение)
OX :
OY :
ma Fтр ,
0 Mg N .
Величина силы трения скольжения
Fтр N .
N Mg ,
Fтр Mg .
Изменение полной механической энергии конькобежца равно работе неконсервативных
сил, то есть работе силы трения.
U 0,
Ek Aтр .
E Ek U ,
Mv22 Mv12
Mu 2
Mu 2
Ek
0
.
2
2
2
2
,
Aтр Fтр S cos MgS .
Aтр Fтр S cos ,
E Aтр ,

29.

А4. Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном
направлении камень массой m = 3 кг со скоростью = 8 м/с. На какое расстояние s
откатится при этом конькобежец, если коэффициент трения коньков о лед = 0,02?
Решение (продолжение)
Mu 2
Ek
,
2
Aтр MgS ,
E Aтр ,
Mu 2
MgS .
2
Отсюда
u 2 2 gS ,
u2
S
.
2 g
Подставим в последнюю формулу найденное ранее выражение для скорости
конькобежца u:
mv
u
,
M
u2
m2 v 2
S
2
.
2 g M 2 g
m2 v 2
32
82
S 2
2
0,3 м .
M 2 g 70 2 0,02 9,8
Ответ: S = 0,3

30.

№1. Движущийся по бильярдному столу шар
сталкивается с неподвижным шаром. Массы и
размеры шаров одинаковы. Считая удар упругим,
определить под каким углом будут двигаться
шары после столкновения.
Ответ.
1) 0;
2)