Прямоугольный параллелепипед

1.

11.02.25
Классная работа
Прямоугольный параллелепипед
Глава 2, § 3, п. 24.

2.

Изучение нового материала

3.

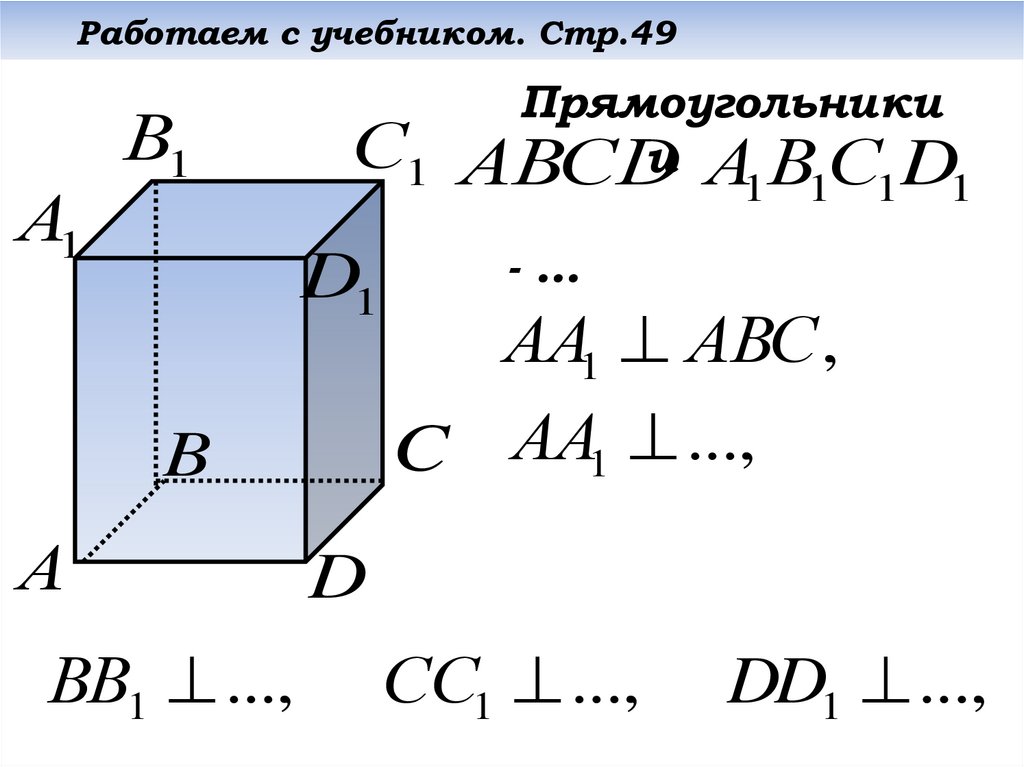
Работаем с учебником. Стр.49
Заполните пропуски.
1. Параллелепипед называется
прямоугольным, если его боковые
ребра перпендикулярны к
основаниям, а основания
представляют собой прямоугольники

4.

Работаем с учебником. Стр.49
А1
В1
Прямоугольники
С1 АВСD
и АВС D
1
D1
B
А
ВВ1 ...,
1
1
1
-…
АА1 АВС ,
C АА1 ...,
D
СС1 ...,
DD1 ...,

5.

Работаем с учебником. Стр.49
А1
В1
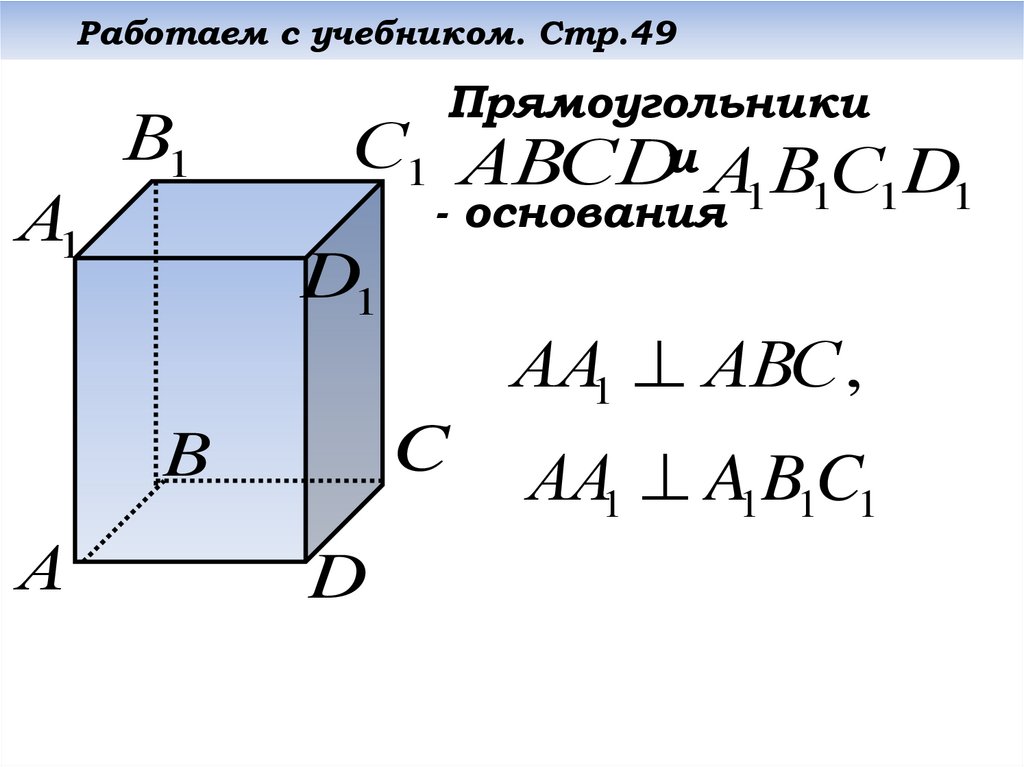
Прямоугольники
С1 АВСDи А В С D
1
1
1
1
- основания
D1
C
B
А
АА1 АВС ,
D
АА1 A1B1C1

6.

Работаем с учебником. Стр.49
А1
В1
С1
D1
прямоугольного
параллелепипеда:
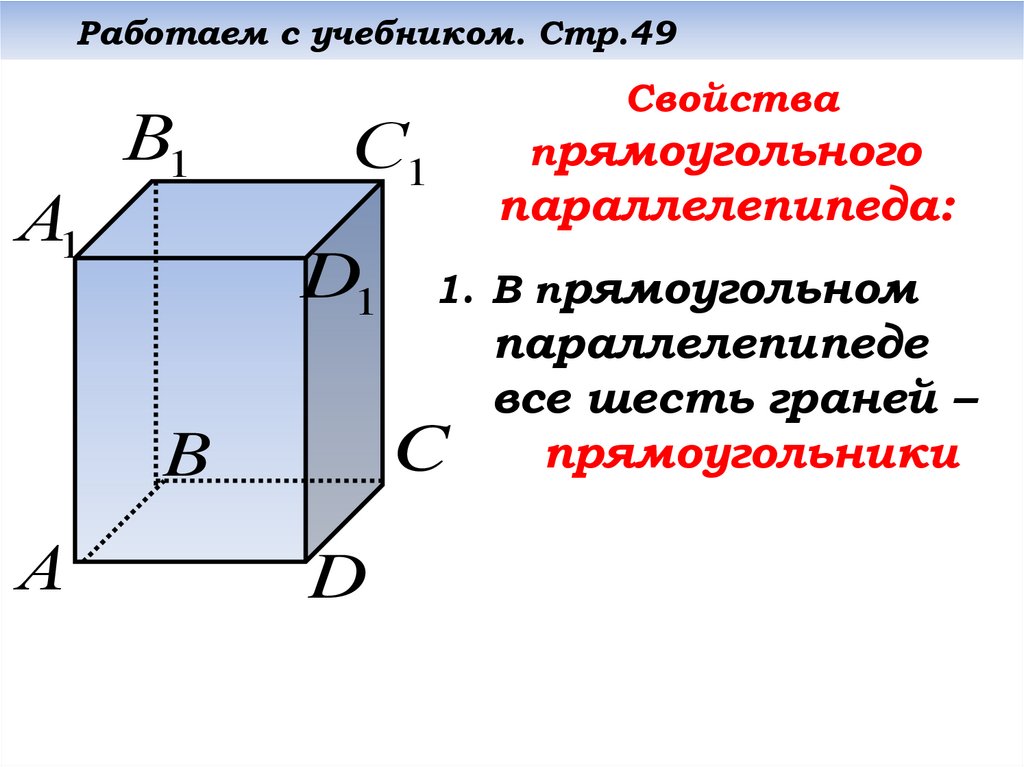
1. В прямоугольном
C
B
А
Свойства
D
параллелепипеде
все шесть граней –
прямоугольники

7.

Работаем с учебником. Стр.49
А1
В1
С1
D1
B
А
C
D
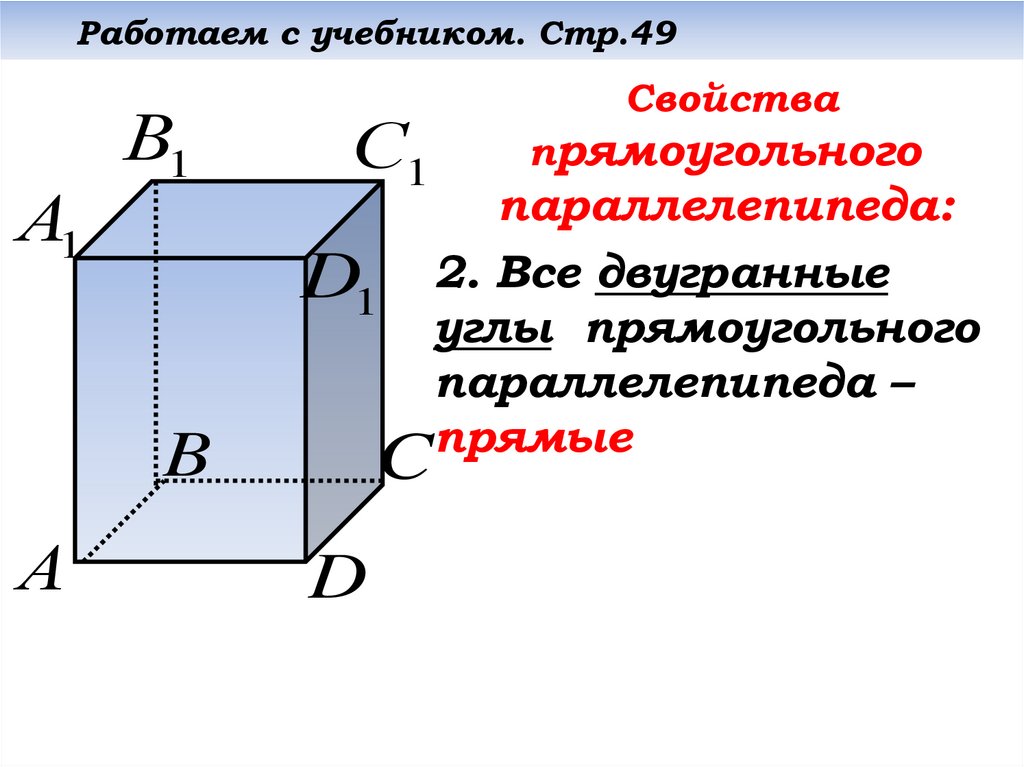
Свойства
прямоугольного
параллелепипеда:
2. Все двугранные
углы прямоугольного
параллелепипеда –
прямые

8.

Работаем с учебником. Стр.49
А1
В1
D1
B
А
С1
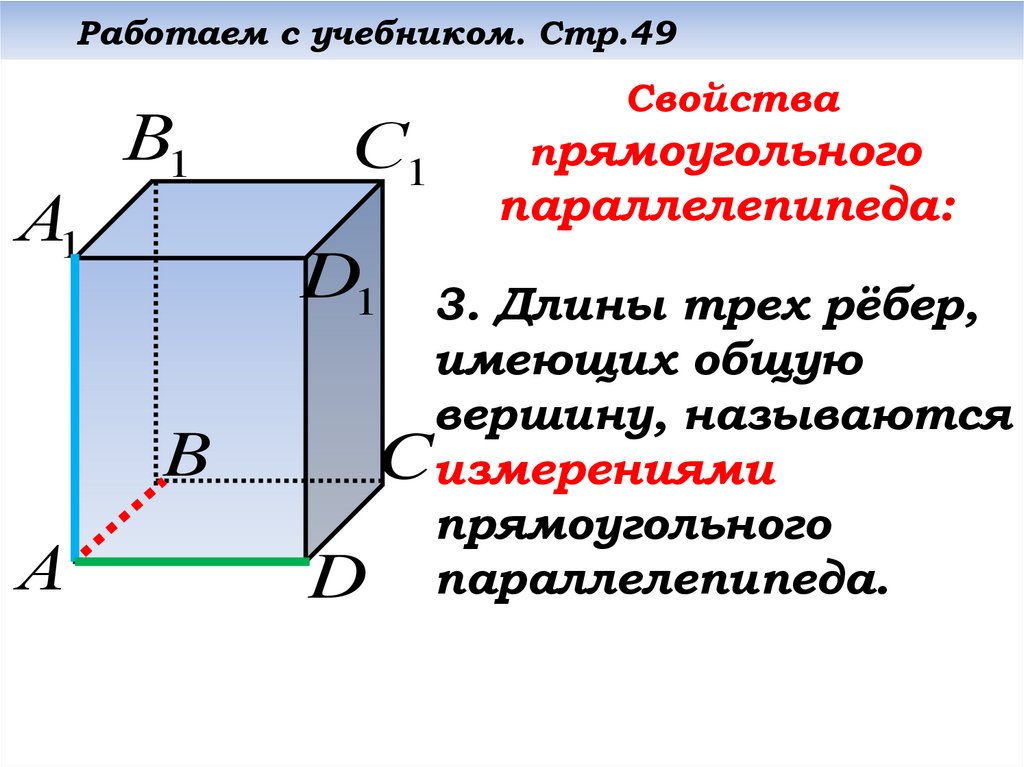
Свойства
прямоугольного
параллелепипеда:
3. Длины трех рёбер,
имеющих общую
вершину, называются
Cизмерениями
прямоугольного
D параллелепипеда.

9.

Работаем с учебником. Стр.49
А1
В1
B
А
С
D1 1
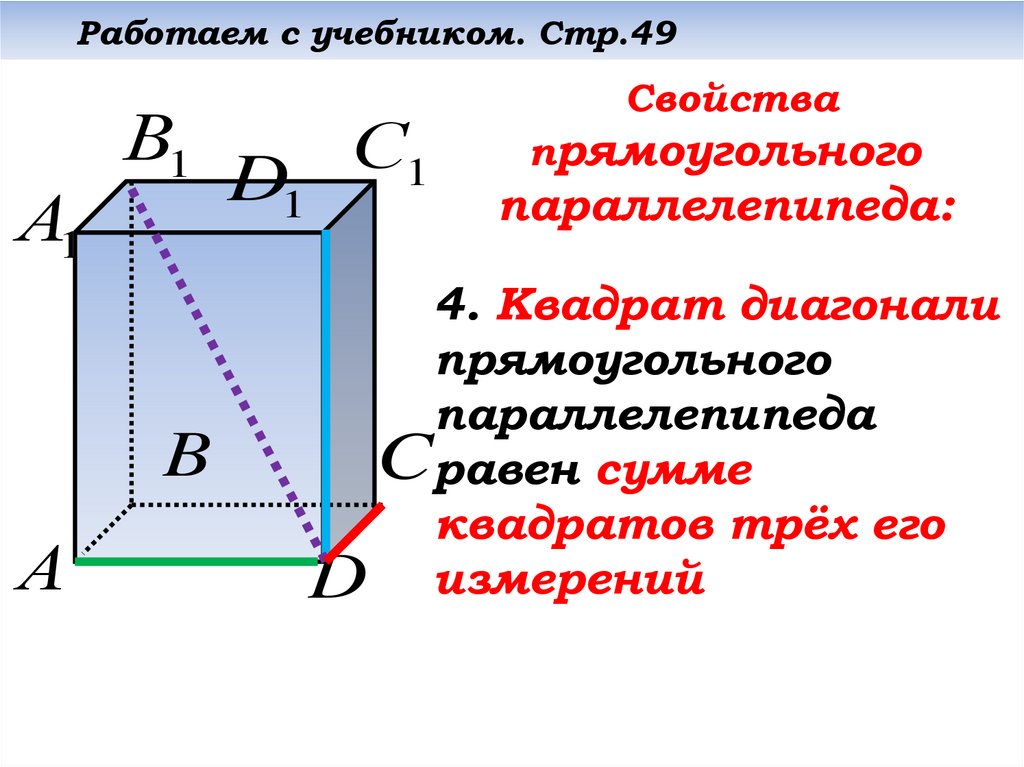
Свойства
прямоугольного
параллелепипеда:
4. Квадрат диагонали
прямоугольного
параллелепипеда
Cравен сумме
квадратов трёх его
D измерений

10.

Работаем с учебником. Стр.49
А1
В1
D1
С1
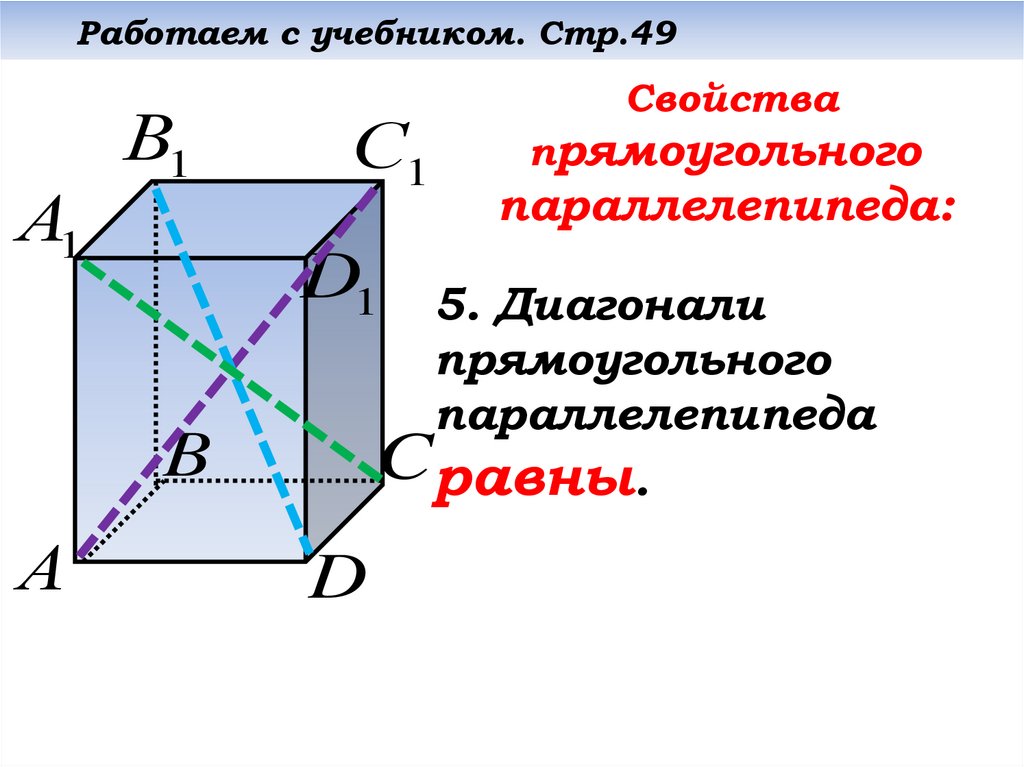
Свойства
прямоугольного
параллелепипеда:
4.* d
c
B
А
b
a
C
D
2
a b c
2
2
2

11.

Работаем с учебником. Стр.49
А1
В1
С1
D1
прямоугольного
параллелепипеда:
5. Диагонали
прямоугольного
параллелепипеда
Cравны.
B
А
Свойства
D

12.

Работаем с учебником. Стр.49
А1В1С1D1
АВСD
В1
А1
С1
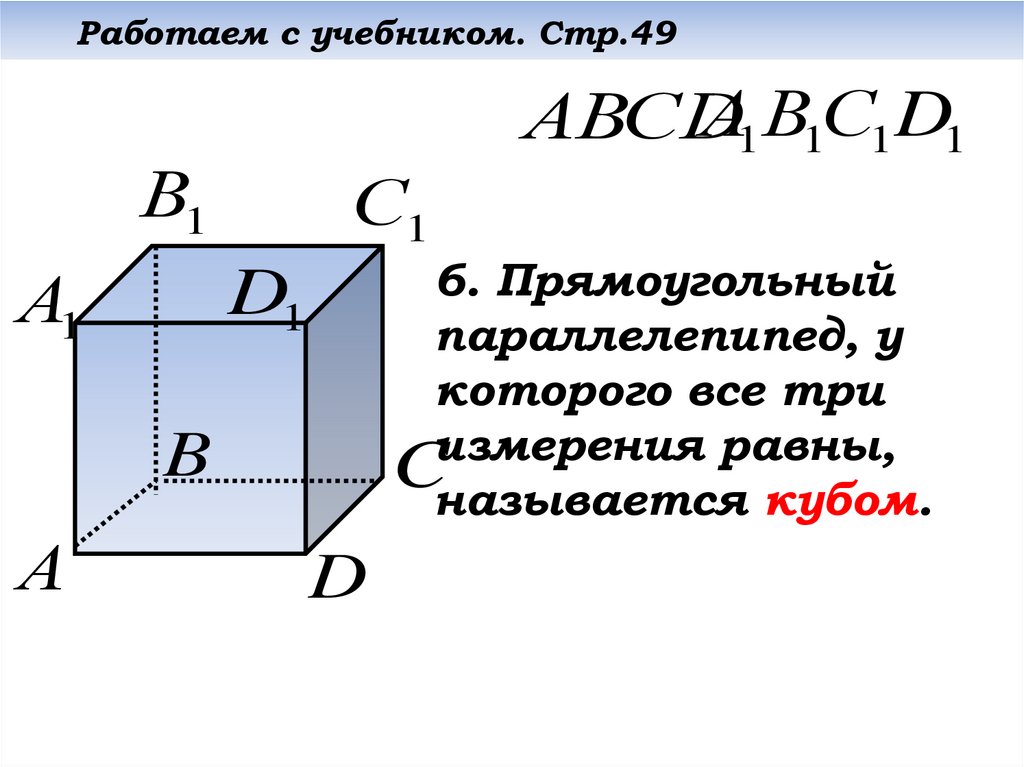
6. Прямоугольный
параллелепипед, у
которого все три
измерения равны,
Cназывается кубом.
D1
B
А
D

13.

Решаем задачи. Стр.56, №187
Выполните все задания

14.

Решаем задачи. Стр.56, №187
d a b c
2
2
2
а)d 1 1 2
2
2
2
2
2

15.

Решаем задачи. Стр.56, №187
d a b c
2
2
2
2
а)d 1 1 2 6
d 6
2
2
2
2

16.

Решаем задачи. Стр.56, №187
d a b c
2
2
2
б )d 8 9 12
64 81 144 289
2
2
2
2
d 289 17
2

17.

Решаем задачи. Стр.56, №187
d a b c
2
2
2
2
в )d ( 39 ) 7 9
39 49 81 169
2
2
2
d 169 13
2

18.

Решаем задачи. Стр.56

19.

Решаем задачи. Стр.56.
d a а а
2
2
2
2

20.

Решаем задачи. Стр.56.
d 3a
2
2

21.

Решаем задачи. Стр.56.
d 3a
2
2
d a 3

22.

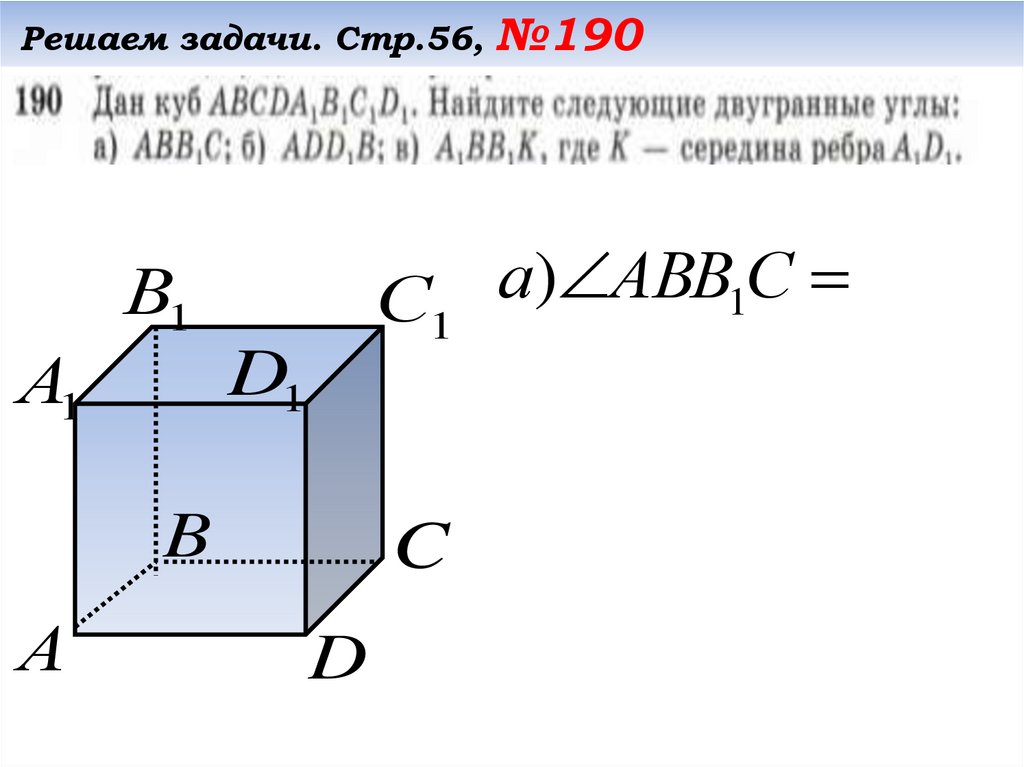
Решаем задачи. Стр.56, №190
а
)
АВВ
С
1
С1
В1
А1
D1
B
А
C
D

23.

Решаем задачи. Стр.56, №190
В1
А1
А
С1
D1
а ) АВВ1С 90 , т.к.
ВВ1 АВ, ВВ1 ВС ,
АВ ВС
C
B
D

24.

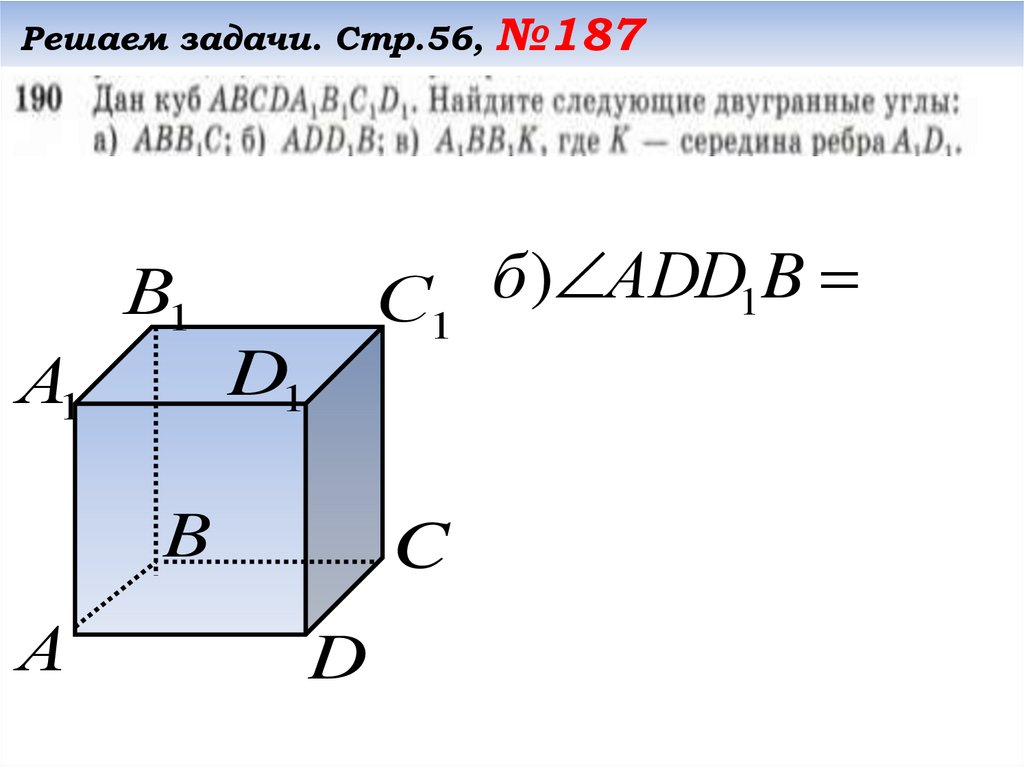
Решаем задачи. Стр.56, №187
б
)
АDD
B
1
С1
В1
А1
D1
B
А
C
D

25.

Решаем задачи. Стр.56, №187
В1
А1
С1
А
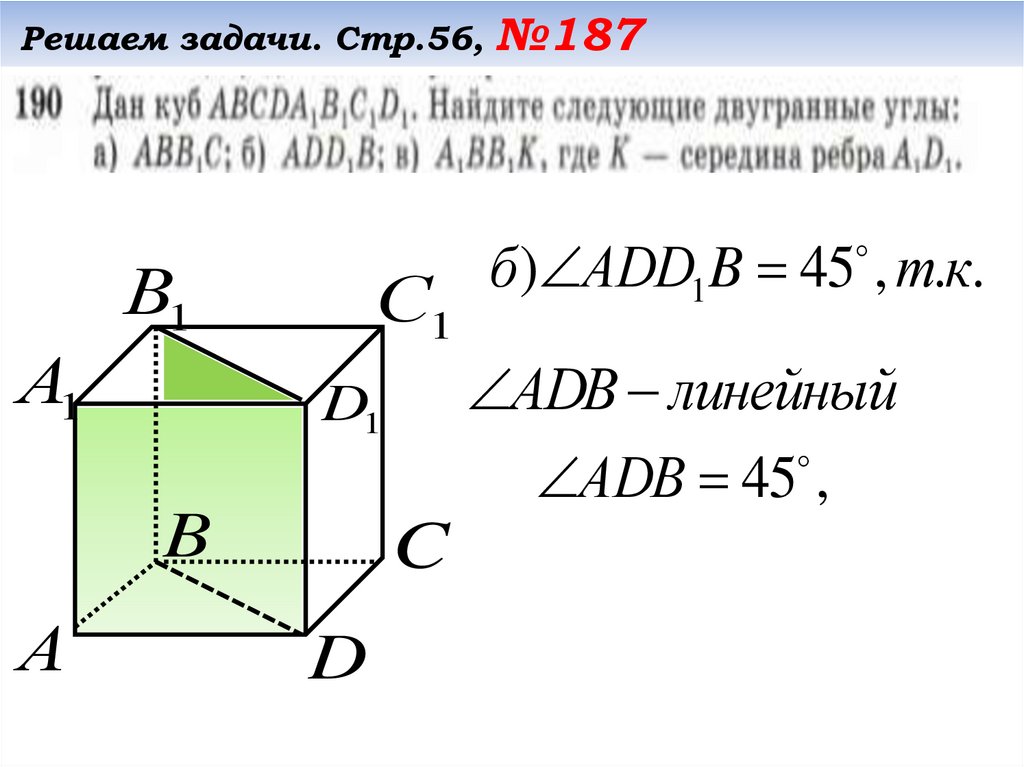
АDB линейный
АDB 45 ,
D1
B
C
D
б ) АDD1B 45 , т.к.

26.

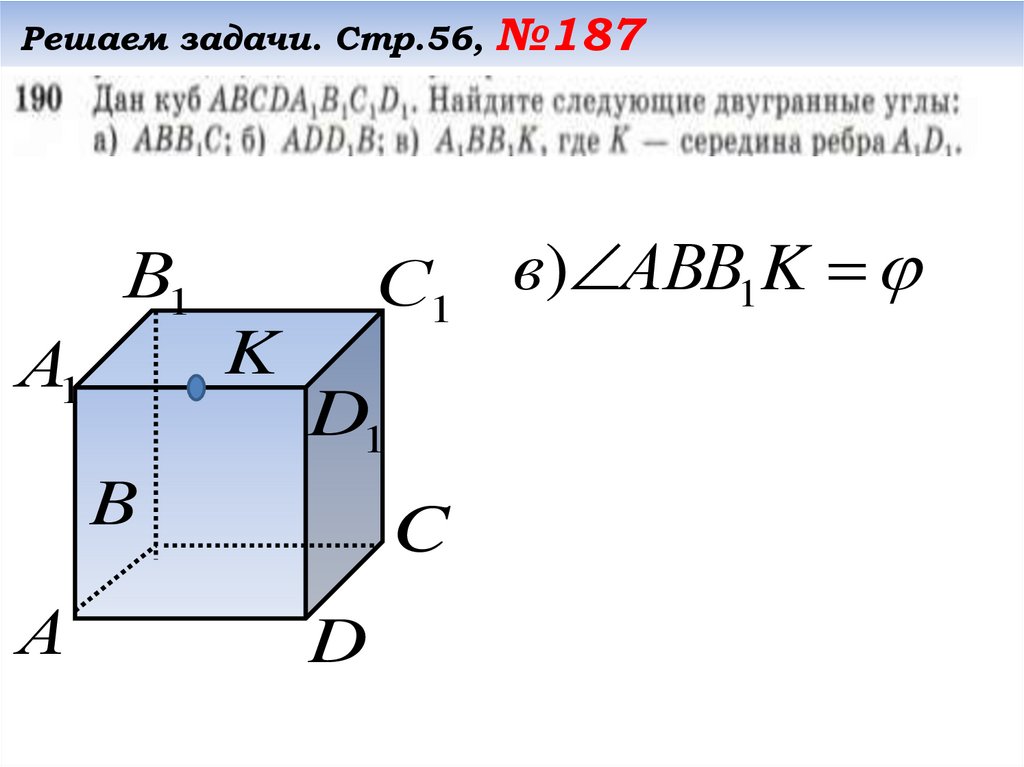
Решаем задачи. Стр.56, №187
С1 в) АBB1K
В1
А1
K
D1
B
А
C
D

27.

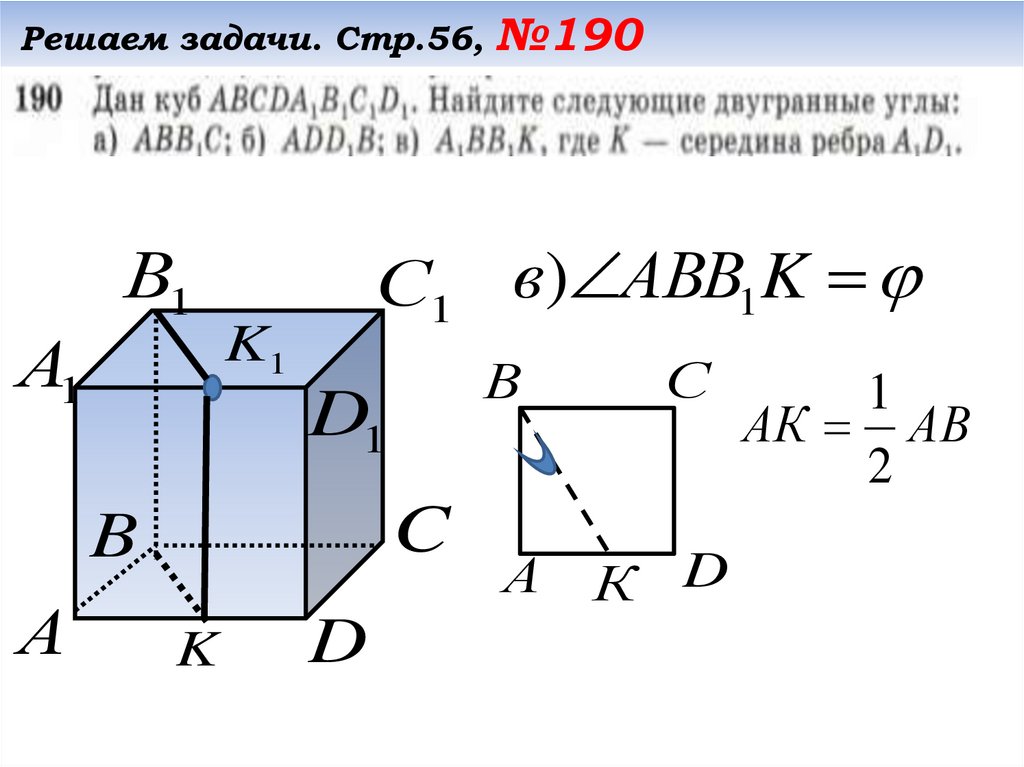
Решаем задачи. Стр.56, №190
С1 в) АBB1K
В1
K1
А1
D1
C
B
А
K
D
В
С
А
К D
1
АК АВ
2

28.

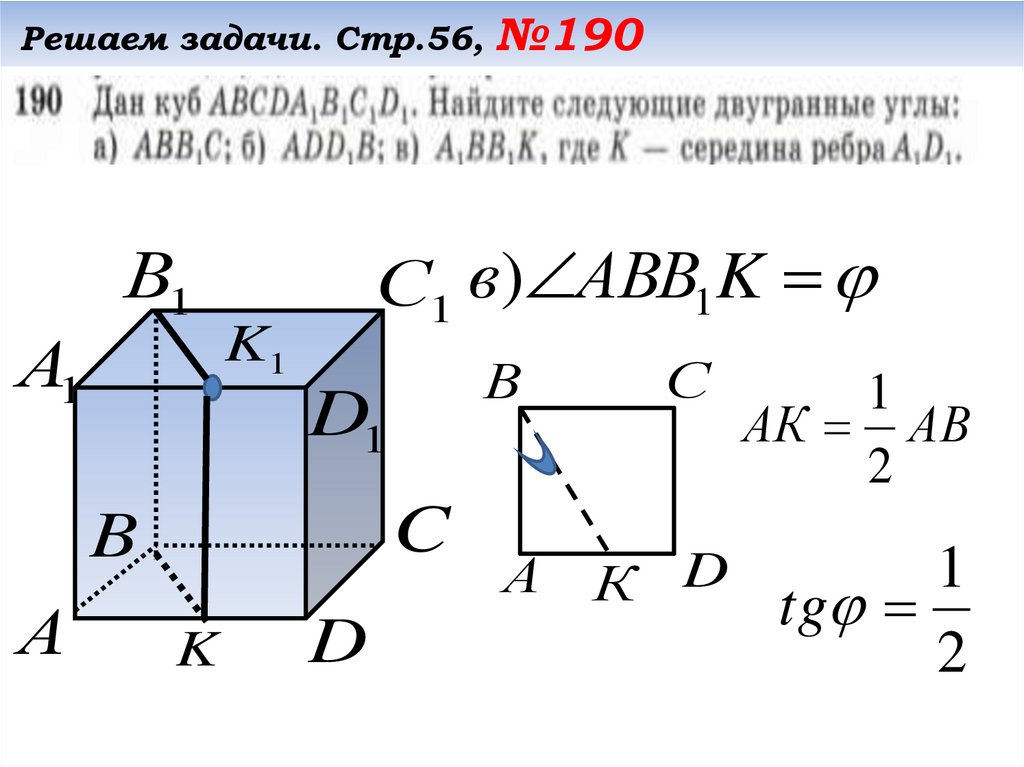
Решаем задачи. Стр.56, №190
С1 в) АBB1K
В1
K1
А1
D1
C
B
А
В
K
D
А
С
1
АК АВ
2
К D tg 1
2

29.

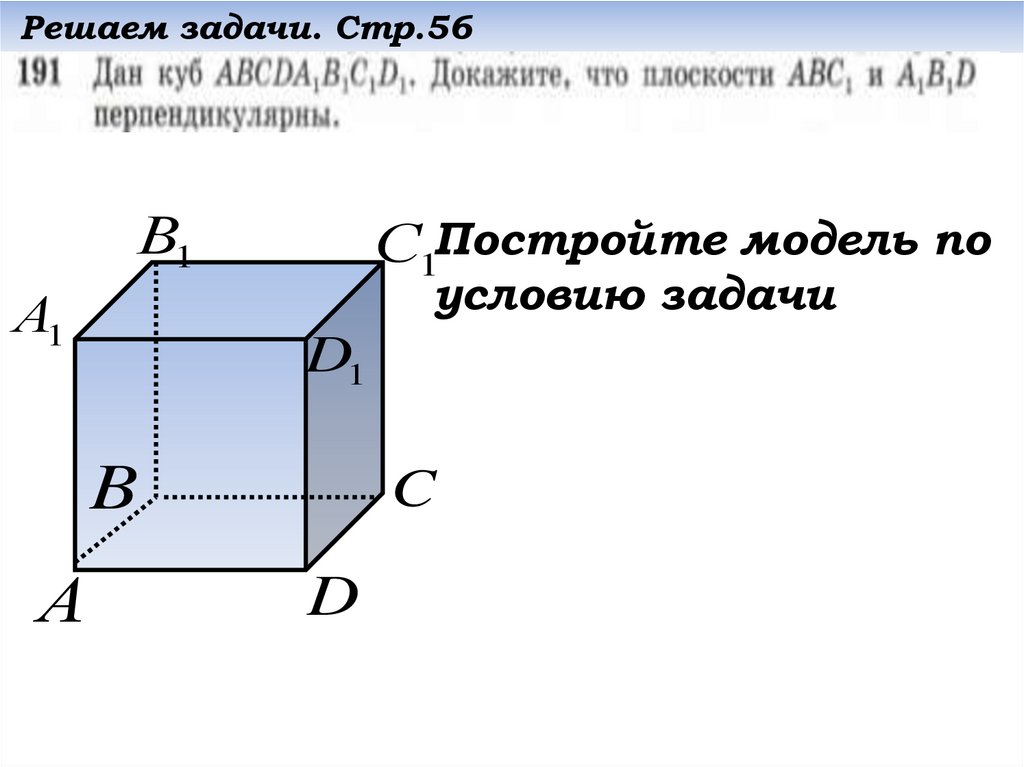
Решаем задачи. Стр.56
В1
А1
С1Постройте модель по
условию задачи
D1
B
А
C
D

30.

Решаем задачи. Стр.56
D1
А1
О1
D
А
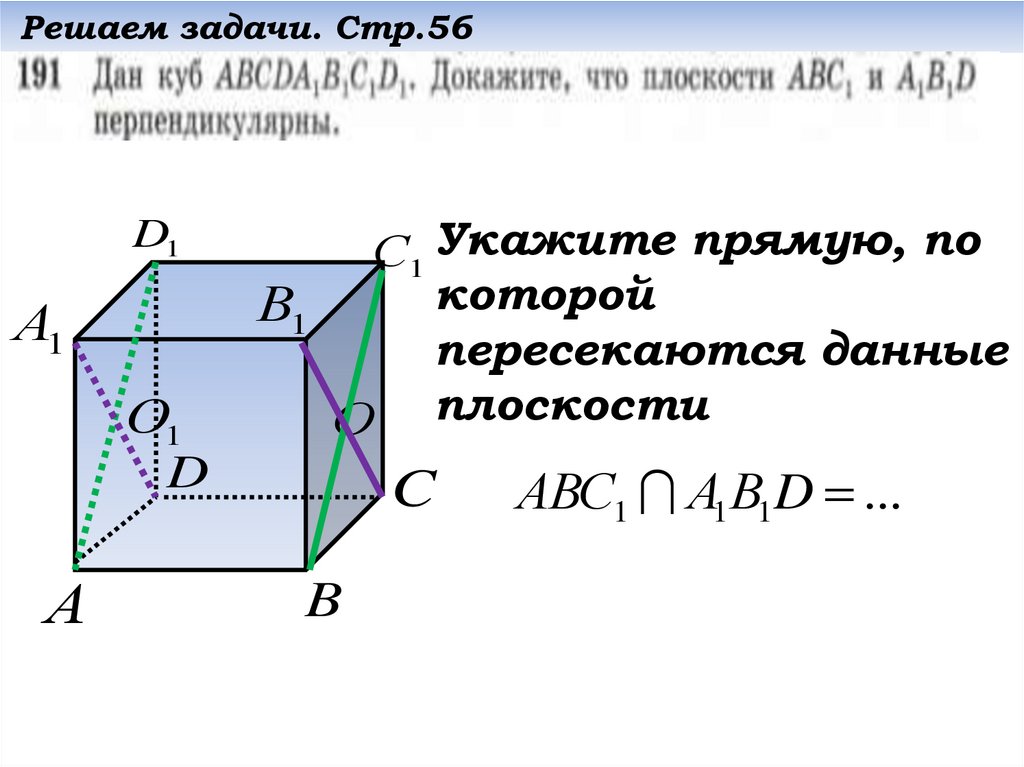
С1 Укажите прямую, по
которой
В1
пересекаются данные
О плоскости
C
B
АВС1 А1В1D ...

31.

Решаем задачи. Стр.56
D1
В1
А1
О1
D
А
С1
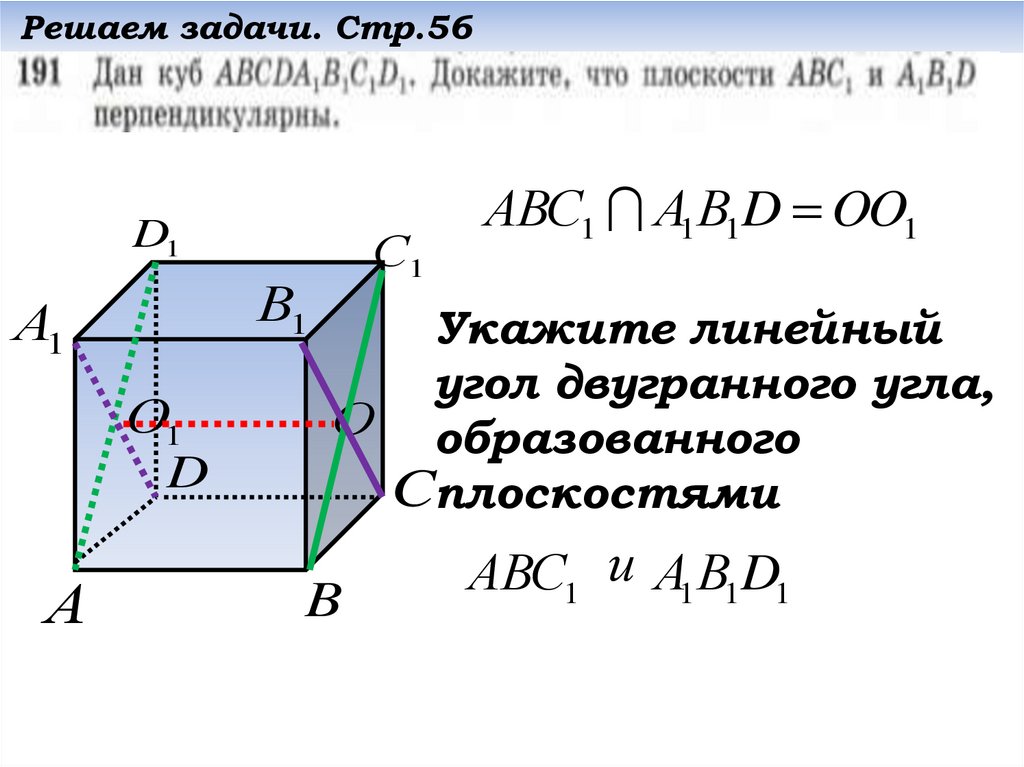
АВС1 А1В1D OO1
Укажите линейный
угол двугранного угла,
О образованного
Cплоскостями
B
АВС1 и А1В1D1

32.

Решаем задачи. Стр.56
D1
О1
D
А
С1
В1
А1
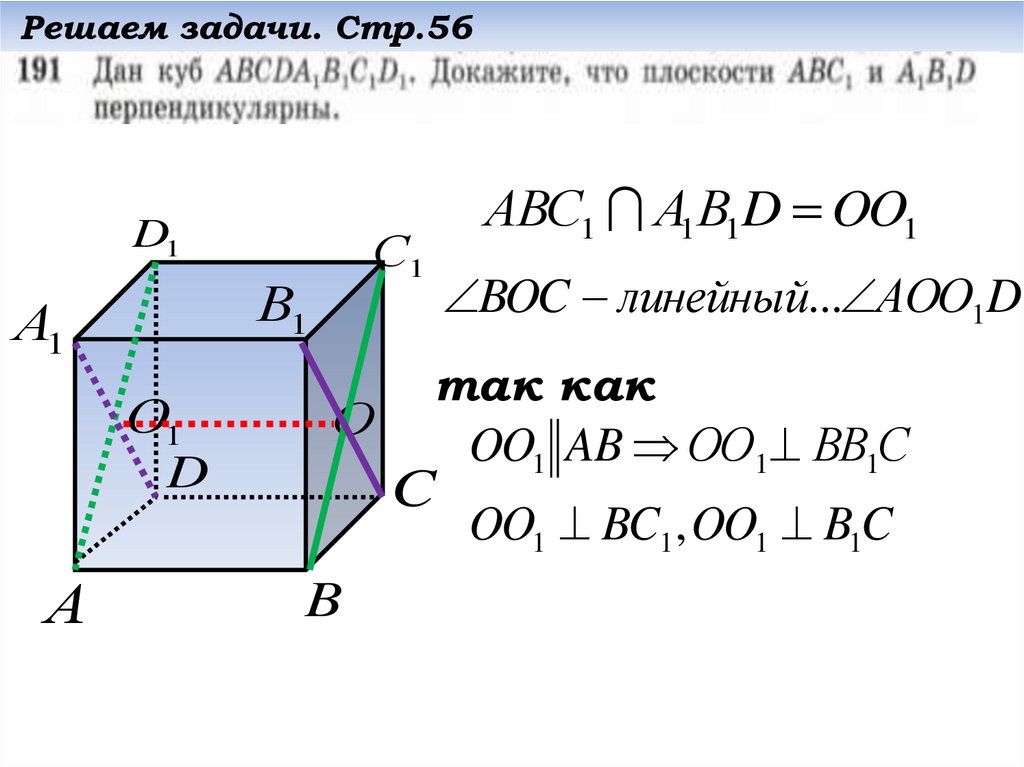
АВС1 А1В1D OO1
BOC линейный... АОО1D
О
так как …
C
B

33.

Решаем задачи. Стр.56
D1
О1
D
А
С1
В1
А1
АВС1 А1В1D OO1
О
BOC линейный... АОО1D
так как
C
B
OO1 AB ОО1 ВВ1С
OO1 BC1 , OO1 B1C

34.

Решаем задачи. Стр.56
D1
О1
D
А
С1
В1
А1
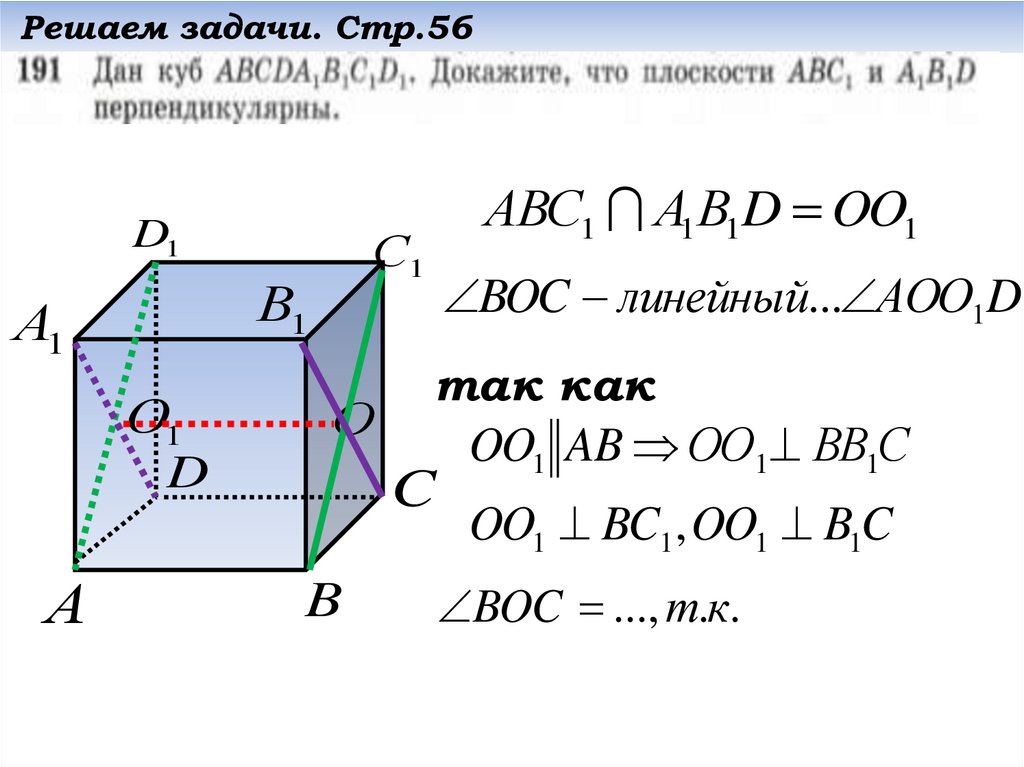
АВС1 А1В1D OO1
О
BOC линейный... АОО1D
так как
C
B
OO1 AB ОО1 ВВ1С
OO1 BC1 , OO1 B1C
BOC ..., т.к.

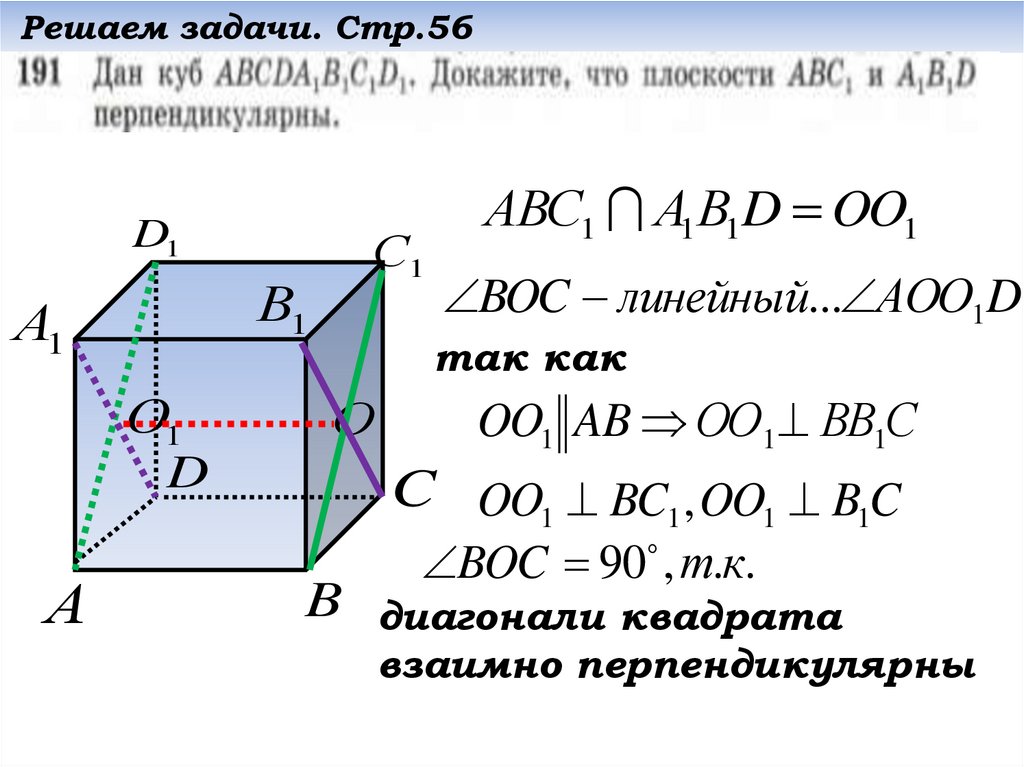
35.

Решаем задачи. Стр.56
D1
В1
А1
О1
D
С1
АВС1 А1В1D OO1
BOC линейный... АОО1D
так как
О
OO1 AB ОО1 ВВ1С
C OO1 BC1 , OO1 B1C
BOC 90 , т.к.
А
B диагонали квадрата
взаимно перпендикулярны

36.

Решаем задачи. Стр.56
АВС1 А1В1D OO1
D1
В1
А1
О1
D
А
С1
BOC линейный... АОО1D
так как
OO1 AB ОО1 ВВ1С
О
OO1 BC1 , OO1 B1C
C BOC 90 , т.к.
диагонали квадрата
взаимно перпендикулярны
B
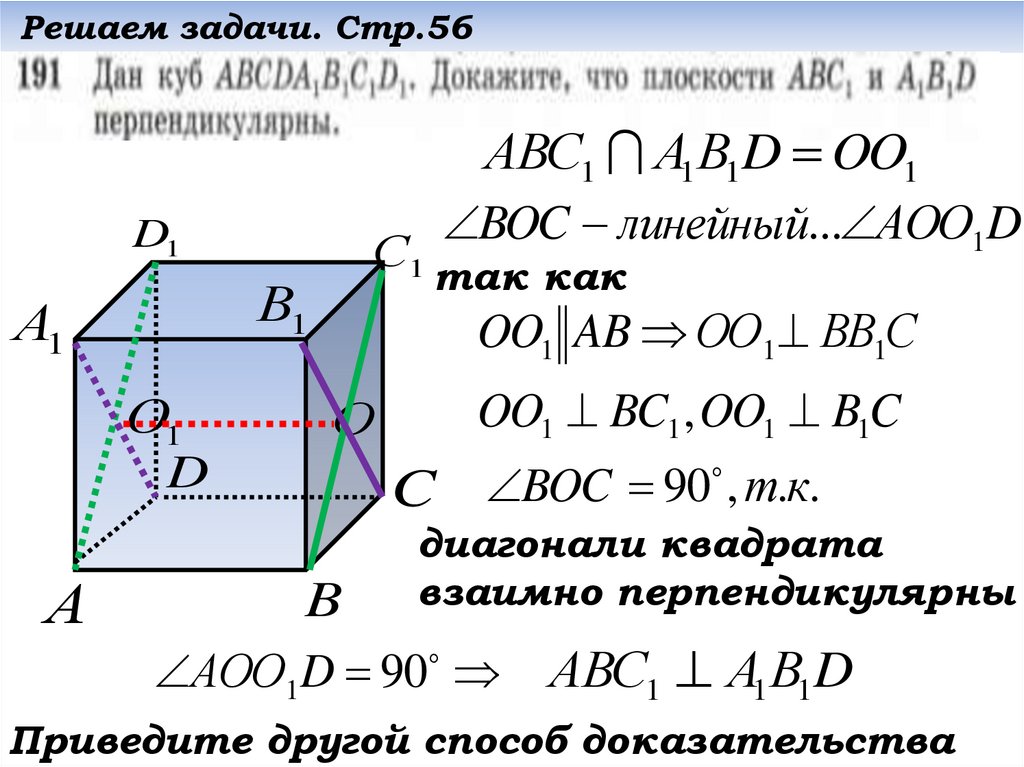
АОО1D 90 АВС1 А1В1D
Приведите другой способ доказательства

37.

Решаем задачи. Стр.56
D1
В1
А1
О1
D
А
Так как ОО1 проходит
С1 через середины диагоналей
боковых граней, то OO1 AB
AB ВВ1С OO1 BВ1С
OO1 ОB
О
C
B
ОB ОО1 , ОВ В1С , ОО1 В1С О
ВО А1В1D

38.

Решаем задачи. Стр.56
С1
D1
В1
А1
О1
D
А
AB ВВ1С OO1 BВ1С
О
B
Так как ОО1 проходит через
середины диагоналей боковых
граней, то OO1 AB
OO1 ОB
ОB ОО1 , ОВ В1С , ОО1 В1С О
C ВО А1В1D
Плоскость АВС1 проходит через прямую
ВО А В D , следовательно АВС А В D
1 1
1
1 1

39.

Домашнее задание
п.24 учить,
стр. 54, № 189,192-195.