Рекурсия

1.

Рекурсия
Лектор: Завьялов Олег Геннадьевич
кандидат физико-математических наук, доцент

2. Циклы и алгоритмы для матриц

Алгоритмом называется совокупность инструкций о том, как
решить некоторую задачу.
Руководство к использованию нового устройства – тоже можно
назвать инструкцией.
Многие алгоритмы содержат периодически повторяющиеся
процессы. Например, при умножении двух матриц размера
n n используется определенная процедура нахождения
элементов матрицы произведения, которая повторяется n2
раз.

3. Процедура цикла перечисления

4. Пример

n
Чтобы найти сумму
S p (i )
i 1
В итоге получается S.
, необходимо:

5. Пример

Вычислить M = r n .

6. Пример

Вычислить p(a), где p(x) - полином, используя схему
Горнера.
Полином:
Алгоритм вычисления S=p(a), где
p x an x n an 1 x n 1 ... a2 x 2 a1 x a0
Алгоритм имеет вид:

7. Определение

Даны частичные упорядочения 1 и 2 .
Упорядочение 2 называется топологической сортировкой
упорядочения 1 , если 2 является полным упорядочением, и
всякий раз, когда a 2 b, тогда a 2 b.
Алгоритм нахождения топологической сортировки для
упорядочения 1 на множестве S:
находим произвольный минимальный элемент частичного
упорядочения и объявляем его минимальным элементом
полного упорядочения;
Затем выбираем другой минимальный элемент и объявляем его
следующим элементом в полном упорядочении и т.д.
Это действие повторяется, пока все элементы множества не
будут выбраны. Всегда выбирают минимальный элемент,
поэтому если в исходном упорядочении a b, то это
соотношение будет иметь место и в новом упорядочении, так
как a будет выбрано первым.

8. Этот алгоритм формально:

9. Определение

Если А = [Aij] – матрица размера m n, то
произведение этой матрицы на скаляр а есть
матрица [Вij] = а [Aij] .
Алгоритм нахождения этого произведения:

10. Определение

Если А = [Aij] и В = [Вij] – матрица размера m n, то
сумма А + В - есть матрица С = [Сij] размера m n,
где Сij = Aij +Вij .
Алгоритм нахождения суммы двух матриц А и В
размера m n :

11. Алгоритм умножения матриц А и В размера m  p и p  n

Алгоритм умножения матриц А и В размера m p и p n
Мощность

12. Рекурсивный метод

Непосредственное задание функции при помощи
формулы, как правило, является
предпочтительным.
Однако, функцию необходимо задавать при помощи
“рекурсивного метода”. Из принципа индукции
следует, что если
1) Функция задана для некоторого данного
начального значения а (обычно 0 или 1),
2) Когда функция задана для некоторого значения k
большего а, она задана также для значения k +1.
Тем самым функция определена для всех целых
чисел, больших а.

13. Определение

Рассмотрим функцию f(n) = an, определенную на
множестве неотрицательных целых чисел.
Её можно задать как произведение n чисел, каждое
из которых равно а.
Функция допускает также и рекурсивное определение

14. Пример

Рассмотрим функцию n! , определенную на
множестве неотрицательных целых чисел.
n! = 1 2 3 n.
Ее моно задать как произведение n чисел, каждое из
которых равно а.
Функция допускает также и рекурсивное определение:

15.

При переходе к рекурсивному определению функция
“факториал” принимает вид:
Компьютерная программа может быть описана так:

16. Пример

Последовательность чисел Фибоначчи.
Первые десять членов последовательности:
1, 1, 2, 3, 5, 8, 13, 21, 34 и 55.
Первый и второй элементы равны 1, а каждый следующий
равен сумме двух предыдущих.
Процедура Фиб(n) описывает программу вычисления значения nго члена последовательности чисел Фибоначчи:
(процедура крайне неэффективна, хотя имеет простой вид)

17. Пример

Последовательность чисел Каталана задается
формулой
Если последовательность начинается 0-го члена, то
первые 11 элементов последовательности числа:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796.
Функция Кат рекурсивно задано так:

18. Определение

Вычислим сначала
Затем
0!
Кат 0
1
1! 0!

19. Две задачи, которые возникают для чисел Каталана

Пусть задан выпуклый (n + 2) –угольник.
Число способов разбиения такого многоугольника на
треугольники, путем соединения вершин многоугольника с
использованием n – 1 отрезка, равно значению Кат(n).
Для треугольника (n=1) существует только один способ
образовать треугольник с использованием линий, и Кат(1)=1.
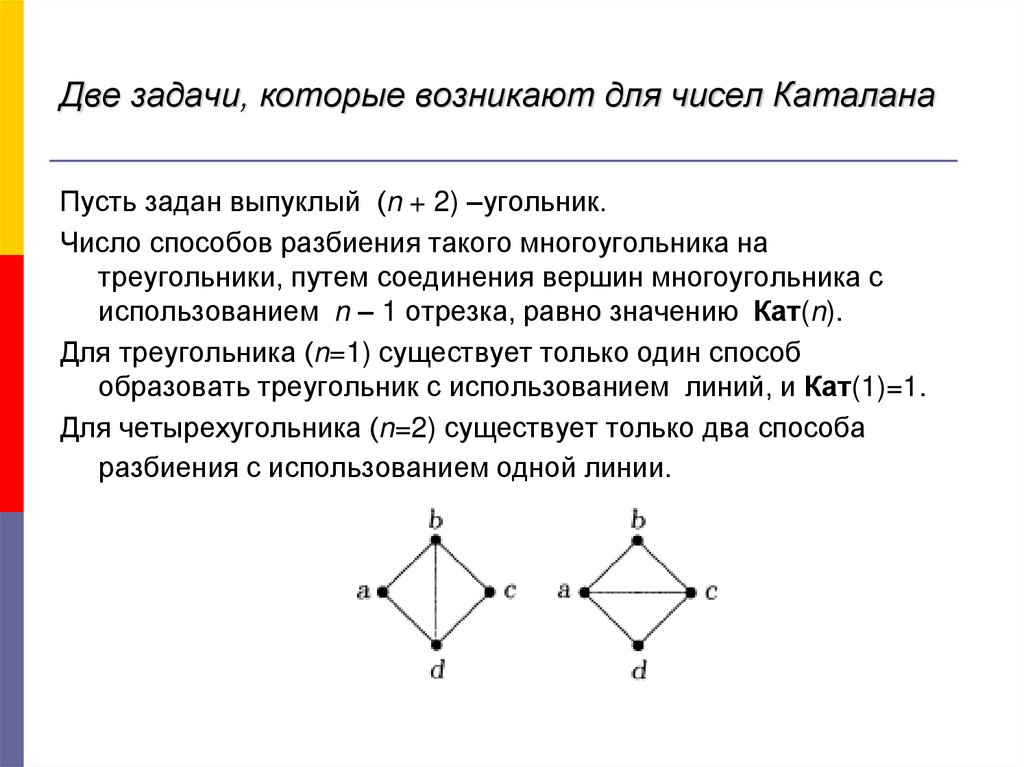
Для четырехугольника (n=2) существует только два способа
разбиения с использованием одной линии.

20. Определение

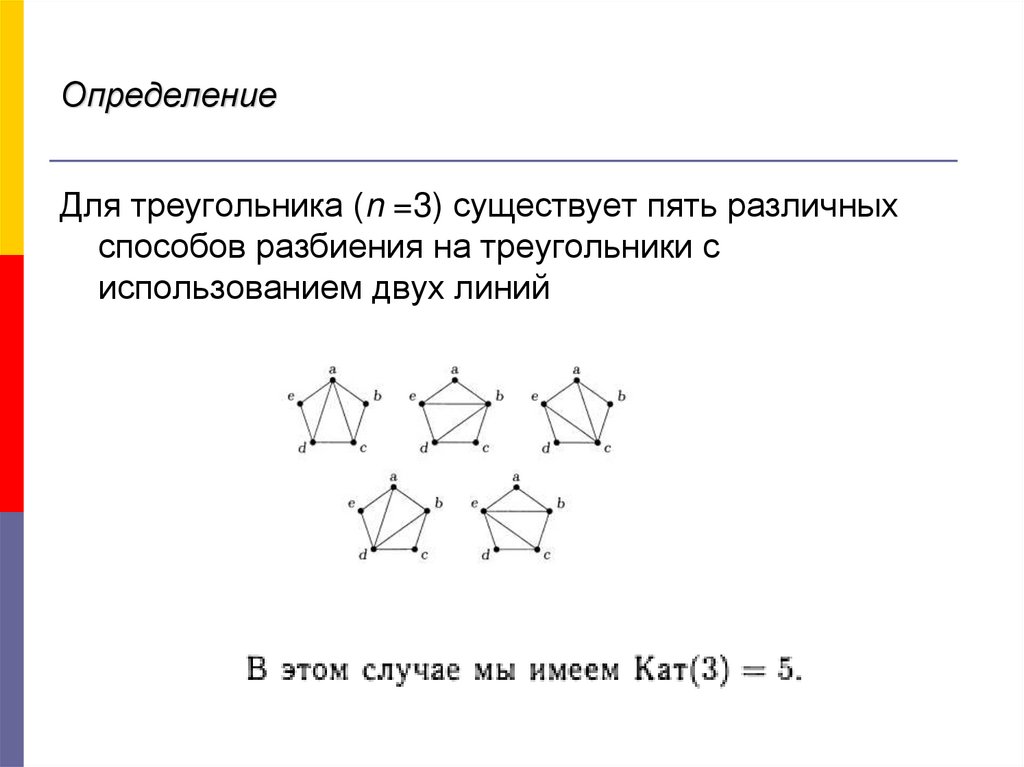
Для треугольника (n =3) существует пять различных
способов разбиения на треугольники с
использованием двух линий

21. 2. Число способов, которыми можно расставить n пар скобок в выражении a1, a2, a3, …, an, an+1

так, чтобы получить n произведений пар чисел, равно
Кат(n).
При n=1 имеется только один способ, а именно:
(a1a2).
При n=2 имеется два способа: ((a1a2)a3) и (a1(a2a3)) .
При n=3 имеется пять способов: (((a1a2)a3)a4),
(a1(a2(a3a4))), ((a1a2)(a3a4)), ((a1(a2a3))a4) и
(a1(a2a3)a4)).

22. Пример

Функция Аккермана – Аккер: N N N.
Функция определена рекурсивно на N N , где N –
множество целых неотрицательных чисел:
Процедуру вычисления функции Аккермана можно
описать следующим образом:

23. Пример

Рассмотрим функцию, которая выражает величину ежегодной
ренты, когда сумма Р инвестируется в течение n периодов с
процентной ставкой i за один период. Подсчет производится
в конце каждого периода.
Если сумма P выражается десятичным числом, то в конце
периода объем инвестиции будет равен основной сумме плюс
начисленные проценты. Проценты, начисляемые за первый
период, составляют iP, так что общий объем инвестиции
будет равен P + iP =( 1 + i) P.

24. Продолжение примера

Например, если 1000 ден. ед. инвестировано на год под 5%, то I
= 0,05. Тогда в конце года общий объем вклада будет 1000
ден.ед. инвестированных плюс 0,05 1000=50 ден.ед.
Если другие деньги не вкладываются, то в конце второго
периода вклад составит (1 + i) P + i (1 + i) P = (1 + i)2 P,
Где i (1 + i) P - проценты от вложения (1 + i) P .
По прошествии 2-х лет инвестиции в 1000 ден.ед. дает сумму
1050. По прошествии n лет начальная инвестиция вырастет
до (1 + i)nP .

25.

Пусть сумма Р инвестируется в конце каждого периода в течение
n периодов с процентной ставкой i за каждый период.
Подсчет производится в конце каждого периода.
На только что вложенную сумму Р проценты не начисляются,
поэтому она остается равной Р.
Вклад Р, инвестированный в предыдущий период, вместе с
начисленными процентами составит
(1 + i)P.
Общая сумма вклада, накопленная за n период:
P + (1 + i)P + (1 + i)2P +…+ (1 + i)n -1P = P S(n, i)

26.

S(n, i) – геометрическая прогрессия.
S n, i 1 1 i 1 i ... 1 i
n 1
2
1 i 1 1 i 1
S n, i
n
n
1 i 1
r n 1
r 1
i
Более эффективно можно вычислить рекурсивно:
S n, i 1 1 i 1 i 1 i ... 1 i
2
3
n
1 1 i 1 1 i 1 i ... 1 i
1 1 i S n, i
S 1, i 1;
2
n 1
S n, i 1 1 i S n 1, i для n 1

27. Рекурсивный алгоритм, который не является определением рекурсивной функции

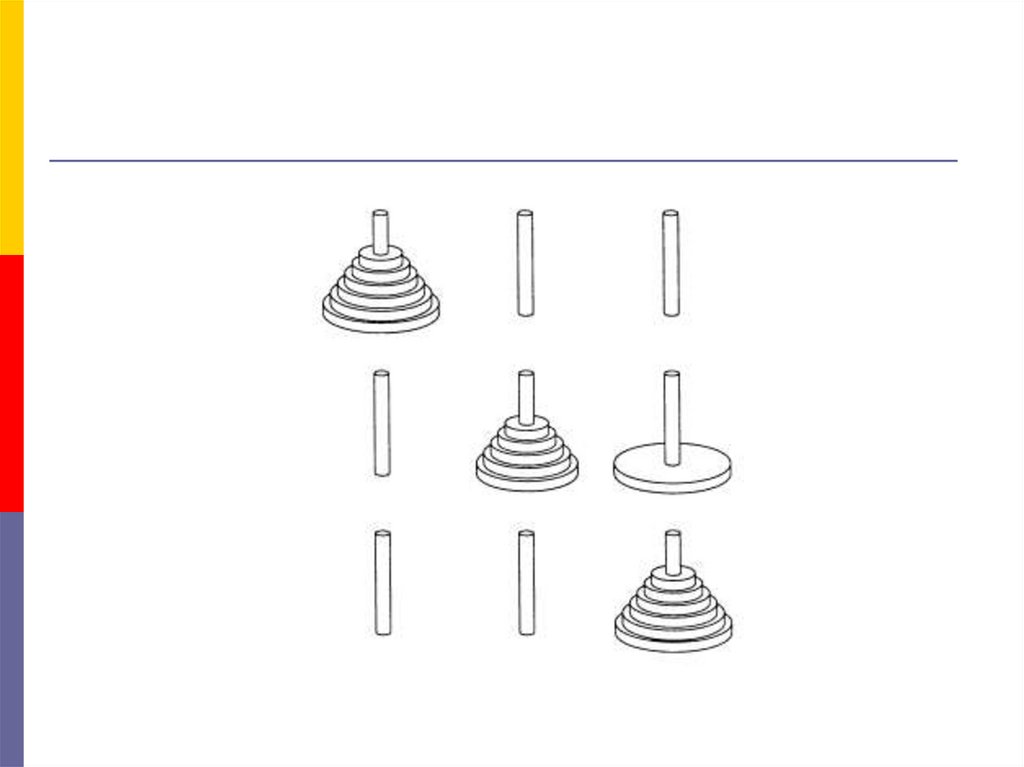
Старая легенда: в задаче о Ханойской башне фигурируют три
стержня и набор дисков разного диаметра. Диски нанизаны на
один из стержней в порядке убывания их диаметра. Причем
диск наибольшего диаметра находится в самом низу, а диск
наименьшего – самый верхний.
Задача состоит в том, чтобы переместить все диски на другой
стержень по одному за раз, и диск большего диаметра нельзя
помещать над диском меньшего диаметра.
Если на стержне имеется, например, шесть дисков и известно,
как переместить пять их них, то пять верхних дисков можно
переместить на средний стержень, затем переместить
последний диск на свободный стержень, а затем поместить
пять дисков со среднего стержня поверх самого большого
диска.

28.

29. Определение

Алгоритм перемещения n дисков с первого стержня на третий.
Перенумеруем стержни от 1 до 3 и отождествим их с
переменными А, В и С, которые могут принимать значения от
1 до 3.

30.

Например, если n=3, начинают с Хан(1, 3, 3), так что А=1, В=2, С=3.
Находясь внутри процедуры Хан(1, 3, 3), вызывают процедуру Хан(1, 2,
2), которая может переместить два верхних диска на стержень 2.
Из процедуры Хан(1, 2, 2) вызываем процедуру Хан(1, 3, 1), которая должна
переместить верхний диск со стержня 1 на стержень 3. Далее вызывают
Хан(1, 2, 1), чтобы переместить второй диск на стержень 2.
Затем вызывают Хан(1, 3, 1), чтобы переместить второй диск со стержня 1
на стержень 3.
Затем вызывают Хан(3, 2, 1) , перемещая верхний диск со стержня 2 поверх
второго диска на стержне 3. Возвращаются к Хан(1, 3, 3) и вызывают
Хан(1, 3, 1), перемещая самый нижний диск со стержня 3 на стержень 1.
Затем вызываю Хан(2, 3, 2) для перемещения двух дисков со стержня 2 на
стержень 3. В этот момент А=2, В=1, С=3. Из процедуры Хан(2, 3, 2)
вызывают Хан(2, 1, 1) для перемещения верхнего диска со стержня 2 на
стержень 1.
Далее вызывают Хан(2, 3, 1) для перемещения второго диска со стержня 2 а
стержень 3. Наконец, вызывают Хан(1, 3, 1) для перемещения верхнего
диска со стержня 1 поверх всех дисков на стержне 3.
Завершается выполнение процедур Хан(2, 3, 2) и Хан(1, 3, 3), игра
заканчивается.

31. Легенда гласит, что на один из трех бриллиантовых стержней нанизаны 64 золотых диска.

Некий монах перемещает диски согласно правилу со скоростью одно
движение за секунду. Согласно легенде, когда монах выполнит
эту миссию, наступит конец света.
Спрашивается, как долго продлится этот процесс?
Построим функцию для вычисления количества движений (секунд),
необходимых для переноса n дисков с одного стержня на другой.
Обозначим эту функцию Н. Известно, что если n=1, то для переноса
диска с одного стержня на другой требуется одно движение.
Н(1)=1.
Допустим, что Н(k-1) известно. Тогда Н(k) – количество движений,
необходимых для переноса со стержня 1 на стержень 3.
Складывается из Н(k-1) движений, необходимых для переноса k-1
диска со стержня 1 на стержень 2, одного движения по переносу
нижнего диска со стержня 1 на стержень 3 и H(k-1) движений,
необходимых для переноса k-1 –го диска со стержня 2 на
стержень 3.
Рекурсивное соотношение H(k) = 2H(k-1)+1 задает искомую
функцию.

32. Несколько первых значений Н:

Предположим, что
H(n) = 2n – 1.
Предположим, что утверждение справедливо для n=k+1
H(k+1) = 2k+1 -1
H(k+1) = 2H(k) + 1 = 2 (2k -1) +1=2k+1 -1

33. Определение

В примерах осуществлялся переход от рекурсивного
описания функции к непосредственному. Для этого
вычислялось несколько первых значений функции и
по ним определялся вид выражения, задающего
функцию непосредственно.
Такая процедура называется исключением
рекурсии, или решением рекурсивной функции.

34. Пример

Исключить рекурсию из рекурсивного определения:

35.

Затем, что f(k) = f(k - 1) + k
Таким образом,
определению.
n n 1
f n
2
удовлетворяет рекурсивному

36.

Последний слайд лекции
!!