Similar presentations:
Рекурсия. Нахождение корня нелинейного уравнения методом половинного деления
1.
Рекурсия2.
РекурсияРекурсивным называется объект, частично
состоящий или определяемый с помощью
самого себя.
Рекурсия – это процесс повторения действий
внутри этого элемента.
Например, если два зеркала установить друг
напротив друга, то возникающее в них
изображение – есть бесконечная рекурсия.
Алгоритм задан рекурсивно, если состоит из:
• Одного или нескольких условий выхода из
тела рекурсивной функции – базиса
рекурсии;
• Шага рекурсии, который в конечном счете
должен приводить к выходу из рекурсии.
3.
Дано:Пример
(нахождение
корня
нелинейного
уравнения
методом
половинного
деления)
a и b – границы отрезка, на котором существует корень
уравнения;
eps – заданная точность;
f(x) – монотонная функция.
Алгоритм нахождения корня:
а) Находится середина отрезка x1 = (a+b)/2, точка x1 считается
первым приближенным значением корня;
б) Корень находится на том из двух отрезков [a;x1] и [x1;b], где
функция имеет на границах разные знаки.
Сдвигается та граница, где отрезок не имеет корня(граница a,
если отрезок [a;x1] не имеет корня; граница b, если отрезок
[x1;b] не имеет корня).
в) Новый отрезок [a,b] снова делится пополам (середина
данного отрезка – x2). x2 - новое приближенное значение
корня;
г) Повторяем пункты б и в до тех пор , пока не выполнится
условие |x2 – x1| < eps;
Повторение пунктов б, в и г является рекурсией.
4.
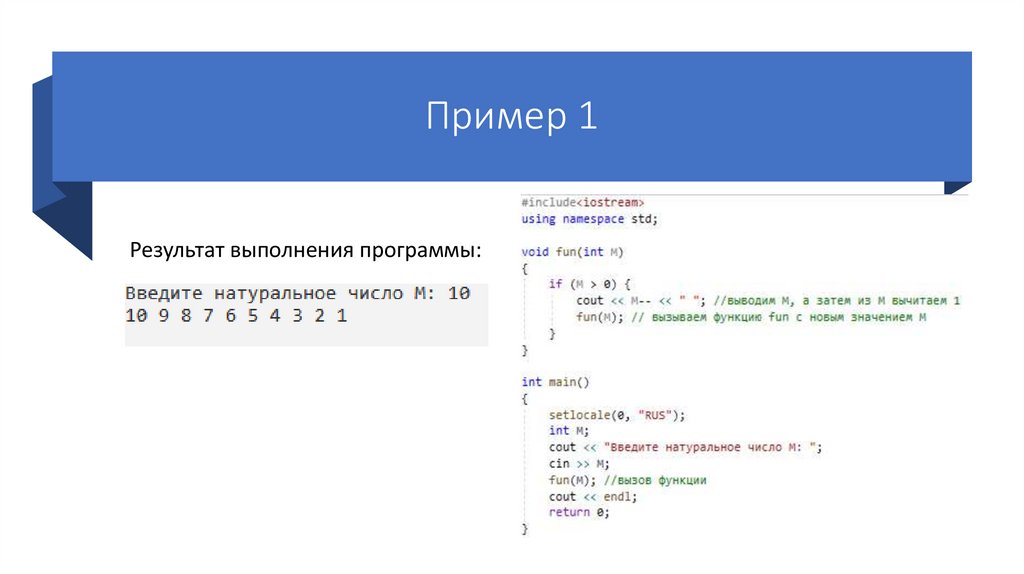
Пример 1Рассматривается пример, в котором числа натурального
ряда от 1 до M (где M > 0) выводятся в обратном
порядке.
1. Создаётся функция fun, её параметром является число
М, которое выводится на экран.
2. В функции main() вводится натуральное число М.
3. Далее вызывается функция fun(M), где значение М
используется в качестве параметра.
4. В теле функции fun выполняется проверка на
попадание числа М в заданное ограничение М > 0.
Если М удовлетворяет условию М > 0, то выводится М, а
затем из М вычитается 1 (М изменяется на каждом
шаге).
Далее снова вызывается функция fun(M)
5. Пункт 4 выполняется до тех пор, пока будет
выполняться условие M > 0.
5.
Пример 1Результат выполнения программы:
6.
• Простая (прямая) рекурсияВиды
рекурсии
• Сложная (косвенная)
рекурсия
• Хвостовая рекурсия
7.
Простая (прямая) рекурсияПримером простой рекурсии является вычисление наибольшего
общего делителя двух чисел.
Наибольший общий делитель (НОД) двух чисел – это наибольшее
число, на которое оба числа делятся без остатка.
Постановка задачи:
Даны два натуральных числа m и n. Реализовать программу, которая
будет находить наибольший общий делитель чисел m и n.
8.
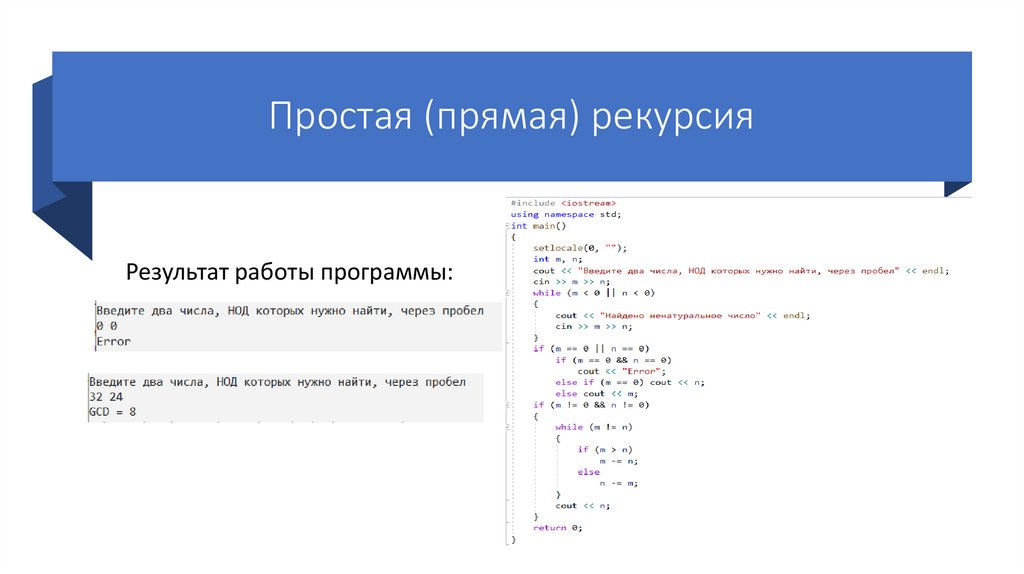
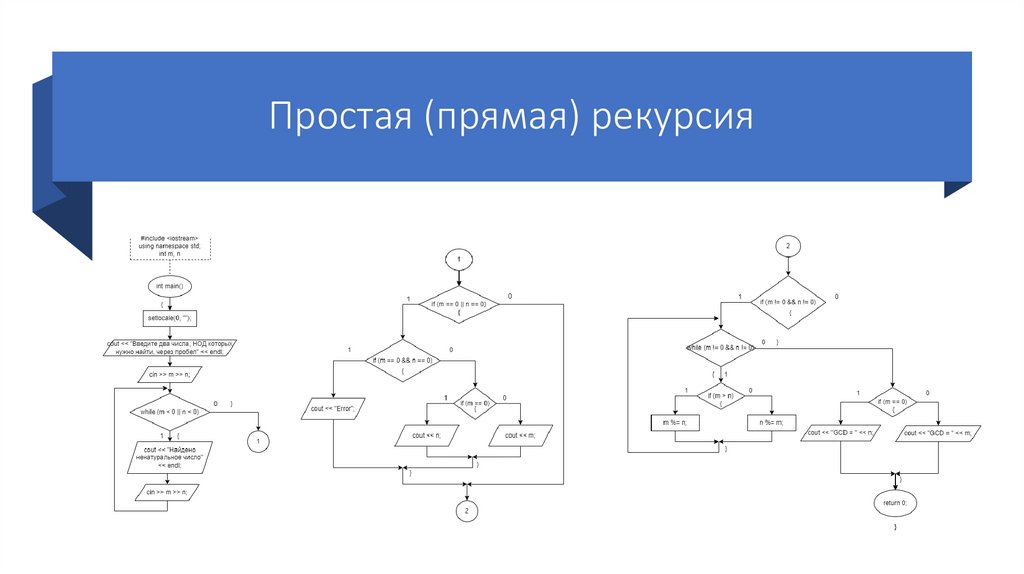
Простая (прямая) рекурсияАлгоритм решения задачи:
1. Вводятся два числа – m и n.
2. Выполняется проверка на натуральность чисел.
3. Если оба числа равны 0, выводится сообщение об ошибке.
4. Если одно из чисел равно 0, выводится ненулевое число.
5. Выполняется алгоритм Евклида с условием выхода из цикла m == n.
6. После выполнения тела цикла m и n равны, выводится любое из
полученных чисел (например, n).
9.
Простая (прямая) рекурсияРассмотрим работу программы на примере чисел 14 и 21.
1. Пользователь вводит числа 14 и 21 (m = 14, n = 21).
2. В цикле while (m != n) последовательно из большего числа
вычитается меньшее:
а) 14 < 21, n = 21 – 14 = 7, m = 14;
б) 14 > 7, m = 14 – 7 = 7, n = 7;
в) 7 == 7, цикл завершается;
3. Выводится любое из этих чисел (например, GCD = n, n = 7).
10.
Простая (прямая) рекурсия11.
Простая (прямая) рекурсияРезультат работы программы:
12.
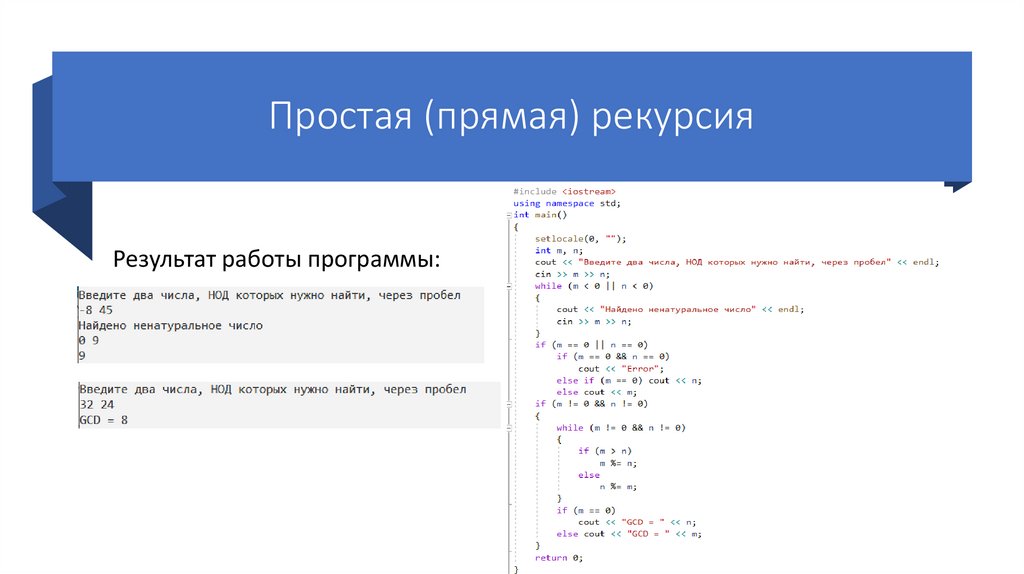
Простая (прямая) рекурсияСуществует и другой вариант нахождения НОД двух натуральных чисел.
Алгоритм решения задачи:
1. Вводятся два числа – m и n.
2. Выполняется проверка на натуральность чисел.
3. Если m и n равны 0, выводится сообщение об ошибке.
4. Если одно из чисел не равно 0, выводится ненулевое.
5. Иначе выполняется тело цикла с условием выхода из него m == 0 || n == 0.
6. В цикле проверяется условие (m > n). Если оно истинно, находится остаток от
деления m на n, иначе – остаток от деления n на m.
7. После работы цикла выводится то число, значение которого не равно 0.
13.
Простая (прямая) рекурсияРассмотрим работу программы на примере чисел 14 и 21.
1. Пользователь вводит числа 14 и 21 (m = 14, n = 21).
2. В цикле while (m != 0 && n != 0):
а) 14 < 21, n = 21 % 14 = 7, m = 14;
б) 14 > 7, m = 14 % 7 = 0, n = 7;
в) m == 0, n == 7, цикл завершается;
3. Выводится n = 7, так как его значение не равно 0.
14.
Простая (прямая) рекурсия15.
Простая (прямая) рекурсияРезультат работы программы:
16.
Сложная (косвенная) рекурсияСигнатура функции - это описание её заголовка, в которое обычно входят:
•Имя функцииСложная рекурсия – это процесс, в котором одна функция вызывает вторую, а
•Число, тип и та,
порядок
следования
передаваемых
в неё параметров
(в т.ч.
и то как именно
они передаются,
по ссылке или
в свою
очередь,
вызывает первую.
При этом
функция,
описываемая
первой,
по значению)
должна вызывать еще не описанную вторую функцию, чтобы это было возможно
•Тип возвращаемого значения
требуется
описание
функции.
Функция А вызывает
функцию
В, а та, всигнатуры
свою очередь,
вызывает А (сложная рекурсия). При этом оказывается, что
функции
- это
частьеще
общего
объявления
функции,
котораятребуется
позволяет
описываемая Сигнатура
первой процедура
должна
вызвать
не описанную.
Чтобы это
было возможно,
использовать
сигнатуру. понять компилятору, что эта функция существует.
Таким образом,
сигнатура сигнатуры
- это все чтосодержит:
нужно знать о функции вызывающему её коду.
Описание
•Имя функции
•Число, тип и порядок следования передаваемых в неё параметров (в т.ч. и то,
как именно они передаются, по ссылке или по значению)
•Тип возвращаемого значения
Таким образом, сигнатура - это все, что нужно знать о функции вызывающему её
коду.
17.
Сложная (косвенная) рекурсияПостановка задачи:
Даны две функции F и G. Определить, чему равно
значение F(4) по формуле F(n) = F(n - 1) + G(n - 2).
1. F(4) = F(3) + G(2);
2. G(2) = 1;
3. F(3) = F(2) + G(1);
4. F(2) = 1;
5. G(1) = 1;
6. F(3) = 1 + 1 = 2;
7. F(4) = 2 + 1 = 3.
int G(int);
int F(int x)
{
if (x > 2)
return F(x - 1) + G(x - 2);
else return 1;
}
int G (int x)
{
if (x > 2)
return G(x - 1) + F(x - 2);
else return 1;
}
int main()
{
setlocale(0, "");
cout << "Значение F(4) = "<< F(4);
return 0;
}
18.
Сложная (косвенная) рекурсияРезультат выполнения программы:
int G(int);
int F(int x)
{
if (x > 2)
return F(x - 1) + G(x - 2);
else return 1;
}
int G (int x)
{
if (x > 2)
return G(x - 1) + F(x - 2);
else return 1;
}
int main()
{
setlocale(0, "");
cout << "Значение F(4) = "<< F(4);
return 0;
}
19.
Префиксная и постфиксная формы записирекурсивной функции
Префиксная форма – cначала
происходит рекурсивный вызов,
потом – действия.
Постановка задачи:
Дано натуральное число N.
Реализовать программу, в результате
выполнения которой будут выведены
числа от 0 до N.
Результат выполнения
программы при num = 7:
20.
Префиксная и постфиксная формы записирекурсивной функции
Постфиксная (хвостовая) форма:
Сначала выполняются действия,
потом – рекурсивный вызов.
Постановка задачи:
Дано натуральное число N.
Реализовать программу, в результате
выполнения которой будут выведены
числа от N до 0.
Результат выполнения
программы при num = 7.
21.
Числа ФибоначчиЧисла Фибоначчи — это ряд, состоящий из целых чисел. Их особенность
заключается в том, что каждый элемент представляет собой сумму двух
предыдущих чисел (кроме первого и второго числа).
Последовательность Фибоначчи начинается с 0 и 1. Продолжить ряд легко: 0,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и так до бесконечности.
Задача на вычисление чисел Фибоначчи является примером простой
рекурсии.
Постановка задачи:
Реализовать рекурсивную функцию для вычисления n-го числа Фибоначчи.
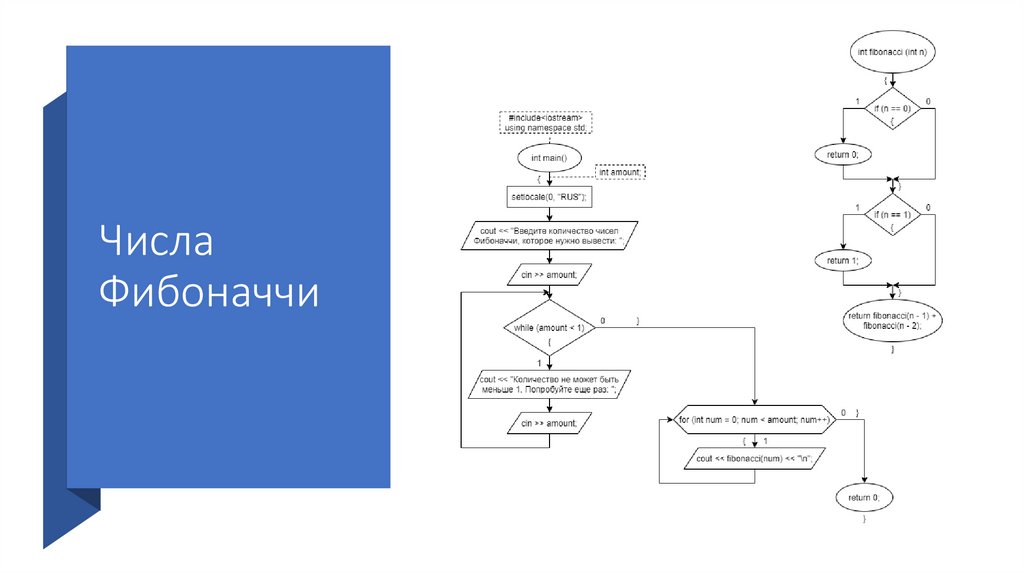
22.
Числа ФибоначчиФункция fibonacci() вычисляет n-ое число
Фибоначчи. Если в функцию передано
значение 0, возвращается 0; если передано
1 – возвращается 1. Иначе возвращается
сумма двух предыдущих чисел.
23.
Числа ФибоначчиПользователь вводит значение количества
чисел Фибоначчи, которые нужно вывести.
Если введенное значение меньше 1,
пользователь осуществляет ввод до тех пор,
пока значение не удовлетворит заданному
условию (amount >= 1).
24.
Числа ФибоначчиПри помощи цикла for осуществляется
вывод заданного количества чисел
Фибоначчи.
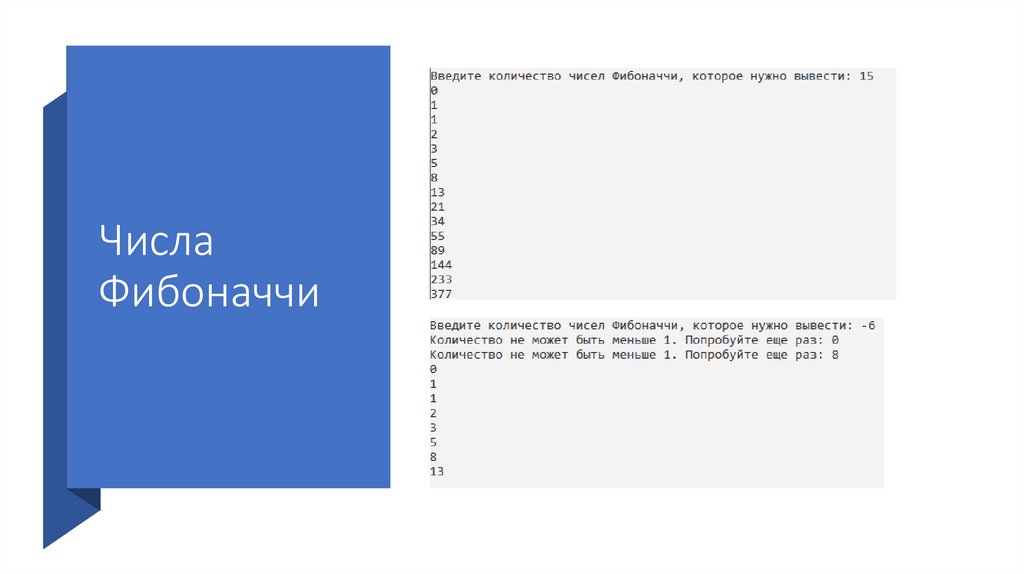
25.
ЧислаФибоначчи
26.
ЧислаФибоначчи
27.
ЧислаФибоначчи
28.
Ханойская башняПостановка задачи:
Даны 1 стержень с дисками разного размера и 2 пустых стержня. Нужно
переместить диски с одного стержня на другой, перекладывать можно только по
одному диску за ход, складывать диски можно только меньший на больший.
Реализовать программу, которая определяет перестановки этих дисков с помощью
наименьшего количества ходов.
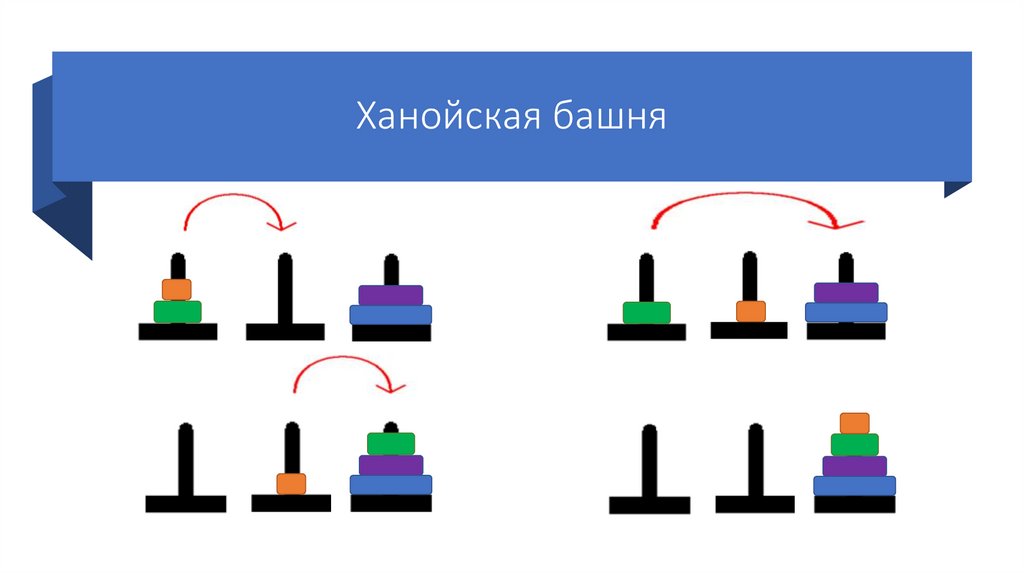
29.
Ханойская башня30.
Ханойская башня31.
Ханойская башня32.
Ханойская башня33.
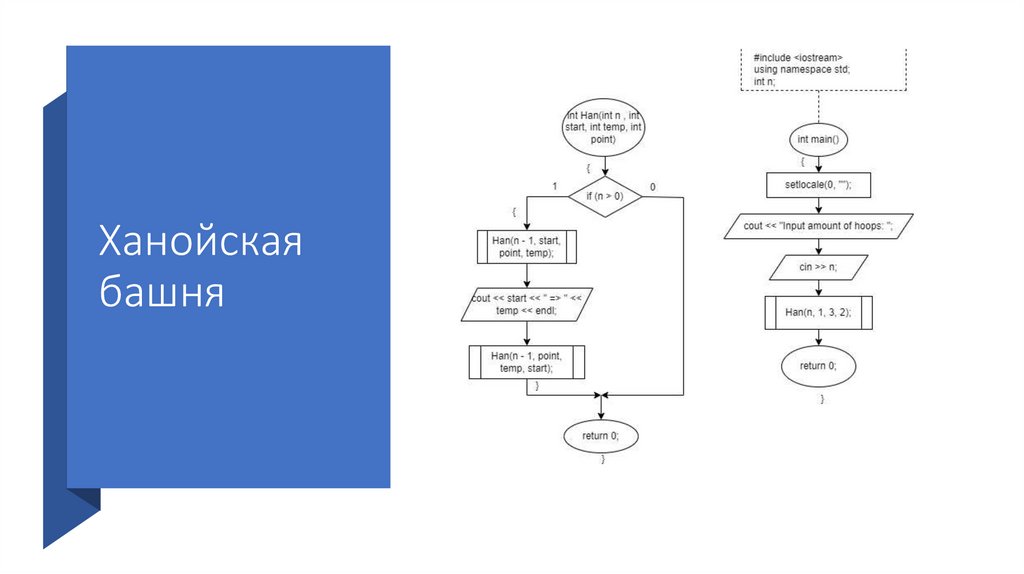
Ханойская башняАнализ задачи:
Нужно решать задачу не с начала, а с конца. Чтобы переложить пирамидку на
нужный стержень, нужно переложить на нужный стержень нижний диск, а
сделать это можно только тогда, когда n – 1 дисков будут на свободном
стержне.
1. Перекладываем n – 1 дисков на свободный стержень.
2. Перекладываем n-ый диск на нужный стержень.
3. Перекладываем n – 1 дисков на нужный стержень.
Чтобы переложить n – 1 дисков, нужно:
1. Перекладываем n – 2 дисков на свободный стержень.
2. Перекладываем n – 1 диск на нужный стержень.
3. Перекладываем n – 2 дисков на нужный стержень.
Рекурсивный алгоритм продолжается до тех пор, пока n не достигнет 0.
34.
Ханойская башняАлгоритм решения задачи для 4 дисков:
1. Нужно переложить 3 диска на
свободный стержень.
2. Переложить 4-ый диск на нужный
стержень.
3. Переложить 3 диска на нужный
стержень.
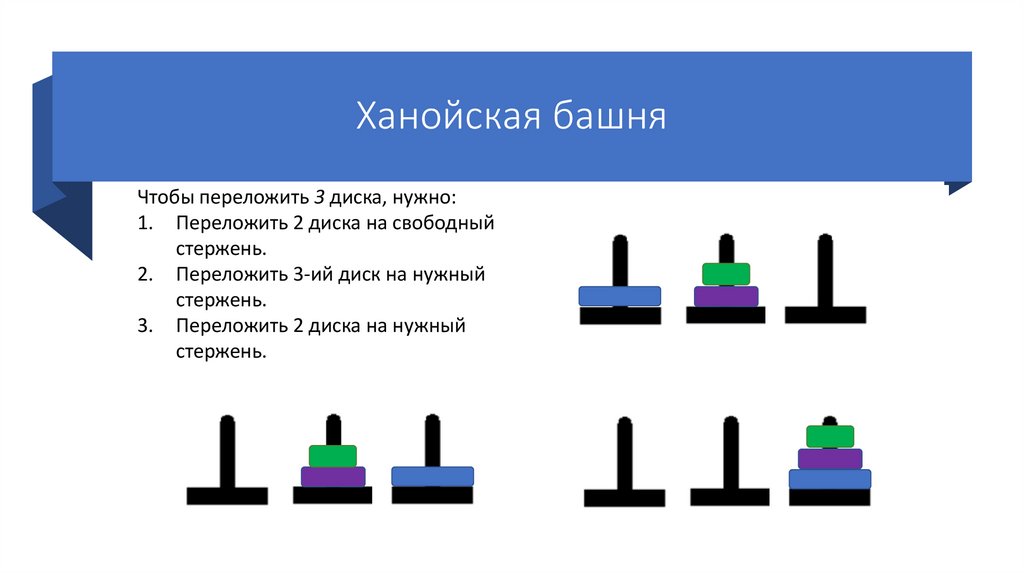
35.
Ханойская башняЧтобы переложить 3 диска, нужно:
1. Переложить 2 диска на свободный
стержень.
2. Переложить 3-ий диск на нужный
стержень.
3. Переложить 2 диска на нужный
стержень.
36.
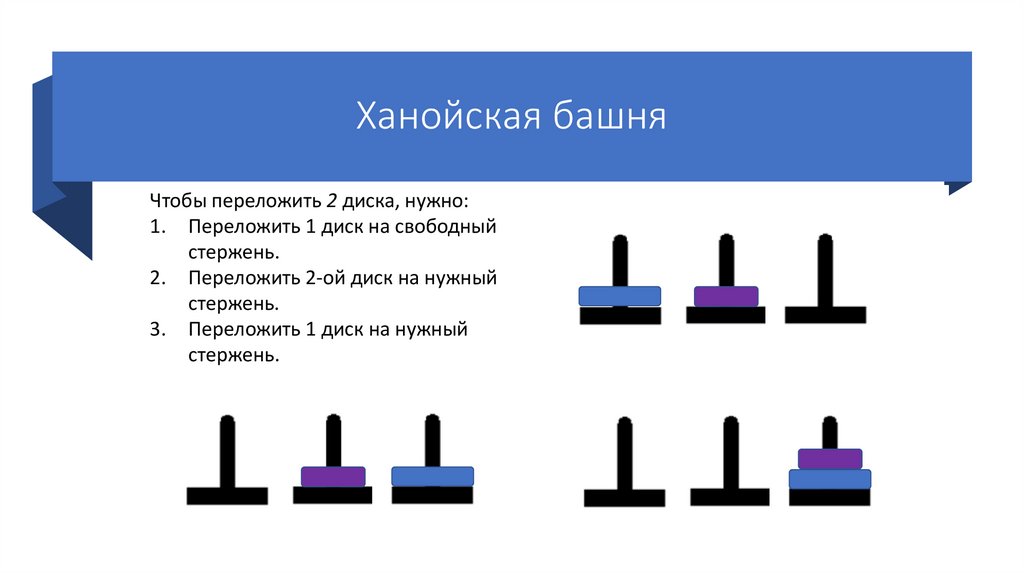
Ханойская башняЧтобы переложить 2 диска, нужно:
1. Переложить 1 диск на свободный
стержень.
2. Переложить 2-ой диск на нужный
стержень.
3. Переложить 1 диск на нужный
стержень.
37.
Ханойскаябашня
38.
Ханойскаябашня
39.
Ханойскаябашня
40.
Задача о восьми ферзяхПостановка задачи:
Реализовать
программу, в которой
реализуется алгоритм
расстановки 8 ферзей
на доске 8х8 так, чтобы
ферзи были
расставлены в каждой
строке и не «били»
друг друга.
Анализ решения задачи:
Ферзь может ходить в любом направлении по горизонтали,
вертикали, диагонали и на любое количество клеток, рубит он так
же, как ходит.
Чтобы ферзи друг друга не «били», на каждой строке, диагонали
и каждом столбце должен находиться один ферзь.
Для расстановки ферзей требуется:
1. Поставить первого ферзя на позицию а1 (первая клетка
первой строки).
2. Перейти на следующую строку и поставить ферзя так, чтобы
первый ферзь его не бил.
3. Если на какой-либо строке поставить ферзя невозможно(так,
чтобы они не «били» друг друга), то возвращаемся на
предыдущую строку и ставим ферзя на следующую клетку
строки.
4. Повторяем пункты 2 и 3, пока не расставим всех ферзей.
41.
Задача овосьми
ферзях
42.
Задача о восьми ферзяхСтавим первого ферзя на позицию a1
(первая клетка первой строки)
Отмечаем крестиками те позиции,
которые этот ферзь «бьет» (вертикаль,
горизонталь, диагональ)
43.
Задача о восьми ферзяхСтавим второго ферзя на первую
возможную клетку второй строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
44.
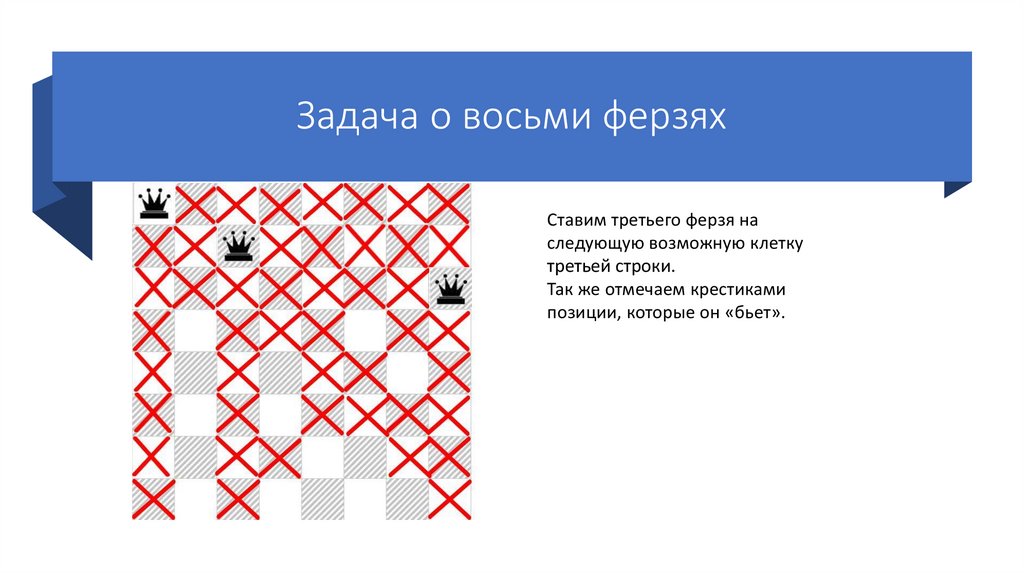
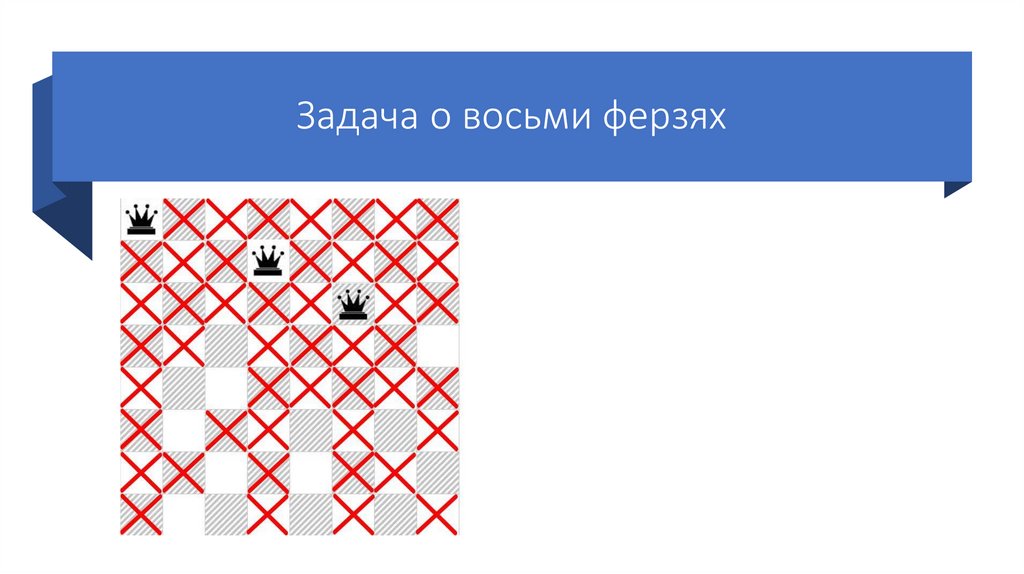
Задача о восьми ферзяхСтавим третьего ферзя на первую
возможную клетку третьей строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
45.
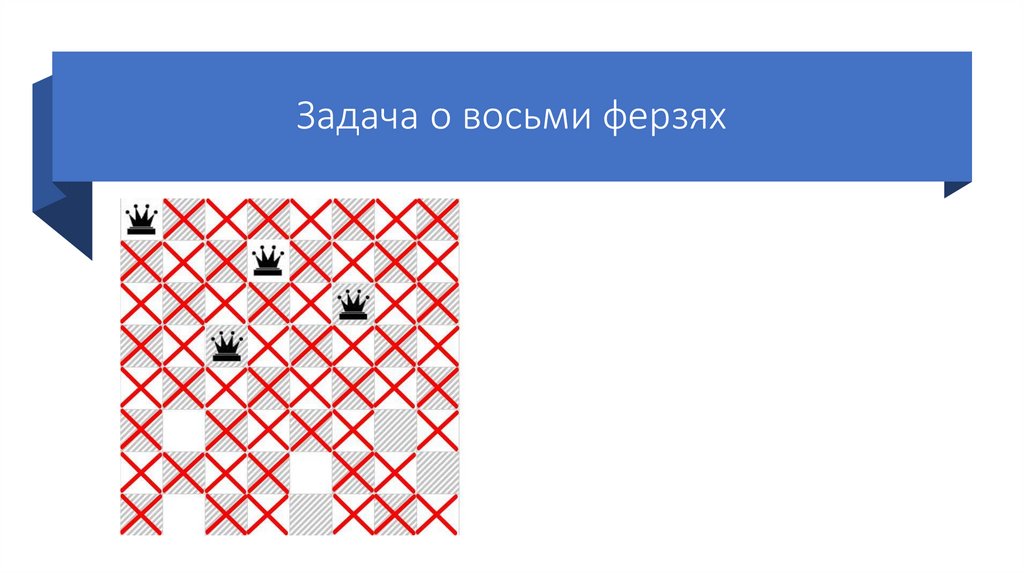
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
46.
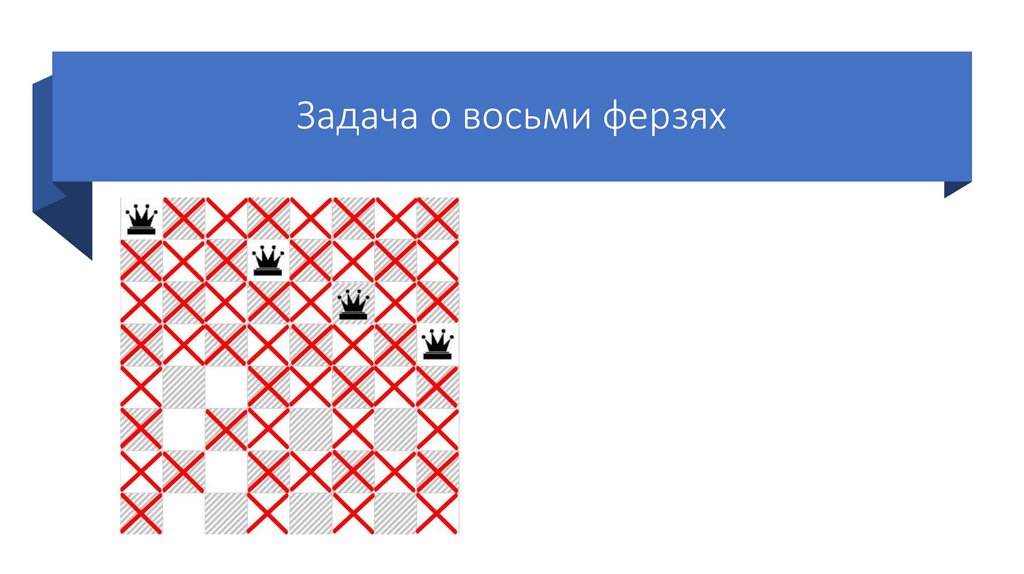
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
47.
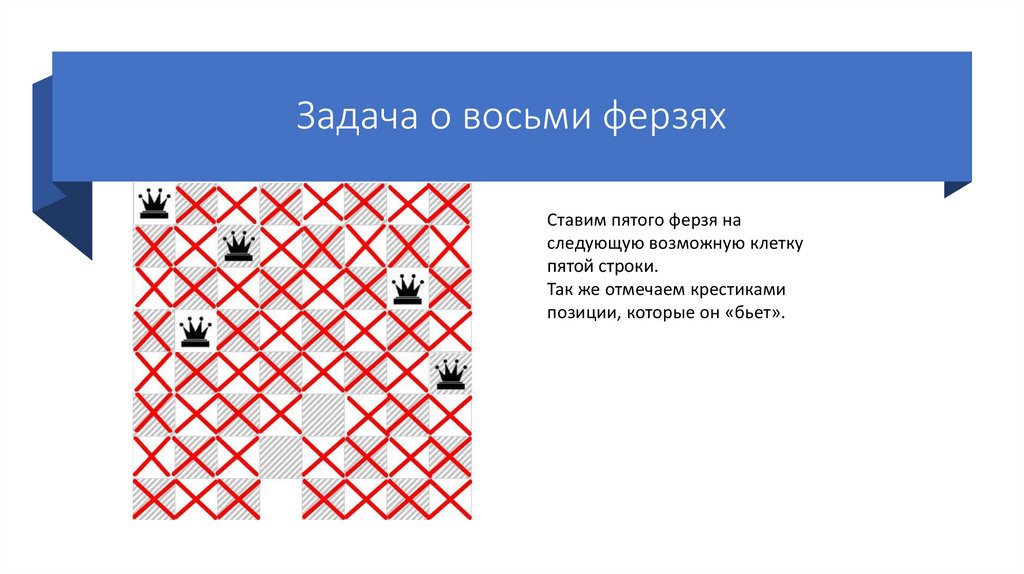
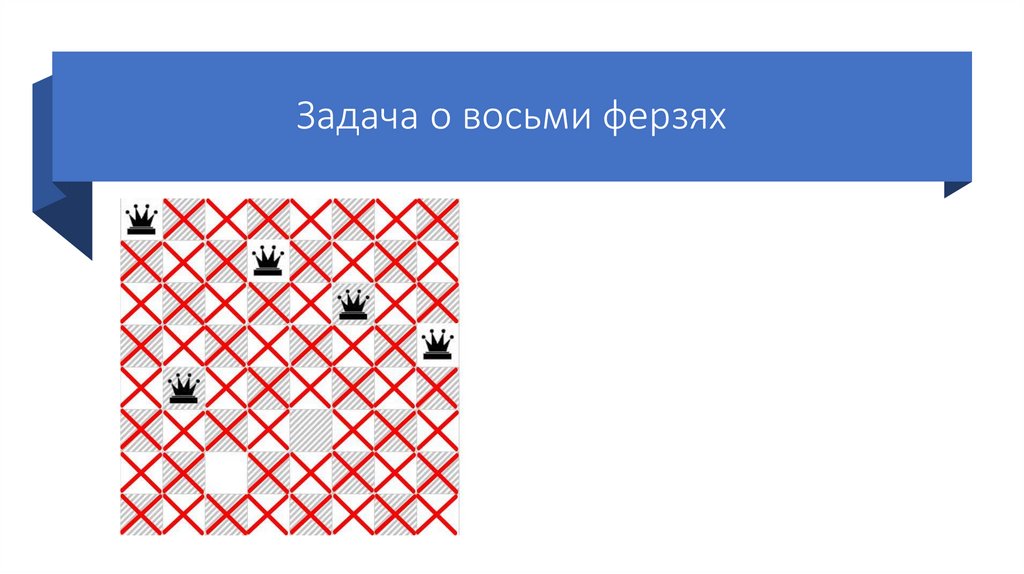
Задача о восьми ферзяхСтавим пятого ферзя на следующую
возможную клетку пятой строки.
Так же отмечаем крестиками позиции,
которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг назад
(переставляем предыдущего ферзя на
следующую возможную клетку своей
строки). Но возможные позиции ферзя
на пятой строке закончились, поэтому
переходим к предыдущему ферзю
(четвертому).
48.
Задача о восьми ферзяхСтавим четвертого ферзя на
следующую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
49.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
50.
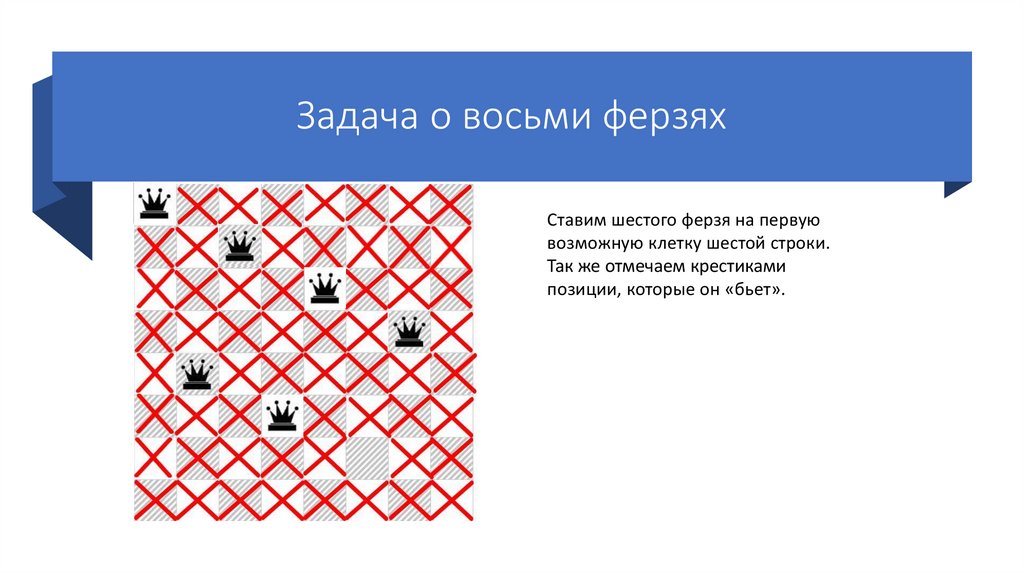
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
51.
Задача о восьми ферзяхСтавим седьмого ферзя на первую
возможную клетку седьмой
строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как восьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 7 и 6 ферзей ставить некуда,
поэтому переставляем 5 ферзя.
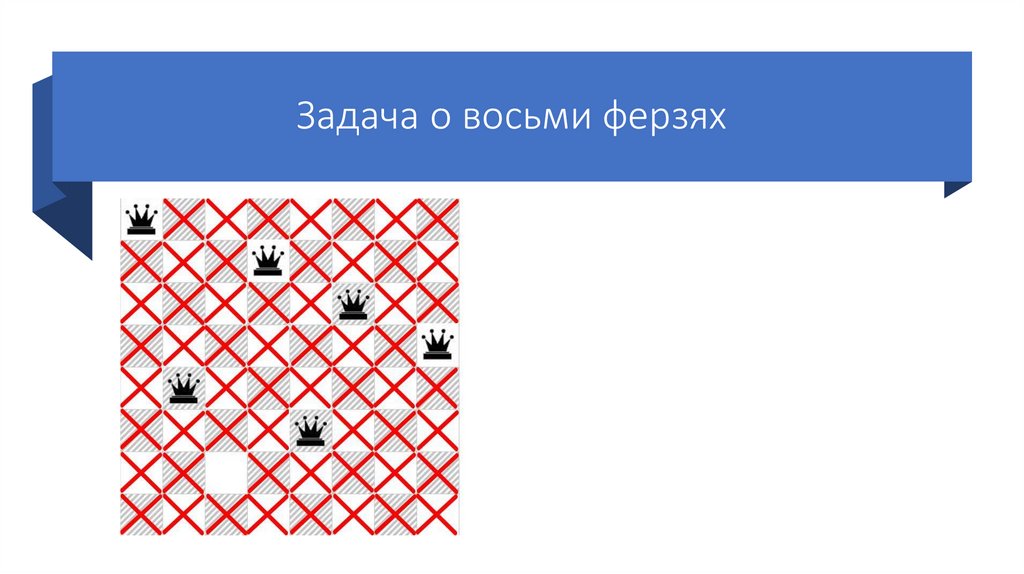
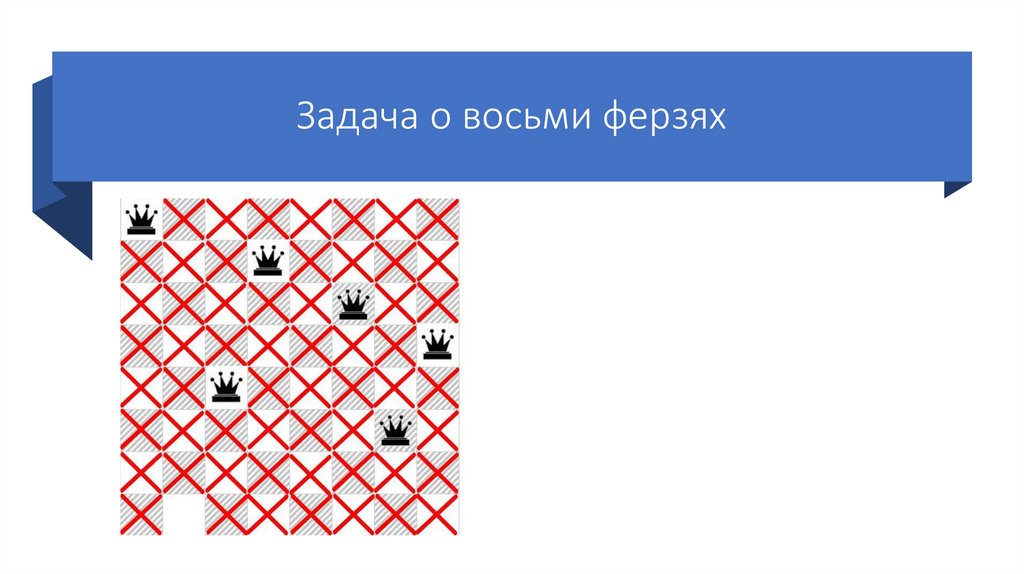
52.
Задача о восьми ферзяхСтавим пятого ферзя на
следующую возможную клетку
пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но возможные позиции четвертого
ферзя закончились, поэтому
возвращаемся еще на шаг назад
(переставляем третьего ферзя)
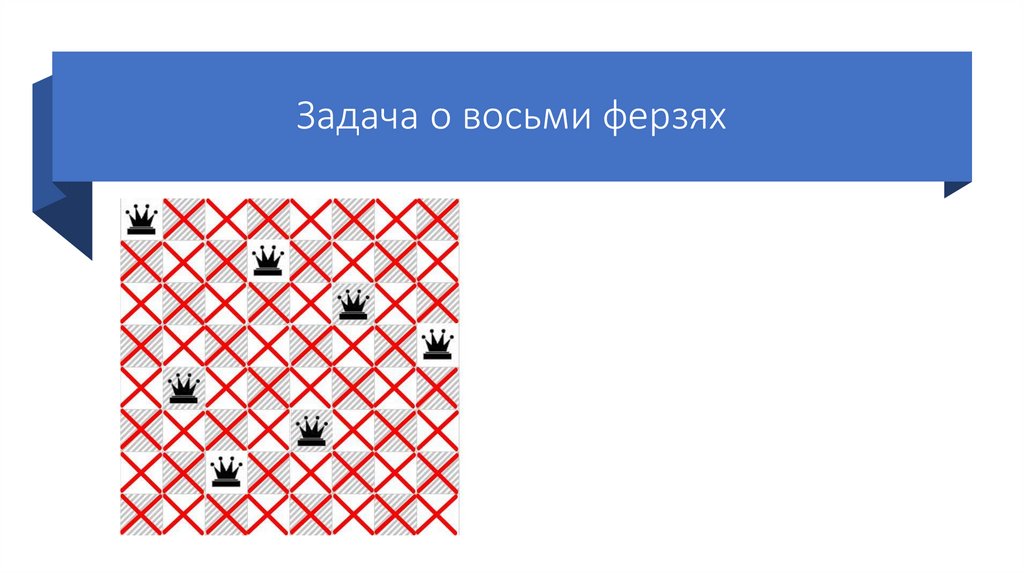
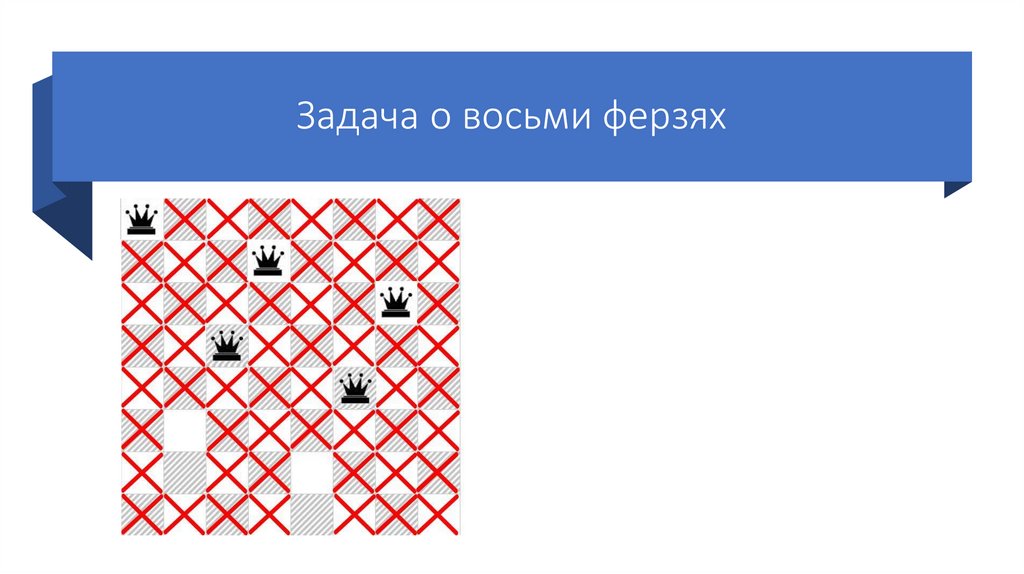
53.
Задача о восьми ферзяхСтавим третьего ферзя на
следующую возможную клетку
третьей строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
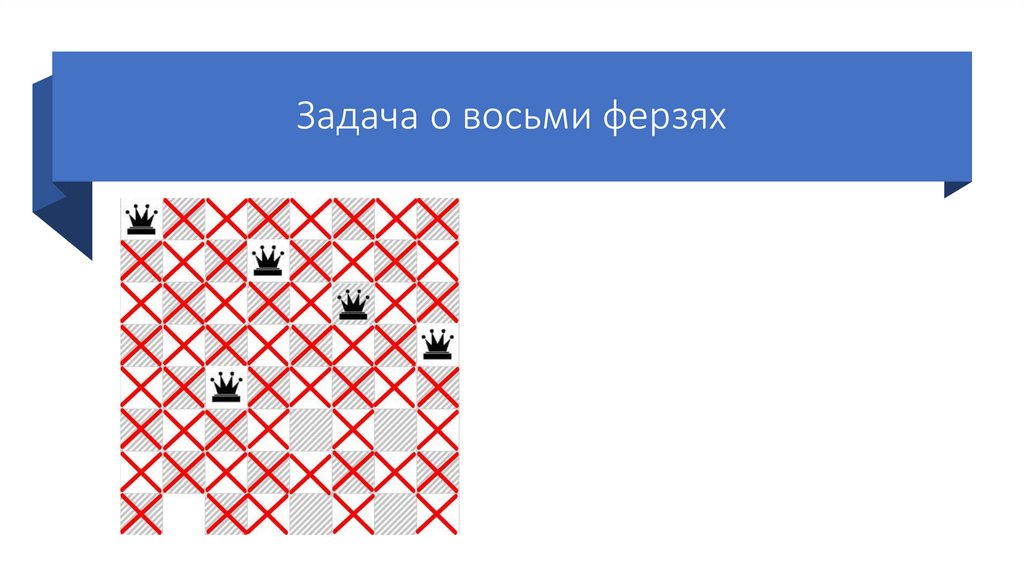
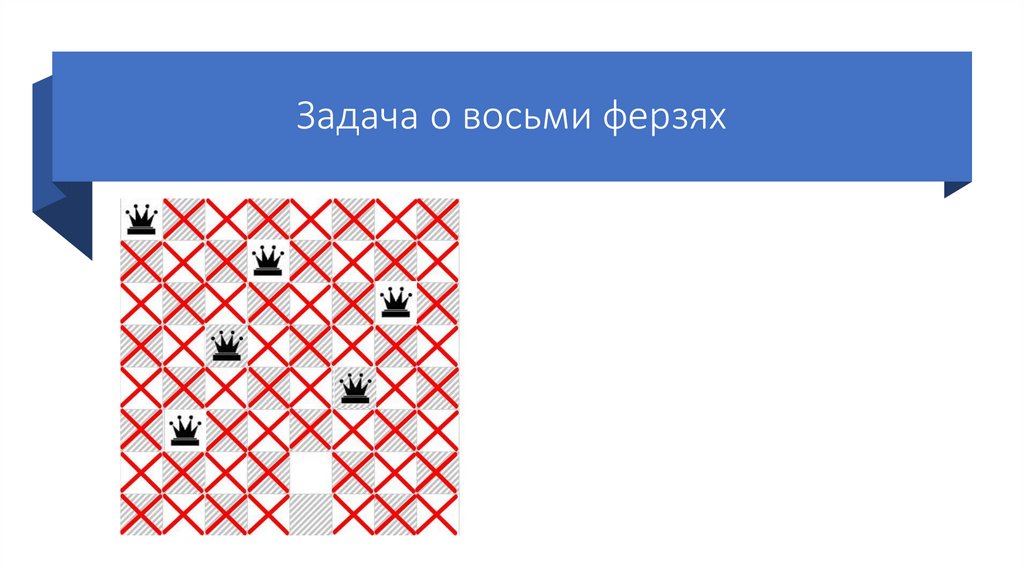
54.
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
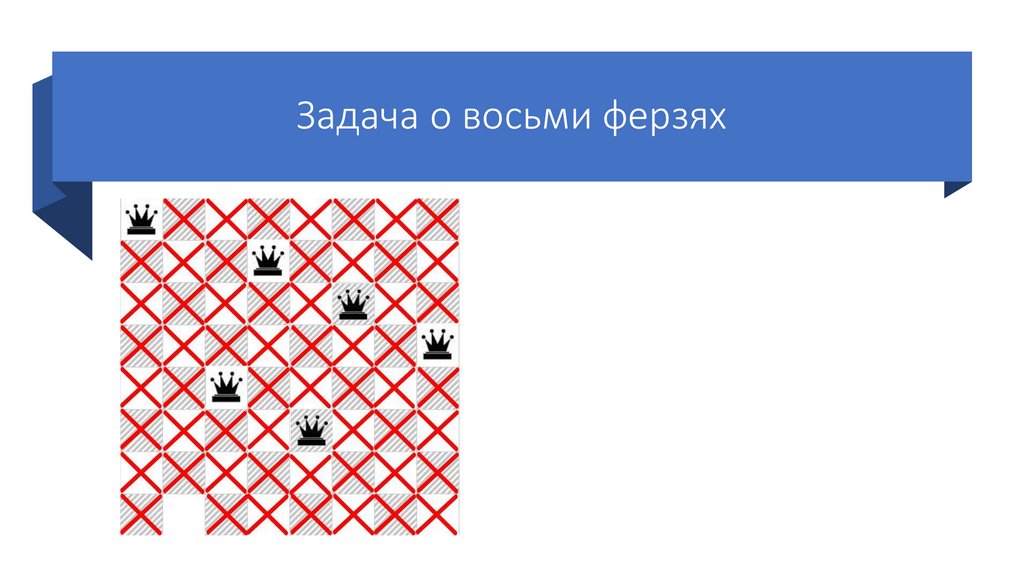
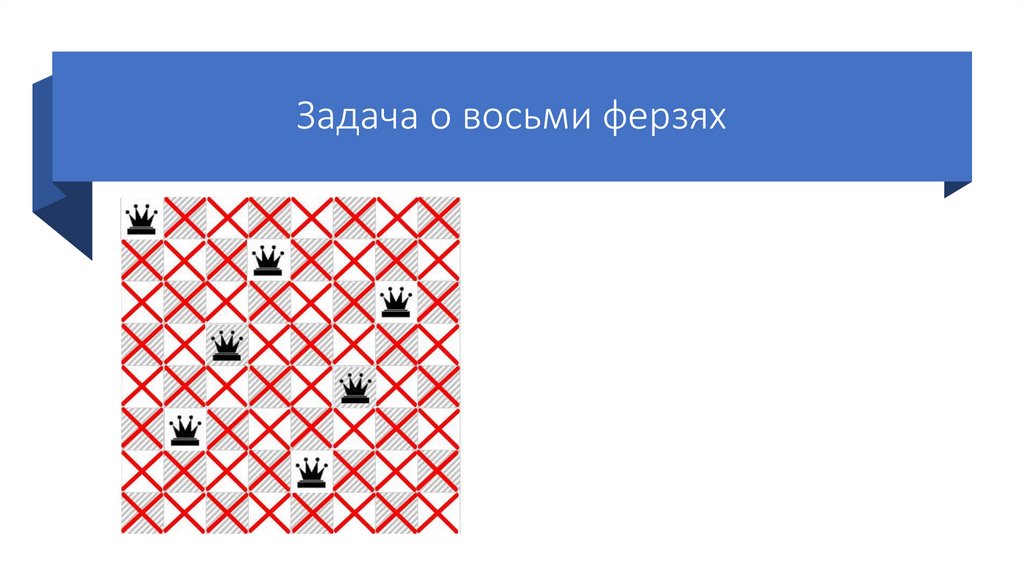
55.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
56.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя поставить уже некуда,
поэтому переставляем 4 ферзя на
следующую возможную позицию.
57.
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
58.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
59.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
60.
Задача о восьми ферзяхСтавим шестого ферзя на
следующую возможную клетку
шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя переставлять уже
некуда, поэтому переставляем на
следующую возможную позицию 4
ферзя.
61.
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
62.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
63.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя тоже некуда ставить,
поэтому переставляем 4 ферзя на
следующую возможную позицию.
64.
Задача о восьми ферзяхСтавим четвертого ферзя на
следующую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
65.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
66.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 и 4 ферзей тоже некуда
ставить, поэтому переставляем 3
ферзя на следующую возможную
позицию.
67.
Задача о восьми ферзяхСтавим третьего ферзя на
следующую возможную клетку
третьей строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
68.
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
69.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
70.
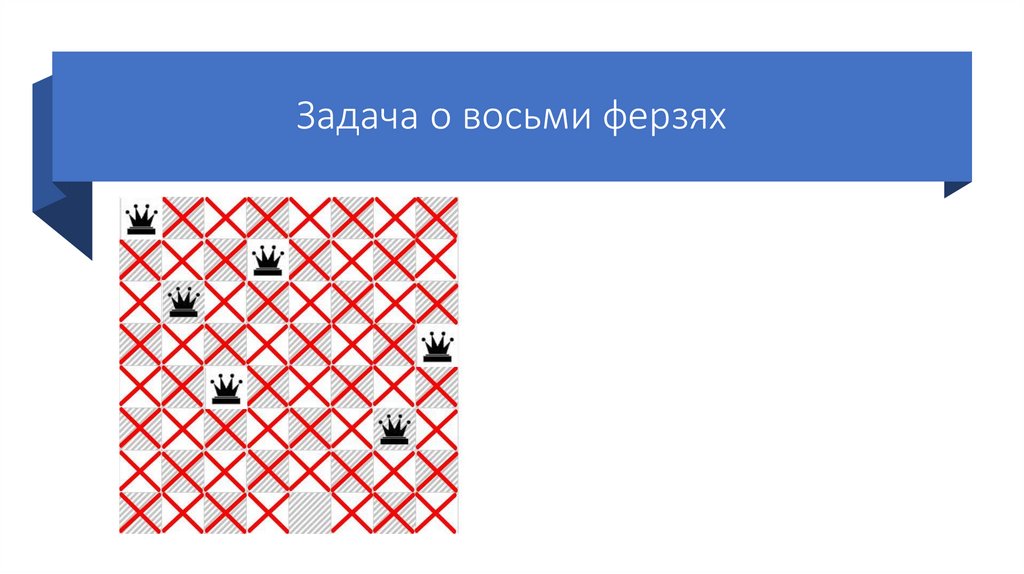
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 6 ферзя тоже некуда поставить,
поэтому переставляем 5 ферзя.
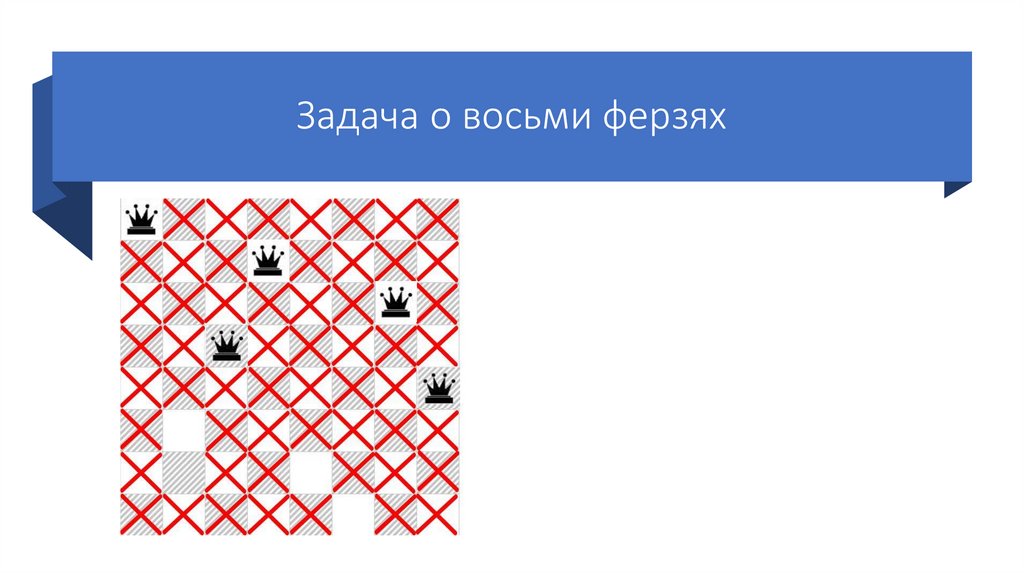
71.
Задача о восьми ферзяхСтавим пятого ферзя на
следующую возможную клетку
пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
72.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как седьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 и 4 ферзей тоже некуда
ставить, поэтому переставляем 3
ферзя на следующую возможную
позицию.
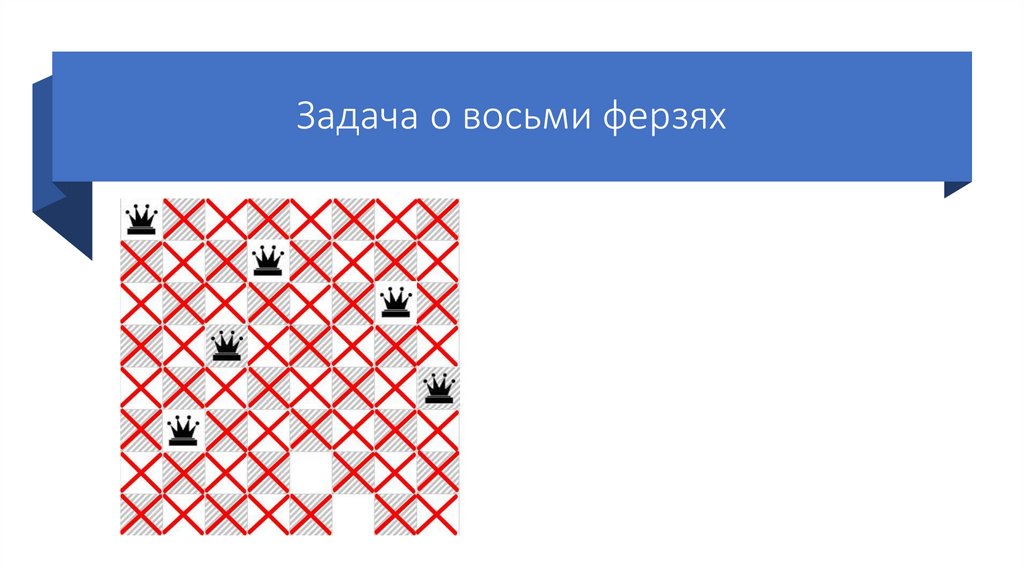
73.
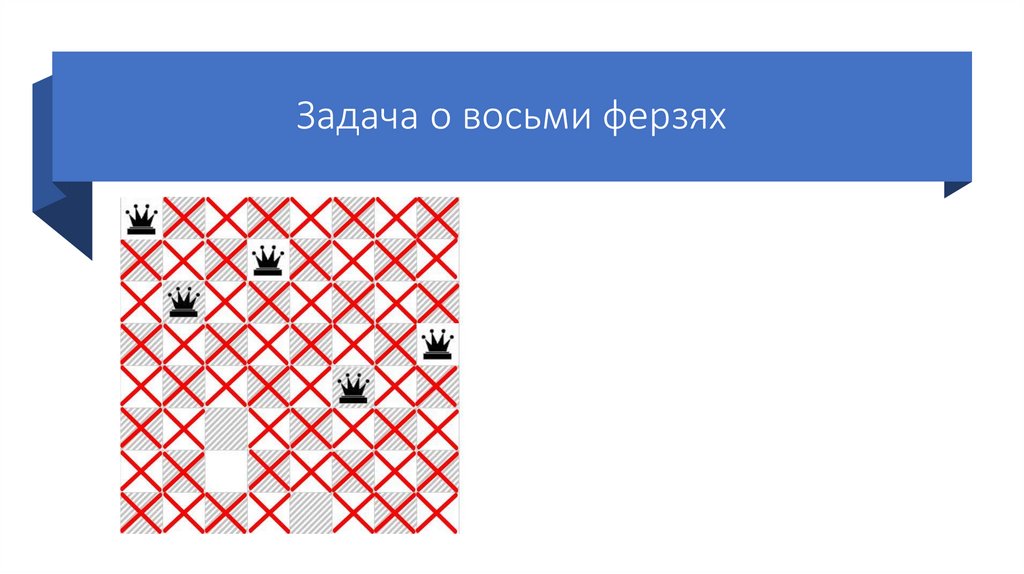
Задача о восьми ферзяхСтавим третьего ферзя на
следующую возможную клетку
третьей строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
74.
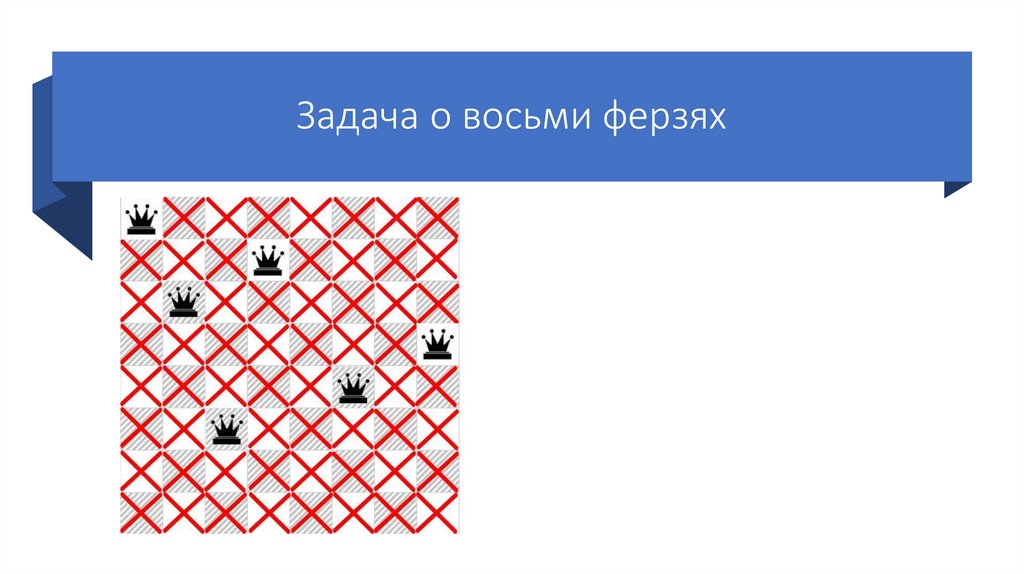
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
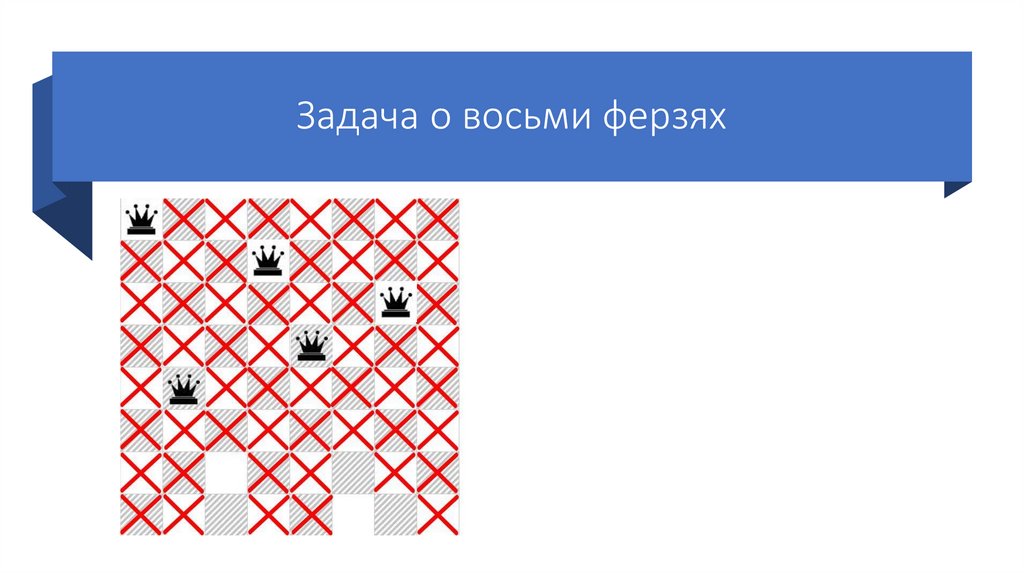
75.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
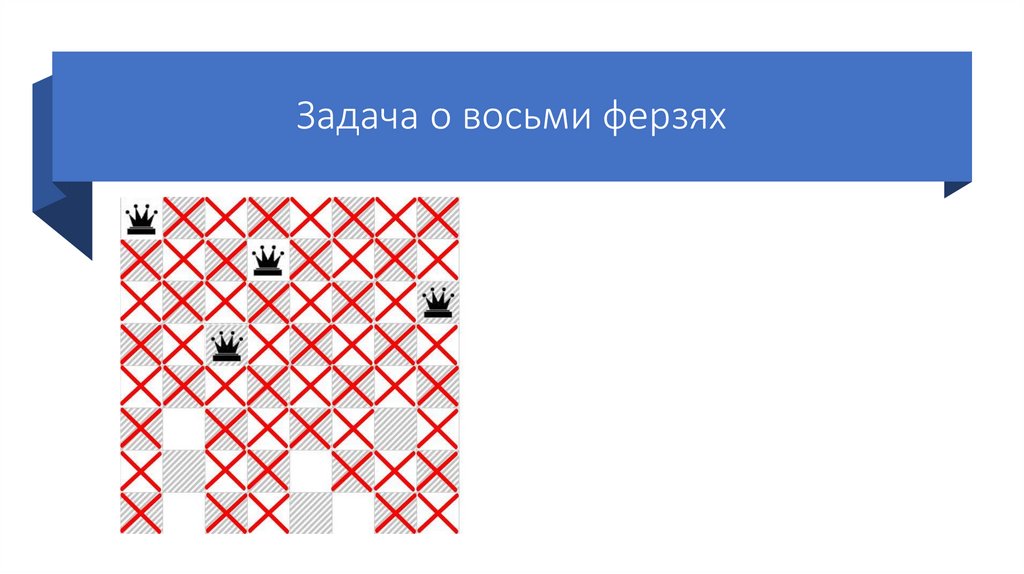
76.
Задача о восьми ферзяхСтавим пятого ферзя на
следующую возможную клетку
пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя тоже ставить некуда,
поэтому переставляем 4 ферзя на
следующую возможную позицию
77.
Задача о восьми ферзяхСтавим четвертого ферзя на
следующую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
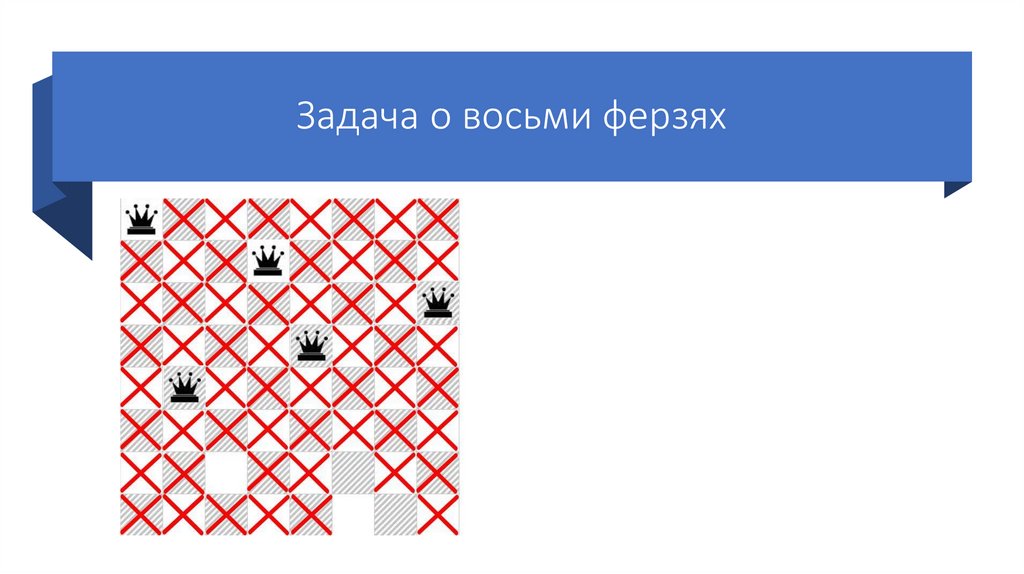
78.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
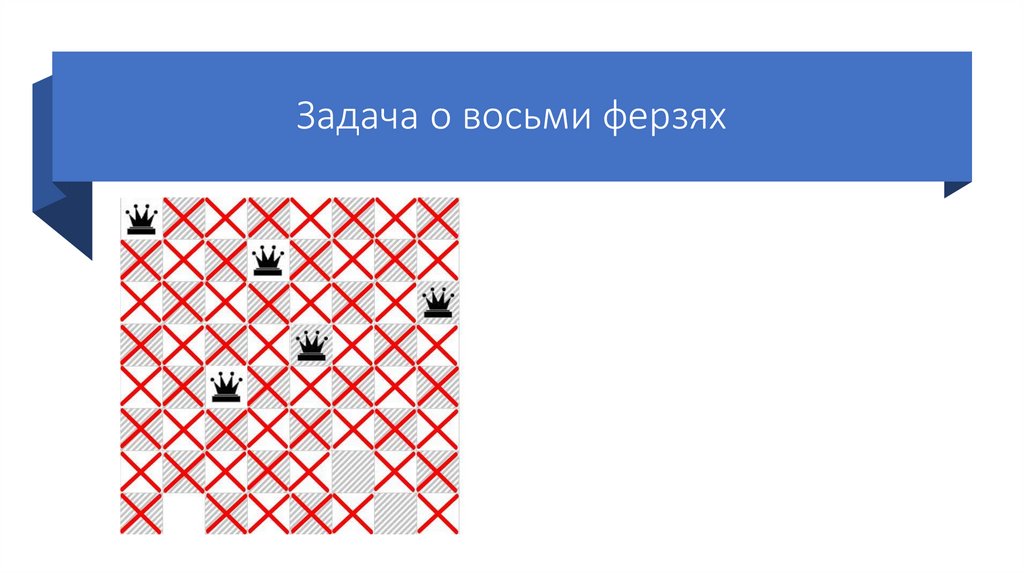
79.
Задача о восьми ферзяхСтавим пятого ферзя на
следующую возможную клетку
пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
80.
Задача о восьми ферзяхСтавим шестого ферзя на первую
возможную клетку шестой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
81.
Задача о восьми ферзяхСтавим седьмого ферзя на первую
возможную клетку седьмой
строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как восьмого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 3, 4, 5 и 6 ферзей тоже некуда
ставить, поэтому переставляем 2
ферзя на следующую возможную
позицию.
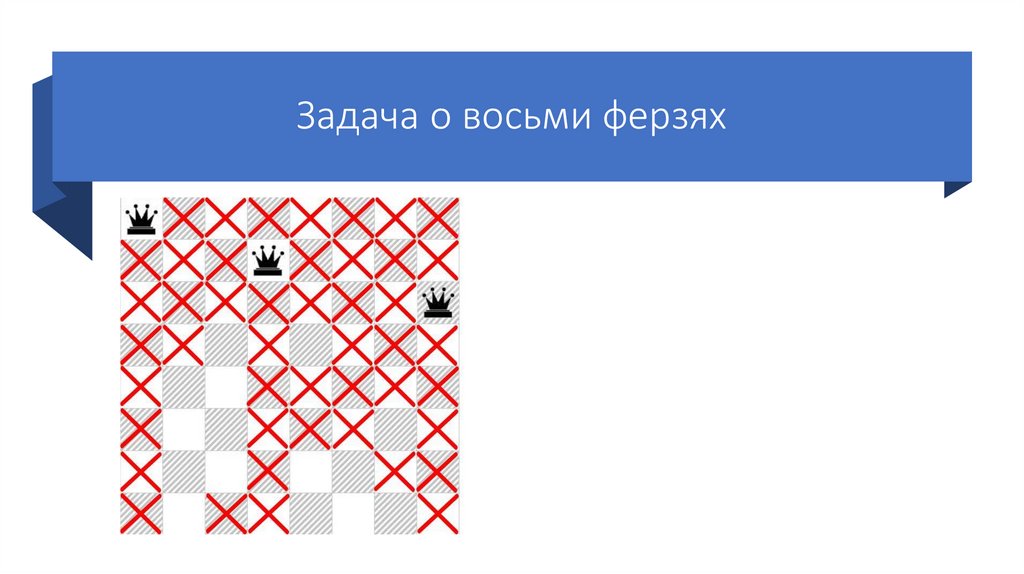
82.
Задача о восьми ферзяхСтавим второго ферзя на
следующую возможную клетку
второй строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
83.
Задача о восьми ферзяхСтавим третьего ферзя на первую
возможную клетку третьей строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
84.
Задача о восьми ферзяхСтавим четвертого ферзя на
первую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
85.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
86.
Задача о восьми ферзяхСтавим пятого ферзя на
следующую возможную клетку
пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя тоже ставить некуда,
поэтому переставляем 4 ферзя.
87.
Задача о восьми ферзяхСтавим четвертого ферзя на
следующую возможную клетку
четвертой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
88.
Задача о восьми ферзяхСтавим пятого ферзя на первую
возможную клетку пятой строки.
Так же отмечаем крестиками
позиции, которые он «бьет».
Так как шестого ферзя поставить
некуда, возвращаемся на шаг
назад (переставляем предыдущего
ферзя на следующую возможную
клетку своей строки).
Но 5 ферзя тоже некуда
переставить, поэтому перемещаем
4 ферзя.
89.
Задача о восьми ферзях90.
Задача о восьми ферзях91.
Задача о восьми ферзях92.
Задача о восьми ферзях93.
Задача о восьми ферзях94.
Задача о восьми ферзях95.
Задача о восьми ферзях96.
Задача о восьми ферзях97.
Задача о восьми ферзях98.
Задача о восьми ферзях99.
Задача о восьми ферзях100.
Задача о восьми ферзях101.
Задача о восьми ферзях102.
Задача о восьми ферзях103.
Задача о восьми ферзях104.
Задача о восьми ферзях105.
Задача о восьми ферзях106.
Задача о восьми ферзях107.
Задача о восьми ферзях108.
Задача о восьми ферзях109.
Задача о восьми ферзях110.
Задача о восьми ферзях111.
Задача о восьми ферзях112.
Задача о восьми ферзях113.
Задача о восьми ферзях114.
Задача о восьми ферзях115.
Задача о восьми ферзях116.
Задача о восьми ферзях117.
Задача о восьми ферзях118.
Задача о восьми ферзях119.
Задача о восьми ферзяхАлгоритм решения:
1. Необходимо реализовать две функции: поставить ферзя и убрать ферзя. Первая
будет ставить в заданную клетку ферзя, а во все остальные отмечать, что они
находятся под боем. Вторая аналогично будет убирать ферзя и клетки шахматной
доски, находящиеся под боем.
2. Помимо этого должна быть функция, которая выбирает, куда поставить ферзей,
она поочередно проходит строки и ставит ферзей так, чтобы они находились не
под боем(ферзи не должны находиться в одной строке, в одном столбце и на
одной диагонали). Но если на какой-то строке функция уже не может поставить
ферзя, то она возвращается на шаг назад, убирает предыдущего ферзя и пытается
поставить его на другое место. И так до тех пор, пока все ферзи не займут свои
места.
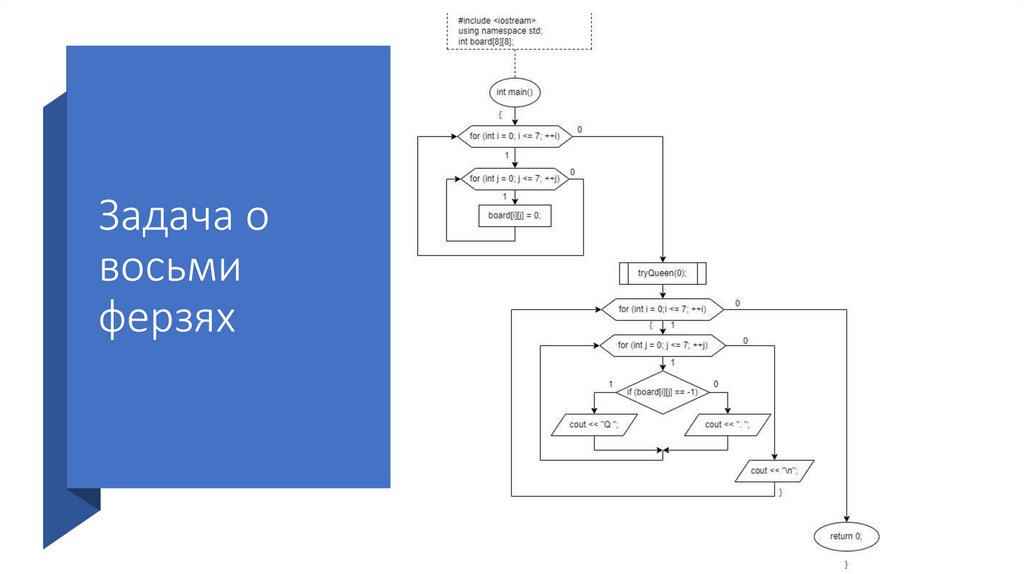
120.
Задача о восьми ферзяхИзначально определен двумерный
массив board, который обозначает
шахматную доску 8 на 8.
В главной функции значение всех
элементов двумерного массива
приравнивается к 0. Вызывается
функция tryQueen, в качестве
параметра передается значение 0 –
первая строка шахматной доски. Когда
отмечены все возможные расстановки
ферзей, выводится схема шахматной
доски, при этом все значения
элементов, равные -1, отмечаются
буквой «Q»(ферзи).
121.
Задача о восьми ферзяхШахматная доска соответствует двумерный
массив размерностью 8 на 8, в котором будут
расставляться ферзи.
Изначально массив board заполнен 0.
Функция setQueen ставит на позицию [i][j]
ферзя и отмечает те позиции, которые данный
ферзь «бьет».
Поставить ферзя – значит
проинициализировать элемент с индексами [i][j] 1. Отметить позиции, которые данный ферзь
«бьет» - значит прибавить 1 к значениям
элементов, которые находятся под «боем».
122.
Задача о восьми ферзяхФункция resetQueen убирает с позиции
[i][j] ферзя и убирает отметки с тех
позиций, которые данный ферзь «бил».
Убрать ферзя – значит
проинициализировать элемент с
индексами [i][j] 0. Отметить позиции,
которые данный ферзь «бил» - значит
отнять 1 от значений элементов, которые
находились под «боем».
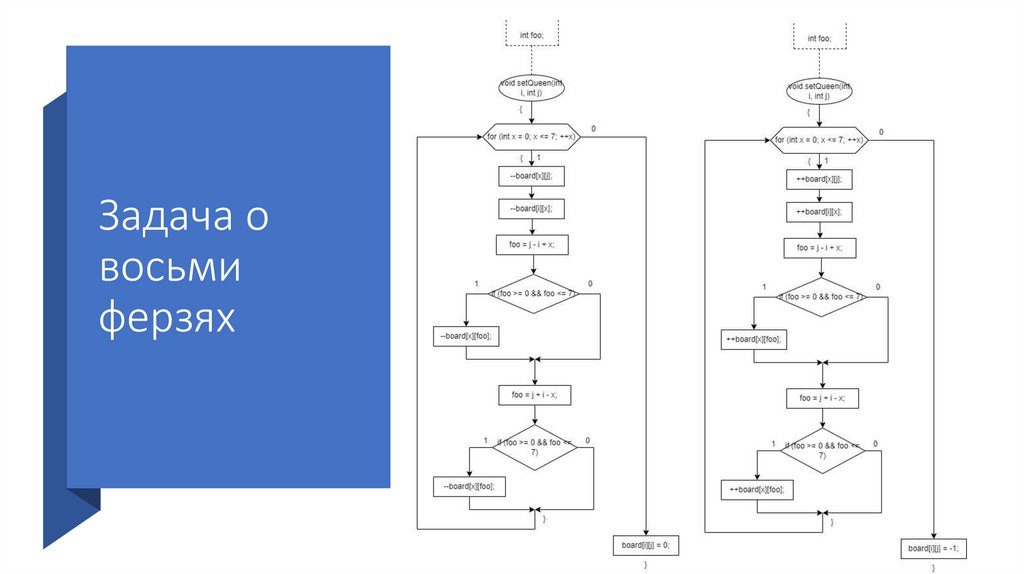
123.
Задача о восьми ферзяхФункция tryQueen проверяет, можно
ли поставить ферзя на данную
позицию.
В цикле for проверяются все
элементы строки; если очередной
элемент равен 0, на данную позицию
ставится ферзь. Далее осуществляется
переход на следующую строчку. Если в
какой-либо из последующих строк ни
в один столбец нельзя поставить
ферзя, осуществляется переход на
предыдущий шаг, и ферзь ставится
уже на следующую допустимую
позицию.
124.
Задача о восьми ферзяхНа скриншоте представлены
результаты постановки первых
двух ферзей
-1 отмечены позиции ферзей;
Положительные числа – позиции,
которые ферзи «бьют».
125.
Задача овосьми
ферзях
126.
Результат работы программы:Задача о
восьми
ферзях
127.
Задача овосьми
ферзях
128.
Задача овосьми
ферзях
129.
Задача овосьми
ферзях




























































































 mathematics
mathematics








