Системы уравнений в ОГЭ

1.

Системы уравнений в ОГЭ
13.02

2.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим соотношение:
Подставив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точки:
От ве т: (0;0), (0,5;0,5)
и

3.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим соотношение:
Подставив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точки:
От ве т: (0;0), (0,5;0,5)
и

4.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
полученное выражение в первое уравне
Вычтем из первого уравнения второе Подставив
и получим соотношение:
Подставив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точк
О т в е т : (0;0), (0,5;0,5)
Таким образом, искомым решением являются точки:
От ве т: (0;0), (0,5;0,5)
и

5.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
Подставив полученное выражение в первое
уравнение
системы, выражение
получаем в первое уравнени
Подставив
полученное
Таким образом, искомым решением являются точк
О т вТаким
е т : (0;0),
(0,5;0,5)
образом,
искомым решением являются точки:
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
От ве т: (0;0), (0,5;0,5)

6.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
ешение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
ычтем Подставив
из первого
уравнения
второе
иуравнение
получим
соотношение:
полученное
выражение
в первое
системы,
получаем в первое уравнени
Подставив
полученное
выражение
одставив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точк
О т вТаким
е т : (0;0),
(0,5;0,5)
образом,
искомым решением являются точки:
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
ве т: (0;0), (0,5;0,5)
акимОтобразом,
искомым решением являются точки:
т : (0;0), (0,5;0,5)
и

7.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
ешение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
ычтем Подставив
из первого
уравнения
второе
иуравнение
получим
соотношение:
полученное
выражение
в первое
системы,
получаем в первое уравнени
Подставив
полученное
выражение
одставив
полученное выражение в первое уравнение системы, получаем
е.
из первого уравнения второе и получим соотношение:
ив полученное выражение в первое уравнение системы, получаем
Таким образом, искомым решением являются точк
О т вТаким
е т : (0;0),
(0,5;0,5)
образом,
искомым решением являются точки:
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
ве т: (0;0), (0,5;0,5)
акимОтобразом,
искомым решением являются точки:
бразом, искомым решением являются точки:
т :(0,5;0,5)
(0;0), (0,5;0,5)
0),
и
и

8.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
ешение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
ычтем Подставив
из первого
уравнения
второе
иуравнение
получим
соотношение:
полученное
выражение
в первое
системы,
получаем в первое уравнени
Подставив
полученное
выражение
одставив
полученное выражение в первое уравнение системы, получаем
е.
из первого уравнения второе и получим соотношение:
ив
полученное
выражение
в первое уравнение системы, получаем
второе
и получим
соотношение:
ение в первое уравнение системы, получаем
Таким образом, искомым решением являются точк
О т вТаким
е т : (0;0),
(0,5;0,5)
образом,
искомым решением являются точки:
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
ве т: (0;0), (0,5;0,5)
акимОтобразом,
искомым решением являются точки:
бразом, искомым решением являются точки:
т :(0,5;0,5)
(0;0), (0,5;0,5)
0),
ением являются точки:
и
и
и

9.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
ешение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
ычтем Подставив
из первого
уравнения
второе
иуравнение
получим
соотношение:
полученное
выражение
в первое
системы,
получаем в первое уравнени
Подставив
полученное
выражение
одставив
полученное выражение в первое уравнение системы, получаем
е.
из первого уравнения второе и получим соотношение:
ив
полученное
выражение
в первое уравнение системы, получаем
второе
и получим
соотношение:
ение в первое уравнение системы, получаем
Таким образом, искомым решением являются точк
О т вТаким
е т : (0;0),
(0,5;0,5)
лучим соотношение:
образом,
искомым решением являются точки:
ое уравнение системы, получаем
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
ве т: (0;0), (0,5;0,5)
акимОтобразом,
искомым решением являются точки:
бразом, искомым решением являются точки:
т :(0,5;0,5)
(0;0), (0,5;0,5)
0),
ением являются точки:
ются точки:
и
и
и
и

10.

21. Решите систему уравнений:
Решение.
Вычтем из первого уравнения второе и получим со
Решение.
Решение.
ешение.
Подставив
полученное выражение в первое уравне
Вычтем из первого уравнения второеВычтем
и получимизсоотношение:
первого уравнения второе и получим соот
ычтем Подставив
из первого
уравнения
второе
иуравнение
получим
соотношение:
полученное
выражение
в первое
системы,
получаем в первое уравнени
Подставив
полученное
выражение
одставив
полученное выражение в первое уравнение системы, получаем
е.
из первого уравнения второе и получим соотношение:
ив
полученное
выражение
в первое уравнение системы, получаем
второе
и получим
соотношение:
ение в Решение.
первое уравнение системы, получаем
образом,
искомым решением являются точк
Вычтем из первого уравнения второе иТаким
получим
соотношение:
вТаким
е т : уравнение
(0;0),
(0,5;0,5)
лучим соотношение:
Подставив полученное выражениеОвтпервое
системы,
получаем
образом,
искомым
решением являются точки:
ое уравнение системы, получаем
Таким образом, искомым решением
точки:
О т вявляются
е т : (0;0),
(0,5;0,5) и
ве т: (0;0), (0,5;0,5)
акимОтобразом,
искомым решением являются точки:
бразом, искомым решением являются точки:
т :(0,5;0,5)
(0;0), (0,5;0,5)
0),
ением являются точки:
и
и
Таким образом, искомым решением являются точки:
ются О
точки:
т в е т : (0;0),и(0,5;0,5)
и
и

11.

№22. Из пункта А в пункт В, расположенный ниже по
течению реки, отправился плот. Одновременно навстречу
ему из пункта В вышел катер. Встретив плот, катер сразу
повернул и поплыл назад. Какую часть пути от А до В
пройдет плот к моменту возвращения катера в пункт В, если
скорость катера в стоячей воде вчетверо больше скорости
течения реки?
Обозначим следующие значения за переменные:
Скорость реки – x
Скорость катера в стоячей воде – 4x
Расстояние от А до В места встречи – S1
Расстояние, которое пройдет плот – S2
Расстояние от А до В – 1
К месту встречи катер и плот ехали одинаковое количество времени. Тогда:

12.

№22. Из пункта А в пункт В, расположенный ниже по
течению реки, отправился плот. Одновременно навстречу
ему из пункта В вышел катер. Встретив плот, катер сразу
повернул и поплыл назад. Какую часть пути от А до В
пройдет плот к моменту возвращения катера в пункт В, если
скорость катера в стоячей воде вчетверо больше скорости
течения реки?
Обозначим следующие значения за переменные:
Скорость реки – x
Скорость катера в стоячей воде – 4x
Расстояние от А до В места встречи – S1
Расстояние, которое пройдет плот – S2
Расстояние от А до В – 1

13.

№22. Из пункта А в пункт В, расположенный ниже по
течению реки, отправился плот. Одновременно навстречу
ему из пункта В вышел катер. Встретив плот, катер сразу
повернул и поплыл назад. Какую часть пути от А до В
пройдет плот к моменту возвращения катера в пункт В, если
скорость катера в стоячей воде вчетверо больше скорости
течения реки?
Обозначим следующие значения за переменные:
Скорость реки – x
Скорость катера в стоячей воде – 4x
Расстояние от А до В места встречи – S1
Расстояние, которое пройдет плот – S2
Расстояние от А до В – 1
К месту встречи катер и плот ехали одинаковое количество времени. Тогда:

14.

№22. Из пункта А в пункт В, расположенный ниже по
течению реки, отправился плот. Одновременно навстречу
ему из пункта В вышел катер. Встретив плот, катер сразу
повернул и поплыл назад. Какую часть пути от А до В
пройдет плот к моменту возвращения катера в пункт В, если
скорость катера в стоячей воде вчетверо больше скорости
течения реки?
Обозначим следующие значения за переменные:
Скорость реки – x
Скорость катера в стоячей воде – 4x
Расстояние от А до В места встречи – S1
Расстояние, которое пройдет плот – S2
Расстояние от А до В – 1
К месту встречи катер и плот ехали одинаковое количество времени. Тогда:

15.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

16.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

17.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

18.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

19.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

20.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

21.

Обратно катер и плот ехали одинаковое время. Тогда катер
за это время преодолел (1 – S1), а плот преодолел расстояние
S2. Тогда выразим время через эти выражения

22.

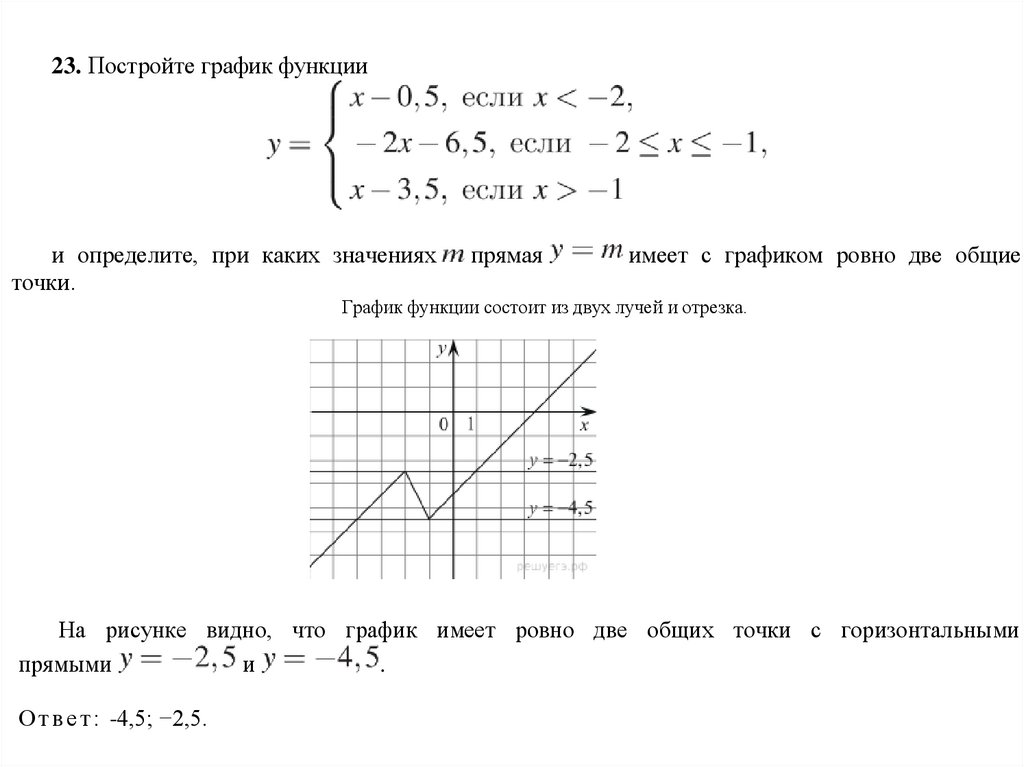
23. Постройте график функции
и определите, при каких значениях
точки.
прямая
имеет с графиком ровно две общие
График функции состоит из двух лучей и отрезка.
На рисунке видно, что график имеет ровно две общих точки с горизонтальными
прямыми
и
.
О т в е т : -4,5; −2,5.

23.

22. Первая труба пропускает на 2 литра воды в минуту
меньше, чем вторая. Сколько литров воды в минуту
пропускает вторая труба, если резервуар объёмом 130
литров она заполняет на 4 минуты быстрее, чем первая
труба заполняет резервуар объёмом 136 литров?
Решение.
Пусть вторая труба пропускает
пропускает
литра в минуту.
литров воды в минуту,
Составим таблицу по данным задачи:
Производительность
Время (мин) Объём работ (л)
(л/мин)
Первая труба
136
Вторая труба
130
, тогда первая труба

24.

Составим таблицу по данным задачи:
Производительность
Время (мин) Объём работ (л)
(л/мин)
Первая труба
136
Вторая труба
130
Так как вторая труба заполнила резервуар на 4 минуты быстрее, получаем уравнение:
Решим уравнение:
или
Отбрасывая постороннее решение −6,5, получаем, что вторая труба пропускает 10 литров в
минуту.
О т в е т : 10.

25.

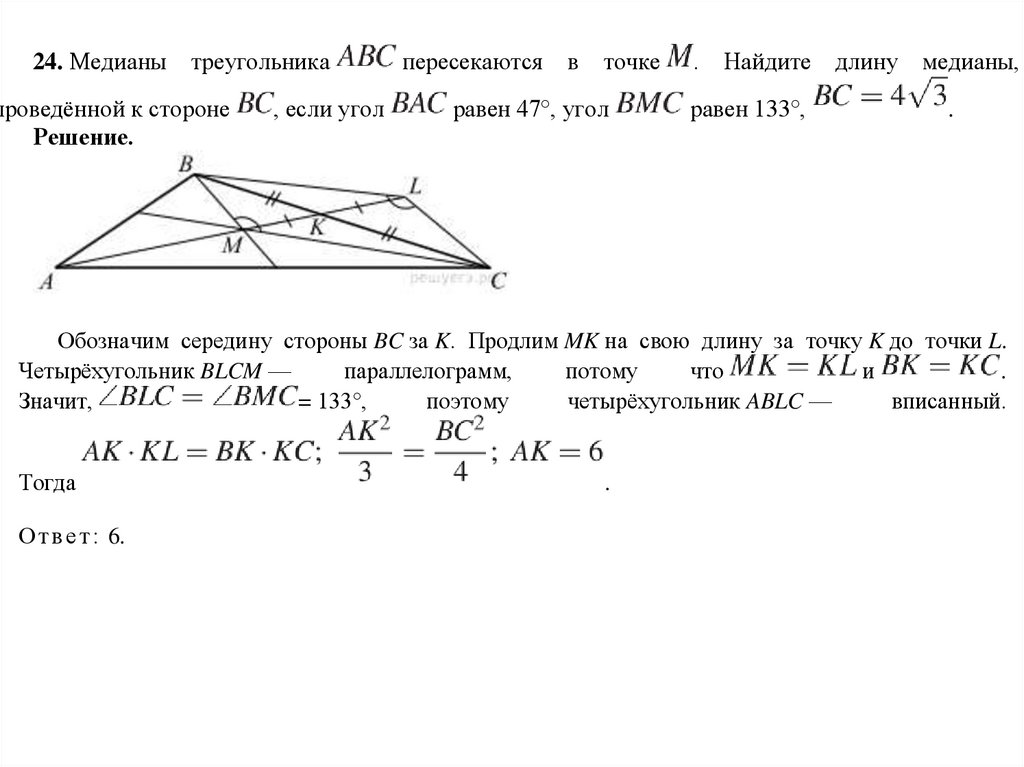
24. Медианы треугольника
проведённой к стороне
Решение.
, если угол
пересекаются
в точке
равен 47°, угол
.
Найдите длину медианы,
равен 133°,
.
Обозначим середину стороны BC за K. Продлим MK на свою длину за точку K до точки L.
Четырёхугольник BLCM —
параллелограмм,
потому
что
и
.
Значит,
= 133°,
поэтому
четырёхугольник ABLC —
вписанный.
Тогда
О т в е т : 6.
.

26.

№ 23

27.

28.

№ 25

29.

25. В параллелограмме ABCD проведены
высоты BH и BE к сторонам AD и CD
соответственно, при этом BH = BE. Докажите,
что ABCD — ромб.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой
стороне.
Тогда, с одной стороны, S = AD · BH, а с другой стороны, S = CD · BE. Поскольку BH = BE ,
получаем, что AD = CD. Следовательно, все стороны параллелограмма равны, а значит, ABCD —
ромб.