Асимптоты

1. Асимптоты

2. МНЕ В ТЕБЕ НРАВИТСЯ…..

3.

Дайте определение предела функции в точке.
Поясните смысл этого определения.
Как вы понимаете предела функции в точке.
Как вы понимаете предела функции на
бесконечности.
Что такое односторонний предел функции в точке?

4. НАУЧИМСЯ

находить вертикальную асимптоту;
выделять целую часть (выполняет деление
многочленов с остатком);
находить наклонную асимптоту;
использовать условие для нахождения наклонной
асимптоты;
составлять уравнения асимптот

5. Вертикальная асимптота

Это прямая вида x = a при условии существования
предела
.
Как правило, при определении вертикальной
асимптоты ищут не один предел, а два односторонних
(левый и правый). Это делается с целью определить,
как функция ведёт себя по мере приближения к
вертикальной асимптоте с разных сторон. Например:
1.)
2.)
Замечание: обратите внимание на знаки
бесконечностей в этих равенствах.

6. Нахождение вертикальных асимптот

Из определения асимптоты следует, что прямая х = а –
асимптота кривой y = f(x).
Например, для функции f(x) = 2/(x – 5) прямая х = 5
является вертикальной асимптотой.
У функции
прямые х = 3 и х = -3
являются вертикальными асимптотами кривой.
Вертикальных асимптот график не имеет, если область
определения не имеет граничных точек. (У графиков
многочленов не бывает вертикальных асимптот.)
Например, f(x) = 2x³ - 3x² + x + 5 не имеет
вертикальных асимптот.

7. Вертикальные асимптоты

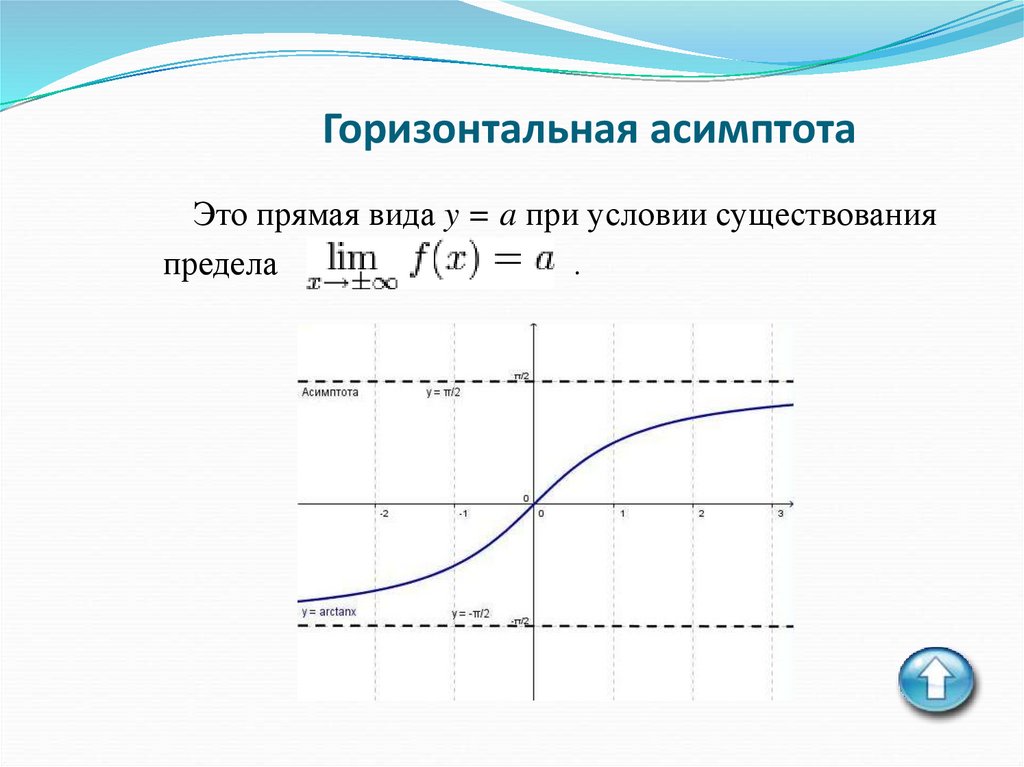
8. Горизонтальная асимптота

Это прямая вида y = a при условии существования
предела
.

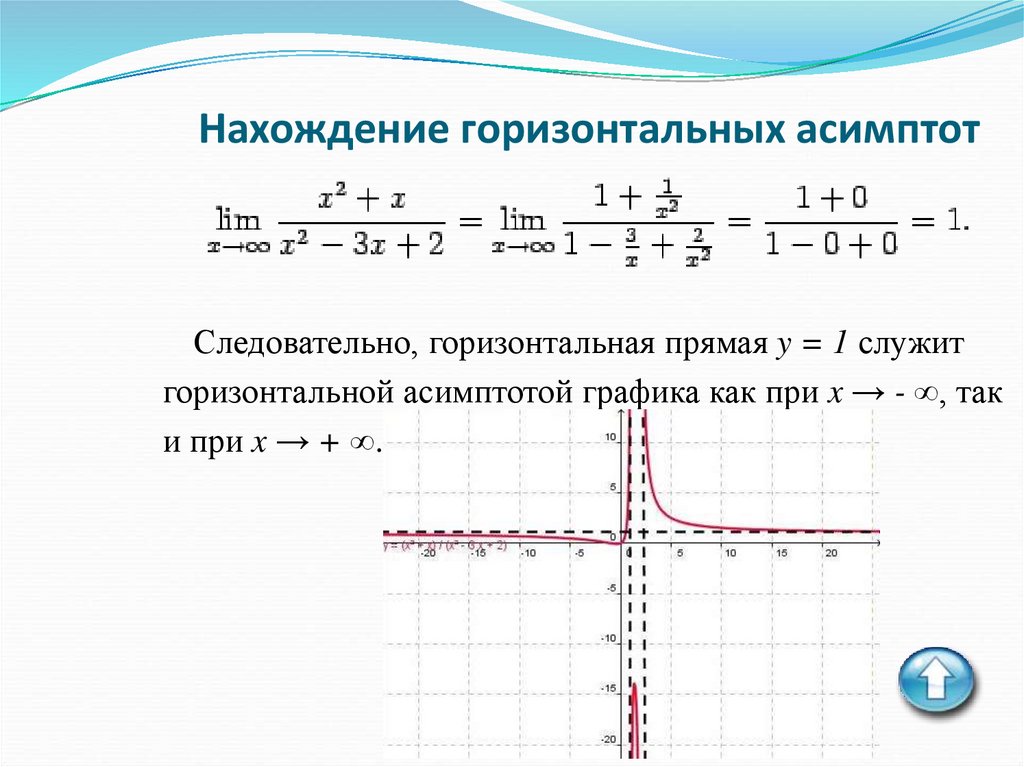
9. Нахождение горизонтальных асимптот

Следовательно, горизонтальная прямая y = 1 служит
горизонтальной асимптотой графика как при x → - ∞, так
и при x → + ∞.

10. Наклонная асимптота

Это прямая вида y = kx + b при условии
существования пределов:
1.)
2.)
Замечание: функция может иметь не более двух
наклонных (горизонтальных) асимптот!
Замечание: Если хотя бы один из двух упомянутых
выше пределов не существует (т.е. равен ∞), то
наклонной асимптоты при x → + ∞ (или x → - ∞) не
существует!

11. Порядок нахождения асимптот

2.
Нахождение вертикальных асимптот;
Нахождение горизонтальных асимптот;
3.
Нахождение двух пределов
4.
Нахождение двух пределов
1.
;
.

12. Нахождение наклонных асимптот

Находятся по формуле:
где
.
Также наклонную асимптоту можно найти, выделив
целую часть.

13. Выделение целой части у наклонных асимптот

Например, дана функция
Разделив нацело числитель на знаменатель,
получим:
При x → ∞,
,
то есть:
,
и y = 2x + 5
является искомым уравнением асимптоты
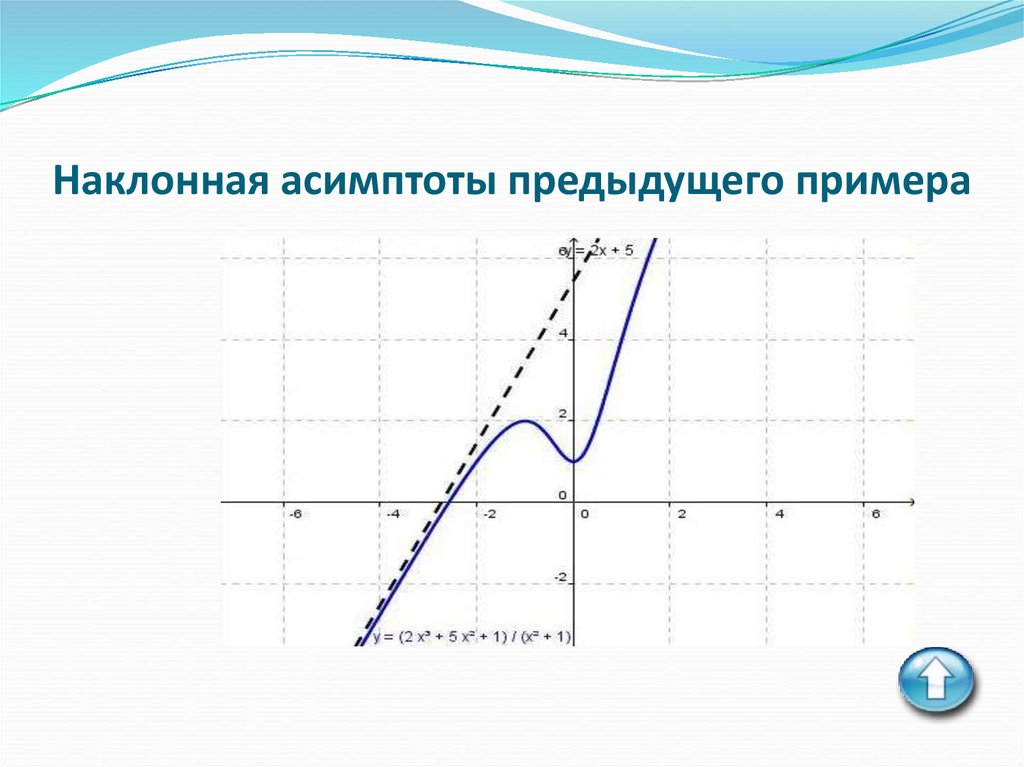
Наклонная асимптоты предыдущего примера

14. Наклонная асимптоты предыдущего примера

15.

Пример 1. Для функции
найти асимптоты.
Пример 2. Найти асимптоты графика функции:

16. Рефлексия

- Какие затруднения у вас возникли при работе на
уроке?
- Какие знания у вас были крепкими?

17. Домашнее задание

Просмотреть
https://youtu.be/QL85fMKF9dA
Рассмотреть решение примера 10 стр 165
Выполнить : №6.8