Асимптоты графика функции

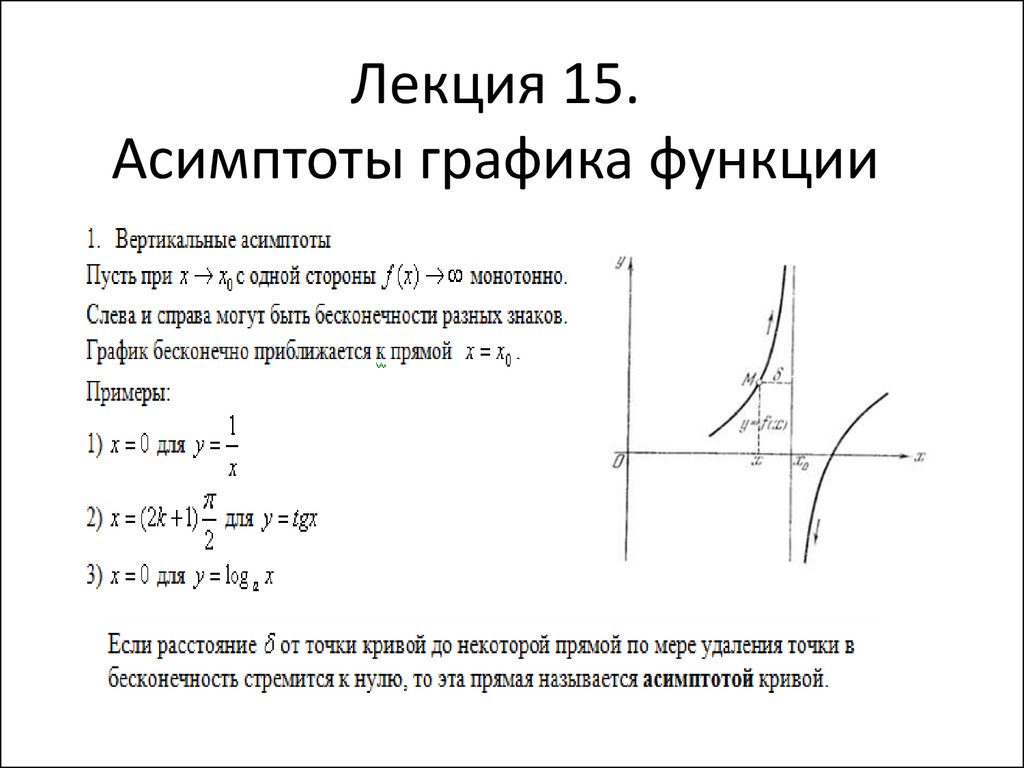
1. Лекция 15. Асимптоты графика функции

2. 2. Горизонтальные асимптоты

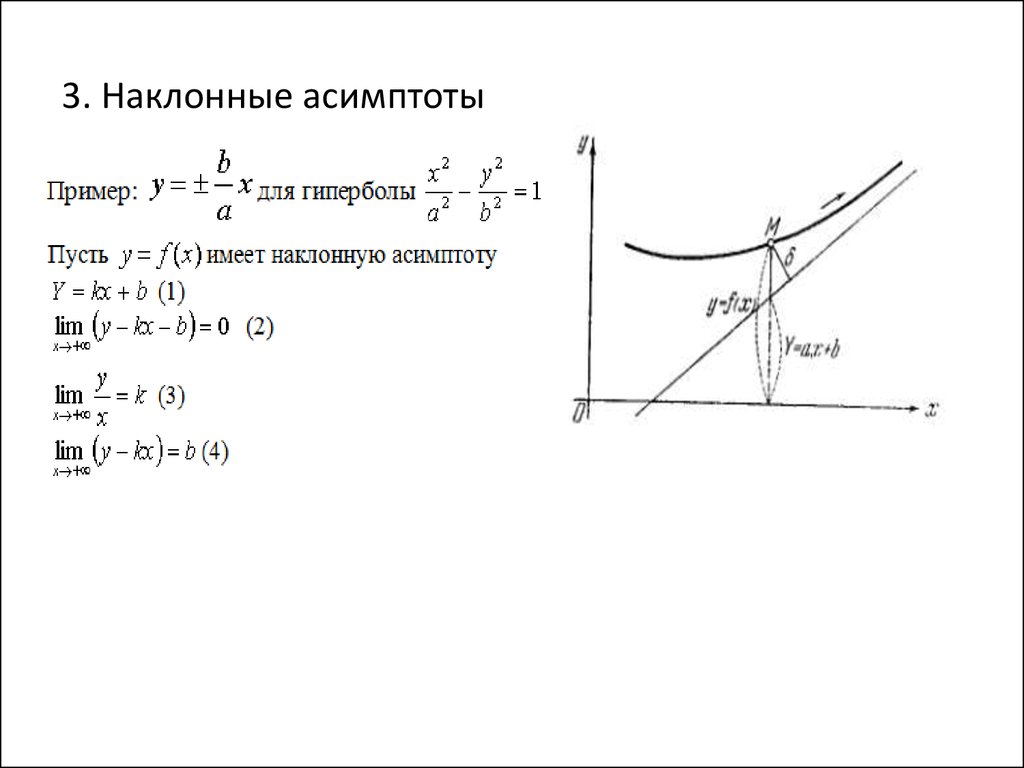
3. 3. Наклонные асимптоты

4.

• ТЕОРЕМА 38. Для того чтобы график
функции у=f(x) имел при х + наклонную
асимптоту Y=kx+b необходимо и
достаточно, чтобы существовали пределы
lim x
f ( x)
k , lim x f ( x) kx b.
x
Пример
2 x2 x
y
x 1

5.

• Для дробно рациональной функции:
• Асимптоты на + и одновременно существуют
или не существуют и в первом случае совпадают.
• Если степень знаменателя выше степени числителя,
то асимптота нулевая.
• Если степень знаменателя равна степени
числителя, то асимптота горизонтальная.
• Если степень знаменателя на 1 ниже степени
числителя, то существует наклонная асимптота.
• Если разность степеней больше 1, то наклонных
асимптот не существует.

6. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ

1. Элементарное исследование
- область определения, непрерывность,
точки разрыва, их тип (вертикальные
асимптоты);
- четность, периодичность
- точки пересечения с осями;
- наклонные асимптоты;
- точки пересечения с асимптотами

7.

2. Промежутки возрастания, убывания, точки
экстремума.
3. Промежутки выпуклости, вогнутости, точки
перегиба.
Пример.
2 x3 5 x 2 14 x 6
y
4 x2