Основы алгебры логики

1. Основы алгебры логики

1
Основы алгебры
логики
• Логические операции
• Логические выражения
• Упрощение логических выражений
• Логические уравнения
• Синтез логических выражений
• Множества и логика
• Предикаты и кванторы
• Логические элементы компьютера
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

2. Основы алгебры логики

2
Основы алгебры
логики
Логические операции
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

3. Вспомним известное…

Основы алгебры логики, 10 класс
3
Вспомним известное…
Логическое высказывание – это
повествовательное предложение,
относительно которого можно однозначно
сказать, истинно оно (0) или ложно (1).
Алгебра логики (булева алгебра) — это
математический аппарат, с помощью которого
записывают, вычисляют, упрощают и
преобразуют логические высказывания.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

4. Операция НЕ (инверсия)

Основы алгебры логики, 10 класс
4
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
также A , A ,
А
не А
0
1
1
0
not A (Python),
! A (С++)
таблица
истинности
операции НЕ
Таблица истинности логической операции – это
таблица, где в левой части записываются все
возможные комбинации значений исходных данных,
а в правой – результат этой операции для каждой
комбинации.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

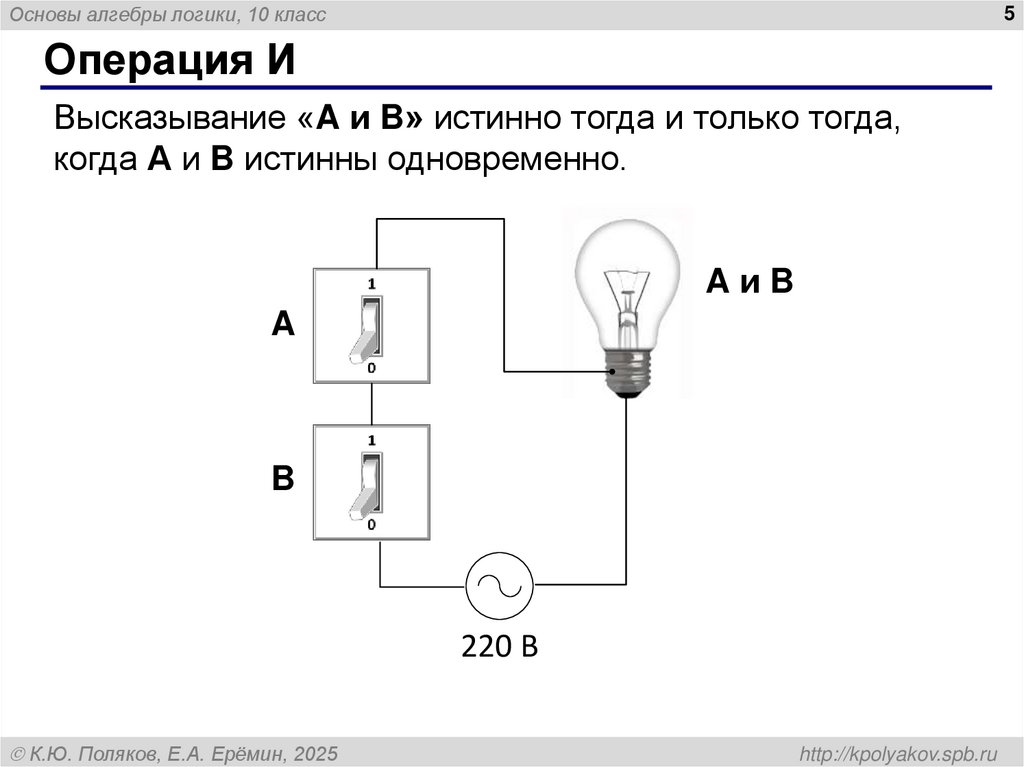
5. Операция И

Основы алгебры логики, 10 класс
5
Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

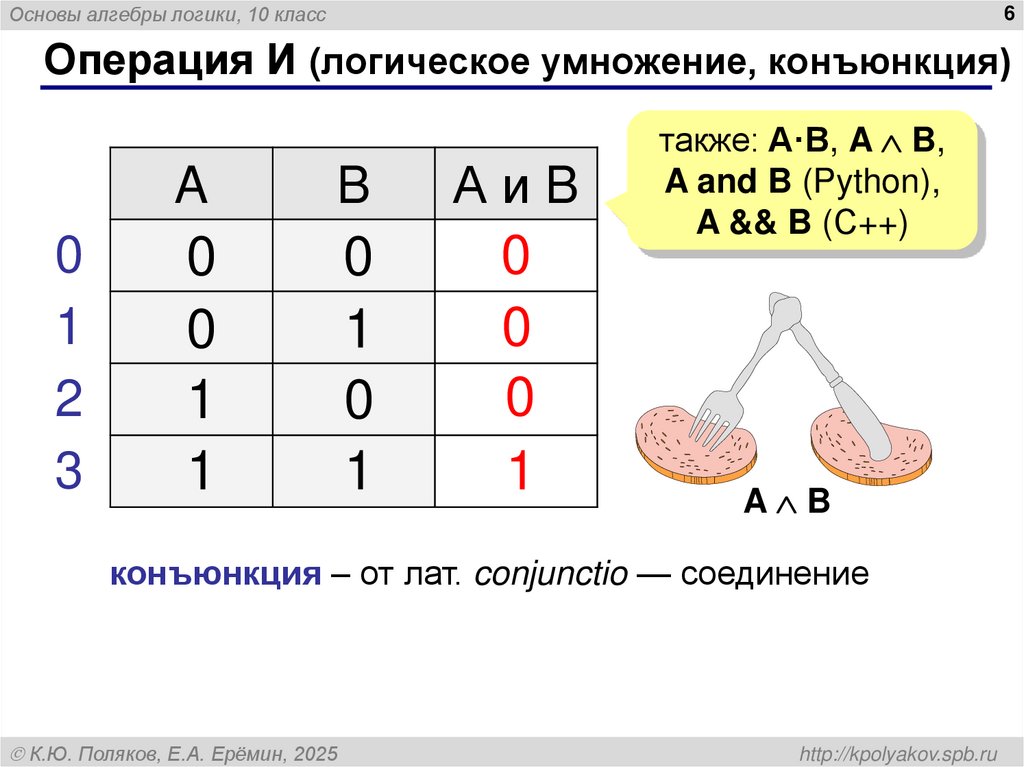
6. Операция И (логическое умножение, конъюнкция)

Основы алгебры логики, 10 класс
6
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также: A·B, A B,
A and B (Python),
A && B (С++)
A B
конъюнкция – от лат. conjunctio — соединение
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

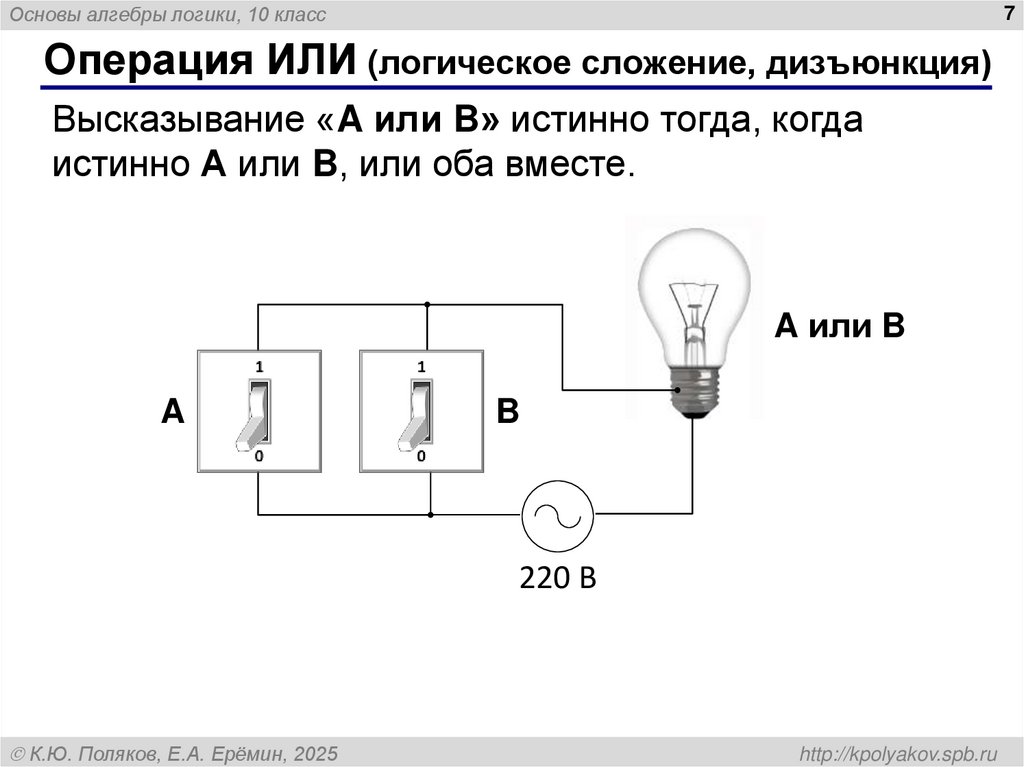
7. Операция ИЛИ (логическое сложение, дизъюнкция)

Основы алгебры логики, 10 класс
7
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
истинно А или B, или оба вместе.
A или B
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

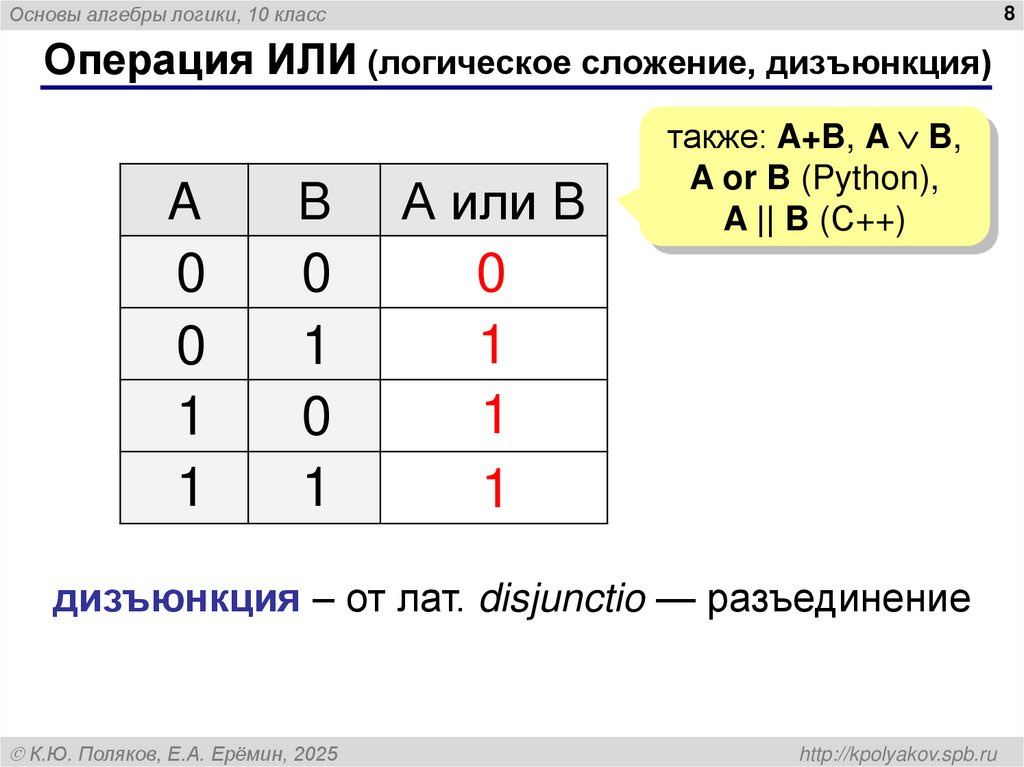
8. Операция ИЛИ (логическое сложение, дизъюнкция)

Основы алгебры логики, 10 класс
8
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Python),
A || B (С++)
дизъюнкция – от лат. disjunctio — разъединение
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

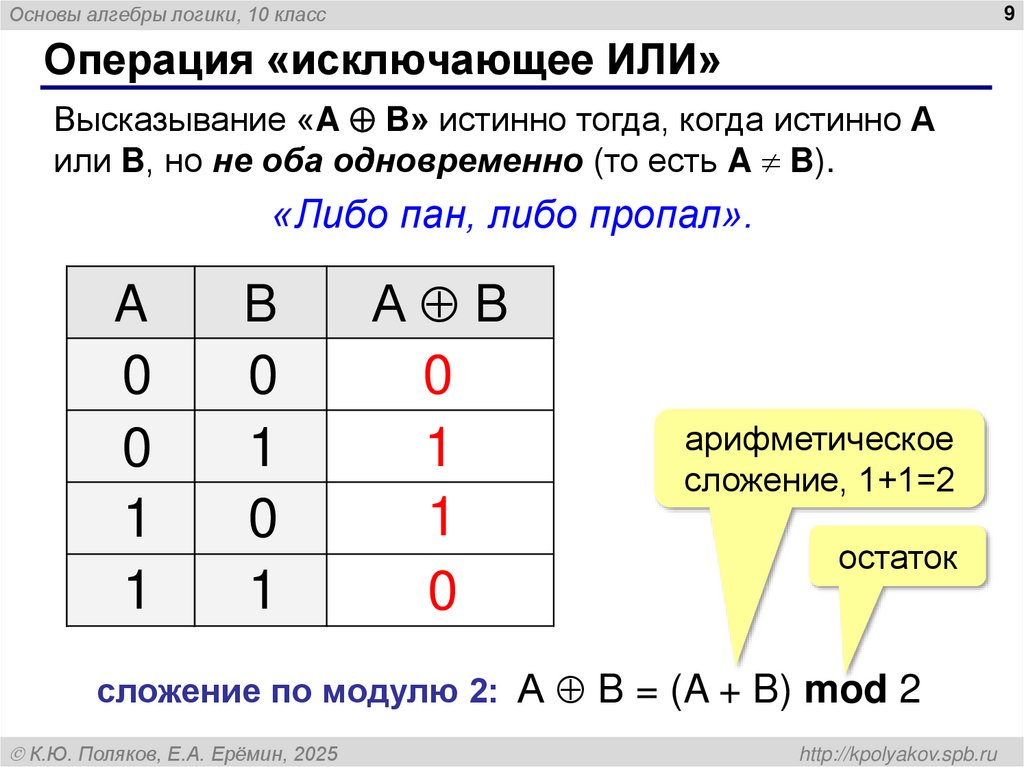
9. Операция «исключающее ИЛИ»

Основы алгебры логики, 10 класс
9
Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (то есть A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

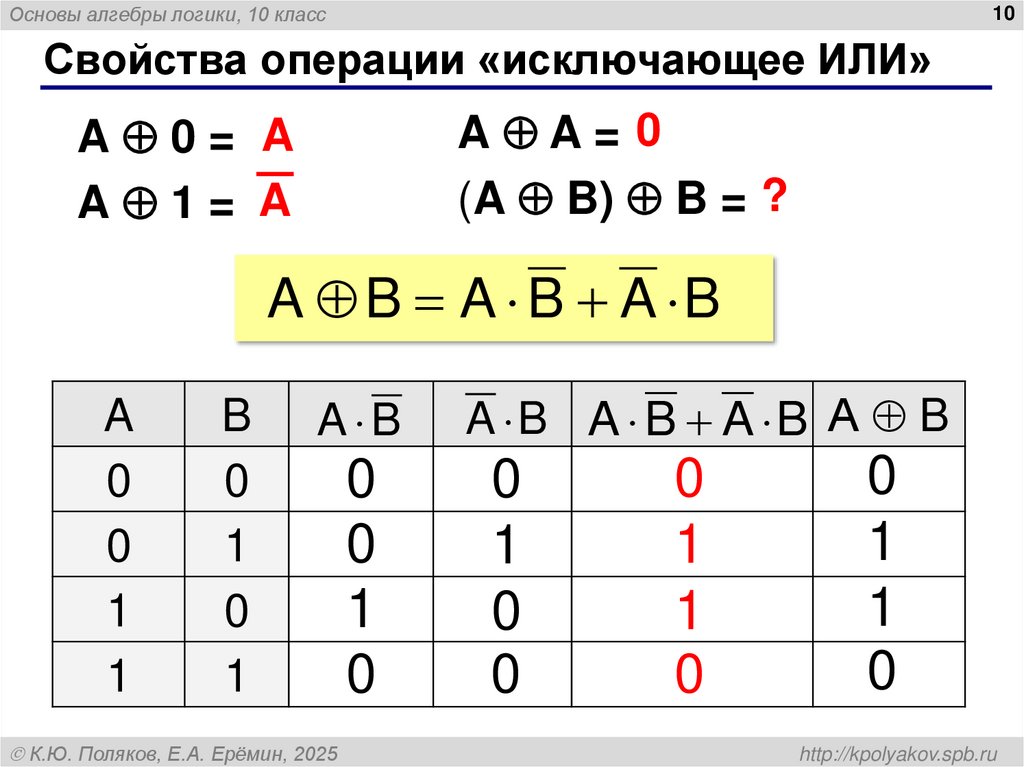
10. Свойства операции «исключающее ИЛИ»

Основы алгебры логики, 10 класс
10
Свойства операции «исключающее ИЛИ»
A A= 0
(A B) B = ?
A 0= A
A 1= A
A B A B A B
A
0
0
1
1
B
0
1
0
1
A B
A B A B A B А B
0
0
1
0
0
1
0
0
К.Ю. Поляков, Е.А. Ерёмин, 2025
0
1
1
0
0
1
1
0
http://kpolyakov.spb.ru

11. Импликация («если …, то …»)

Основы алгебры логики, 10 класс
11
Импликация («если …, то …»)
Высказывание «A B» истинно, если не
исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2025
А B
1
1
0
1
A B A B
http://kpolyakov.spb.ru

12. Импликация («если …, то …»)

Основы алгебры логики, 10 класс
12
Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит дома».
A – «Вася идет гулять».
A
B
А
B
B – «Маша сидит дома».
A B 1
? А если Вася не идет
гулять?
0
0
1
1
0
1
0
1
1
1
0
1
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

13. Эквиваленция («тогда и только тогда, …»)

Основы алгебры логики, 10 класс
13
Эквиваленция («тогда и только тогда, …»)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
A B A B A B A B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

14. Базовый набор операций

Основы алгебры логики, 10 класс
14
Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно
реализовать любую логическую операцию.
И
ИЛИ
НЕ
базовый набор операций
? Сколько всего существует логических операций с
двумя переменными?
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

15. Что такое логическая функция?

Основы алгебры логики, 10 класс
15
Что такое логическая функция?
Логическая функция — это правило
преобразования входных логических значений
в выходные. Логическая функция задаётся
таблицей истинности.
Выражения:
A
A+A B
A (A+B)
A
0
0
1
1
B
0
1
0
1
F
0
0
1
1
функция
? Сколько можно записать выражений?
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

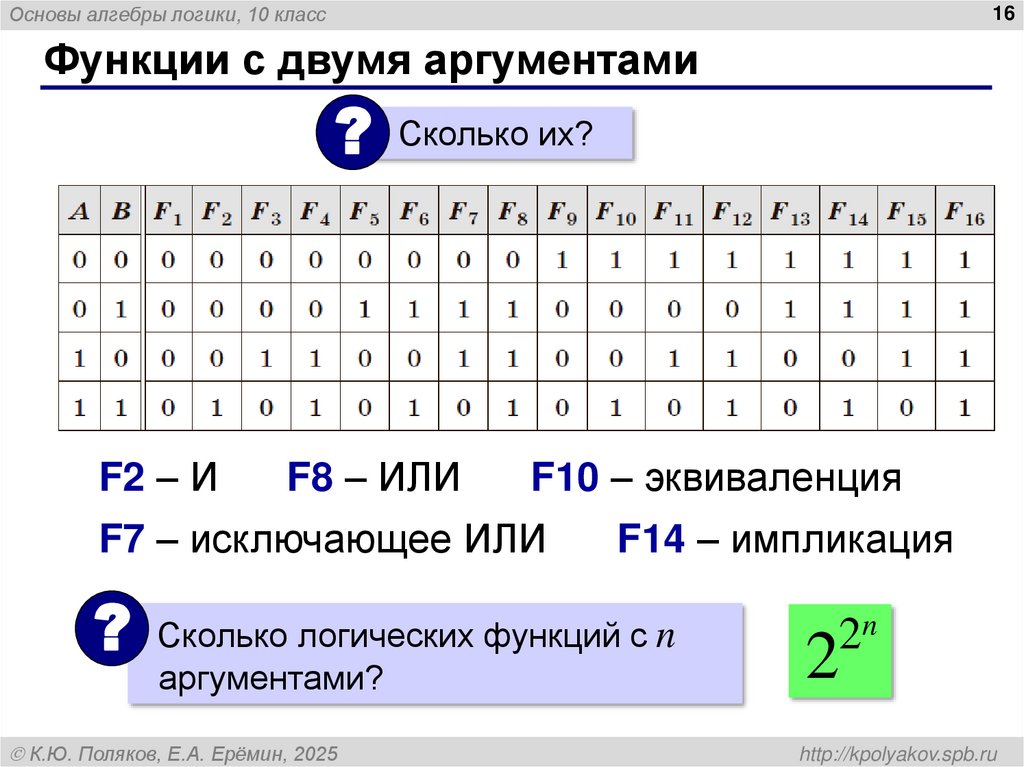
16. Функции с двумя аргументами

Основы алгебры логики, 10 класс
16
Функции с двумя аргументами
? Сколько их?
F2 – И
F8 – ИЛИ
F10 – эквиваленция
F7 – исключающее ИЛИ
F14 – импликация
? Сколько логических функций с n
аргументами?
К.Ю. Поляков, Е.А. Ерёмин, 2025
2n
2
http://kpolyakov.spb.ru

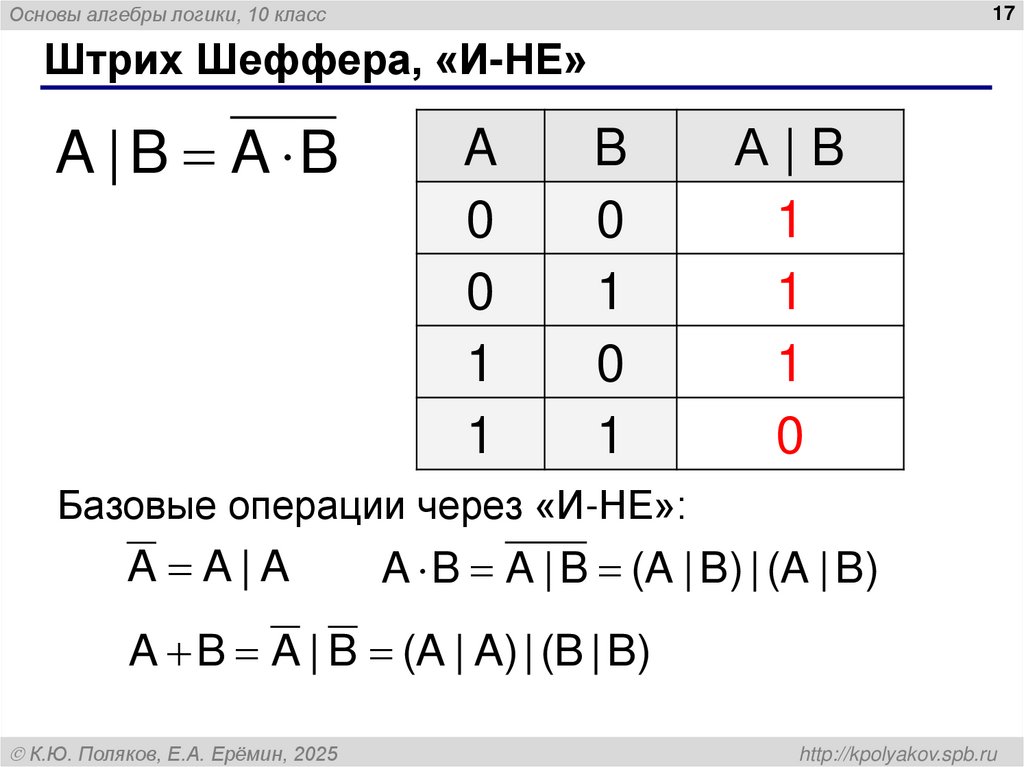
17. Штрих Шеффера, «И-НЕ»

Основы алгебры логики, 10 класс
17
Штрих Шеффера, «И-НЕ»
A | B A B
A
0
0
1
1
B
0
1
0
1
А|B
1
1
1
0
Базовые операции через «И-НЕ»:
A A|A
A B A | B (A | B) | (A | B)
A B A | B (A | A) | (B | B)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

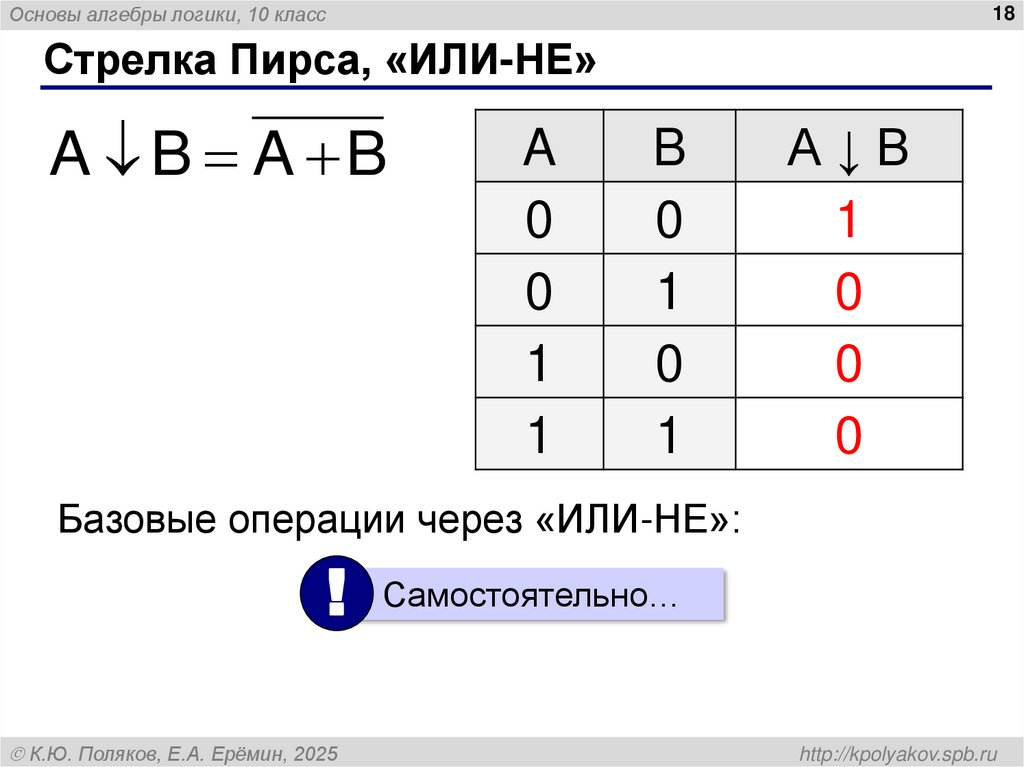
18. Стрелка Пирса, «ИЛИ-НЕ»

Основы алгебры логики, 10 класс
18
Стрелка Пирса, «ИЛИ-НЕ»
A B A B
A
0
0
1
1
B
0
1
0
1
А↓B
1
0
0
0
Базовые операции через «ИЛИ-НЕ»:
! Самостоятельно…
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

19. Основы алгебры логики

19
Основы алгебры
логики
Логические выражения
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

20. Вспомним известное…

Основы алгебры логики, 10 класс
20
Вспомним известное…
Логическое выражение — это символическая
запись высказывания, которая может
содержать логические переменные и знаки
логических операций.
Выражения:
A
A+A B
A (A+B)
К.Ю. Поляков, Е.А. Ерёмин, 2025
A
0
0
1
1
B
0
1
0
1
F
0
0
1
1
функция
http://kpolyakov.spb.ru

21. Как строятся логические выражения?

Основы алгебры логики, 10 класс
21
Как строятся логические выражения?
Прибор имеет три датчика и может работать, если два из
них исправны. Записать в виде формулы ситуацию
«авария».
A – «Датчик № 1 неисправен».
B – «Датчик № 2 неисправен».
Формализация – это
переход к записи на
C – «Датчик № 3 неисправен».
формальном языке!
Аварийный сигнал:
X – «Неисправны два датчика».
X – «Неисправны датчики № 1 и № 2» или
«Неисправны датчики № 1 и № 3» или
«Неисправны датчики № 2 и № 3».
логическая
формула
X A B A C B C
!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

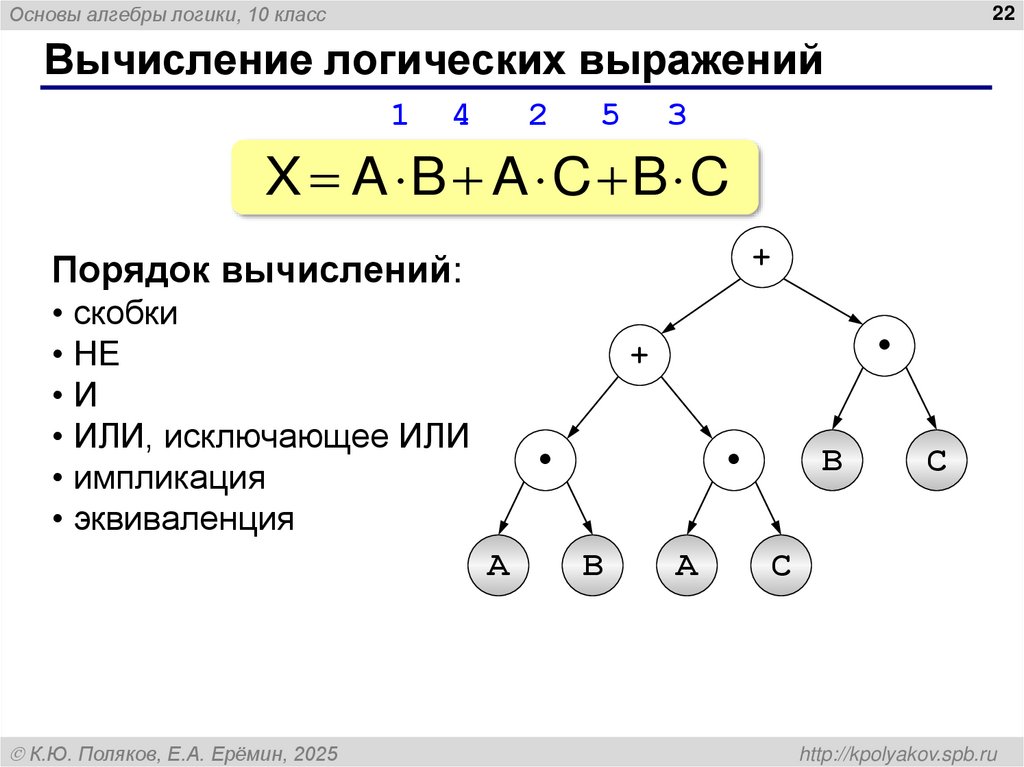
22. Вычисление логических выражений

Основы алгебры логики, 10 класс
22
Вычисление логических выражений
1
4
2
5
3
X A B A C B C
+
Порядок вычислений:
• скобки
• НЕ
•И
• ИЛИ, исключающее ИЛИ
• импликация
• эквиваленция
A
К.Ю. Поляков, Е.А. Ерёмин, 2025
+
B
A
B
C
С
http://kpolyakov.spb.ru

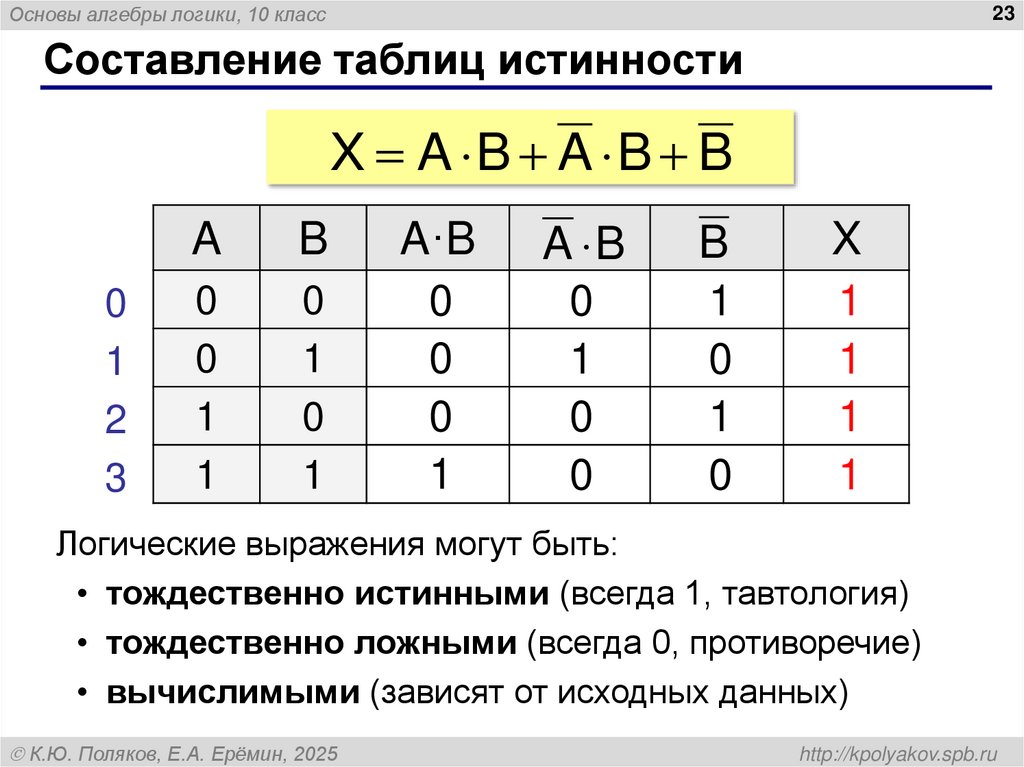
23. Составление таблиц истинности

Основы алгебры логики, 10 класс
23
Составление таблиц истинности
X A B A B B
0
1
2
3
A
B
A·B
A B
B
X
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
1
1
Логические выражения могут быть:
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

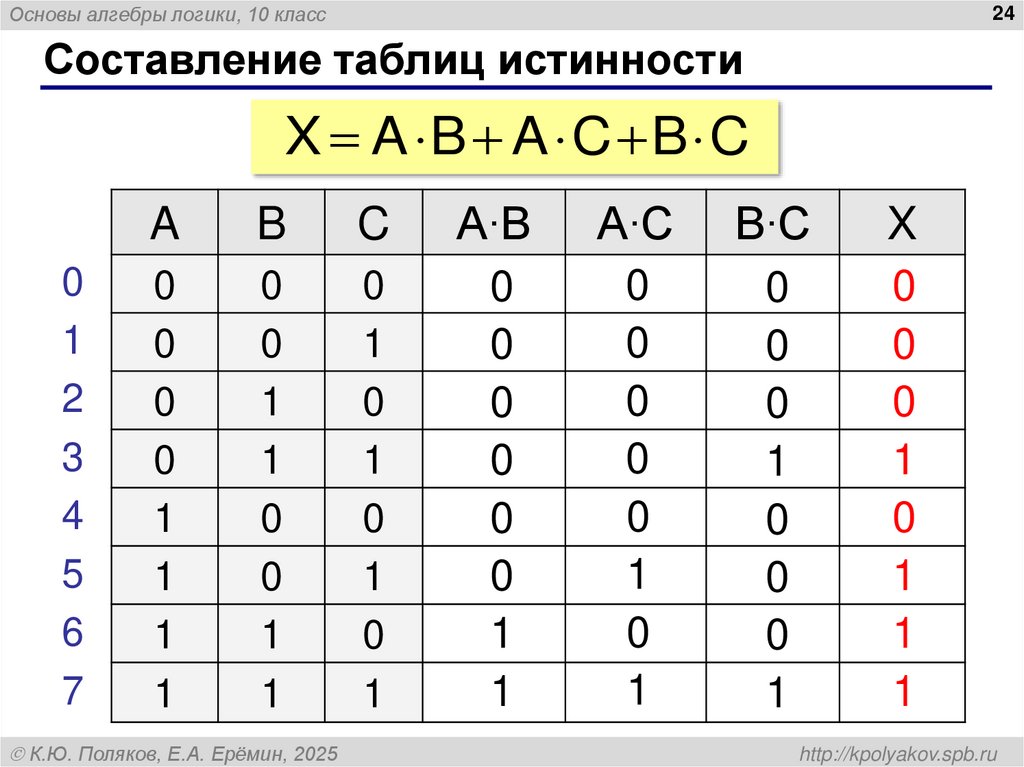
24. Составление таблиц истинности

Основы алгебры логики, 10 класс
24
Составление таблиц истинности
X A B A C B C
0
1
2
3
4
5
6
7
A
B
C
A∙B
A∙C
B∙C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

25. Задачи

Основы алгебры логики, 10 класс
25
Задачи
Задача 1. При каких значениях логических переменных
истинно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все сомножители равны 1:
X 1 X 4 1,
X2 X3 X5 0
Задача 2. При каких значениях логических переменных
ложно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все слагаемые равны 0:
X 1 X 3 X 5 0,
К.Ю. Поляков, Е.А. Ерёмин, 2025
X2 X4 1
http://kpolyakov.spb.ru

26. Задачи

Основы алгебры логики, 10 класс
26
Задачи
Задача 3. Запишите любое логические выражение,
соответствующее таблице истинности:
в полной
23 = 8 строк
X Y Z F
Полная таблица?
?
1 0 0 1
0 0 0 0
1 1 1 0
К.Ю. Поляков, Е.А. Ерёмин, 2025
истинно при X = 1, Y = Z = 0
X Y Z 1
F X Y Z
http://kpolyakov.spb.ru

27. Задачи

Основы алгебры логики, 10 класс
27
Задачи
Задача 4. Запишите любое логические выражение,
соответствующее таблице истинности:
X
1
0
1
Y
0
0
1
Z
0
0
1
F
0
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2025
ложно при X = 1, Y = Z = 0
X Y Z 0
F X Y Z
http://kpolyakov.spb.ru

28. Задачи

Основы алгебры логики, 10 класс
28
Задачи
Задача 5. Символом F обозначено одно
из указанных ниже логических
выражений от трёх аргументов: X, Y, Z.
Дан фрагмент таблицы истинности
выражения F. Какое выражение
соответствует F?
1) X Y Z
1) ¬X ¬Y ¬Z
2) X Y Z
2) X Y Z
3) X Y Z
3) X Y Z
4) X Y Z
4) ¬X ¬Y ¬Z
X Y
1 0
0 0
1 1
Z
0
0
1
F
1
1
0
Быстрый способ:
F X Y Z
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

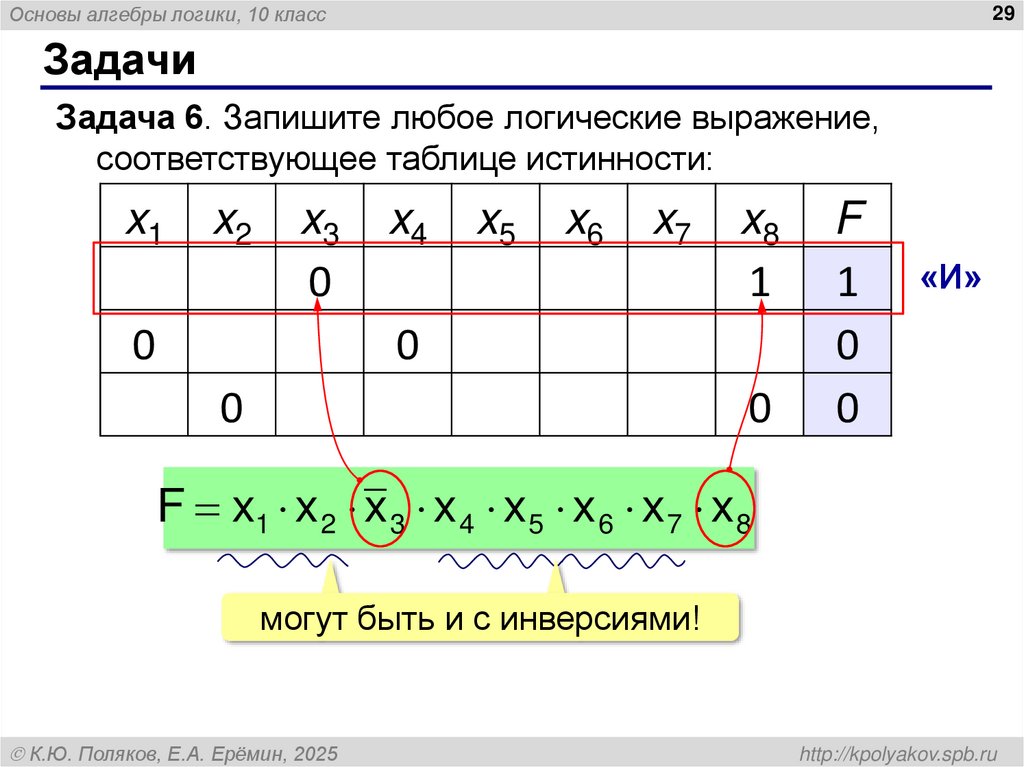
29. Задачи

Основы алгебры логики, 10 класс
29
Задачи
Задача 6. Запишите любое логические выражение,
соответствующее таблице истинности:
x1
x2
x3
0
0
x4
x5
x6
x7
x8
1
0
0
0
F
1
0
0
«И»
F x1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
могут быть и с инверсиями!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

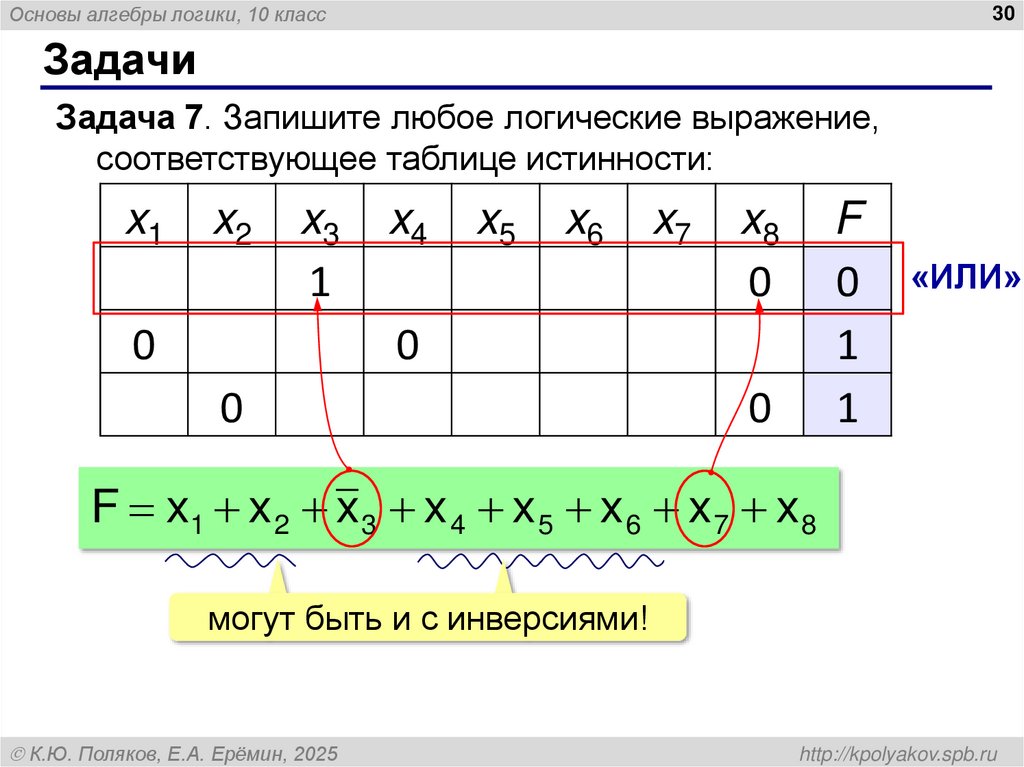
30. Задачи

Основы алгебры логики, 10 класс
30
Задачи
Задача 7. Запишите любое логические выражение,
соответствующее таблице истинности:
x1
x2
x3
1
0
x4
x5
x6
x7
x8
0
F
0
1
1
0
0
0
«ИЛИ»
F x1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
могут быть и с инверсиями!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

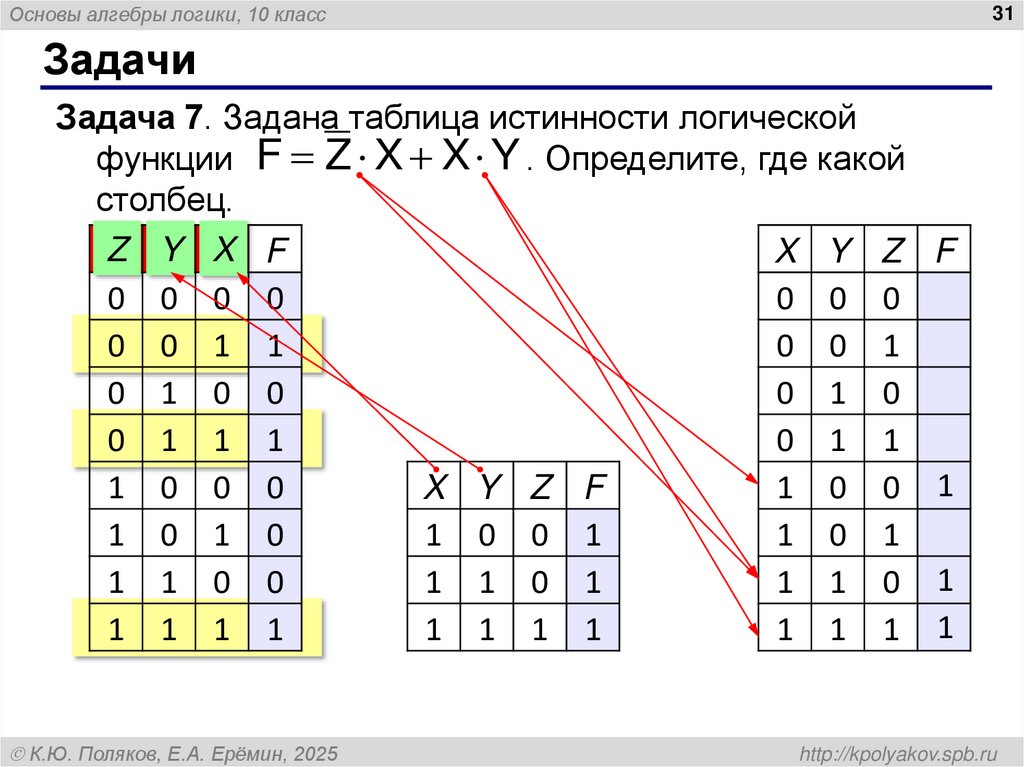
31. Задачи

Основы алгебры логики, 10 класс
31
Задачи
Задача 7. Задана таблица истинности логической
функции F Z X X Y . Определите, где какой
столбец.
Z Y
?
? X
? F
X Y Z
0 0 0 0
0 0 0
0 0 1 1
0 0 1
0 1 0 0
0 1 0
0 1 1 1
0 1 1
1 0 0 0
1 0 0
X Y Z F
1 0 1 0
1 0 0 1
1 0 1
1 1 0 0
1 1 0 1
1 1 0
1 1 1 1
1 1 1 1
1 1 1
К.Ю. Поляков, Е.А. Ерёмин, 2025
F
1
1
1
http://kpolyakov.spb.ru

32. Основы алгебры логики

32
Основы алгебры
логики
Упрощение
логических выражений
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

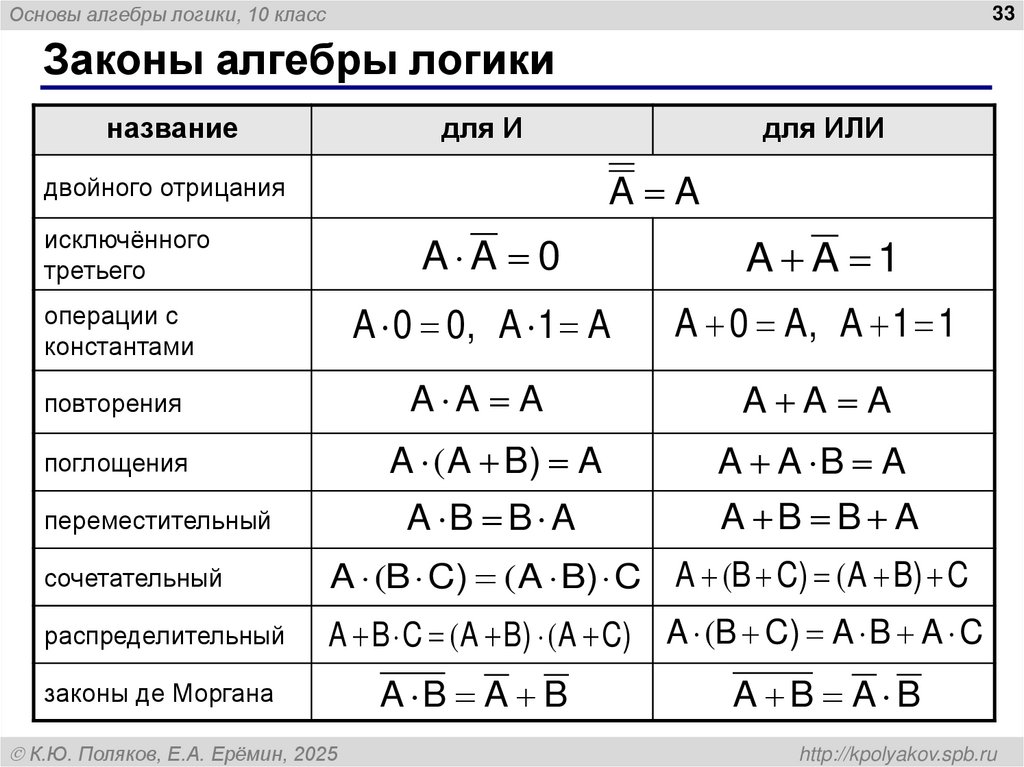
33. Законы алгебры логики

Основы алгебры логики, 10 класс
33
Законы алгебры логики
название
для И
для ИЛИ
A A
двойного отрицания
исключённого
третьего
A A 0
A A 1
операции с
константами
A 0 0, A 1 A
A 0 A, A 1 1
повторения
A A A
A A A
поглощения
A ( A B) A
A A B A
переместительный
A B B A
A B B A
сочетательный
A (B C) ( A B) C A (B C) ( A B) C
распределительный
A B C ( A B) ( A C)
A (B C) A B A C
законы де Моргана
A B A B
A B A B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

34. Упрощение логических выражений

Основы алгебры логики, 10 класс
34
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
A B A B A B
A B A B
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключённого третьего.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

35. Упрощение логических выражений

Основы алгебры логики, 10 класс
35
Упрощение логических выражений
Q M X H M X H (M M ) X H X H
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
раскрыли
распределительный
исключённого третьего
повторения
поглощения
? Как сделать проще?
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

36. Примеры:

Основы алгебры логики, 10 класс
36
Примеры:
F (A P ) ( Q A)
Ответ: F A P Q
F P (Q A P )
Ответ: F P Q A
F (A Q) P ((A Q ) ( Q A Q P))
Ответ: F A Q P
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

37. Задачи (упрощение)

Основы алгебры логики, 10 класс
37
Задачи (упрощение)
Какое логическое выражение равносильно выражению
A ¬(¬B C)?
1) A B C
1) ¬A ¬B ¬C
2) A B C
2) A ¬B ¬C
3) A B C
3) A B ¬C
4) A B C
4) A ¬B C
A ( B C) A B C A B C
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

38. Основы алгебры логики

38
Основы алгебры
логики
Логические уравнения
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

39. Логические уравнения

Основы алгебры логики, 10 класс
39
Логические уравнения
? Как решать?
((B C) A) ( A C D) 0
Способ 1. Построить таблицу истинности…
16 строк!
Способ 2. Свойство импликации:
(B C) A 1, A = 1 A C D 0
B C A 1 B = C = 0
D=0
Способ 3. Упрощение:
( B C A) ( A C D) 0
B C A ( A C D) 0
B C A A C D 0
B C A D 0
К.Ю. Поляков, Е.А. Ерёмин, 2025
A=1
B=C=D=0
http://kpolyakov.spb.ru

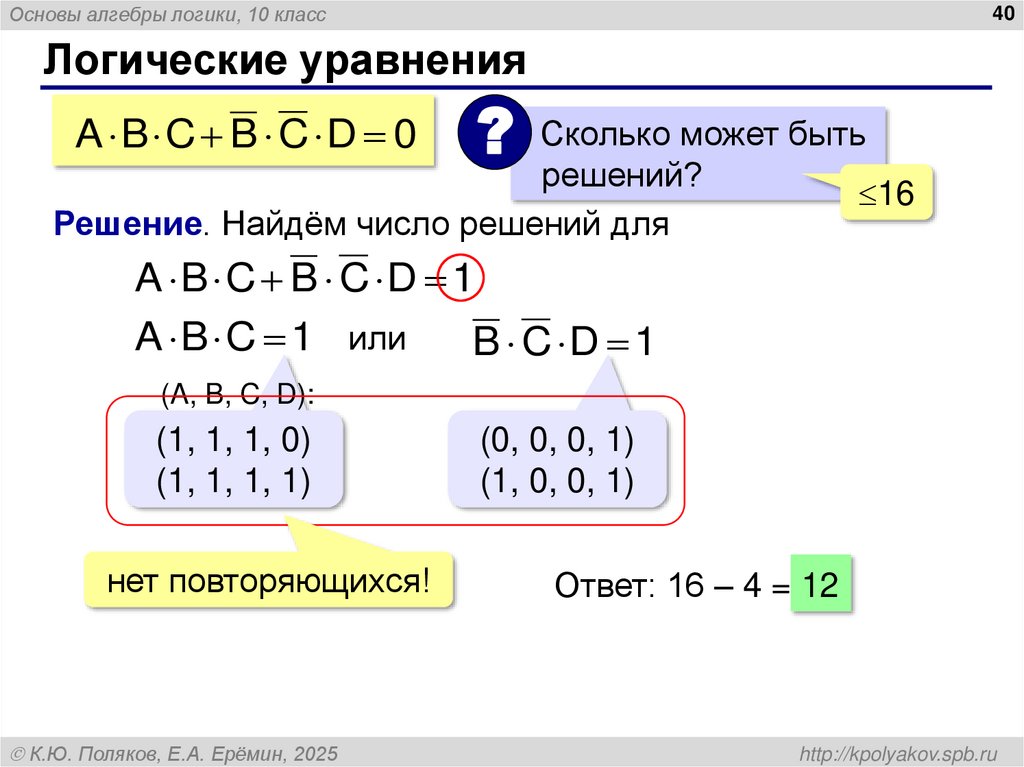
40. Логические уравнения

Основы алгебры логики, 10 класс
40
Логические уравнения
A B C B C D 0
? Сколько может быть
решений?
Решение. Найдём число решений для
16
A B C B C D 1
A B C 1 или
B C D 1
(A, B, C, D):
(1, 1, 1, 0)
(1, 1, 1, 1)
нет повторяющихся!
К.Ю. Поляков, Е.А. Ерёмин, 2025
(0, 0, 0, 1)
(1, 0, 0, 1)
Ответ: 16 – 4 = 12
http://kpolyakov.spb.ru

41. Логические уравнения

Основы алгебры логики, 10 класс
41
Логические уравнения
x1 x2 x3 x4 x5 0
00000
Запрещены 1!
x1 x2 x3 x4 x5 1
Ответ: 31
x1 x2 x3 x4 x5 1
Запрещены 0!
x1 x2 x3 x4 x5 0
? Сколько
решений?
11111
? Сколько
решений?
Ответ: 31
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

42. Логические уравнения

Основы алгебры логики, 10 класс
42
Логические уравнения
( x1 x2 ) ( x3 x4 ) 1
Запрещены 00** и **00!
x1 x2 x3 x4
пары битов:
3 3
0101 1001 1101
0110 1010 1110
0111 1011 1111
9 решений!
3
01, 10, 11
( x1 x2 ) ( x3 x4 ) 0
4 переменные – всего 24 = 16 вариантов
для уравнения с 1 в правой части – 9 решений
16 – 9 = 7 решений!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

43. Логические уравнения

Основы алгебры логики, 10 класс
43
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
? Сколько может быть
Решение:
решений?
64
Пусть x1 = 0, тогда…
x1 = x2 = x3 = x4 = x5 = x6 = 0
Пусть x1 = 1, тогда…
x1 = x2 = x3 = x4 = x5 = x6 = 1
Ответ: 2 решения,
000000 и 111111
( x1 ~ x2 ) ( x2 ~ x3 ) ( x3 ~ x4 ) ( x4 ~ x5 ) ( x5 ~ x6 ) 0
? Сколько решений?
К.Ю. Поляков, Е.А. Ерёмин, 2025
62
http://kpolyakov.spb.ru

44. Логические уравнения

Основы алгебры логики, 10 класс
44
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
Решение:
Пусть x1 = 0, тогда…
x1 = 0, x2 = 1, x3 = 0, x4 = 1, x5 = 0, x6 = 1
Пусть x1 = 1, тогда…
x1 = 1, x2 = 0, x3 = 1, x4 = 0, x5 = 1, x6 = 0
Ответ: 2 решения,
010101 и 101010
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 0
? Сколько решений?
К.Ю. Поляков, Е.А. Ерёмин, 2025
62
http://kpolyakov.spb.ru

45. Логические уравнения

Основы алгебры логики, 10 класс
45
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
? Когда нарушится?
Решение:
Рассмотрим цепочку x1 x2 x3 x4 x5 x6
1 0
! После 1 могут быть только 1!
Ответ: 000000
000001
000011
000111
001111
011111
111111
К.Ю. Поляков, Е.А. Ерёмин, 2025
7 решений
Для уравнения с N переменными:
N+1 решений.
http://kpolyakov.spb.ru

46. Системы логических уравнений

Основы алгебры логики, 10 класс
46
Системы логических уравнений
( x1 x2 ) ( x2 x3 ) ... ( x5 x6 ) 1
7 решений
( y1 y2 ) ( y2 y3 ) ... ( y4 y5 ) 1 6 решений
! Уравнения независимы!
всего 7 6 = 42 решения!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

47. Системы логических уравнений

Основы алгебры логики, 10 класс
47
Системы логических уравнений
( x1 x2 ) ( x2 x3 ) ... ( x5 x6 ) 1
7 решений
( y1 y2 ) ( y2 y3 ) ... ( y4 y5 ) 1 6 решений
y 2 x4 1
уравнение связи
y2 0 x4 {0, 1} X:
000000
y2 1 x4 1
000001
всего 7 4 + 4 2
= 36 решений!
К.Ю. Поляков, Е.А. Ерёмин, 2025
000011
000111
001111
011111
111111
Y:
00000 7
00001 7
00011 7
00111 7
01111 4
11111 4
http://kpolyakov.spb.ru

48. Системы логических уравнений

Основы алгебры логики, 10 класс
48
Системы логических уравнений
( x1 y1 ) ( x2 y2 )
( x2 y2 ) ( x3 y3 )
...
( x8 y8 ) ( x9 y9 )
Замена переменных:
z1 ( x1 y1 )
z2 ( x2 y2 )
…
z9 ( x9 x9 )
z1 z 2 , z 2 z3, z8 z9
z1 z 2 , z 2 z3, z8 z9
( z1 z2 ) ( z2 z3 ) ( z2 z3 ) ( z8 z9 ) 1
!
Биты чередуются!
К.Ю. Поляков, Е.А. Ерёмин, 2025
Решения: Z = 010101010,
Z = 101010101
http://kpolyakov.spb.ru

49. Системы логических уравнений

Основы алгебры логики, 10 класс
49
Системы логических уравнений
Решения: Z = 010101010,
Z = 101010101
zi ( xi yi )
9 битов
zi 0 ( xi , yi ) (0,1) (1,0)
zi 1 ( xi , yi ) (0,0) (1,1)
!
0 и 1 дают по
2 решения!
29 + 29 = 1024
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

50. Системы логических уравнений

Основы алгебры логики, 10 класс
50
Системы логических уравнений
( x1 y1 ) ( x2 y2 )
( x2 y2 ) ( x3 y3 )
...
( x5 y5 ) ( x6 y6 )
Замена переменных:
z1 ( x1 y1 )
z 2 ( x2 y 2 )
z6 ( x6 y6 )
( z1 z2 ) ( z2 z3 ) ( z5 z6 ) 1
«биты чередуются»
Решения: 010101, 101010
zi 1 ( xi , yi ) (1,1)
Ответ: 33+33= 54
zi 0 ( xi , yi ) (0,0)(0,1)(1,0)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

51. Основы алгебры логики

51
Основы алгебры
логики
Синтез логических выражений
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

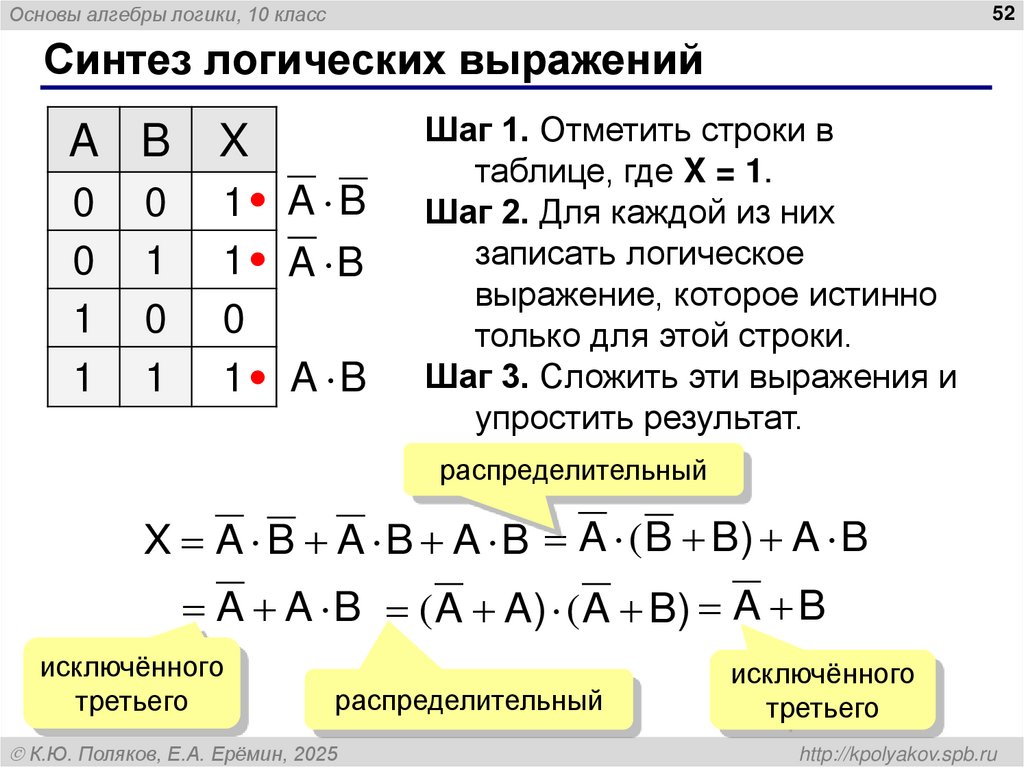
52. Синтез логических выражений

Основы алгебры логики, 10 класс
52
Синтез логических выражений
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 1.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат.
распределительный
X A B A B A B A (B B) A B
A A B ( A A) ( A B) A B
исключённого
третьего
распределительный
К.Ю. Поляков, Е.А. Ерёмин, 2025
исключённого
третьего
http://kpolyakov.spb.ru

53. Синтез логических выражений (2 способ)

Основы алгебры логики, 10 класс
53
Синтез логических выражений (2 способ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат, который
равен X .
Шаг 4. Сделать инверсию.
X A B X A B A B
? Когда удобнее применять 2-ой способ?
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

54. Синтез логических выражений (3 способ)

Основы алгебры логики, 10 класс
54
Синтез логических выражений (3 способ)
A B
X
0
0
1
1
0
1
0
1
0
1
0
1
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое ложно
только для этой строки.
Шаг 3. Перемножить эти
выражения и упростить
результат.
X (A B) ( A B) A A B A A B B B
B (A A) B B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

55. Синтез логических выражений

Основы алгебры логики, 10 класс
55
Синтез логических выражений
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2025
X A B C A B C
A B C
A B C
A B C
A B C
A B C
A B C
A B C A B C
A B C A B C
A B ( C C)
A B ( C C)
A C ( B B)
A B A B A C
A (B B) A C
A A C
(A A) ( A C) A C
http://kpolyakov.spb.ru

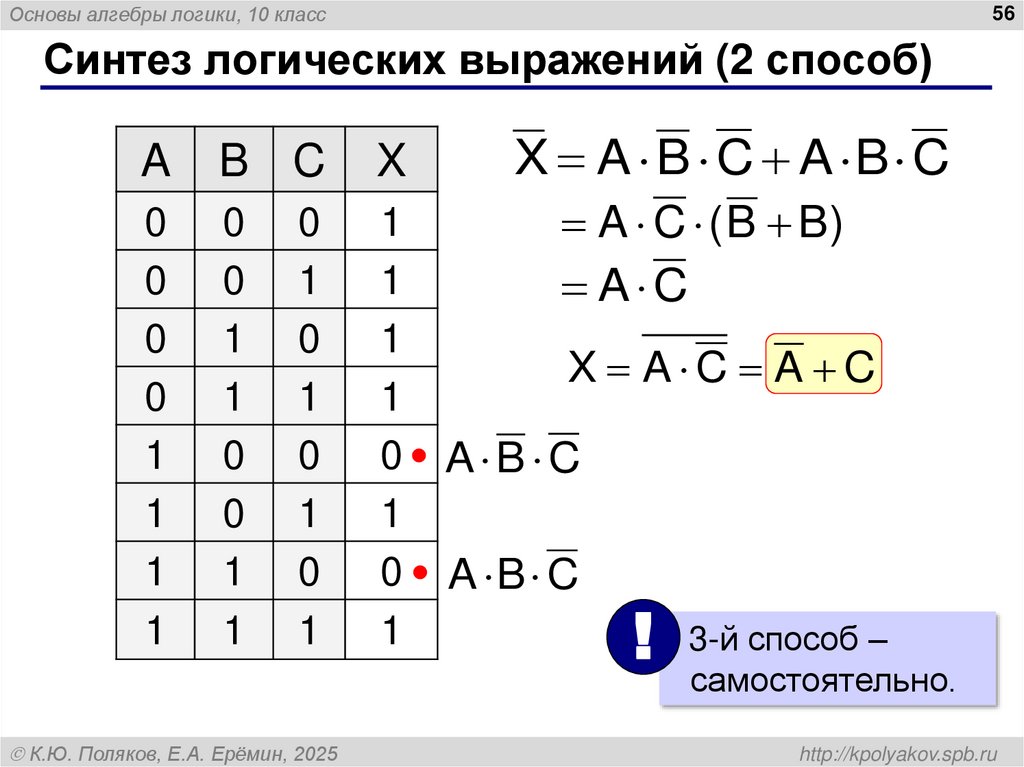
56. Синтез логических выражений (2 способ)

Основы алгебры логики, 10 класс
56
Синтез логических выражений (2 способ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
X A B C A B C
A C ( B B)
A C
X A C A C
A B C
A B C
! 3-й способ –
самостоятельно.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

57. Основы алгебры логики

57
Основы алгебры
логики
Множества и логика
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

58. Что такое множество?

Основы алгебры логики, 10 класс
58
Что такое множество?
Множество – некоторый набор элементов, каждый из
которых отличается от остальных.
пустое множество:
конечное число элементов: буквы русского алфавита
бесконечное число элементов: натуральные числа
Как задать множество?
• перечислением элементов
{Вася, Петя, Коля}
• логическим выражением:
{x: x > 0}
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

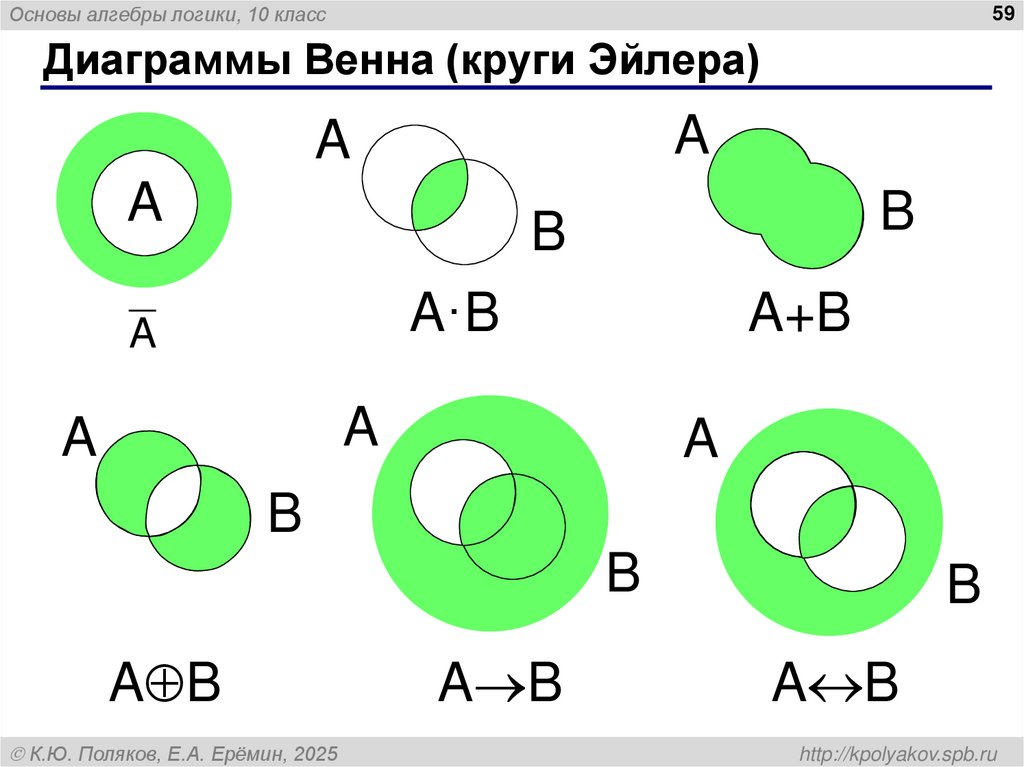
59. Диаграммы Венна (круги Эйлера)

Основы алгебры логики, 10 класс
59
Диаграммы Венна (круги Эйлера)
A
A
A
B
B
A·B
A
A+B
A
A
A
B
B
A B
К.Ю. Поляков, Е.А. Ерёмин, 2025
A B
B
A B
http://kpolyakov.spb.ru

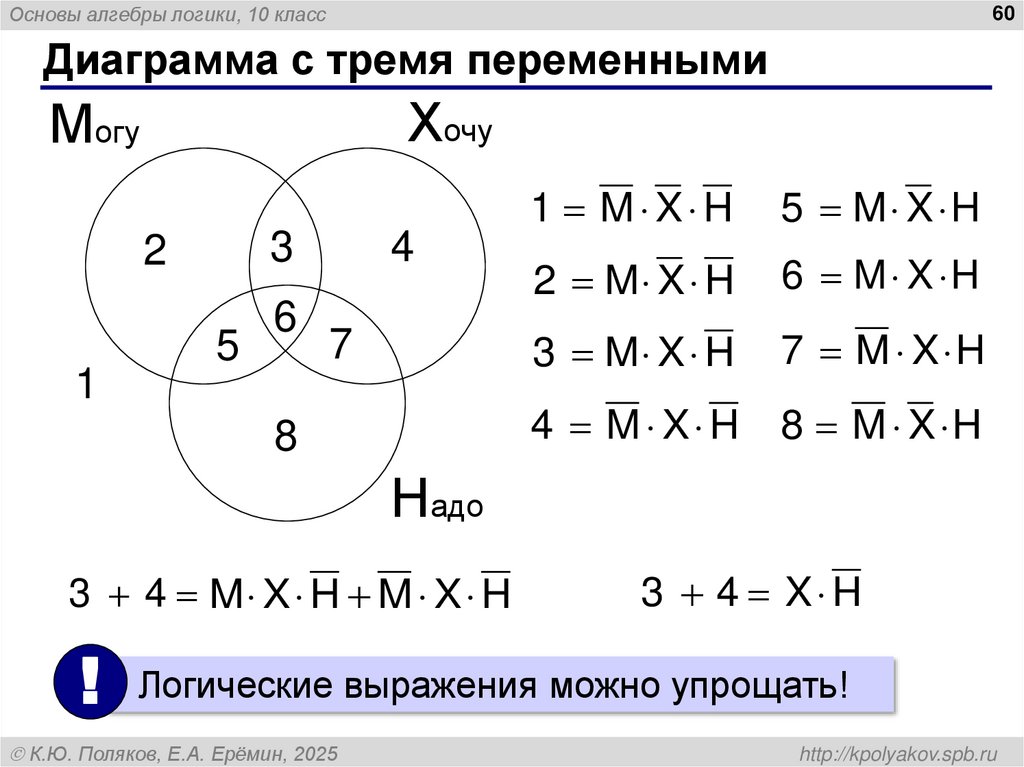
60. Диаграмма с тремя переменными

Основы алгебры логики, 10 класс
60
Диаграмма с тремя переменными
Хочу
Могу
3
2
1
5
6
4
7
8
1 M X H
5 M X H
2 M X H
6 M X H
3 M X H
7 M X H
4 M X H
8 M X H
Надо
3 4 M X H M X H
3 4 X H
! Логические выражения можно упрощать!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

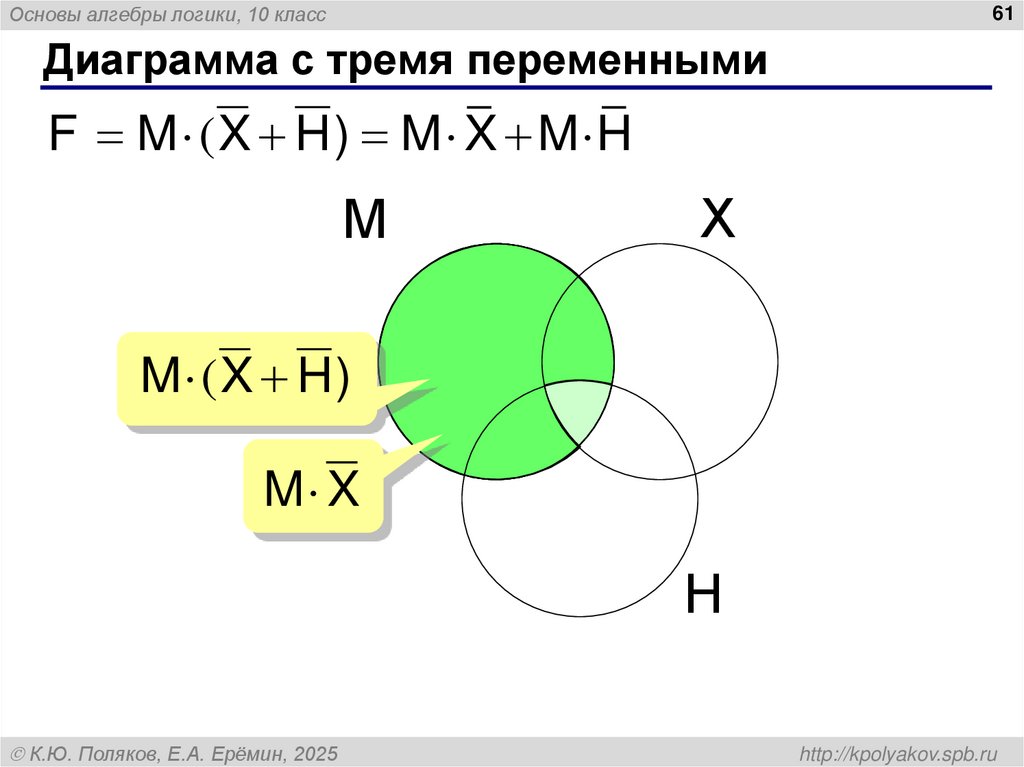
61. Диаграмма с тремя переменными

Основы алгебры логики, 10 класс
61
Диаграмма с тремя переменными
F M (X H ) M X M H
М
Х
M ( X H )
M X
Н
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

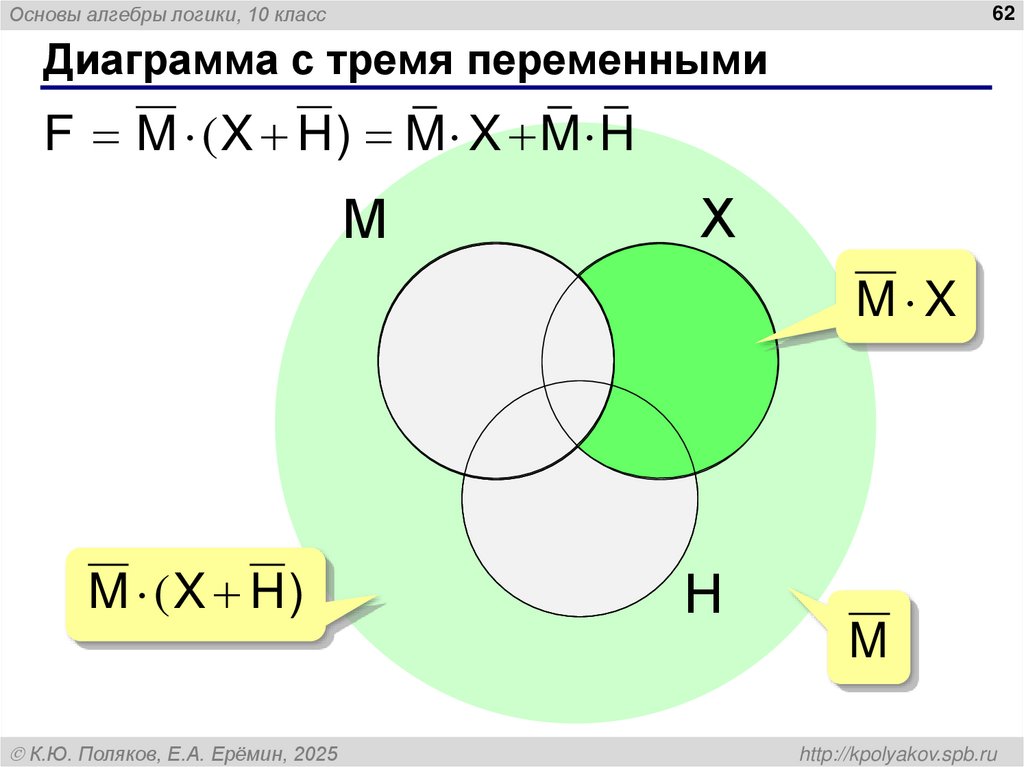
62. Диаграмма с тремя переменными

Основы алгебры логики, 10 класс
62
Диаграмма с тремя переменными
F M (X H) M X M H
М
Х
M X
M (X H)
К.Ю. Поляков, Е.А. Ерёмин, 2025
Н
M
http://kpolyakov.spb.ru

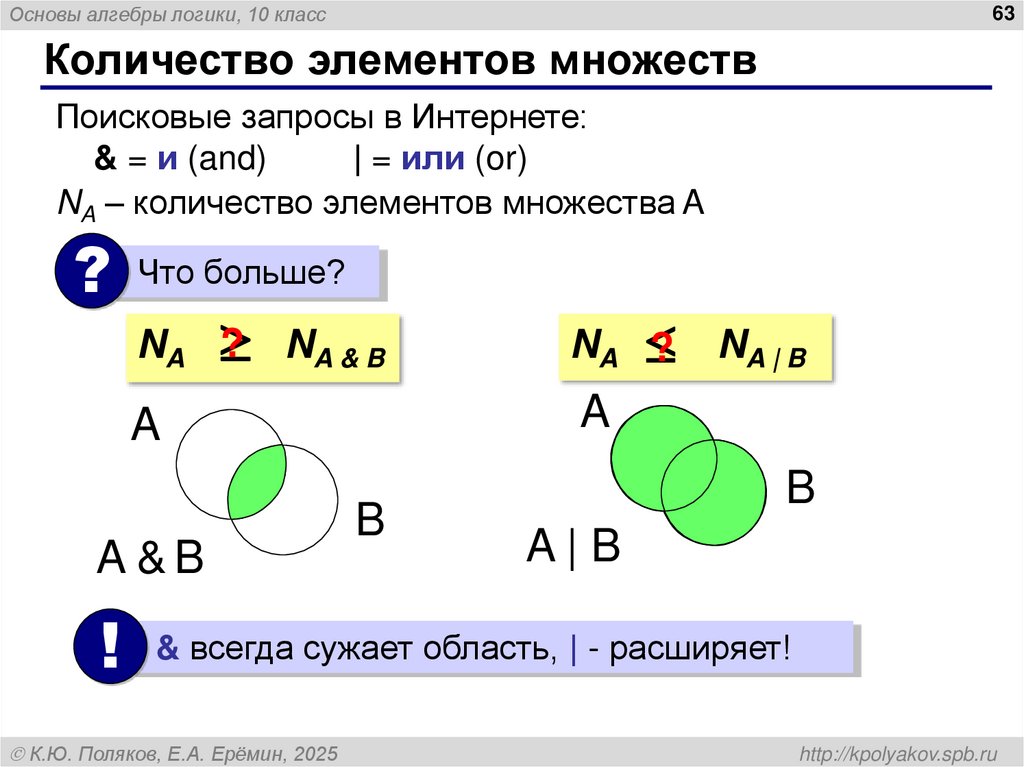
63. Количество элементов множеств

Основы алгебры логики, 10 класс
63
Количество элементов множеств
Поисковые запросы в Интернете:
& = и (and)
| = или (or)
NA – количество элементов множества A
? Что больше?
? NA & B
NA
NA
?
A
A
A &B
B
NA | B
B
A|B
! & всегда сужает область, | - расширяет!
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

64. Задачи

Основы алгебры логики, 10 класс
64
Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке возрастания
количества страниц, которые найдет поисковый сервер
по каждому запросу.
А: принтеры & сканеры & продажа
Б: принтеры | продажа
В: принтеры & продажа
Г: принтеры | сканеры | продажа
АВБГ
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

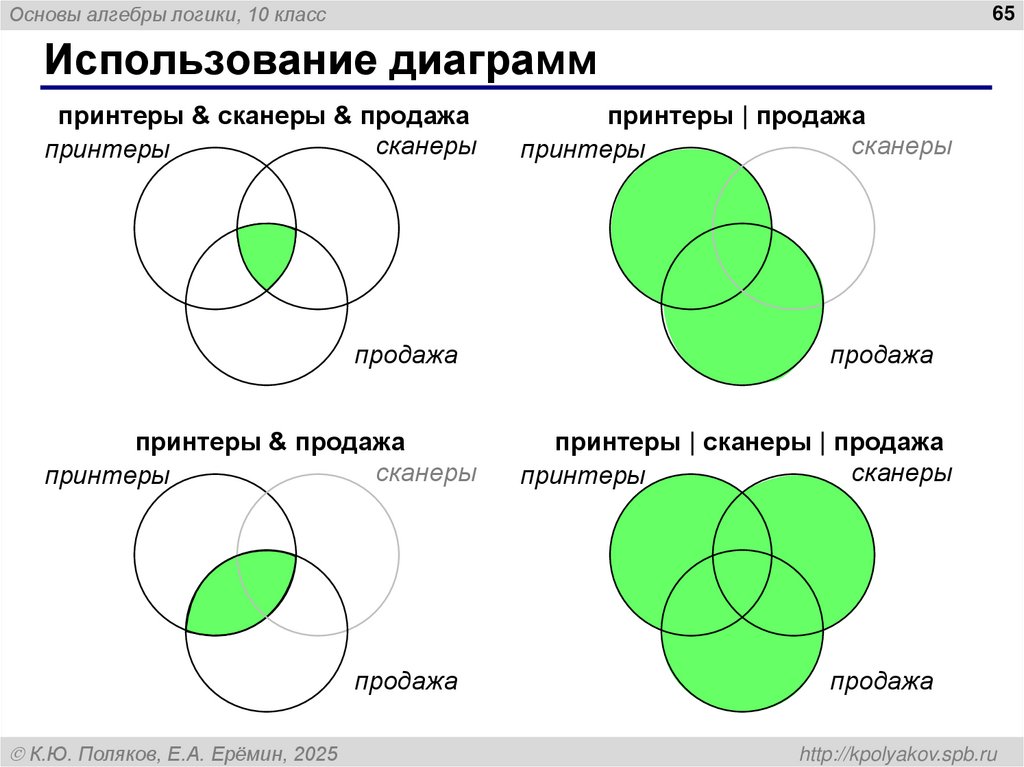
65. Использование диаграмм

Основы алгебры логики, 10 класс
65
Использование диаграмм
принтеры & сканеры & продажа
сканеры
принтеры
продажа
принтеры & продажа
сканеры
принтеры
продажа
К.Ю. Поляков, Е.А. Ерёмин, 2025
принтеры | продажа
сканеры
принтеры
продажа
принтеры | сканеры | продажа
сканеры
принтеры
продажа
http://kpolyakov.spb.ru

66. Задачи

Основы алгебры логики, 10 класс
66
Задачи
В таблице приведены запросы к поисковому серверу.
Расположите номера запросов в порядке убывания
количества страниц, которые найдет поисковый сервер
по каждому запросу.
А: принтеры & сканеры & продажа
Б: (принтеры & сканеры) | продажа
В: (принтеры | сканеры) & продажа
Г: принтеры | сканеры | продажа
ГБВА
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

67. Задачи

Основы алгебры логики, 10 класс
67
Задачи
Известно количество сайтов, которых находит поисковый
сервер по следующим запросам:
Запрос
огурцы
помидоры
огурцы & помидоры
Количество сайтов
100
200
50
Сколько сайтов будет найдено по запросу
огурцы | помидоры
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

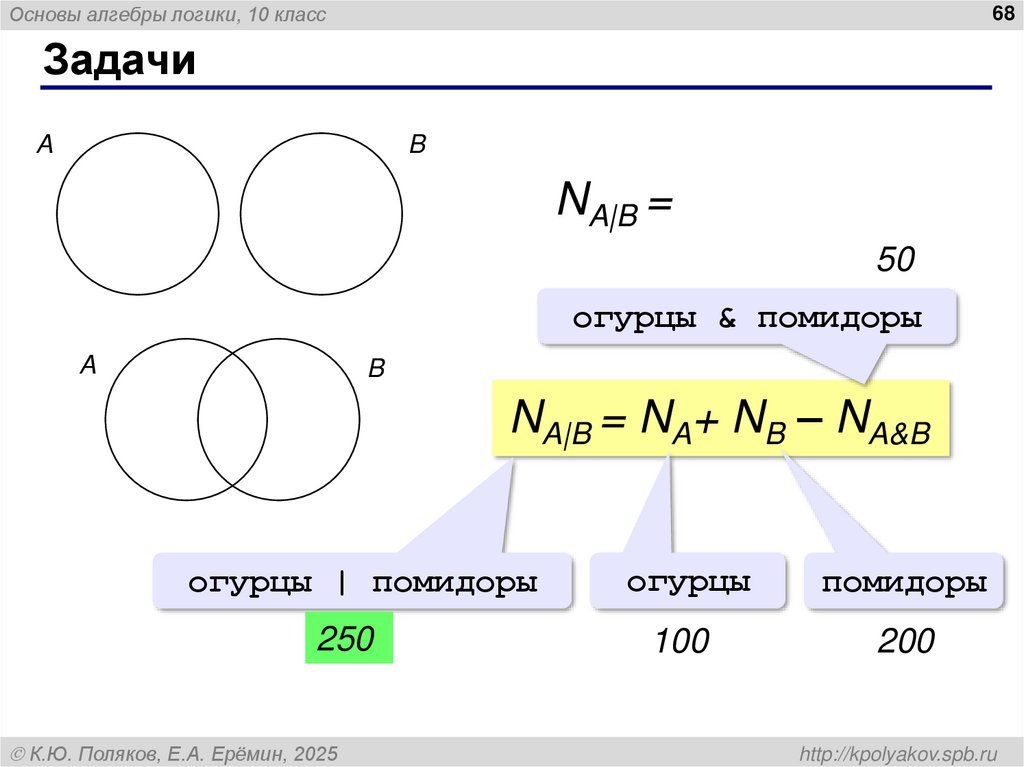
68. Задачи

Основы алгебры логики, 10 класс
68
Задачи
A
B
NA|B = NA+ NB
50
огурцы & помидоры
A
B
NA|B = NA+ NB – NA&B
огурцы | помидоры
огурцы
помидоры
250
100
200
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

69. Задачи

Основы алгебры логики, 10 класс
69
Задачи
Известно количество сайтов, которых находит поисковый
сервер по следующим запросам:
Запрос
Количество
сайтов
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак & Рубин
! Общее условие с & можно отбросить !
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

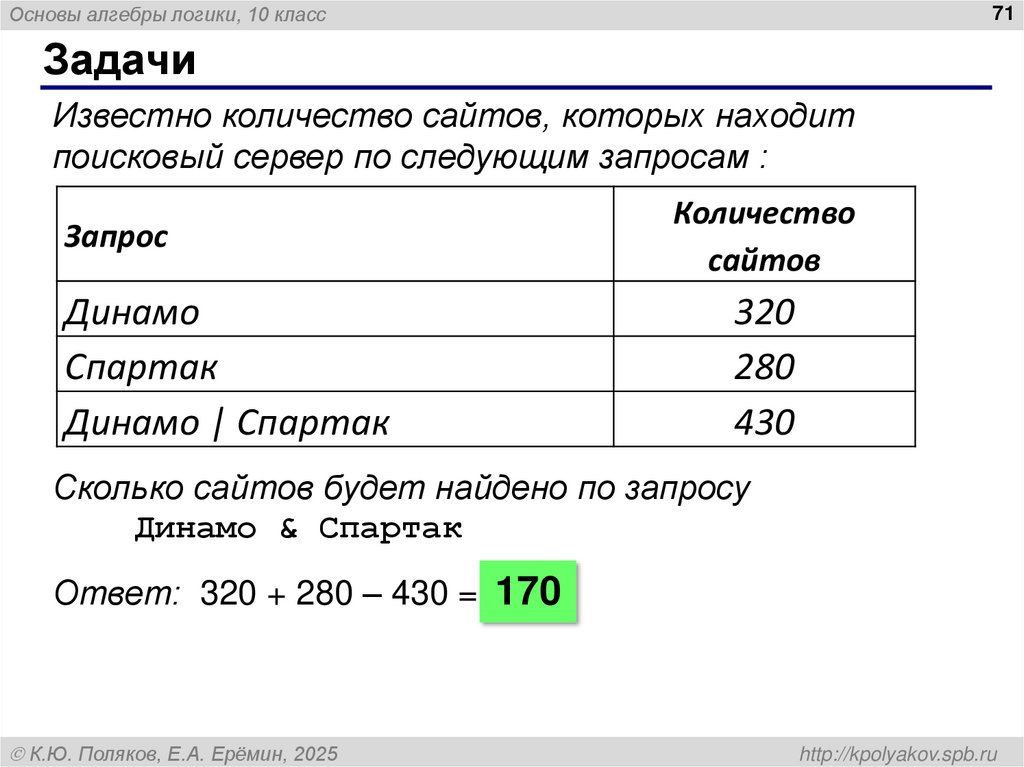
70. Задачи

Основы алгебры логики, 10 класс
71
Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
Динамо
Спартак
Динамо | Спартак
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак
Ответ: 320 + 280 – 430 = 170
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

71. Задачи

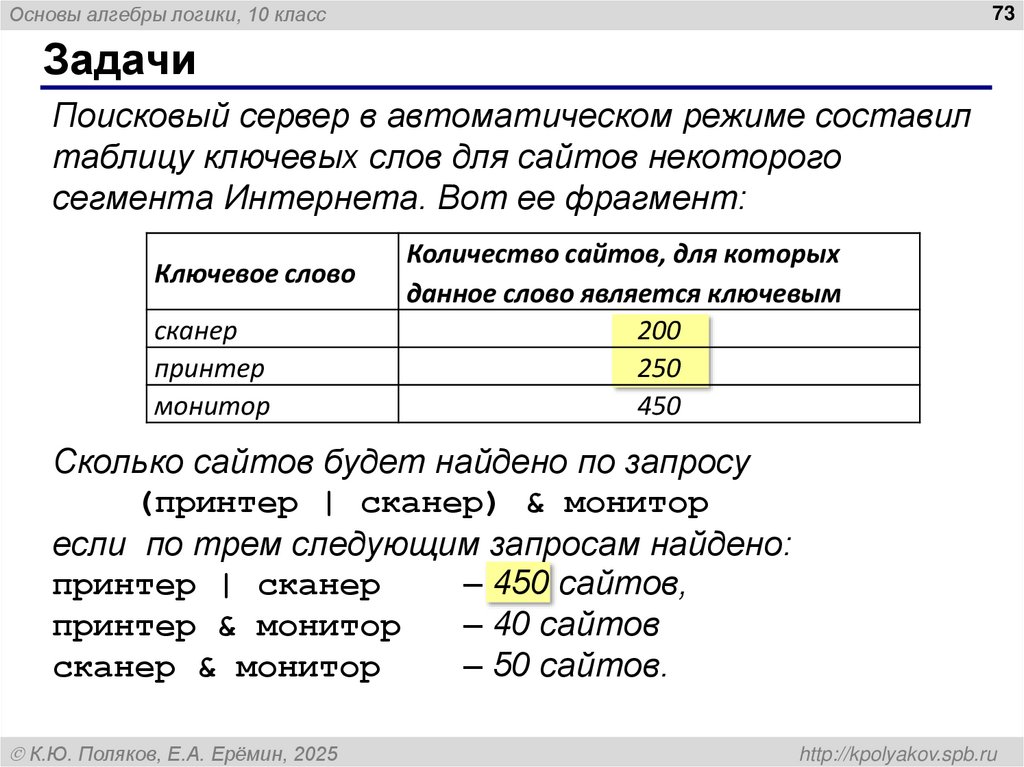
Основы алгебры логики, 10 класс
73
Задачи
Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов некоторого
сегмента Интернета. Вот ее фрагмент:
Ключевое слово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если по трем следующим запросам найдено:
принтер | сканер
– 450 сайтов,
принтер & монитор
– 40 сайтов
сканер & монитор
– 50 сайтов.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

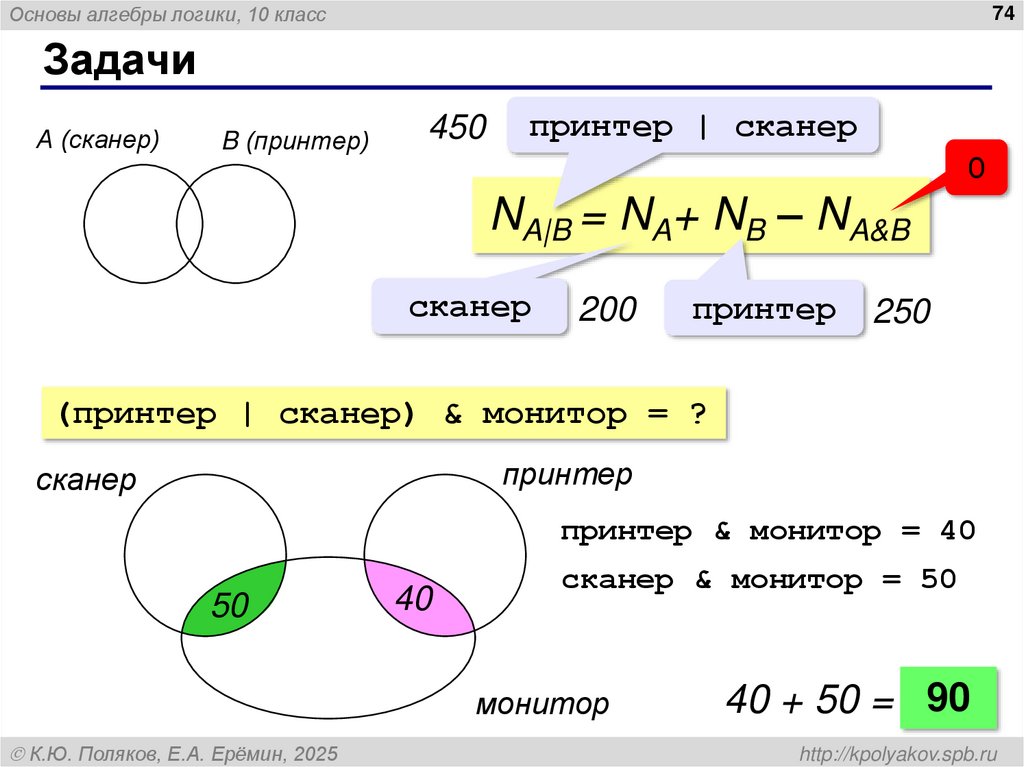
72. Задачи

Основы алгебры логики, 10 класс
74
Задачи
А (сканер)
B (принтер)
450
принтер | сканер
0
NA|B = NA+ NB – NA&B
сканер
200
принтер
250
(принтер | сканер) & монитор = ?
принтер
сканер
принтер & монитор = 40
50
40
сканер & монитор = 50
монитор
К.Ю. Поляков, Е.А. Ерёмин, 2025
40 + 50 = 90
http://kpolyakov.spb.ru

73. Задачи

Основы алгебры логики, 10 класс
75
Сложная задача
Ниже приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте
Интернета:
мезозой
500
кроманьонец
600
неандерталец
700
мезозой | кроманьонец
800
мезозой | неандерталец
1000
неандерталец & (мезозой | кроманьонец) 200
Сколько страниц будет найдено по запросу
кроманьонец & (мезозой | неандерталец)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

74. Задачи

Основы алгебры логики, 10 класс
76
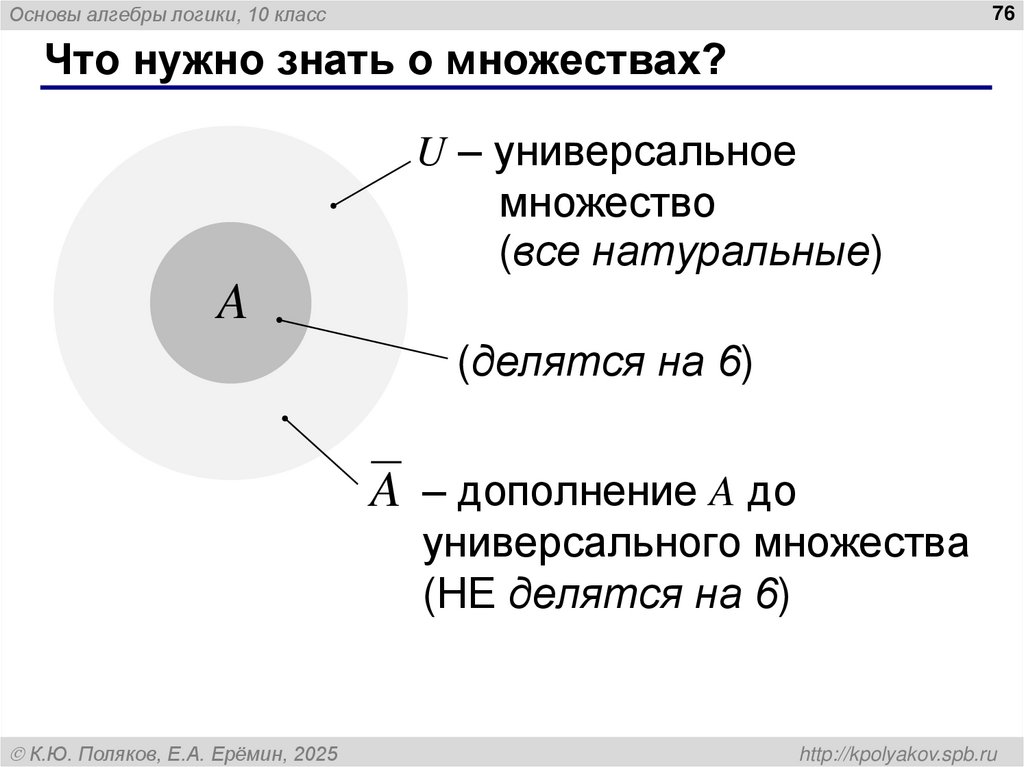
Что нужно знать о множествах?
U – универсальное
множество
(все натуральные)
A
(делятся на 6)
A – дополнение A до
универсального множества
(НЕ делятся на 6)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

75. Сложная задача

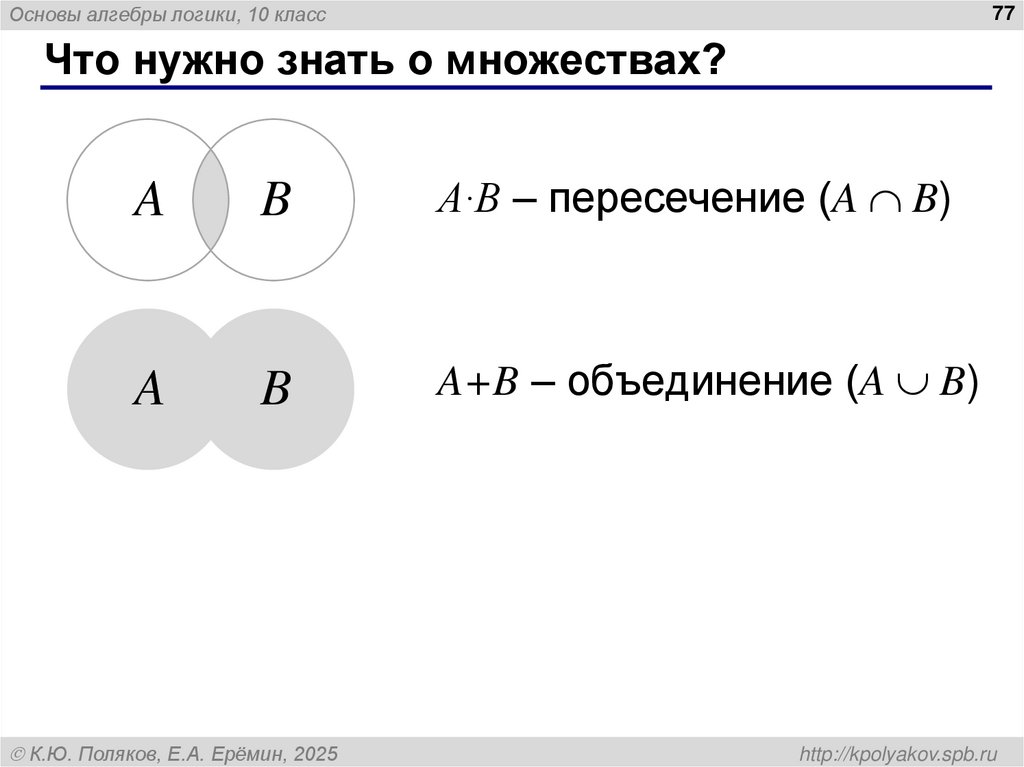
Основы алгебры логики, 10 класс
77
Что нужно знать о множествах?
A
B
A·B – пересечение (A B)
A
B
A+B – объединение (A B)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

76. Что нужно знать о множествах?

Основы алгебры логики, 10 класс
78
Множества и логические функции
Множество задаётся логической функцией
A
x A
A(x) = 1
A
A( x) 1 x A
x A
A
B
A( x) B( x) 1 x A·B
A
B
A( x) B( x) 1 x A+B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

77. Что нужно знать о множествах?

Основы алгебры логики, 10 класс
79
Задача дополнения (I)
Задача 1. Каким должно быть множество A для того,
чтобы множество A + B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
это решение!
B B U A B
B ( x) 1
это условие
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U Amin B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

78. Множества и логические функции

Основы алгебры логики, 10 класс
80
Задача дополнения (II)
Задача 2. Каким должно быть множество A для того,
чтобы множество A B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
B B U A B A B
B( x ) 1
это условие
это решение!
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U ( A ) min B
К.Ю. Поляков, Е.А. Ерёмин, 2025
A B
Amax B
http://kpolyakov.spb.ru

79. Задача дополнения (I)

Основы алгебры логики, 10 класс
81
Общий подход к решению
1. Свести задачу к одной из базовых задач
Задача 1. A B 1
B A 1
Задача 2. A B 1 B A 1
2. Использовать готовое решение:
Задача 1. Amin B
Задача 2. Amax B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

80. Задача дополнения (II)

Основы алгебры логики, 10 класс
82
Задачи с отрезками
На числовой прямой даны два отрезка:
P = [37; 60] и Q = [40; 77]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
P (Q A P )
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

81. Общий подход к решению

Основы алгебры логики, 10 класс
83
Задачи с отрезками
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = [37; 60], Q = [40; 77]
Amin = [40; 60]
К.Ю. Поляков, Е.А. Ерёмин, 2025
длина 20
http://kpolyakov.spb.ru

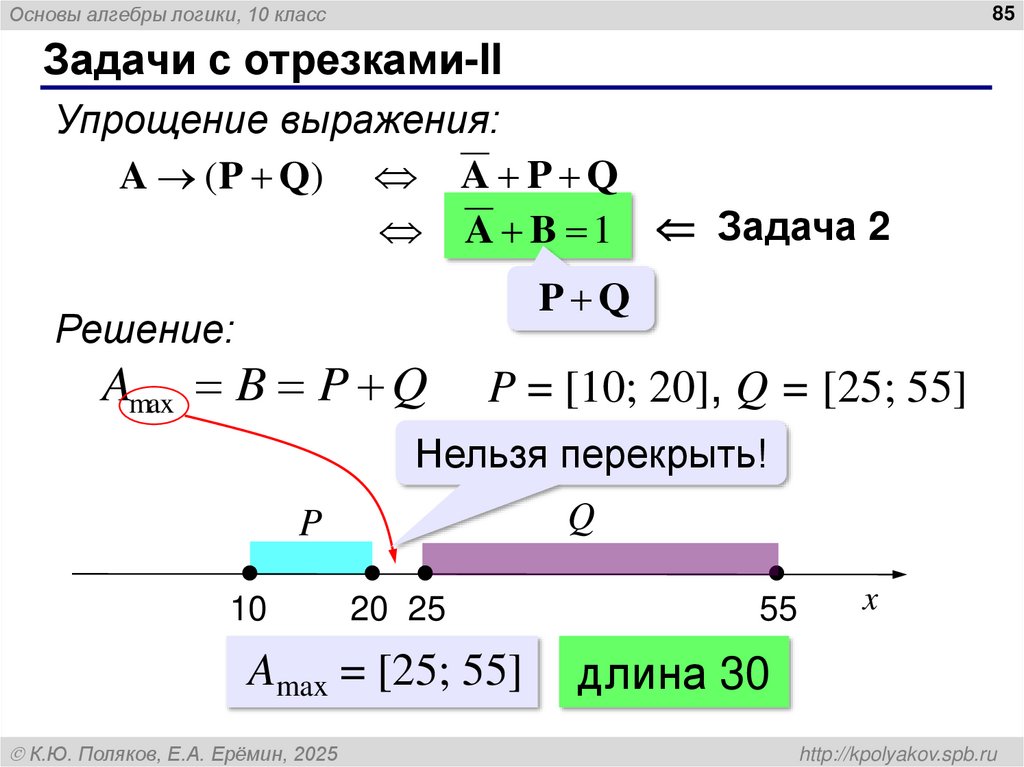
82. Задачи с отрезками

Основы алгебры логики, 10 класс
84
Задачи с отрезками-II
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наибольшую
возможную длину такого отрезка A, что
выражение
(x A) → ((x P) (x Q))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
A ( P Q)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

83. Задачи с отрезками

Основы алгебры логики, 10 класс
85
Задачи с отрезками-II
Упрощение выражения:
A ( P Q) A P Q
A B 1 Задача 2
P Q
Решение:
Amax B P Q
P = [10; 20], Q = [25; 55]
Нельзя перекрыть!
Q
P
10
20 25
Amax = [25; 55]
К.Ю. Поляков, Е.А. Ерёмин, 2025
55
x
длина 30
http://kpolyakov.spb.ru

84. Задачи с отрезками-II

Основы алгебры логики, 10 класс
86
Задачи с отрезками-III
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
((x P) (x Q)) → (x A)
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
(P Q) A
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

85. Задачи с отрезками-II

Основы алгебры логики, 10 класс
87
Задачи с отрезками-III
Упрощение выражения:
(P Q) A A P Q
A B 1
Задача 1
P Q
Решение:
Amin B P Q
P
10
P = [10; 20], Q = [25; 55]
Нужно перекрыть!
Q
20 25
Amin = [10; 55]
К.Ю. Поляков, Е.А. Ерёмин, 2025
55
x
длина 45
http://kpolyakov.spb.ru

86. Задачи с отрезками-III

Основы алгебры логики, 10 класс
88
Множества чисел
Элементами множеств А, P и Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
P (Q A P )
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

87. Задачи с отрезками-III

Основы алгебры логики, 10 класс
89
Множества чисел
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116}
Amin = {4, 8, 12}
К.Ю. Поляков, Е.А. Ерёмин, 2025
сумма 24
http://kpolyakov.spb.ru

88. Множества чисел

Основы алгебры логики, 10 класс
90
Множества чисел-II
Элементами множеств А, P и Q являются
натуральные числа, причём
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }.
Известно, что выражение
((x A) → ¬(x P)) (¬(x Q) → ¬(x A))
истинно при любом значении переменной х.
Определите наибольшее возможное количество
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
( A P ) ( Q A)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

89. Множества чисел

Основы алгебры логики, 10 класс
91
Множества чисел-II
Упрощение выражения:
(A P) (Q A) ( A P) (Q A)
A Q P Q A P A
A Q P Q A
A P Q
A B 1 Задача 2
Решение:
Amax B P Q
P Q
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }
Amax = { 3, 9, 15, 21, 24, 27, 30 }
К.Ю. Поляков, Е.А. Ерёмин, 2025
7 шт.
http://kpolyakov.spb.ru

90. Множества чисел-II

92
Основы алгебры
логики
Предикаты и кванторы
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

91. Множества чисел-II

Основы алгебры логики, 10 класс
93
Предикаты
Предикат (логическая функция) – это утверждение,
содержащее переменные.
Предикат-свойство – от одной переменной:
P(N) = «В городе N живут более 2 млн человек»
P(Москва) = 1
P(Якутск) = 0
Простое(x) = «x – простое число»
Спит(x) = «x всегда спит на уроке»
Предикат-отношение – от нескольких переменных:
Больше(x, y) = «x > y»
Живет(x, y) = «x живет в городе y»
Любит(x, y) = «x любит y»
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

92. Основы алгебры логики

Основы алгебры логики, 10 класс
94
Предикаты и кванторы
Предикаты задают множества:
P( x ) ( x 0)
P( x, y ) ( x y 1)
Предикаты, которые всегда истинны:
2
P( x) ( x 0) для всех вещественных чисел
«Для любого допустимого x утверждение P(x)
истинно»:
квантор
x P(x )
высказывание
Квантор – знак, обозначающий количество.
А (all – все) E (exists – существует)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

93. Предикаты

Основы алгебры логики, 10 класс
95
Кванторы
Какой квантор использовать?
моря соленые».
« …
кошки серые».
« …
числа чётные».
« …
« …
окуни – рыбы».
прямоугольники – квадраты».
« …
квадраты – прямоугольники».
« …
Истинно ли высказывание?
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x) ( x 2 0)
x P(x ) при P( x) ( x 2 0)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

94. Предикаты и кванторы

Основы алгебры логики, 10 класс
96
Кванторы
Дано:
A = «Все люди смертны» = 1.
B = «Сократ – человек» = 1.
Доказать:
C = «Сократ смертен» = 1.
Доказательство:
A
0
0
B
0
1
А B
1
1
1
1
0
1
0
1
P(x) = «x – человек»
Q(x) = «x – смертен»
x (P( x ) Q( x))
A = 1:
P( Сократ ) Q( Сократ) 1
при «x =Сократ»
P( Сократ ) 1
B = 1:
по свойствам импликации Q( Сократ ) 1
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

95. Кванторы

Основы алгебры логики, 10 класс
97
Несколько кванторов
Квантор связывает одну переменную:
x P( x, y ) – предикат от переменной y
y P( x, y ) – предикат от переменной x
Два квантора связывают две переменных:
x y P( x, y ) – высказывание «для любого x
существует y, при котором P(x,y)=1»
x y P( x, y ) – высказывание «существует x, такой
что при любом y верно P(x,y)=1»
Сравните два последних высказывания при:
P( x, y ) ( x y 0)
К.Ю. Поляков, Е.А. Ерёмин, 2025
P( x, y ) ( x y 0)
http://kpolyakov.spb.ru

96. Кванторы

Основы алгебры логики, 10 класс
98
Отрицание
НЕ «для любого x выполняется P(x)»
«существует x, при котором не выполняется P(x)»
x P(x) x P(x)
НЕ «существует x, при котором выполняется P(x)»
«для любого x не выполняется P(x)»
x P(x) x P(x)
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

97. Несколько кванторов

99
Основы алгебры
логики
Логические
элементы компьютера
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

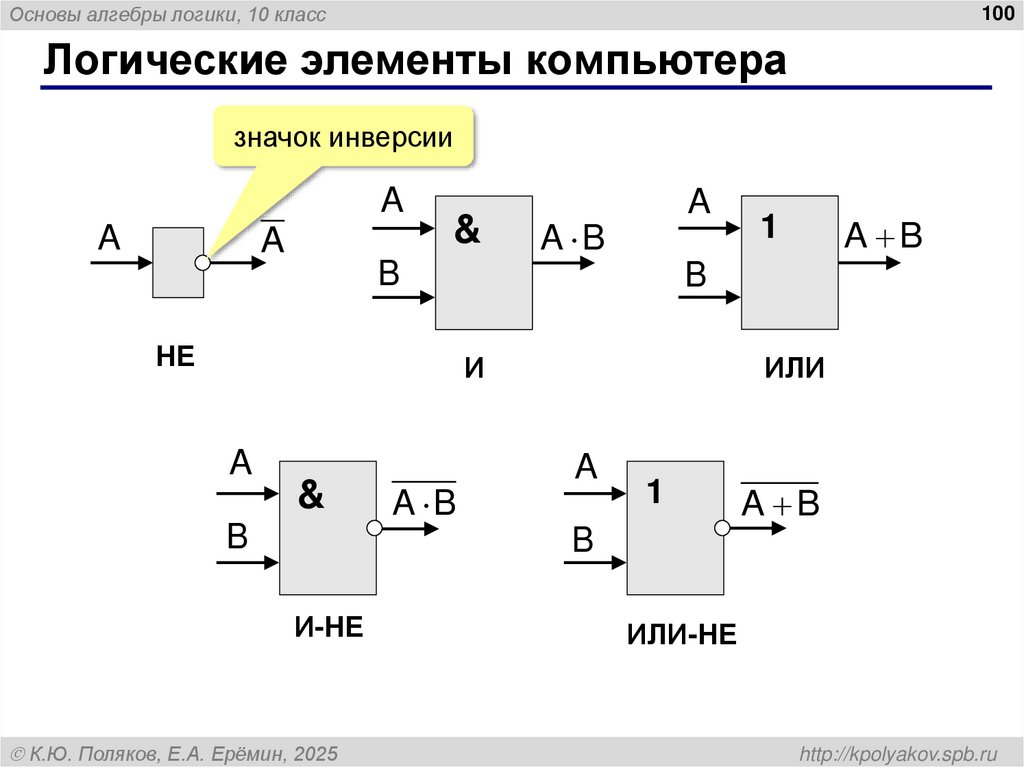
98. Отрицание

Основы алгебры логики, 10 класс
100
Логические элементы компьютера
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
A B
A B
1
ИЛИ
A
1
A B
B
И-НЕ
К.Ю. Поляков, Е.А. Ерёмин, 2025
ИЛИ-НЕ
http://kpolyakov.spb.ru

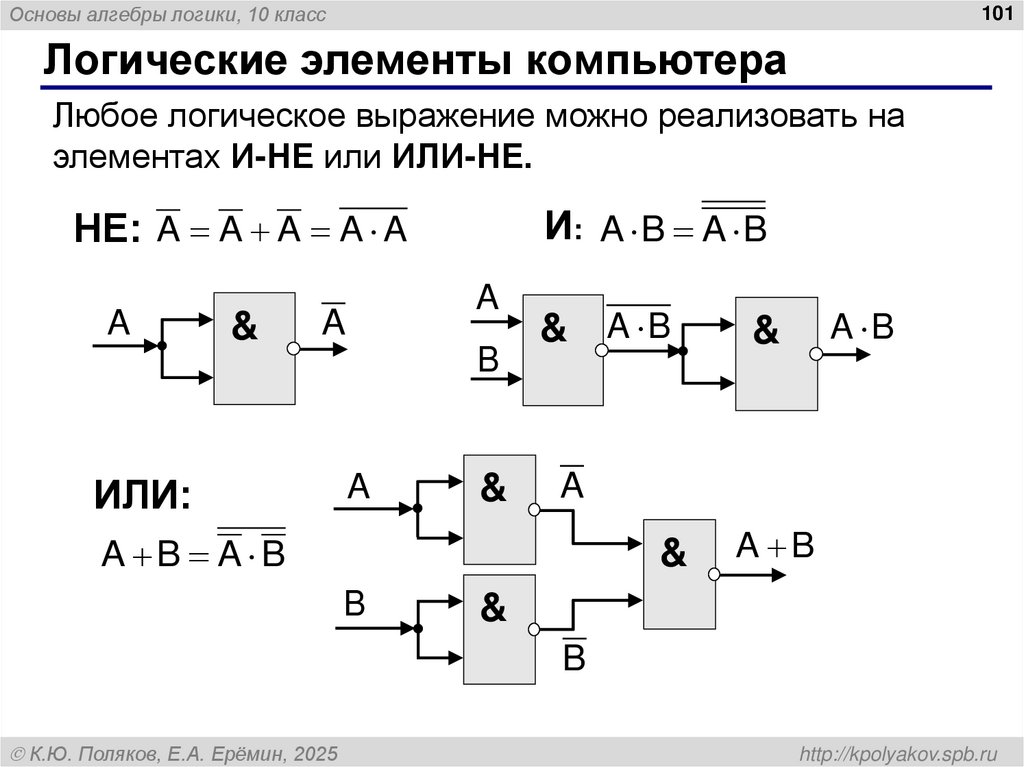
99. Основы алгебры логики

Основы алгебры логики, 10 класс
101
Логические элементы компьютера
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
A
A
ИЛИ:
B
A
&
& A B
A
A B A B
&
B
A B
&
A B
&
B
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

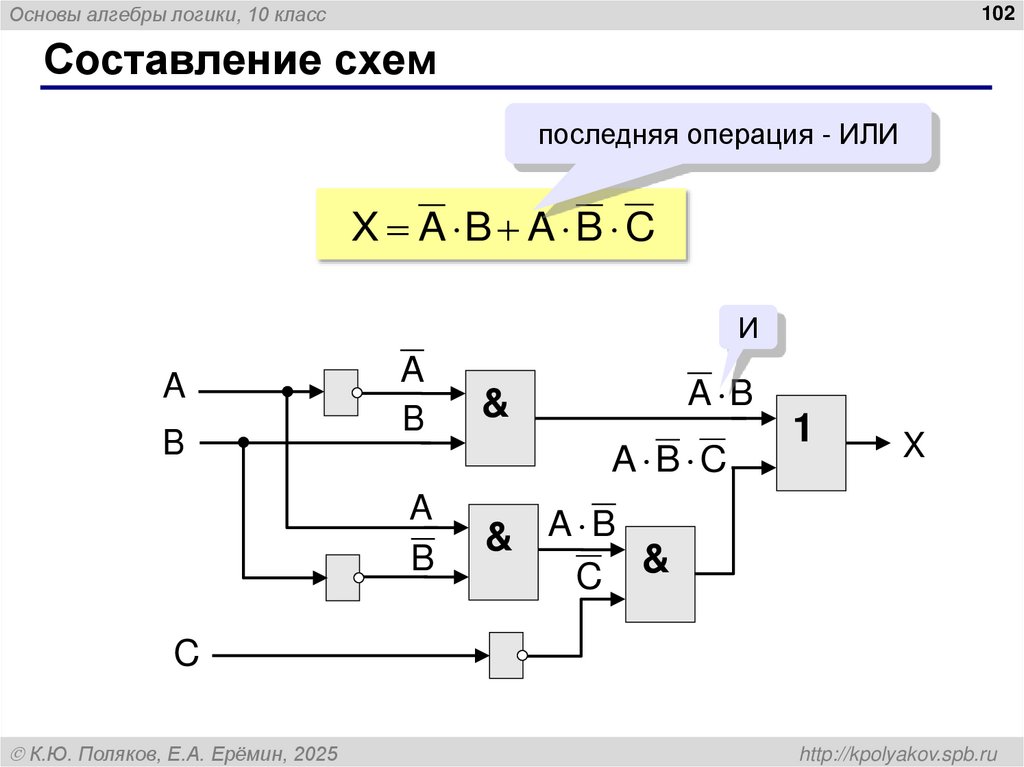
100. Логические элементы компьютера

Основы алгебры логики, 10 класс
102
Составление схем
последняя операция - ИЛИ
X A B A B C
И
A
B
A
B
&
A
B
& A B
A B
A B C
C
1
X
&
C
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

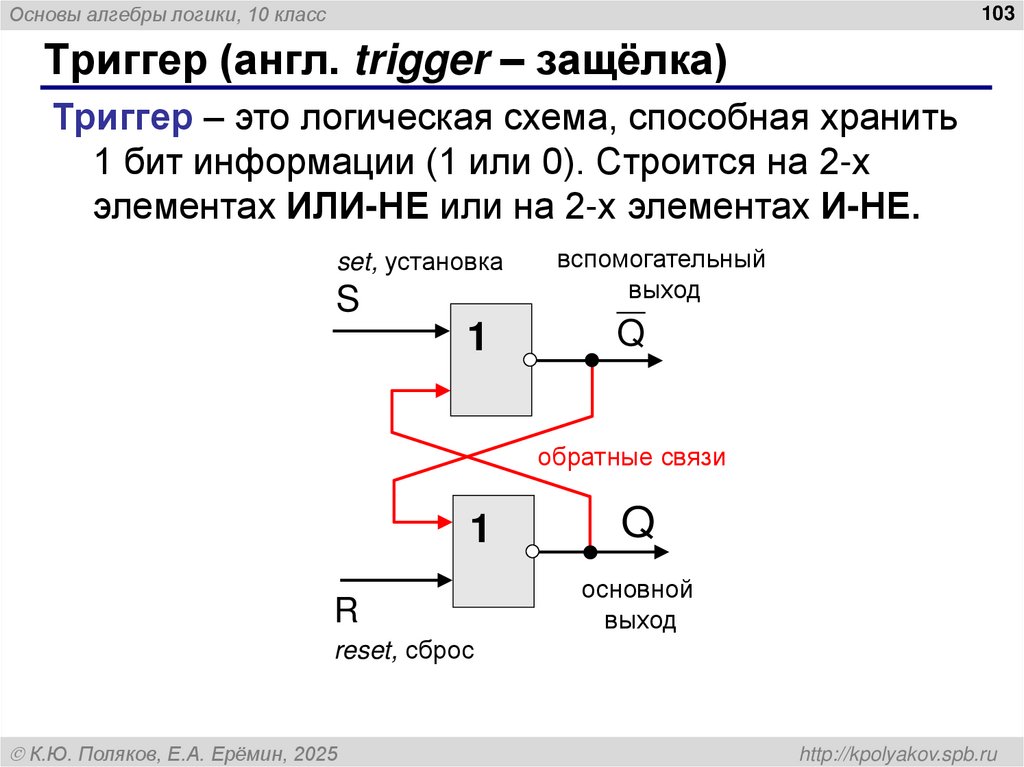
101. Логические элементы компьютера

Основы алгебры логики, 10 класс
103
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
1
вспомогательный
выход
Q
обратные связи
1
R
Q
основной
выход
reset, сброс
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

102. Составление схем

Основы алгебры логики, 10 класс
104
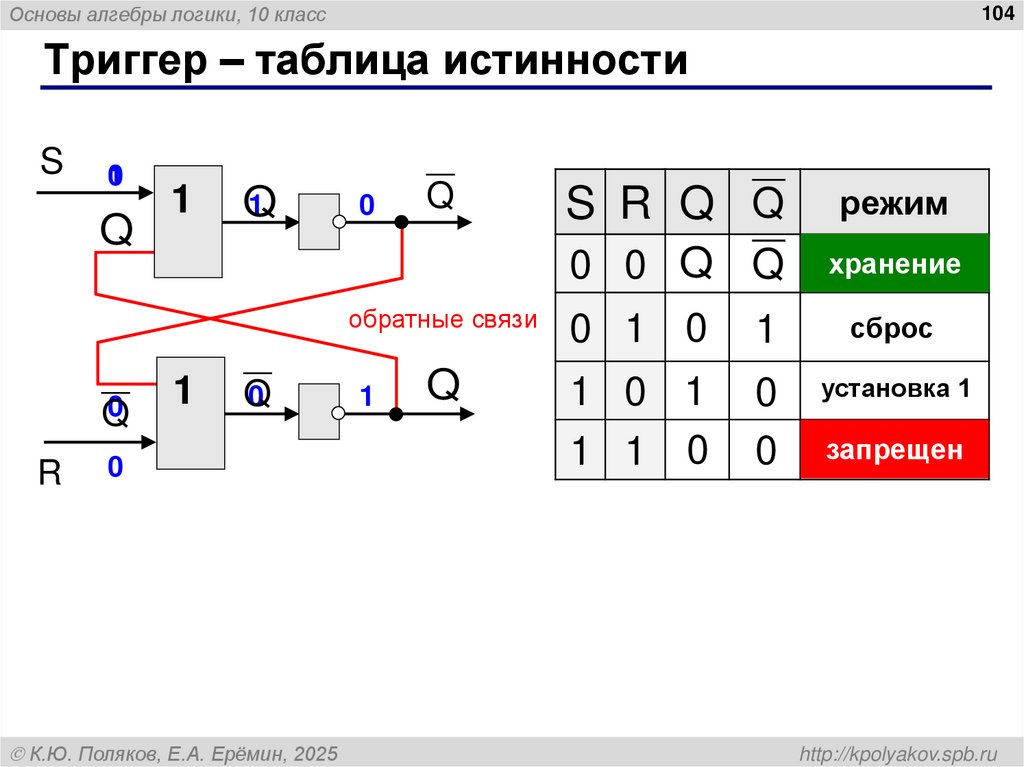
Триггер – таблица истинности
S
1
0
Q
0
Q
R
1
1
1
Q
0
Q
0
К.Ю. Поляков, Е.А. Ерёмин, 2025
0
Q
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1 0
1
сброс
Q
1 0 1
1 1 0
0
0
установка 1
1
запрещен
http://kpolyakov.spb.ru

103. Триггер (англ. trigger – защёлка)

Основы алгебры логики, 10 класс
105
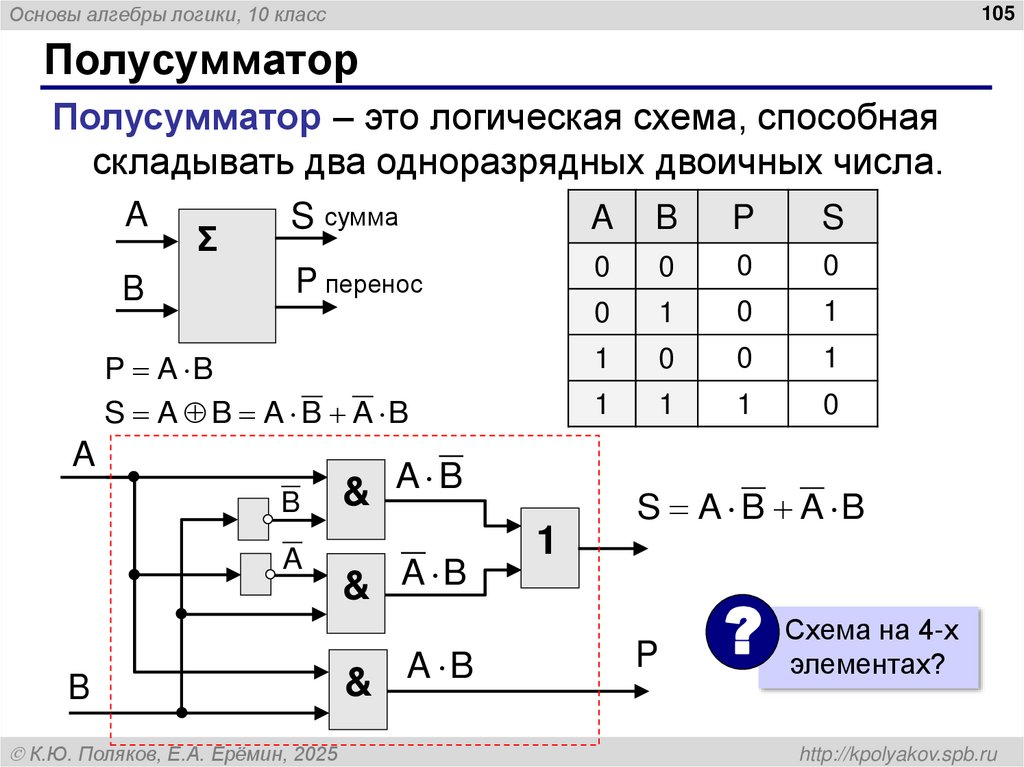
Полусумматор
Полусумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа.
A
S сумма
A B
P
S
Σ
B
P перенос
P A B
S A B A B A B
A
B
A
B
К.Ю. Поляков, Е.А. Ерёмин, 2025
& A B
& A B
& A B
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S A B A B
P
на 4-х
? Схема
элементах?
http://kpolyakov.spb.ru

104. Триггер – таблица истинности

Основы алгебры логики, 10 класс
106
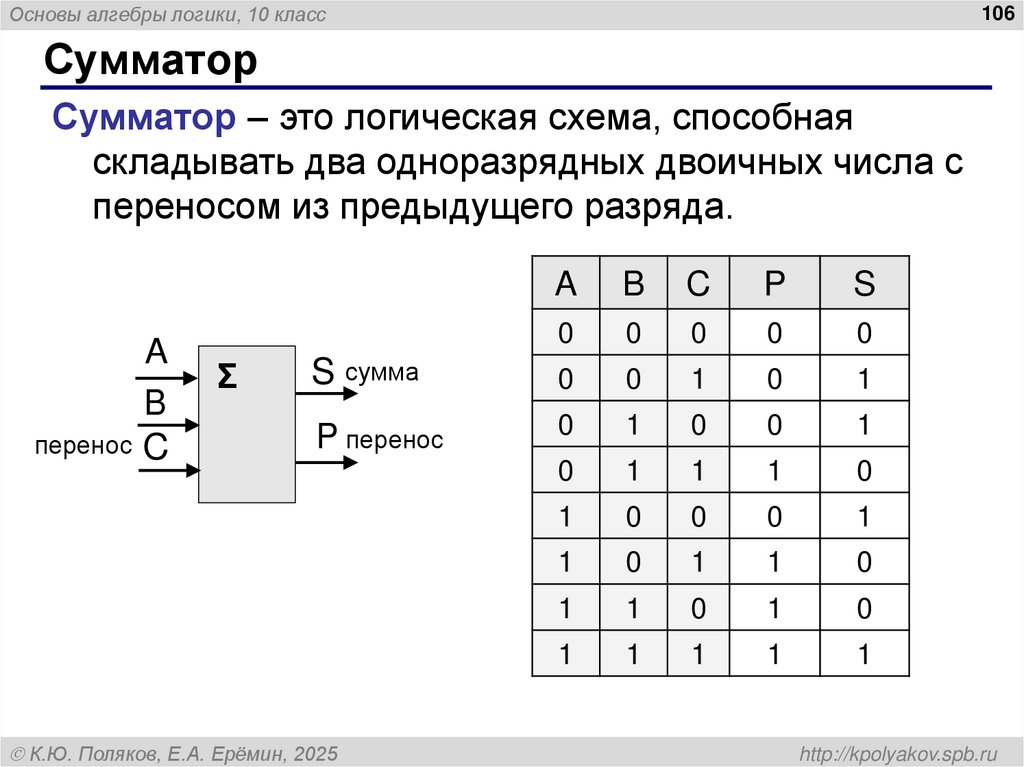
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа с
переносом из предыдущего разряда.
A
B
перенос C
Σ
A
B
C
P
S
0
0
0
0
0
S сумма
0
0
1
0
1
P перенос
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

105. Полусумматор

Основы алгебры логики, 10 класс
107
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
X
xn-1 xn-2 x0
110
Y
yn-1 yn-2 y0
011
Z p zn-1 zn-2 z0
1001
перенос
x0 0
y0 1
0
Σ
z0 1
x1 1
Σ
y1 1
p1 0
К.Ю. Поляков, Е.А. Ерёмин, 2025
z1 0
x2 1
Σ
y2 0
p2 1
z2 0
p 1
перенос
http://kpolyakov.spb.ru

106. Сумматор

Основы алгебры логики, 10 класс
108
Микросхемы
Микросхема (chip) — это электронная схема,
которая изготовлена так, что все её элементы
(транзисторы, резисторы, конденсаторы)
размещаются на одном кристалле
полупроводникового материала (Si, Ge, GaAs).
СБИС (сверхбольшая интегральная схема) – до
20 млрд элементов на кристалле.
Intel Core i9-10900K
10 млрд транзисторов
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

107. Многоразрядный сумматор

Основы алгебры логики, 10 класс
109
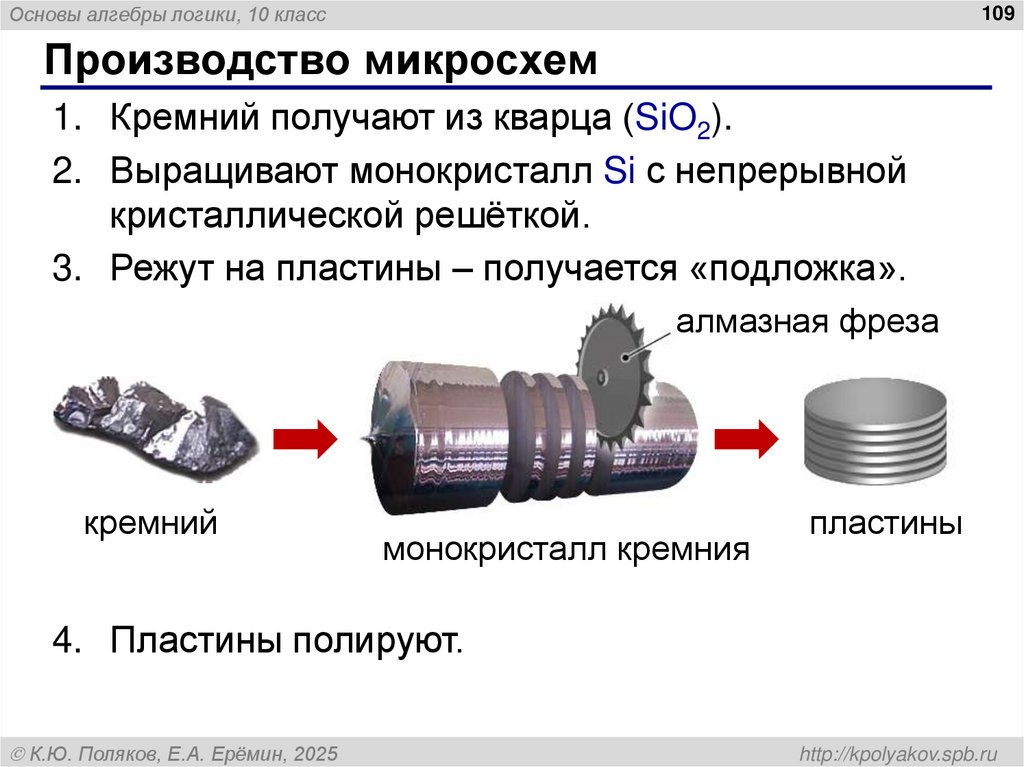
Производство микросхем
1. Кремний получают из кварца (SiO2).
2. Выращивают монокристалл Si с непрерывной
кристаллической решёткой.
3. Режут на пластины – получается «подложка».
алмазная фреза
кремний
монокристалл кремния
пластины
4. Пластины полируют.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

108. Микросхемы

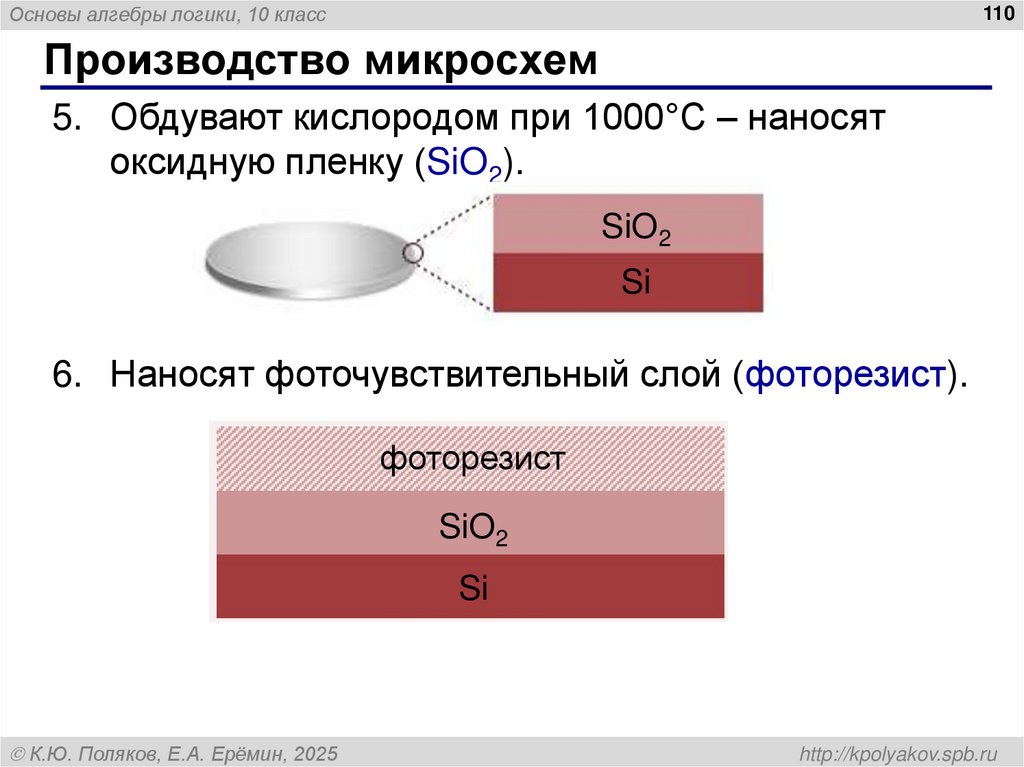
Основы алгебры логики, 10 класс
110
Производство микросхем
5. Обдувают кислородом при 1000°С – наносят
оксидную пленку (SiO2).
SiO2
Si
6. Наносят фоточувствительный слой (фоторезист).
фоторезист
SiO2
Si
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

109. Производство микросхем

Основы алгебры логики, 10 класс
111
Производство микросхем
7. Освещают через маску ультрафиолетовым
ультрафиолет
излучением
фоторезист
SiO2
Si
8. Проявителем удаляют слой фоторезиста там, где
его осветили ультрафиолетом.
фоторезист
SiO2
Si
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

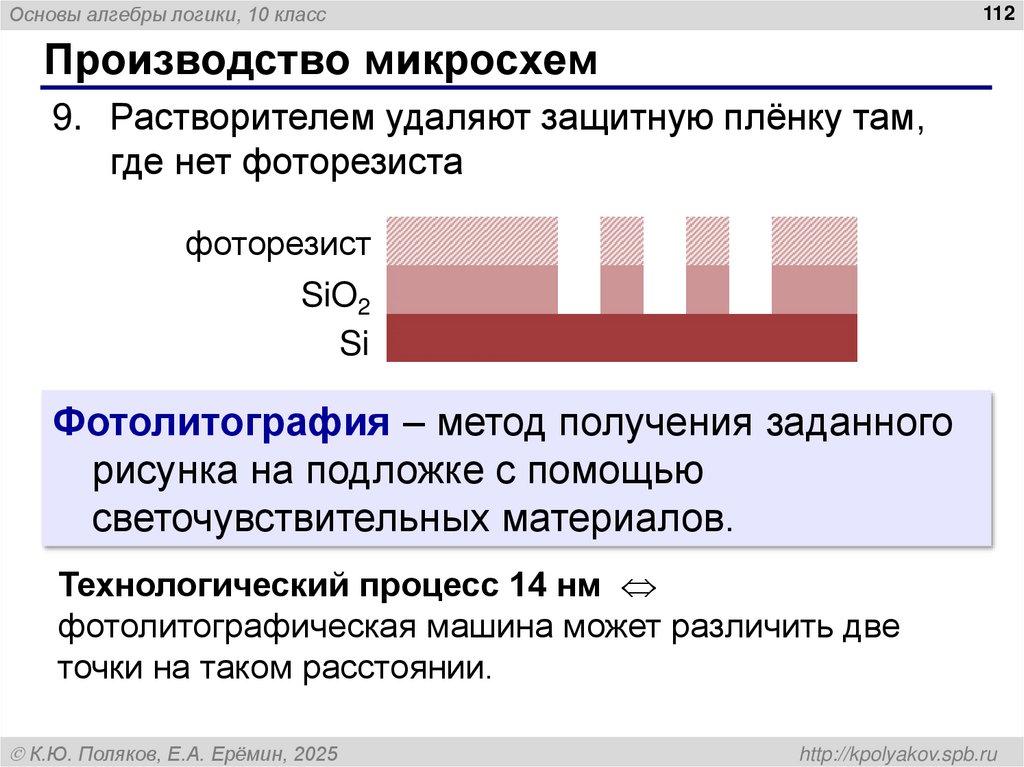
110. Производство микросхем

Основы алгебры логики, 10 класс
112
Производство микросхем
9. Растворителем удаляют защитную плёнку там,
где нет фоторезиста
фоторезист
SiO2
Si
Фотолитография – метод получения заданного
рисунка на подложке с помощью
светочувствительных материалов.
Технологический процесс 14 нм
фотолитографическая машина может различить две
точки на таком расстоянии.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

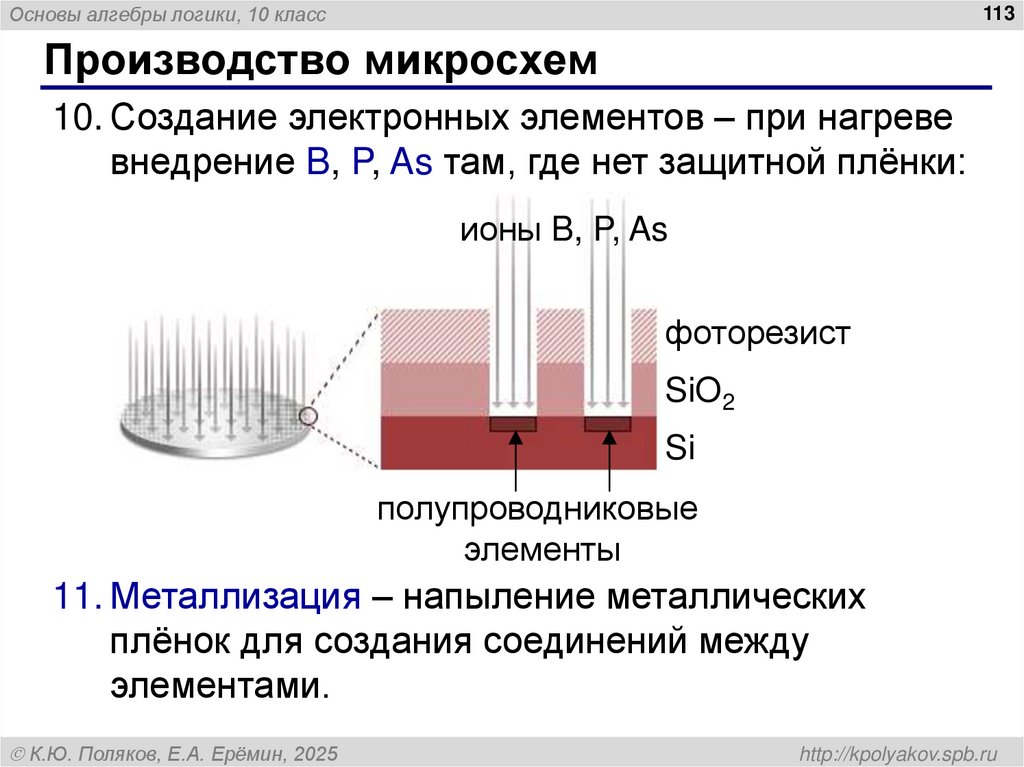
111. Производство микросхем

Основы алгебры логики, 10 класс
113
Производство микросхем
10. Создание электронных элементов – при нагреве
внедрение B, P, As там, где нет защитной плёнки:
ионы B, P, As
фоторезист
SiO2
Si
полупроводниковые
элементы
11. Металлизация – напыление металлических
плёнок для создания соединений между
элементами.
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

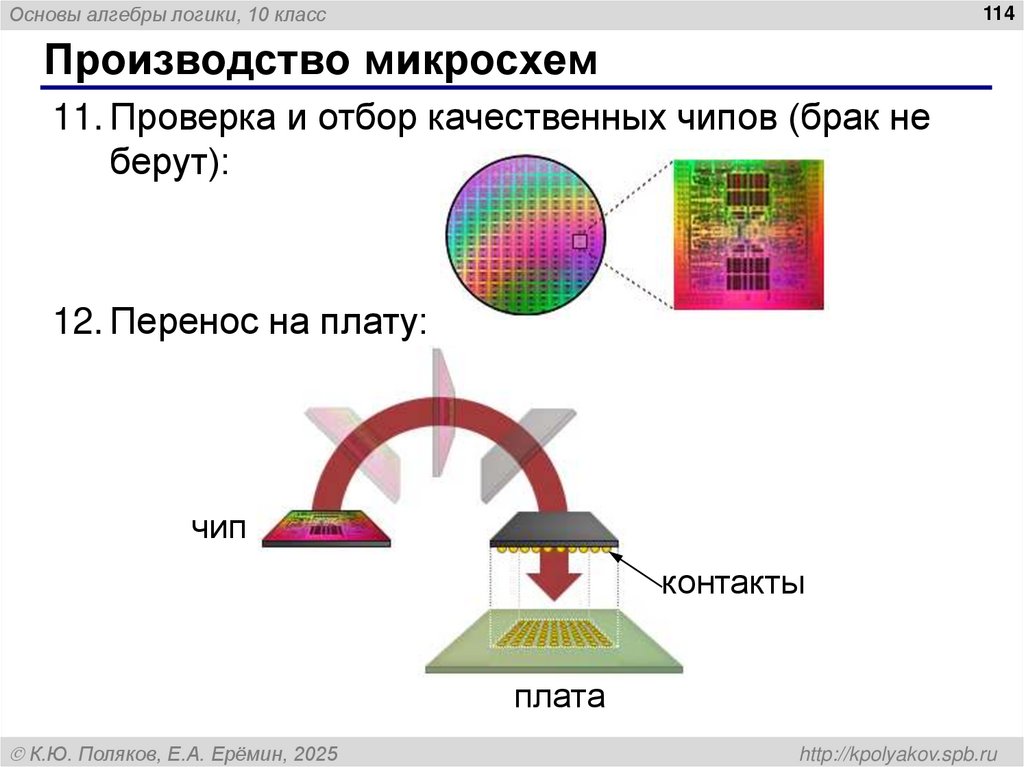
112. Производство микросхем

Основы алгебры логики, 10 класс
114
Производство микросхем
11. Проверка и отбор качественных чипов (брак не
берут):
12. Перенос на плату:
чип
контакты
плата
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

113. Производство микросхем

Основы алгебры логики, 10 класс
115
Производство микросхем
13. Установка радиатора для отвода тепла:
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

114. Производство микросхем

Основы алгебры логики, 10 класс
116
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 174, г. Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru

115. Производство микросхем

Основы алгебры логики, 10 класс
117
Источники иллюстраций
1.
2.
3.
4.
http://www.peoples.ru
http://ru.wikipedia.org
https://www.fujitsu.com
авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2025
http://kpolyakov.spb.ru