Similar presentations:
Логические основы компьютеров (§ 16 - § 23 ) - 2018
1. Логические основы компьютеров
1Логические основы
компьютеров
§ 16. Логические операции
§ 17. Логические выражения
§ 18. Упрощение логических выражений
§ 19. Логические уравнения
§ 20. Синтез логических выражений
§ 21. Множества и логика
§ 22. Предикаты и кванторы
§ 23. Логические элементы компьютера
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
2. Логические основы компьютеров
2Логические
основы
компьютеров
§ 16. Логика и компьютер
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
3. Вспомним известное…
Логические основы компьютеров, 10 класс3
Вспомним известное…
Логическое высказывание – это
повествовательное предложение, относительно
которого можно однозначно сказать, истинно оно
(0) или ложно (1).
Алгебра логики (булева алгебра) — это
математический аппарат, с помощью которого
записывают, вычисляют, упрощают и
преобразуют логические высказывания.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
4. Вспомним известное…
Логические основы компьютеров, 10 класс4
Вспомним известное…
Логическое выражение — это символическая
запись высказывания, которая может
содержать логические переменные и знаки
логических операций.
Логическая функция — это правило
преобразования входных логических значений
в выходные. Логическая функция задаётся
таблицей истинности.
Выражения:
A
A+A B
A (A+B)
К.Ю. Поляков, Е.А. Ерёмин, 2018
A
0
0
1
1
B
0
1
0
1
F
0
0
1
1
функция
http://kpolyakov.spb.ru
5. Операция НЕ (инверсия)
Логические основы компьютеров, 10 класс5
Операция НЕ (инверсия)
Если высказывание A истинно, то «не А» ложно, и
наоборот.
также A , A ,
А
не А
0
1
1
0
not A (Паскаль),
! A (Си)
таблица
истинности
операции НЕ
Таблица истинности логического выражения Х – это
таблица, где в левой части записываются все
возможные комбинации значений исходных данных,
а в правой – значение выражения Х для каждой
комбинации.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
6. Операция И
Логические основы компьютеров, 10 класс6
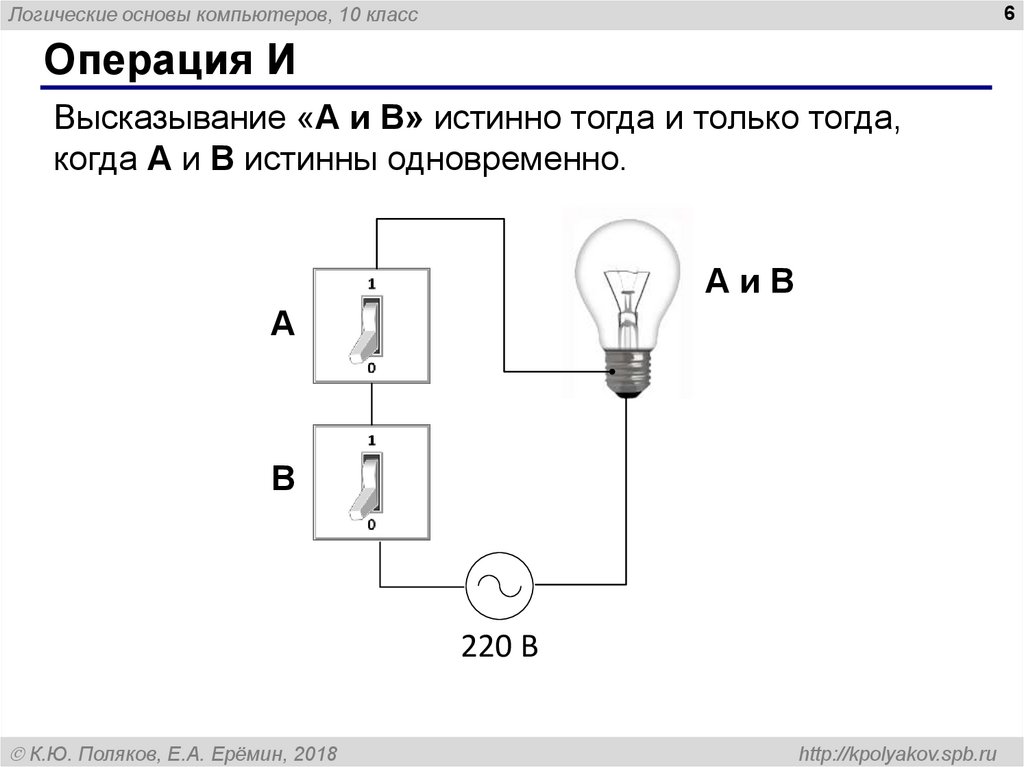
Операция И
Высказывание «A и B» истинно тогда и только тогда,
когда А и B истинны одновременно.
AиB
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
7. Операция И (логическое умножение, конъюнкция)
Логические основы компьютеров, 10 класс7
Операция И (логическое умножение, конъюнкция)
0
1
2
3
A
B
АиB
0
0
1
1
0
1
0
1
0
0
0
1
также: A·B, A B,
A and B (Паскаль),
A && B (Си)
A B
конъюнкция – от лат. conjunctio — соединение
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
8. Операция ИЛИ (логическое сложение, дизъюнкция)
Логические основы компьютеров, 10 класс8
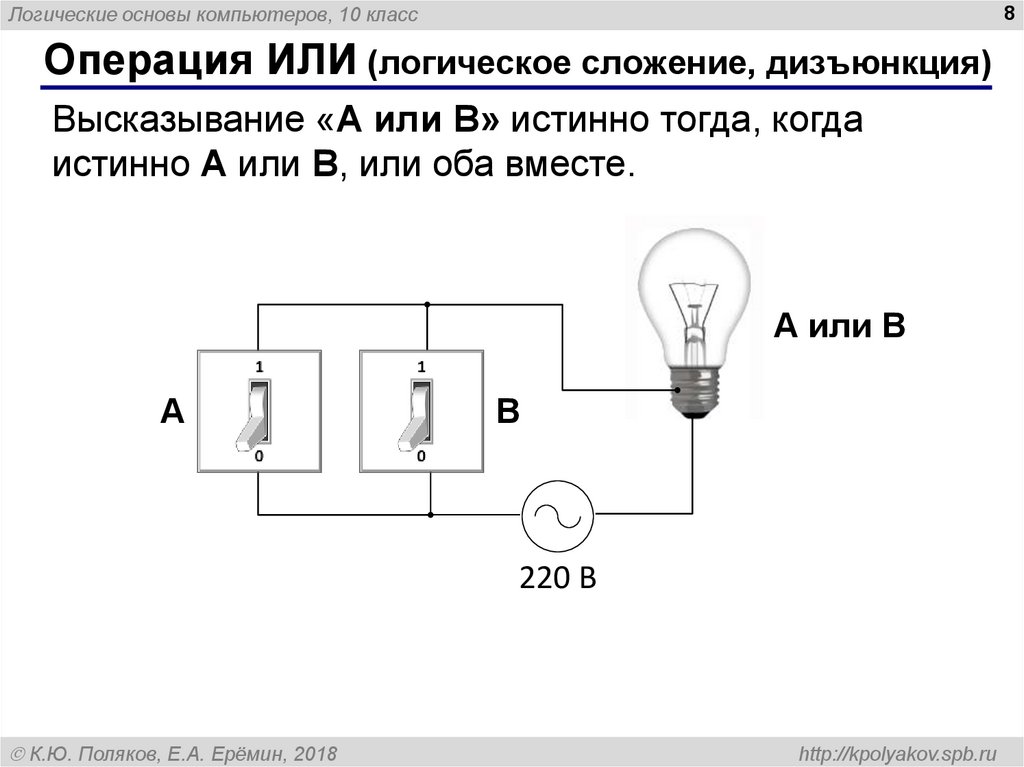
Операция ИЛИ (логическое сложение, дизъюнкция)
Высказывание «A или B» истинно тогда, когда
истинно А или B, или оба вместе.
A или B
A
B
220 В
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
9. Операция ИЛИ (логическое сложение, дизъюнкция)
Логические основы компьютеров, 10 класс9
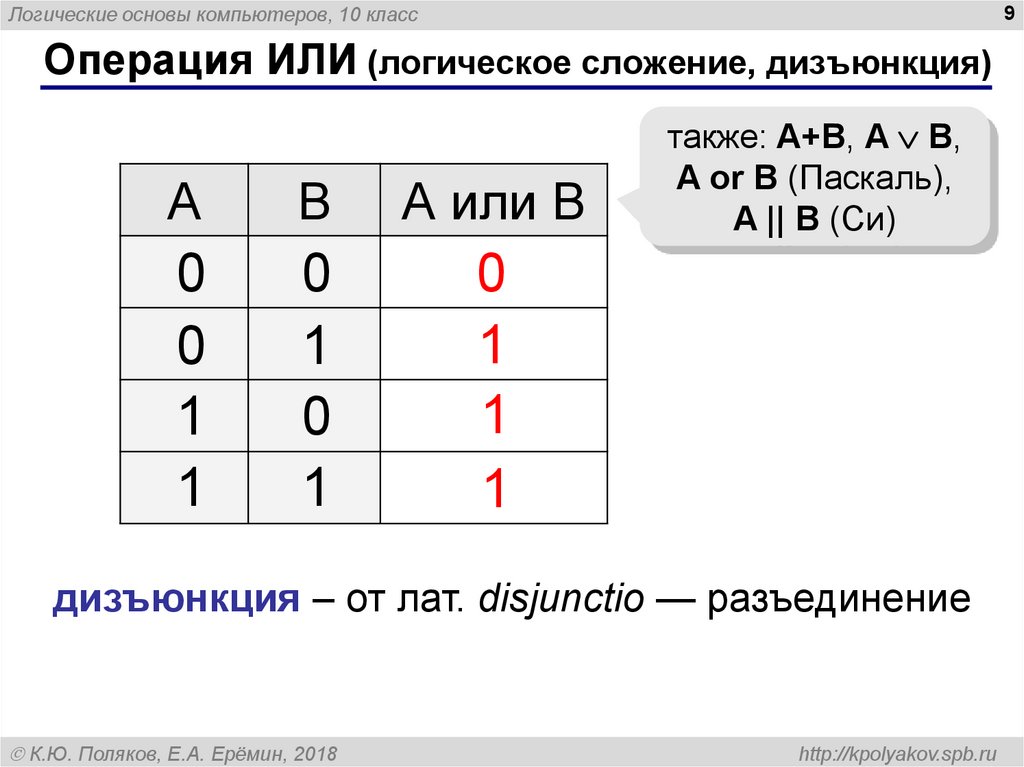
Операция ИЛИ (логическое сложение, дизъюнкция)
A
B
А или B
0
0
1
1
0
1
0
1
0
1
1
1
также: A+B, A B,
A or B (Паскаль),
A || B (Си)
дизъюнкция – от лат. disjunctio — разъединение
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
10. Операция «исключающее ИЛИ»
Логические основы компьютеров, 10 класс10
Операция «исключающее ИЛИ»
Высказывание «A B» истинно тогда, когда истинно А
или B, но не оба одновременно (то есть A B).
«Либо пан, либо пропал».
A
B
А B
0
0
1
1
0
1
0
1
0
1
1
0
также:
A xor B (Паскаль),
A ^ B (Си)
арифметическое
сложение, 1+1=2
остаток
сложение по модулю 2: А B = (A + B) mod 2
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
11. Свойства операции «исключающее ИЛИ»
Логические основы компьютеров, 10 класс11
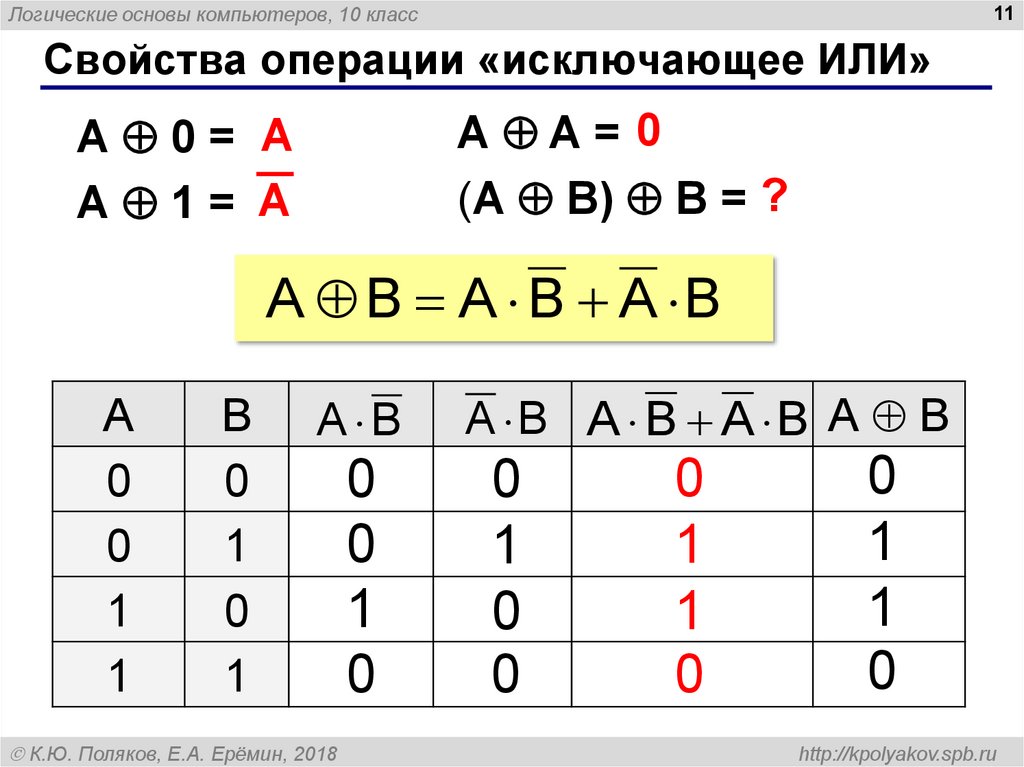
Свойства операции «исключающее ИЛИ»
A A= 0
(A B) B = ?
A 0= A
A 1= A
A B A B A B
A
0
0
1
1
B
0
1
0
1
A B
A B A B A B А B
0
0
1
0
0
1
0
0
К.Ю. Поляков, Е.А. Ерёмин, 2018
0
1
1
0
0
1
1
0
http://kpolyakov.spb.ru
12. Импликация («если …, то …»)
Логические основы компьютеров, 10 класс12
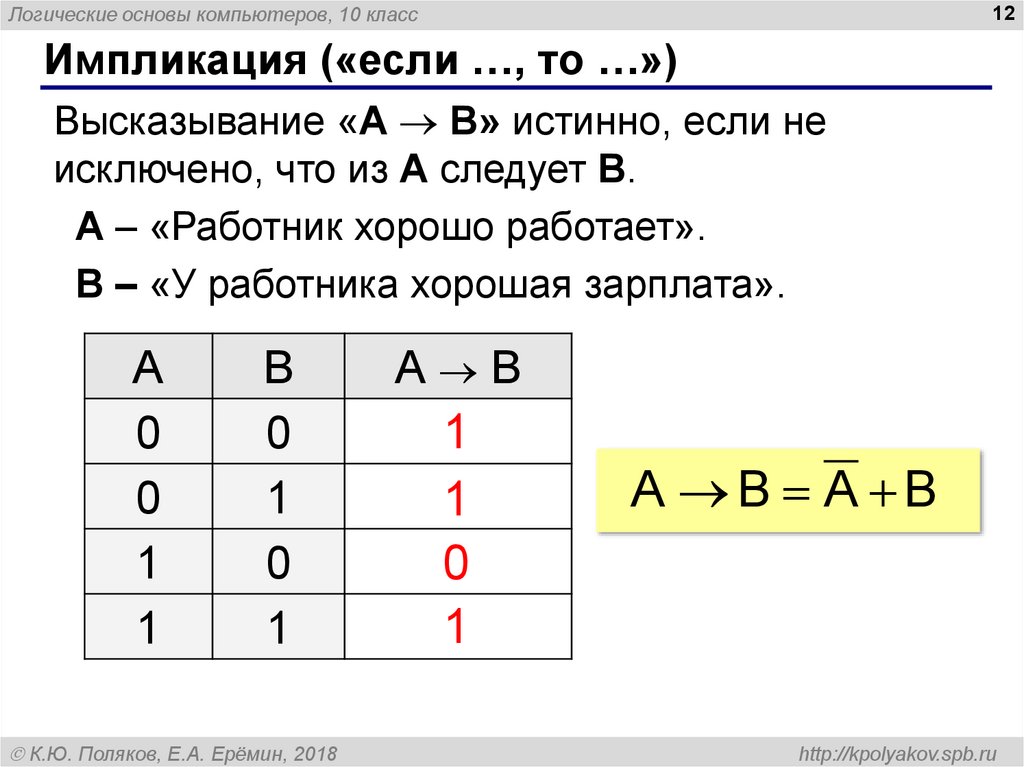
Импликация («если …, то …»)
Высказывание «A B» истинно, если не
исключено, что из А следует B.
A – «Работник хорошо работает».
B – «У работника хорошая зарплата».
A
0
0
1
1
B
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
А B
1
1
0
1
A B A B
http://kpolyakov.spb.ru
13. Импликация («если …, то …»)
Логические основы компьютеров, 10 класс13
Импликация («если …, то …»)
«Если Вася идет гулять, то Маша сидит дома».
A – «Вася идет гулять».
A
B
А
B
B – «Маша сидит дома».
A B 1
? А если Вася не идет
гулять?
0
0
1
1
0
1
0
1
1
1
0
1
Маша может пойти гулять
(B=0), а может и не пойти (B=1)!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
14. Эквиваленция («тогда и только тогда, …»)
Логические основы компьютеров, 10 класс14
Эквиваленция («тогда и только тогда, …»)
Высказывание «A B» истинно тогда и только
тогда, когда А и B равны.
A
0
0
1
1
B
0
1
0
1
А B
1
0
0
1
A B A B A B A B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
15. Базовый набор операций
Логические основы компьютеров, 10 класс15
Базовый набор операций
С помощью операций И, ИЛИ и НЕ можно
реализовать любую логическую операцию.
И
ИЛИ
НЕ
базовый набор операций
? Сколько всего существует логических операций с
двумя переменными?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
16. Логические основы компьютеров
16Логические
основы
компьютеров
§ 17. Логические выражения
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
17. Формализация
Логические основы компьютеров, 10 класс17
Формализация
Прибор имеет три датчика и может работать, если два из
них исправны. Записать в виде формулы ситуацию
«авария».
A – «Датчик № 1 неисправен».
B – «Датчик № 2 неисправен».
Формализация – это
переход к записи на
C – «Датчик № 3 неисправен».
формальном языке!
Аварийный сигнал:
X – «Неисправны два датчика».
X – «Неисправны датчики № 1 и № 2» или
«Неисправны датчики № 1 и № 3» или
«Неисправны датчики № 2 и № 3».
логическая
формула
X A B A C B C
!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
18. Вычисление логических выражений
Логические основы компьютеров, 10 класс18
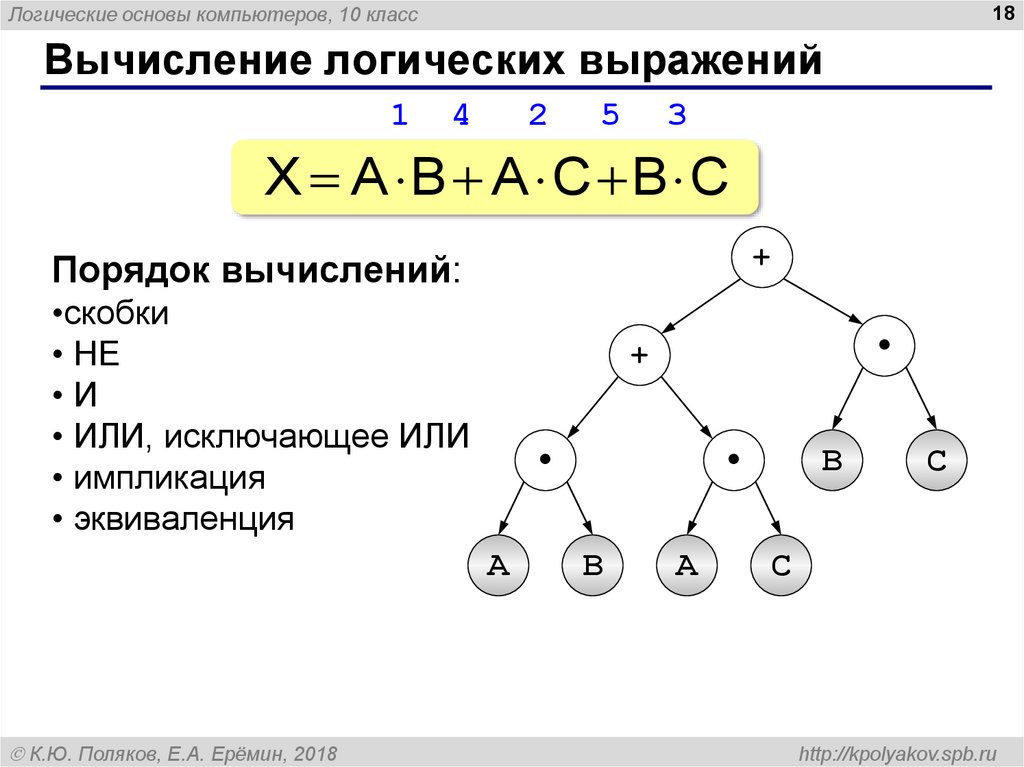
Вычисление логических выражений
1
4
2
5
3
X A B A C B C
+
Порядок вычислений:
•скобки
• НЕ
•И
• ИЛИ, исключающее ИЛИ
• импликация
• эквиваленция
A
К.Ю. Поляков, Е.А. Ерёмин, 2018
+
B
A
B
C
С
http://kpolyakov.spb.ru
19. Составление таблиц истинности
Логические основы компьютеров, 10 класс19
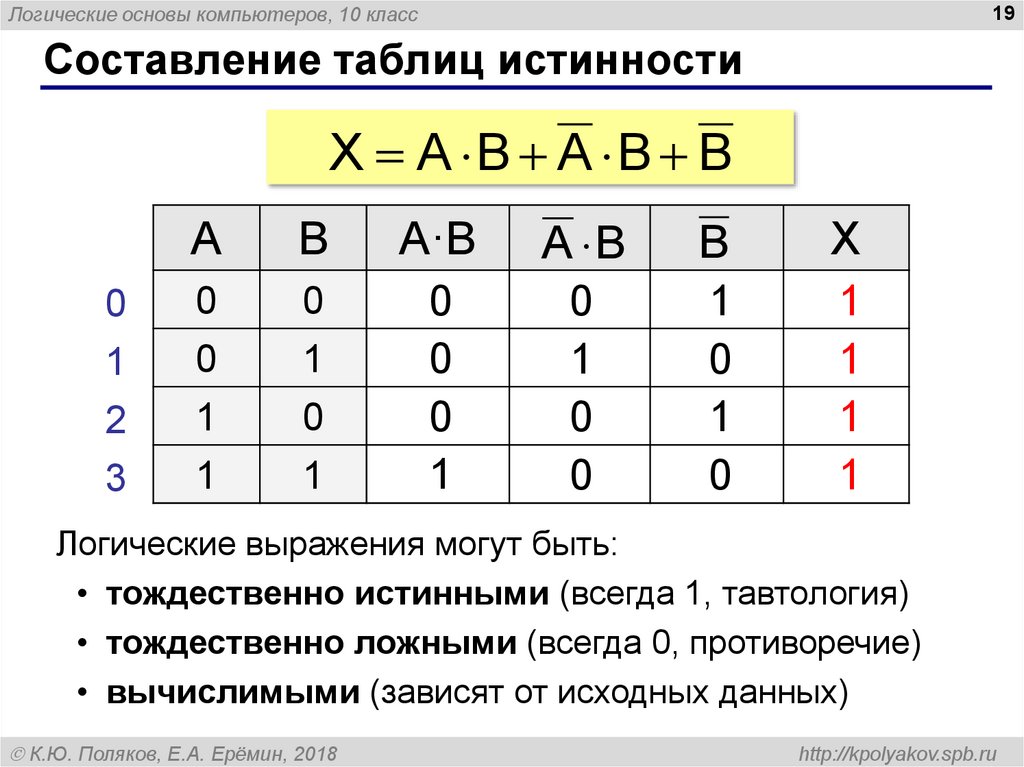
Составление таблиц истинности
X A B A B B
0
1
2
3
A
B
A·B
A B
B
X
0
0
1
1
0
1
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
1
1
Логические выражения могут быть:
• тождественно истинными (всегда 1, тавтология)
• тождественно ложными (всегда 0, противоречие)
• вычислимыми (зависят от исходных данных)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
20. Составление таблиц истинности
Логические основы компьютеров, 10 класс20
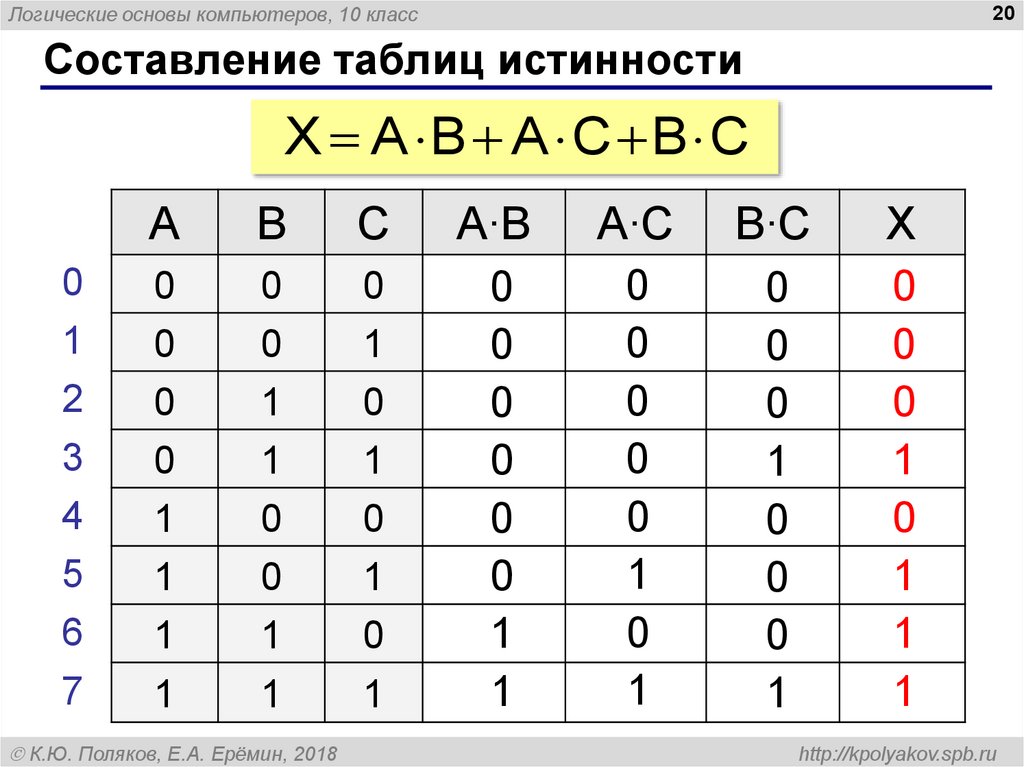
Составление таблиц истинности
X A B A C B C
0
1
2
3
4
5
6
7
A
B
C
A∙B
A∙C
B∙C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
1
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
21. Задачи
Логические основы компьютеров, 10 класс21
Задачи
Задача 1. При каких значениях логических переменных
истинно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все сомножители равны 1:
X 1 X 4 1,
X2 X3 X5 0
Задача 2. При каких значениях логических переменных
ложно выражение:
X1 X 2 X 3 X 4 X 5
Решение. Все слагаемые равны 0:
X 1 X 3 X 5 0,
К.Ю. Поляков, Е.А. Ерёмин, 2018
X2 X4 1
http://kpolyakov.spb.ru
22. Задачи
Логические основы компьютеров, 10 класс22
Задачи
Задача 3. Запишите любое логические выражение,
соответствующее таблице истинности:
в полной
23 = 8 строк
X Y Z F
Полная таблица?
?
1 0 0 1
0 0 0 0
1 1 1 0
К.Ю. Поляков, Е.А. Ерёмин, 2018
истинно при X = 1, Y = Z = 0
X Y Z 1
F X Y Z
http://kpolyakov.spb.ru
23. Задачи
Логические основы компьютеров, 10 класс23
Задачи
Задача 4. Запишите любое логические выражение,
соответствующее таблице истинности:
X
1
0
1
Y
0
0
1
Z
0
0
1
F
0
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
ложно при X = 1, Y = Z = 0
X Y Z 0
F X Y Z
http://kpolyakov.spb.ru
24. Задачи
Логические основы компьютеров, 10 класс24
Задачи
Задача 5. Символом F обозначено одно
из указанных ниже логических
выражений от трёх аргументов: X, Y, Z.
Дан фрагмент таблицы истинности
выражения F. Какое выражение
соответствует F?
1) X Y Z
1) ¬X ¬Y ¬Z
2) X Y Z
2) X Y Z
3) X Y Z
3) X Y Z
4) X Y Z
4) ¬X ¬Y ¬Z
X Y
1 0
0 0
1 1
Z
0
0
1
F
1
1
0
Быстрый способ:
F X Y Z
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
25. Задачи
Логические основы компьютеров, 10 класс25
Задачи
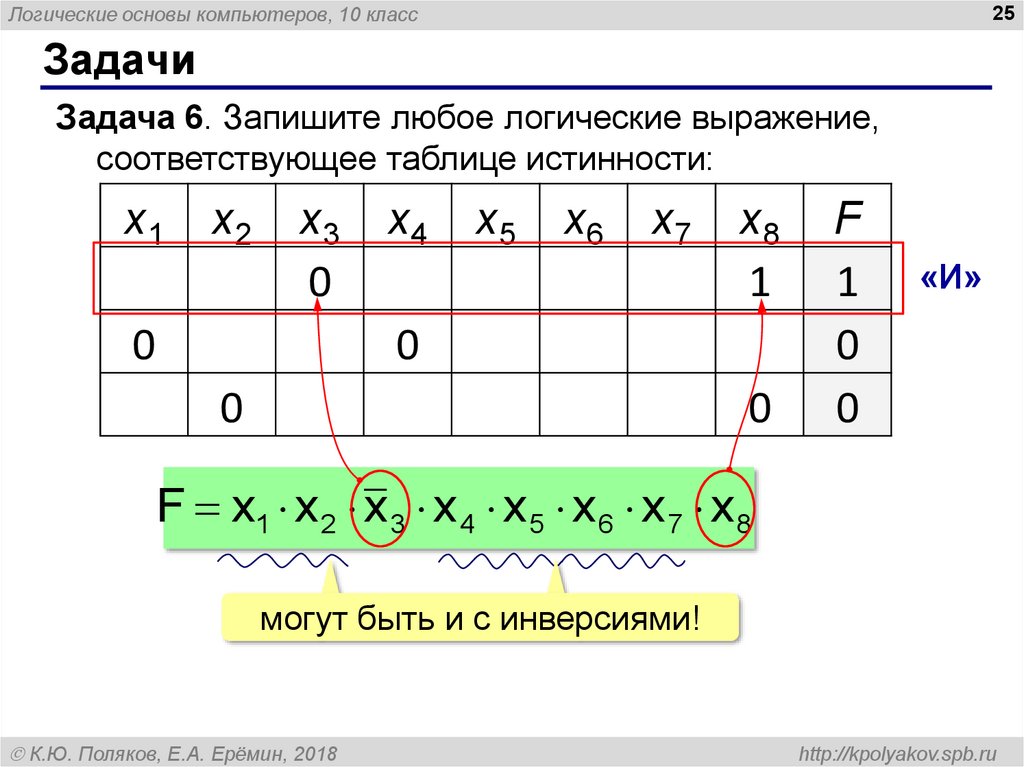
Задача 6. Запишите любое логические выражение,
соответствующее таблице истинности:
x1
x2
x3
0
0
x4
x5
x6
x7
x8
1
0
0
0
F
1
0
0
«И»
F x1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
могут быть и с инверсиями!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
26. Задачи
Логические основы компьютеров, 10 класс26
Задачи
Задача 7. Запишите любое логические выражение,
соответствующее таблице истинности:
x1
x2
x3
1
0
x4
x5
x6
x7
x8
0
F
0
1
1
0
0
0
«ИЛИ»
F x1 x 2 x 3 x 4 x 5 x 6 x 7 x 8
могут быть и с инверсиями!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
27. Задачи
Логические основы компьютеров, 10 класс27
Задачи
Задача 7. Задана таблица истинности логической
функции F Z X X Y . Определите, где какой
столбец.
Z Y
?
? X
? F
X Y Z
0 0 0 0
0 0 0
0 0 1 1
0 0 1
0 1 0 0
0 1 0
0 1 1 1
0 1 1
1 0 0 0
1 0 0
X Y Z F
1 0 1 0
1 0 0 1
1 0 1
1 1 0 0
1 1 0 1
1 1 0
1 1 1 1
1 1 1 1
1 1 1
К.Ю. Поляков, Е.А. Ерёмин, 2018
F
1
1
1
http://kpolyakov.spb.ru
28. Диаграммы Венна (круги Эйлера)
Логические основы компьютеров, 10 класс28
Диаграммы Венна (круги Эйлера)
A
A
A
B
B
A·B
A
A+B
A
A
A
B
B
A B
К.Ю. Поляков, Е.А. Ерёмин, 2018
A B
B
A B
http://kpolyakov.spb.ru
29. Диаграмма с тремя переменными
Логические основы компьютеров, 10 класс29
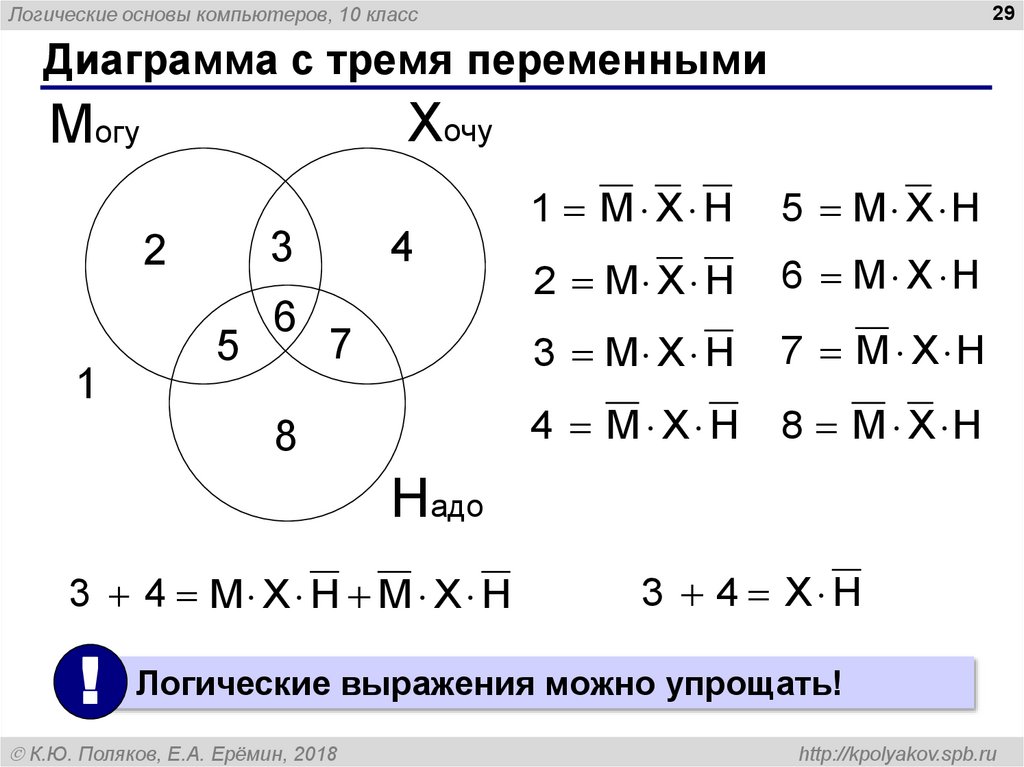
Диаграмма с тремя переменными
Хочу
Могу
3
2
1
5
6
4
7
8
1 M X H
5 M X H
2 M X H
6 M X H
3 M X H
7 M X H
4 M X H
8 M X H
Надо
3 4 M X H M X H
3 4 X H
! Логические выражения можно упрощать!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
30. Диаграмма с тремя переменными
Логические основы компьютеров, 10 класс30
Диаграмма с тремя переменными
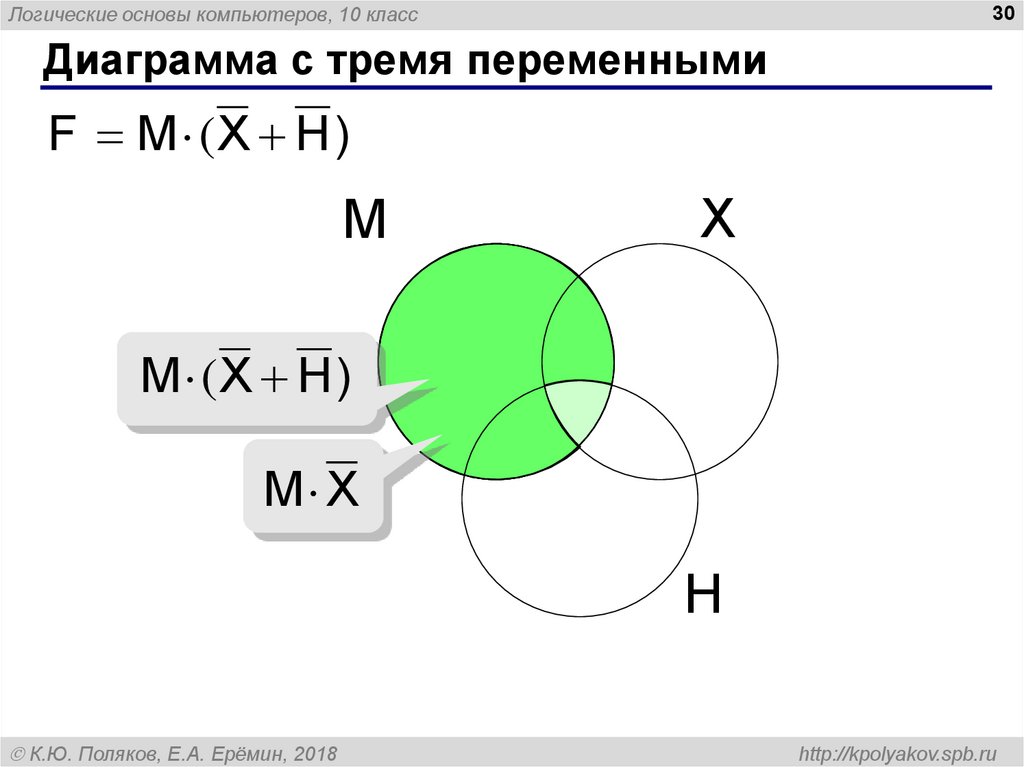
F M (X H)
М
Х
M ( X H )
M X
Н
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
31. Диаграмма с тремя переменными
Логические основы компьютеров, 10 класс31
Диаграмма с тремя переменными
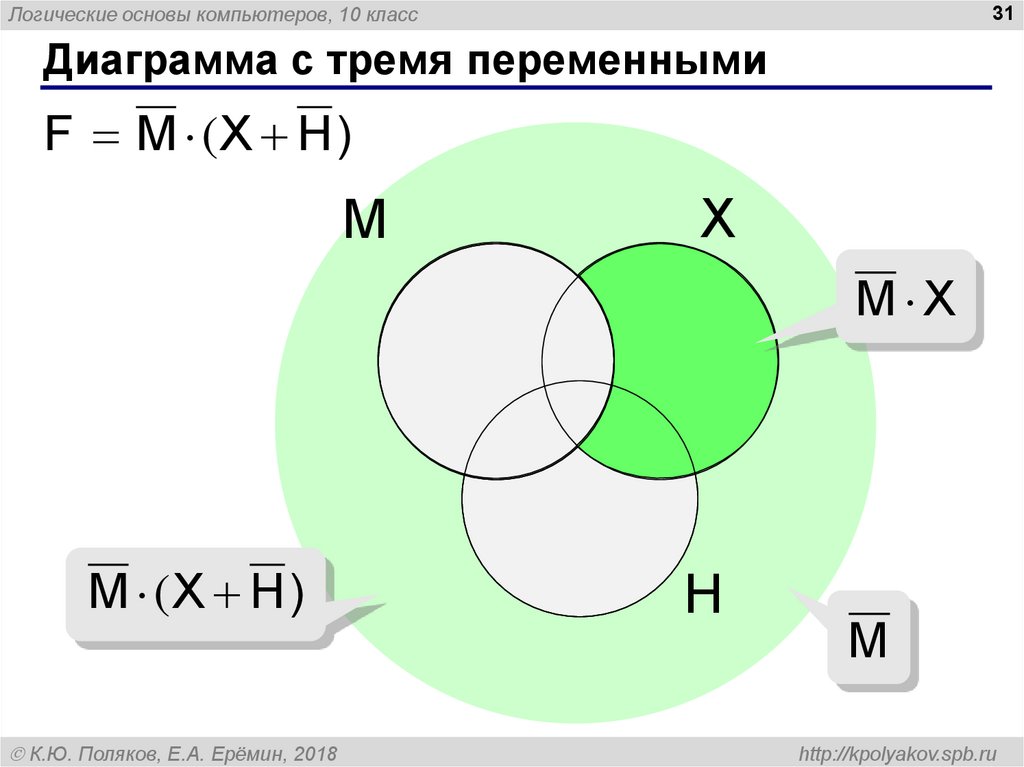
F M (X H)
М
Х
M X
M (X H)
К.Ю. Поляков, Е.А. Ерёмин, 2018
Н
M
http://kpolyakov.spb.ru
32. Задачи
Логические основы компьютеров, 10 класс32
Задачи
Известно количество сайтов, которых находит поисковый
сервер по следующим запросам:
Запрос
огурцы
помидоры
огурцы & помидоры
Количество сайтов
100
200
50
Сколько сайтов будет найдено по запросу
огурцы | помидоры
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
33. Задачи
Логические основы компьютеров, 10 класс33
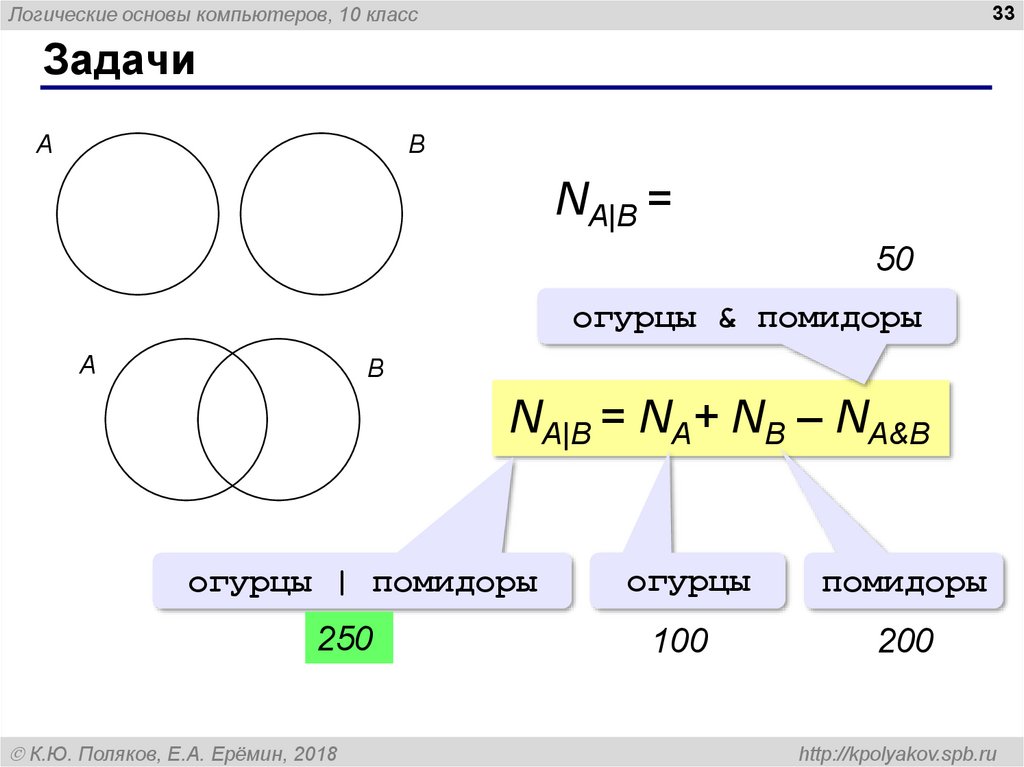
Задачи
A
B
NA|B = NA+ NB
50
огурцы & помидоры
A
B
NA|B = NA+ NB – NA&B
огурцы | помидоры
огурцы
помидоры
250
100
200
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
34. Задачи
Логические основы компьютеров, 10 класс34
Задачи
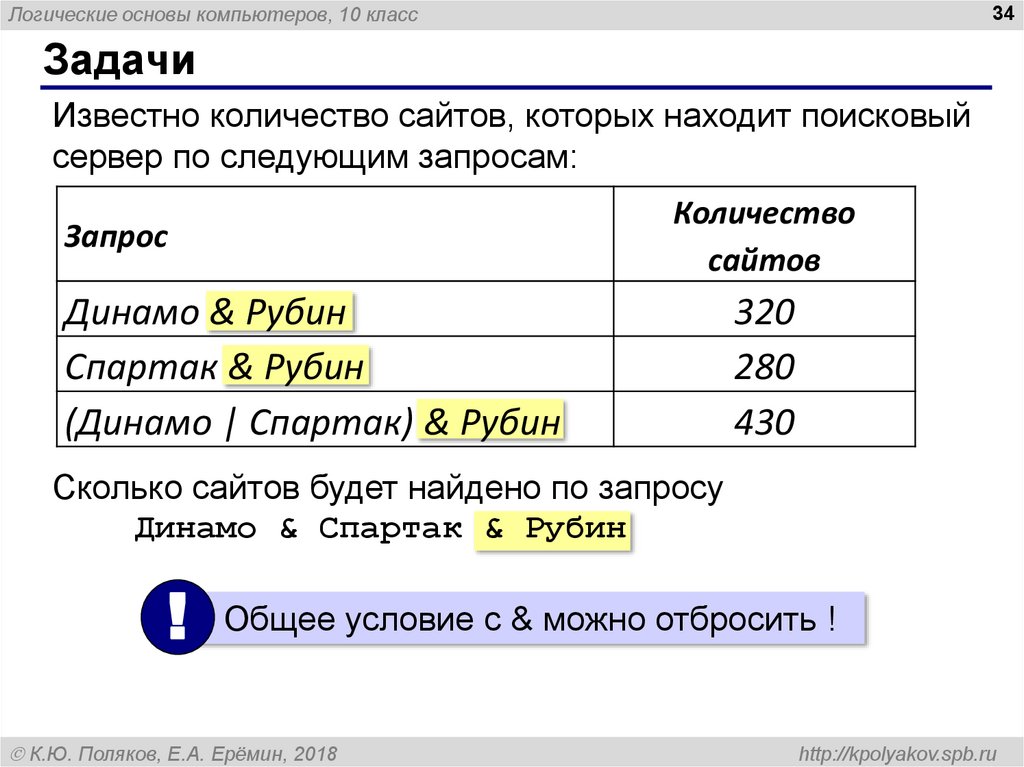
Известно количество сайтов, которых находит поисковый
сервер по следующим запросам:
Запрос
Количество
сайтов
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак & Рубин
! Общее условие с & можно отбросить !
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
35. Задачи
Логические основы компьютеров, 10 класс36
Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
Динамо
Спартак
Динамо | Спартак
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак
Ответ: 320 + 280 – 430 = 170
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
36. Задачи
Логические основы компьютеров, 10 класс38
Задачи
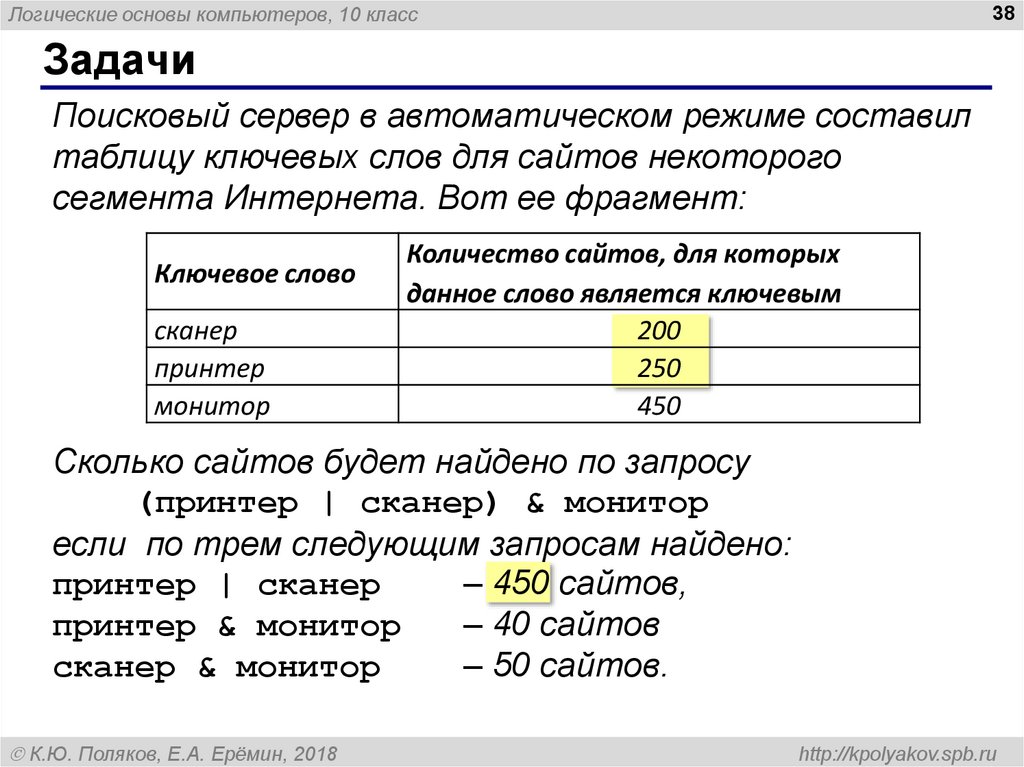
Поисковый сервер в автоматическом режиме составил
таблицу ключевых слов для сайтов некоторого
сегмента Интернета. Вот ее фрагмент:
Ключевое слово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если по трем следующим запросам найдено:
принтер | сканер
– 450 сайтов,
принтер & монитор
– 40 сайтов
сканер & монитор
– 50 сайтов.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
37. Задачи
Логические основы компьютеров, 10 класс39
Задачи
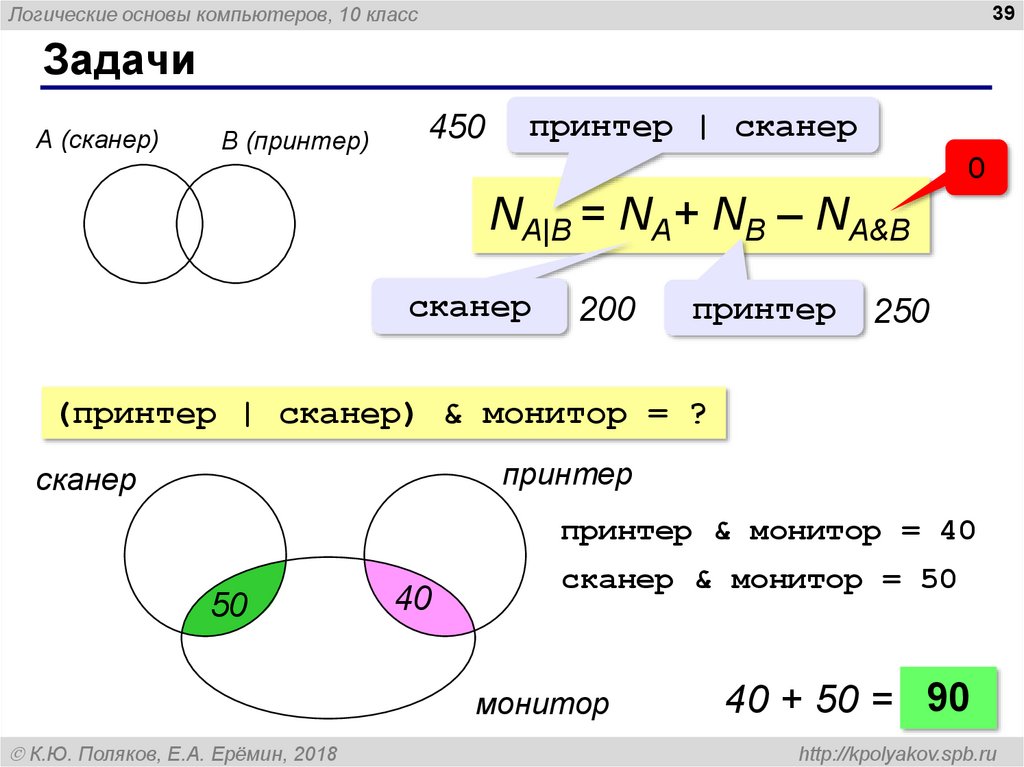
А (сканер)
B (принтер)
450
принтер | сканер
0
NA|B = NA+ NB – NA&B
сканер
200
принтер
250
(принтер | сканер) & монитор = ?
принтер
сканер
принтер & монитор = 40
50
40
сканер & монитор = 50
монитор
К.Ю. Поляков, Е.А. Ерёмин, 2018
40 + 50 = 90
http://kpolyakov.spb.ru
38. Задачи
Логические основы компьютеров, 10 класс40
Сложная задача
Ниже приведены запросы и количество страниц, которые нашел
поисковый сервер по этим запросам в некотором сегменте
Интернета:
мезозой
500
кроманьонец
600
неандерталец
700
мезозой | кроманьонец
800
мезозой | неандерталец
1000
неандерталец & (мезозой | кроманьонец) 200
Сколько страниц будет найдено по запросу
кроманьонец & (мезозой | неандерталец)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
39. Задачи
41Логические
основы
компьютеров
§ 21. Упрощение логических
выражений
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
40. Сложная задача
Логические основы компьютеров, 10 класс42
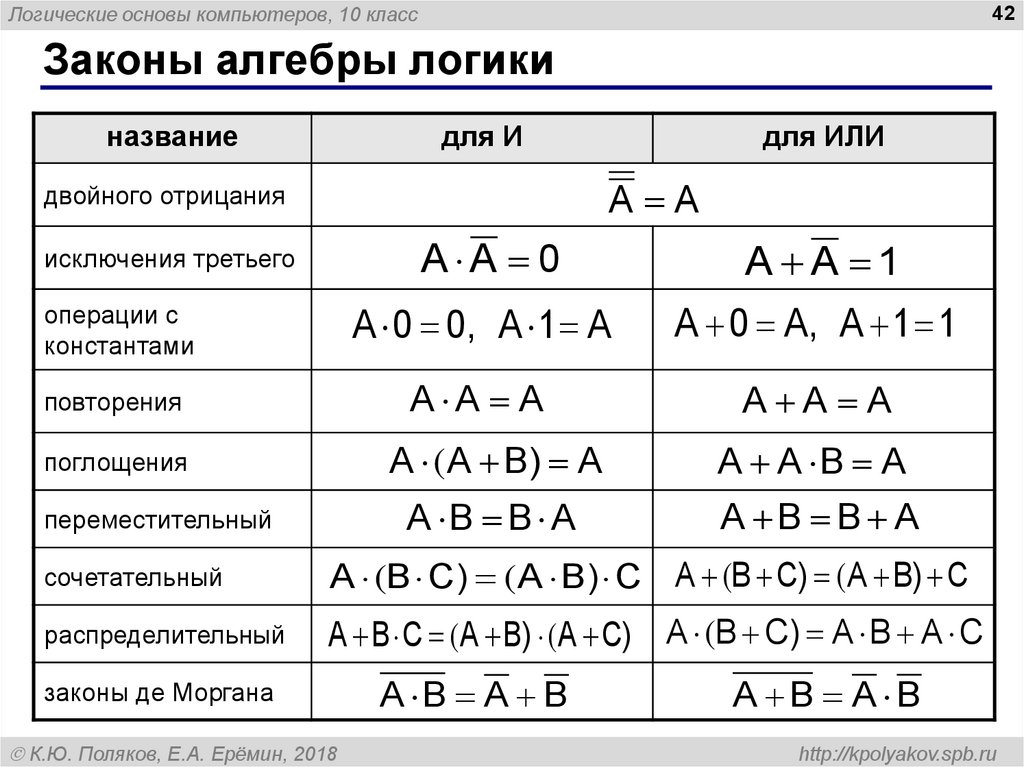
Законы алгебры логики
название
для И
для ИЛИ
A A
двойного отрицания
A A 0
A A 1
операции с
константами
A 0 0, A 1 A
A 0 A, A 1 1
повторения
A A A
A A A
поглощения
A ( A B) A
A A B A
переместительный
A B B A
A B B A
исключения третьего
сочетательный
A (B C) ( A B) C A (B C) ( A B) C
распределительный
A B C ( A B) ( A C) A (B C) A B A C
законы де Моргана
К.Ю. Поляков, Е.А. Ерёмин, 2018
A B A B
A B A B
http://kpolyakov.spb.ru
41. Логические основы компьютеров
Логические основы компьютеров, 10 класс43
Упрощение логических выражений
Шаг 1. Заменить операции на их выражения
через И, ИЛИ и НЕ:
A B A B A B
A B A B
A B A B A B
Шаг 2. Раскрыть инверсию сложных выражений по
формулам де Моргана:
A B A B,
A B A B
Шаг 3. Используя законы логики, упрощать выражение,
стараясь применять закон исключения третьего.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
42. Законы алгебры логики
Логические основы компьютеров, 10 класс44
Упрощение логических выражений
Q M X H M X H (M M ) X H X H
X (B A) (A B) (A C)
( B A) (A B) (A C)
формула де Моргана
( B A) A B (A C)
( B A A A ) B (A C)
B A B (A C)
B A (A C)
B A
раскрыли
распределительный
исключения третьего
повторения
поглощения
? Как сделать проще?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
43. Упрощение логических выражений
Логические основы компьютеров, 10 класс45
Примеры:
F (A P ) ( Q A)
Ответ: F A P Q
F P (Q A P )
Ответ: F P Q A
F (A Q) P ((A Q ) ( Q A Q P))
Ответ: F A Q P
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
44. Упрощение логических выражений
Логические основы компьютеров, 10 класс46
Задачи (упрощение)
Какое логическое выражение равносильно выражению
A ¬(¬B C)?
1) A B C
1) ¬A ¬B ¬C
2) A B C
2) A ¬B ¬C
3) A B C
3) A B ¬C
4) A B C
4) A ¬B C
A ( B C) A B C A B C
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
45. Примеры:
47Логические
основы
компьютеров
Логические функции
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
46. Задачи (упрощение)
Логические основы компьютеров, 10 класс48
Вспомним известное…
Логическое выражение — это символическая
запись высказывания, которая может
содержать логические переменные и знаки
логических операций.
Логическая функция — это правило
преобразования входных логических значений
в выходные. Логическая функция задаётся
таблицей истинности.
Выражения:
A
A+A B
A (A+B)
К.Ю. Поляков, Е.А. Ерёмин, 2018
A
0
0
1
1
B
0
1
0
1
F
0
0
1
1
функция
http://kpolyakov.spb.ru
47. Логические основы компьютеров
Логические основы компьютеров, 10 класс49
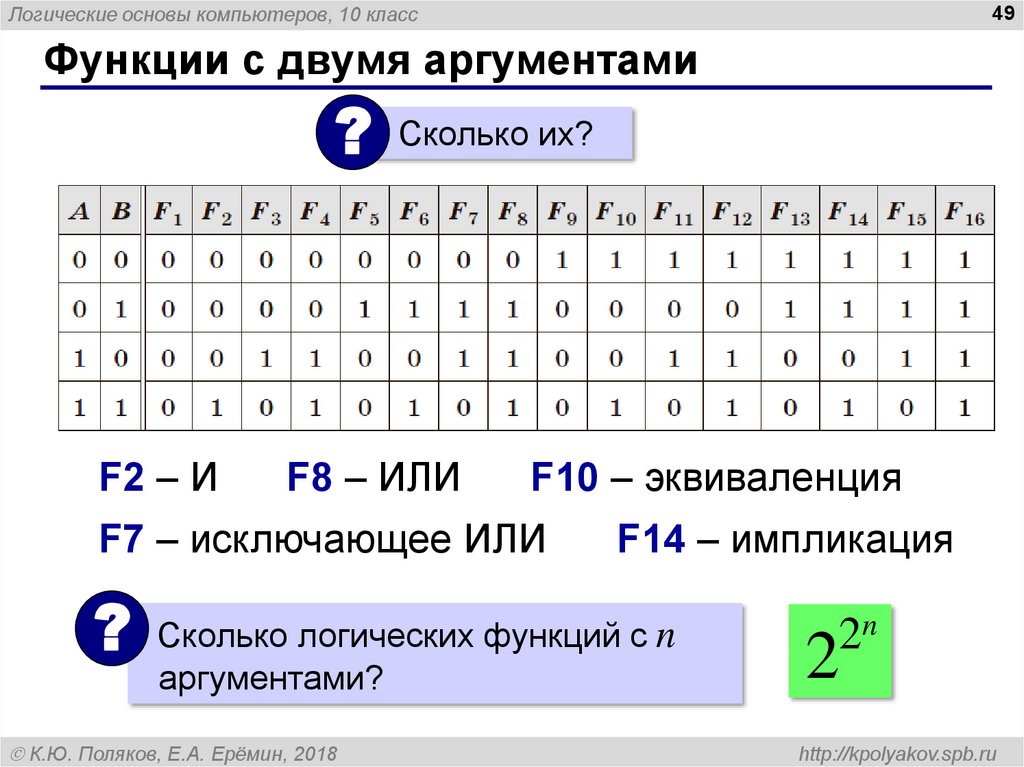
Функции с двумя аргументами
? Сколько их?
F2 – И
F8 – ИЛИ
F10 – эквиваленция
F7 – исключающее ИЛИ
F14 – импликация
? Сколько логических функций с n
аргументами?
К.Ю. Поляков, Е.А. Ерёмин, 2018
2n
2
http://kpolyakov.spb.ru
48. Вспомним известное…
Логические основы компьютеров, 10 класс50
Штрих Шеффера, «И-НЕ»
A | B A B
A
0
0
1
1
B
0
1
0
1
А|B
1
1
1
0
Базовые операции через «И-НЕ»:
A A|A
A B A | B (A | B) | (A | B)
A B A | B (A | A) | (B | B)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
49. Функции с двумя аргументами
Логические основы компьютеров, 10 класс51
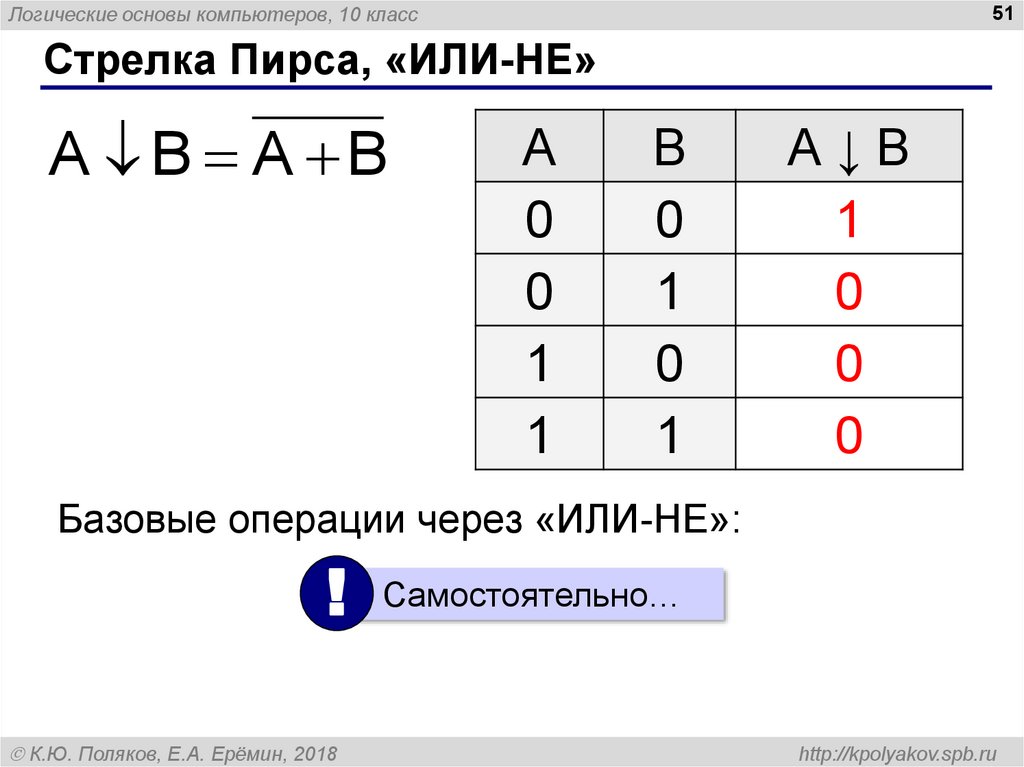
Стрелка Пирса, «ИЛИ-НЕ»
A B A B
A
0
0
1
1
B
0
1
0
1
А↓B
1
0
0
0
Базовые операции через «ИЛИ-НЕ»:
! Самостоятельно…
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
50. Штрих Шеффера, «И-НЕ»
52Логические
основы
компьютеров
§ 19. Логические уравнения
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
51. Стрелка Пирса, «ИЛИ-НЕ»
Логические основы компьютеров, 10 класс53
Логические уравнения
? Как решать?
((B C) A) ( A C D) 0
Способ 1. Построить таблицу истинности…
16 строк!
Способ 2. Свойство импликации:
(B C) A 1, A = 1 A C D 0
B C A 1 B = C = 0
D=0
Способ 3. Упрощение:
( B C A) ( A C D) 0
B C A ( A C D) 0
B C A A C D 0
B C A D 0
К.Ю. Поляков, Е.А. Ерёмин, 2018
A=1
B=C=D=0
http://kpolyakov.spb.ru
52. Логические основы компьютеров
Логические основы компьютеров, 10 класс54
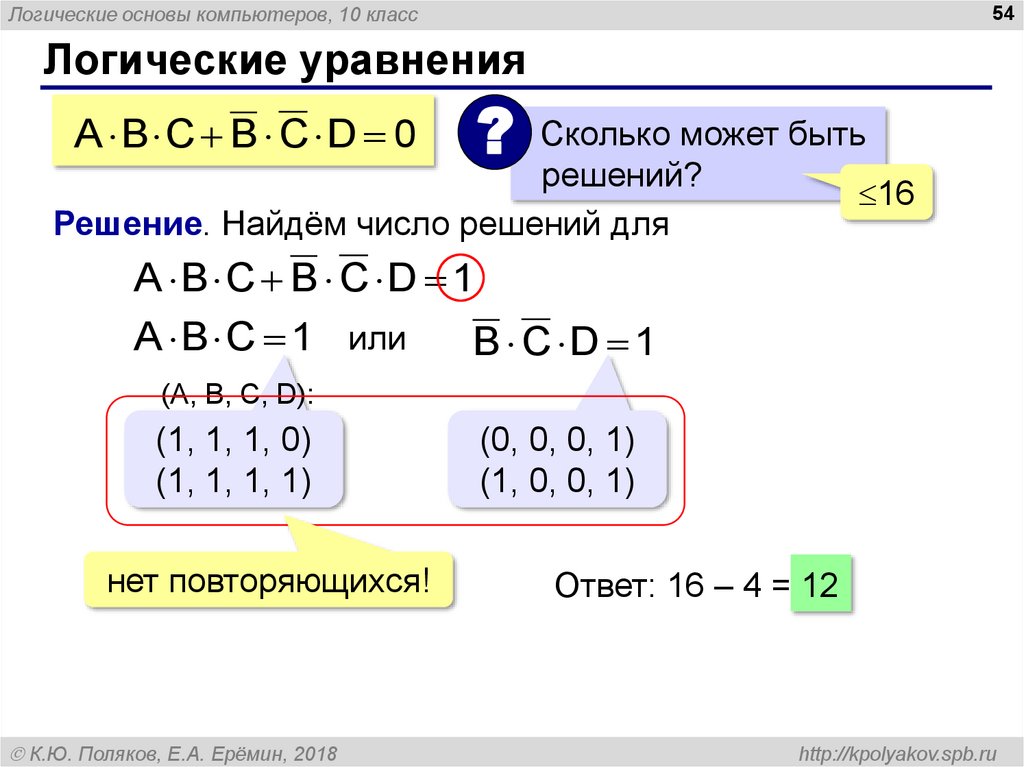
Логические уравнения
A B C B C D 0
? Сколько может быть
решений?
Решение. Найдём число решений для
16
A B C B C D 1
A B C 1 или
B C D 1
(A, B, C, D):
(1, 1, 1, 0)
(1, 1, 1, 1)
нет повторяющихся!
К.Ю. Поляков, Е.А. Ерёмин, 2018
(0, 0, 0, 1)
(1, 0, 0, 1)
Ответ: 16 – 4 = 12
http://kpolyakov.spb.ru
53. Логические уравнения
Логические основы компьютеров, 10 класс55
Логические уравнения
x1 x2 x3 x4 x5 0
00000
Запрещены 1!
x1 x2 x3 x4 x5 1
Ответ: 31
x1 x2 x3 x4 x5 1
Запрещены 0!
x1 x2 x3 x4 x5 0
? Сколько
решений?
11111
? Сколько
решений?
Ответ: 31
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
54. Логические уравнения
Логические основы компьютеров, 10 класс56
Логические уравнения
( x1 x2 ) ( x3 x4 ) 1
Запрещены 00** и **00!
x1 x2 x3 x4
пары битов:
3 3
0101 1001 1101
0110 1010 1110
0111 1011 1111
9 решений!
3
01, 10, 11
( x1 x2 ) ( x3 x4 ) 0
4 переменные – всего 24 = 16 вариантов
для уравнения с 1 в правой части – 9 решений
16 – 9 = 7 решений!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
55. Логические уравнения
Логические основы компьютеров, 10 класс57
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
? Сколько может быть
Решение:
решений?
64
Пусть x1 = 0, тогда…
x1 = x2 = x3 = x4 = x5 = x6 = 0
Пусть x1 = 1, тогда…
x1 = x2 = x3 = x4 = x5 = x6 = 1
Ответ: 2 решения,
000000 и 111111
( x1 ~ x2 ) ( x2 ~ x3 ) ( x3 ~ x4 ) ( x4 ~ x5 ) ( x5 ~ x6 ) 0
? Сколько решений?
К.Ю. Поляков, Е.А. Ерёмин, 2018
62
http://kpolyakov.spb.ru
56. Логические уравнения
Логические основы компьютеров, 10 класс58
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
Решение:
Пусть x1 = 0, тогда…
x1 = 0, x2 = 1, x3 = 0, x4 = 1, x5 = 0, x6 = 1
Пусть x1 = 1, тогда…
x1 = 1, x2 = 0, x3 = 1, x4 = 0, x5 = 1, x6 = 0
Ответ: 2 решения,
010101 и 101010
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 0
? Сколько решений?
К.Ю. Поляков, Е.А. Ерёмин, 2018
62
http://kpolyakov.spb.ru
57. Логические уравнения
Логические основы компьютеров, 10 класс59
Логические уравнения
( x1 x2 ) ( x2 x3 ) ( x3 x4 ) ( x4 x5 ) ( x5 x6 ) 1
? Когда нарушится?
Решение:
Рассмотрим цепочку x1 x2 x3 x4 x5 x6
1 0
! После 1 могут быть только 1!
Ответ: 000000
000001
000011
000111
001111
011111
111111
К.Ю. Поляков, Е.А. Ерёмин, 2018
7 решений
Для уравнения с N переменными:
N+1 решений.
http://kpolyakov.spb.ru
58. Логические уравнения
Логические основы компьютеров, 10 класс60
Системы логических уравнений
( x1 x2 ) ( x2 x3 ) ... ( x5 x6 ) 1
7 решений
( y1 y2 ) ( y2 y3 ) ... ( y4 y5 ) 1 6 решений
! Уравнения независимы!
всего 7 6 = 42 решения!
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
59. Логические уравнения
Логические основы компьютеров, 10 класс61
Системы логических уравнений
( x1 x2 ) ( x2 x3 ) ... ( x5 x6 ) 1
7 решений
( y1 y2 ) ( y2 y3 ) ... ( y4 y5 ) 1 6 решений
y 2 x4 1
уравнение связи
y2 0 x4 {0, 1} X:
000000
y2 1 x4 1
000001
всего 7 4 + 4 2
= 36 решений!
К.Ю. Поляков, Е.А. Ерёмин, 2018
000011
000111
001111
011111
111111
Y:
00000 7
00001 7
00011 7
00111 7
01111 4
11111 4
http://kpolyakov.spb.ru
60. Системы логических уравнений
Логические основы компьютеров, 10 класс62
Системы логических уравнений
( x1 y1 ) ( x2 y2 )
( x2 y2 ) ( x3 y3 )
...
( x8 y8 ) ( x9 y9 )
Замена переменных:
z1 ( x1 y1 )
z2 ( x2 y2 )
…
z9 ( x9 x9 )
z1 z2 , z2 z3, z8 z9
z1 z2 , z2 z3, z8 z9
( z1 z2 ) ( z2 z3 ) ( z2 z3 ) ( z8 z9 ) 1
!
Биты чередуются!
К.Ю. Поляков, Е.А. Ерёмин, 2018
Решения: Z = 010101010,
Z = 101010101
http://kpolyakov.spb.ru
61. Системы логических уравнений
Логические основы компьютеров, 10 класс63
Системы логических уравнений
Решения: Z = 010101010,
Z = 101010101
zi ( xi yi )
9 битов
zi 0 ( xi , yi ) (0,1) (1,0)
zi 1 ( xi , yi ) (0,0) (1,1)
!
0 и 1 дают по
2 решения!
29 + 29 = 1024
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
62. Системы логических уравнений
Логические основы компьютеров, 10 класс64
Системы логических уравнений
( x1 y1 ) ( x2 y2 )
( x2 y2 ) ( x3 y3 )
...
( x5 y5 ) ( x6 y6 )
Замена переменных:
z1 ( x1 y1 )
z 2 ( x2 y 2 )
z6 ( x6 y6 )
( z1 z2 ) ( z2 z3 ) ( z5 z6 ) 1
«биты чередуются»
Решения: 010101, 101010
zi 1 ( xi , yi ) (1,1)
Ответ: 33+33= 54
zi 0 ( xi , yi ) (0,0)(0,1)(1,0)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
63. Системы логических уравнений
65Логические
основы
компьютеров
§ 20. Синтез логических
выражений
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
64. Системы логических уравнений
Логические основы компьютеров, 10 класс66
Синтез логических выражений
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 1.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат.
распределительный
X A B A B A B A (B B) A B
A A B ( A A) ( A B) A B
исключения
третьего
распределительный
К.Ю. Поляков, Е.А. Ерёмин, 2018
исключения
третьего
http://kpolyakov.spb.ru
65. Логические основы компьютеров
Логические основы компьютеров, 10 класс67
Синтез логических выражений (2 способ)
A B
X
0
0
1
1
1
1
0
1
0
1
0
1
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое истинно
только для этой строки.
Шаг 3. Сложить эти выражения и
упростить результат, который
равен X .
Шаг 4. Сделать инверсию.
X A B X A B A B
? Когда удобнее применять 2-ой способ?
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
66. Синтез логических выражений
Логические основы компьютеров, 10 класс68
Синтез логических выражений (3 способ)
A B
X
0
0
1
1
0
1
0
1
0
1
0
1
A B
A B
Шаг 1. Отметить строки в
таблице, где X = 0.
Шаг 2. Для каждой из них
записать логическое
выражение, которое ложно
только для этой строки.
Шаг 3. Перемножить эти
выражения и упростить
результат.
X (A B) ( A B) A A B A A B B B
B (A A) B B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
67. Синтез логических выражений (2 способ)
Логические основы компьютеров, 10 класс69
Синтез логических выражений
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
X A B C A B C
A B C
A B C
A B C
A B C
A B C
A B C
A B C A B C
A B C A B C
A B ( C C)
A B ( C C)
A C ( B B)
A B A B A C
A (B B) A C
A A C
(A A) (A C) A C
http://kpolyakov.spb.ru
68. Синтез логических выражений (3 способ)
Логические основы компьютеров, 10 класс70
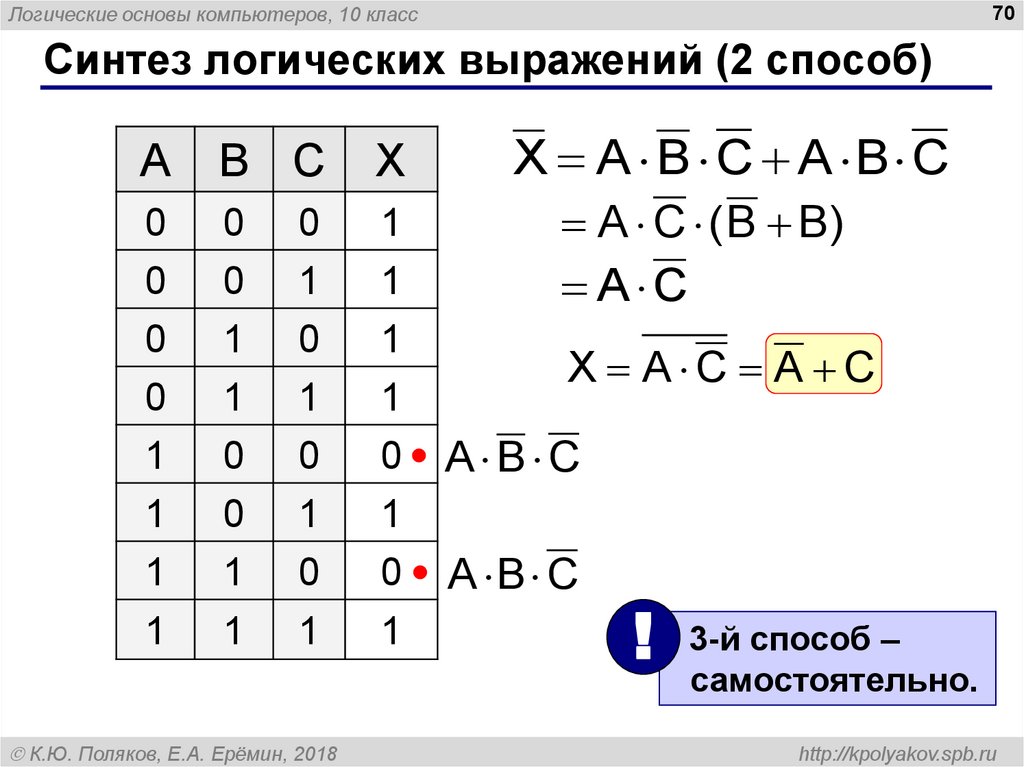
Синтез логических выражений (2 способ)
A
B C
X
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
X A B C A B C
A C ( B B)
A C
X A C A C
A B C
A B C
! 3-й способ –
самостоятельно.
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
69. Синтез логических выражений
71Логические
основы
компьютеров
§ 21. Множества и логика
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
70. Синтез логических выражений (2 способ)
Логические основы компьютеров, 10 класс72
Что нужно знать о множествах?
U – универсальное
множество
(все натуральные)
A
(делятся на 6)
A – дополнение A до
универсального множества
(НЕ делятся на 6)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
71. Логические основы компьютеров
Логические основы компьютеров, 10 класс73
Что нужно знать о множествах?
A
B
A·B – пересечение (A B)
A
B
A+B – объединение (A B)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
72. Что нужно знать о множествах?
Логические основы компьютеров, 10 класс74
Множества и логические функции
Множество задаётся логической функцией
A
x A
A(x) = 1
A
A( x) 1 x A
x A
A
B
A( x) B( x) 1 x A·B
A
B
A ( x) B( x) 1 x A+B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
73. Что нужно знать о множествах?
Логические основы компьютеров, 10 класс75
Задача дополнения (I)
Задача 1. Каким должно быть множество A для того,
чтобы множество A + B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
это решение!
B B U A B
B ( x) 1
это условие
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U Amin B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
74. Множества и логические функции
Логические основы компьютеров, 10 класс76
Задача дополнения (II)
Задача 2. Каким должно быть множество A для того,
чтобы множество A B совпадало с универсальным
множеством U?
A B U A( x) B( x) 1 для всех x
B B U A B A B
B( x ) 1
это условие
это решение!
? Есть ли другие решения?
A
определяет нужное
множество A
A включает B
(A B)
C B B U ( A ) min B
К.Ю. Поляков, Е.А. Ерёмин, 2018
A B
Amax B
http://kpolyakov.spb.ru
75. Задача дополнения (I)
Логические основы компьютеров, 10 класс77
Общий подход к решению
1. Свести задачу к одной из базовых задач
Задача 1. A B 1
B A 1
Задача 2. A B 1 B A 1
2. Использовать готовое решение:
Задача 1. Amin B
Задача 2. Amax B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
76. Задача дополнения (II)
Логические основы компьютеров, 10 класс78
Задачи с отрезками
На числовой прямой даны два отрезка:
P = [37; 60] и Q = [40; 77]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
P (Q A P )
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
77. Общий подход к решению
Логические основы компьютеров, 10 класс79
Задачи с отрезками
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = [37; 60], Q = [40; 77]
Amin = [40; 60]
К.Ю. Поляков, Е.А. Ерёмин, 2018
длина 20
http://kpolyakov.spb.ru
78. Задачи с отрезками
Логические основы компьютеров, 10 класс80
Задачи с отрезками-II
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наибольшую
возможную длину такого отрезка A, что
выражение
(x A) → ((x P) (x Q))
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
A ( P Q)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
79. Задачи с отрезками
Логические основы компьютеров, 10 класс81
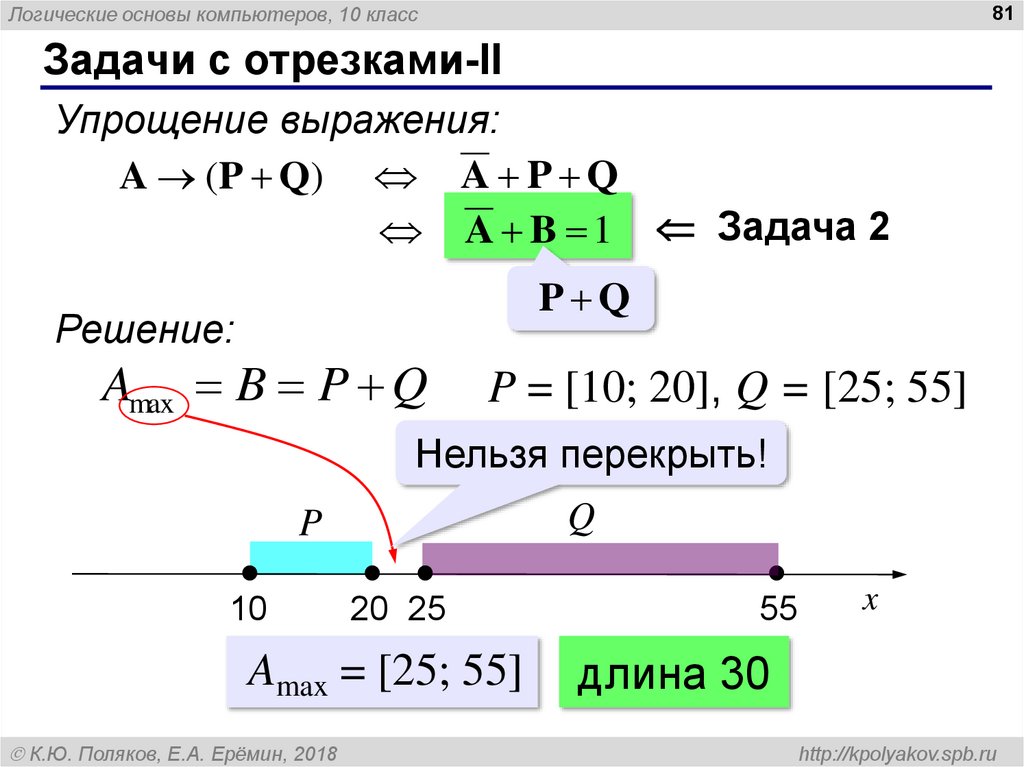
Задачи с отрезками-II
Упрощение выражения:
A ( P Q) A P Q
A B 1 Задача 2
P Q
Решение:
Amax B P Q
P = [10; 20], Q = [25; 55]
Нельзя перекрыть!
Q
P
10
20 25
Amax = [25; 55]
К.Ю. Поляков, Е.А. Ерёмин, 2018
55
x
длина 30
http://kpolyakov.spb.ru
80. Задачи с отрезками-II
Логические основы компьютеров, 10 класс82
Задачи с отрезками-III
На числовой прямой даны два отрезка:
P = [10; 20] и Q = [25; 55]. Укажите наименьшую
возможную длину такого отрезка A, что
выражение
((x P) (x Q)) → (x A)
истинно при любом значении переменной х.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
( P Q) A
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
81. Задачи с отрезками-II
Логические основы компьютеров, 10 класс83
Задачи с отрезками-III
Упрощение выражения:
( P Q) A A P Q
A B 1
Задача 1
P Q
Решение:
Amin B P Q
P
10
P = [10; 20], Q = [25; 55]
Нужно перекрыть!
Q
20 25
Amin = [10; 55]
К.Ю. Поляков, Е.А. Ерёмин, 2018
55
x
длина 45
http://kpolyakov.spb.ru
82. Задачи с отрезками-III
Логические основы компьютеров, 10 класс84
Множества чисел
Элементами множеств А, P и Q являются
натуральные числа, причём
P = {2, 4, 6, 8, 10, 12} и Q = {4, 8, 12, 116}.
Известно, что выражение
(x P) → (((x Q) ¬(x A)) → ¬(x P))
истинно при любом значении переменной х.
Определите наименьшее возможное значение суммы
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
P (Q A P )
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
83. Задачи с отрезками-III
Логические основы компьютеров, 10 класс85
Множества чисел
Упрощение выражения:
P (Q A P ) P (Q A P)
P Q A P
P Q A
A B 1 Задача 1
Решение:
P Q
Amin B P Q P Q
P = {2, 4, 6, 8, 10, 12}, Q = {4, 8, 12, 116}
Amin = {4, 8, 12}
К.Ю. Поляков, Е.А. Ерёмин, 2018
сумма 24
http://kpolyakov.spb.ru
84. Множества чисел
Логические основы компьютеров, 10 класс86
Множества чисел-II
Элементами множеств А, P и Q являются
натуральные числа, причём
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }.
Известно, что выражение
((x A) → ¬(x P)) (¬(x Q) → ¬(x A))
истинно при любом значении переменной х.
Определите наибольшее возможное количество
элементов множества A.
Вводим утверждения:
P = (x P), Q = (x Q),
A = (x A)
Заданное условие:
( A P ) ( Q A)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
85. Множества чисел
Логические основы компьютеров, 10 класс87
Множества чисел-II
Упрощение выражения:
( A P ) (Q A) ( A P) (Q A)
A Q P Q A P A
A Q P Q A
A P Q
A B 1 Задача 2
Решение:
Amax B P Q
P Q
P = { 2, 4, 6, 8, 10, 12, 14, 16, 18, 20}
Q = { 3, 6, 9, 12, 15, 18, 21, 24, 27, 30 }
Amax = { 3, 9, 15, 21, 24, 27, 30 }
К.Ю. Поляков, Е.А. Ерёмин, 2018
7 шт.
http://kpolyakov.spb.ru
86. Множества чисел-II
88Логические
основы
компьютеров
§ 22. Предикаты и кванторы
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
87. Множества чисел-II
Логические основы компьютеров, 10 класс89
Предикаты
Предикат (логическая функция) – это утверждение,
содержащее переменные.
Предикат-свойство – от одной переменной:
P(N) = «В городе N живут более 2 млн человек»
P(Москва) = 1
P(Якутск) = 0
Простое(x) = «x – простое число»
Спит(x) = «x всегда спит на уроке»
Предикат-отношение – от нескольких переменных:
Больше(x, y) = «x > y»
Живет(x, y) = «x живет в городе y»
Любит(x, y) = «x любит y»
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
88. Логические основы компьютеров
Логические основы компьютеров, 10 класс90
Предикаты и кванторы
Предикаты задают множества:
P( x ) ( x 0)
P( x, y ) ( x y 1)
Предикаты, которые всегда истинны:
2
P( x) ( x 0) для всех вещественных чисел
«Для любого допустимого x утверждение P(x)
истинно»:
квантор
x P(x )
высказывание
Квантор – знак, обозначающий количество.
А (all – все) E (exists – существует)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
89. Предикаты
Логические основы компьютеров, 10 класс91
Кванторы
Какой квантор использовать?
моря соленые».
« …
кошки серые».
« …
числа чётные».
« …
« …
окуни – рыбы».
прямоугольники – квадраты».
« …
квадраты – прямоугольники».
« …
Истинно ли высказывание?
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x) ( x 2 0)
x P(x ) при P( x) ( x 2 0)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
90. Предикаты и кванторы
Логические основы компьютеров, 10 класс92
Кванторы
Дано:
A = «Все люди смертны» = 1.
B = «Сократ – человек» = 1.
Доказать:
C = «Сократ смертен» = 1.
Доказательство:
A
0
0
B
0
1
А B
1
1
1
1
0
1
0
1
P(x) = «x – человек»
Q(x) = «x – смертен»
x (P( x ) Q( x))
A = 1:
P( Сократ ) Q( Сократ) 1
при «x =Сократ»
P( Сократ ) 1
B = 1:
по свойствам импликации Q( Сократ ) 1
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
91. Кванторы
Логические основы компьютеров, 10 класс93
Несколько кванторов
Квантор связывает одну переменную:
x P( x, y ) – предикат от переменной y
y P( x, y ) – предикат от переменной x
Два квантора связывают две переменных:
x y P( x, y ) – высказывание «для любого x
существует y, при котором P(x,y)=1»
x y P( x, y ) – высказывание «существует x, такой
что при любом y верно P(x,y)=1»
Сравните два последних высказывания при:
P( x, y ) ( x y 0)
К.Ю. Поляков, Е.А. Ерёмин, 2018
P( x, y ) ( x y 0)
http://kpolyakov.spb.ru
92. Кванторы
Логические основы компьютеров, 10 класс94
Отрицание
НЕ «для любого x выполняется P(x)»
«существует x, при котором не выполняется P(x)»
x P(x) x P(x)
НЕ «существует x, при котором выполняется P(x)»
«для любого x не выполняется P(x)»
x P(x) x P(x)
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
93. Несколько кванторов
95Логические
основы
компьютеров
§ 23. Логические элементы
компьютера
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
94. Отрицание
Логические основы компьютеров, 10 класс96
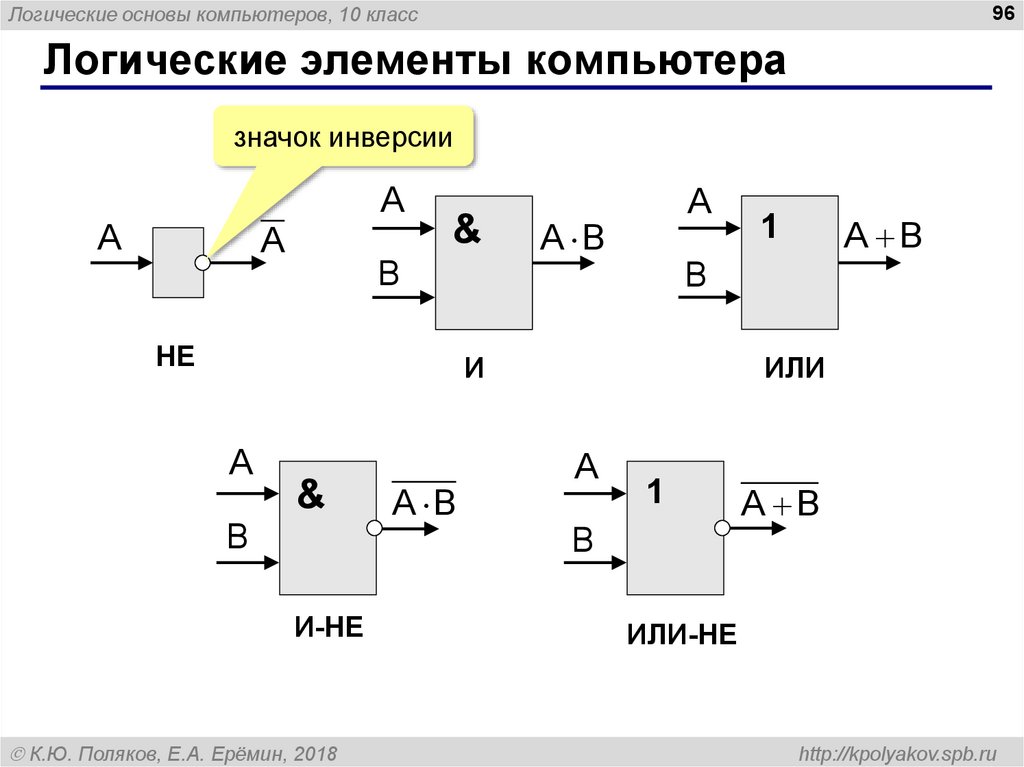
Логические элементы компьютера
значок инверсии
A
A
A
&
A
A B
B
НЕ
B
И
A
&
B
A B
A B
1
ИЛИ
A
1
A B
B
И-НЕ
К.Ю. Поляков, Е.А. Ерёмин, 2018
ИЛИ-НЕ
http://kpolyakov.spb.ru
95. Логические основы компьютеров
Логические основы компьютеров, 10 класс97
Логические элементы компьютера
Любое логическое выражение можно реализовать на
элементах И-НЕ или ИЛИ-НЕ.
И: A B A B
НЕ: A A A A A
A
&
A
A
ИЛИ:
B
A
&
& A B
A
A B A B
&
B
A B
&
A B
&
B
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
96. Логические элементы компьютера
Логические основы компьютеров, 10 класс98
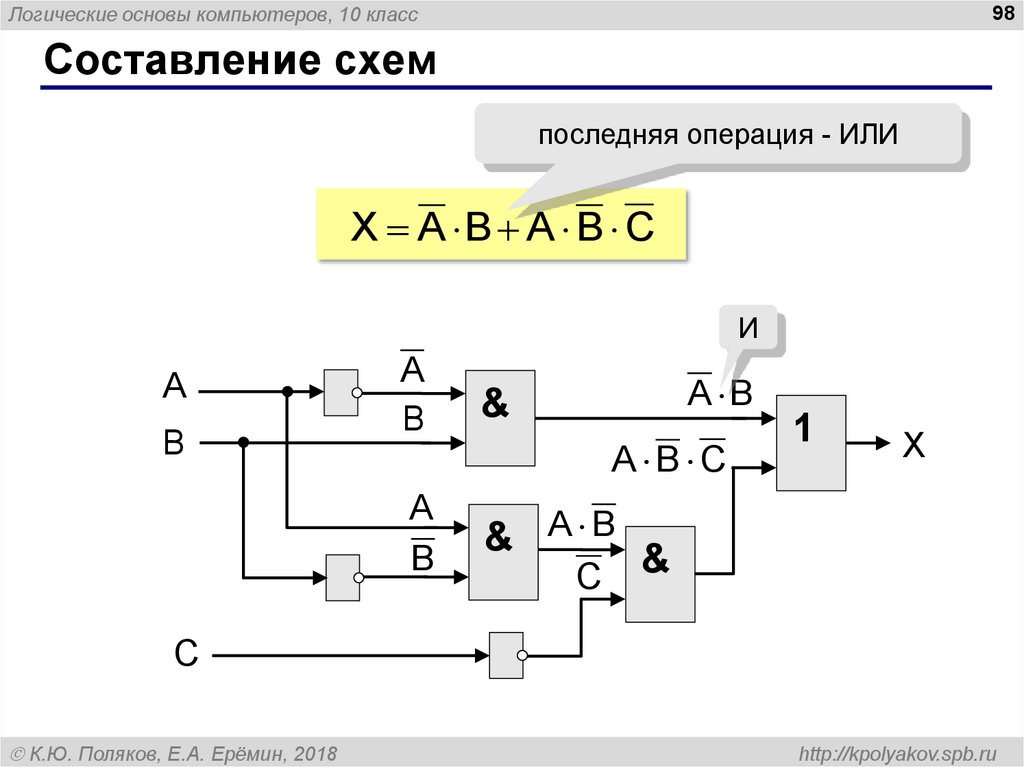
Составление схем
последняя операция - ИЛИ
X A B A B C
И
A
B
A
B
&
A
B
& A B
A B
A B C
C
1
X
&
C
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
97. Логические элементы компьютера
Логические основы компьютеров, 10 класс99
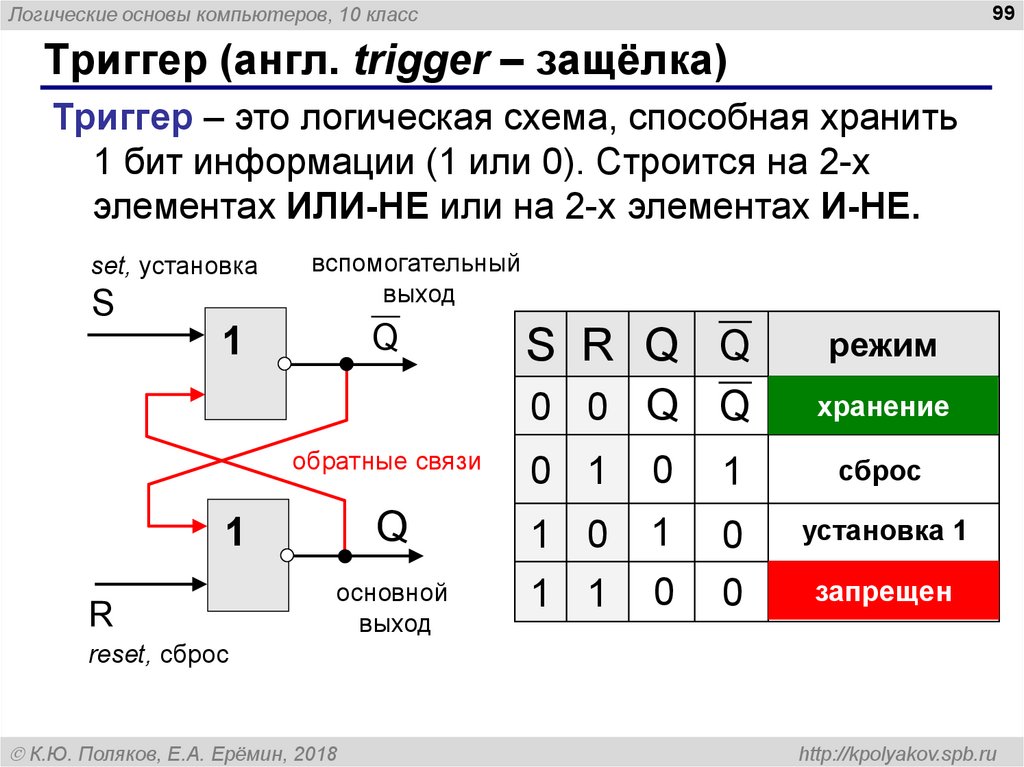
Триггер (англ. trigger – защёлка)
Триггер – это логическая схема, способная хранить
1 бит информации (1 или 0). Строится на 2-х
элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.
set, установка
S
вспомогательный
выход
Q
1
режим
0 0 Q Q
хранение
обратные связи
0 1
0
1
сброс
Q
1 0
1 1
1
0
0
0
установка 1
1
R
S R Q Q
основной
выход
запрещен
reset, сброс
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
98. Составление схем
Логические основы компьютеров, 10 класс100
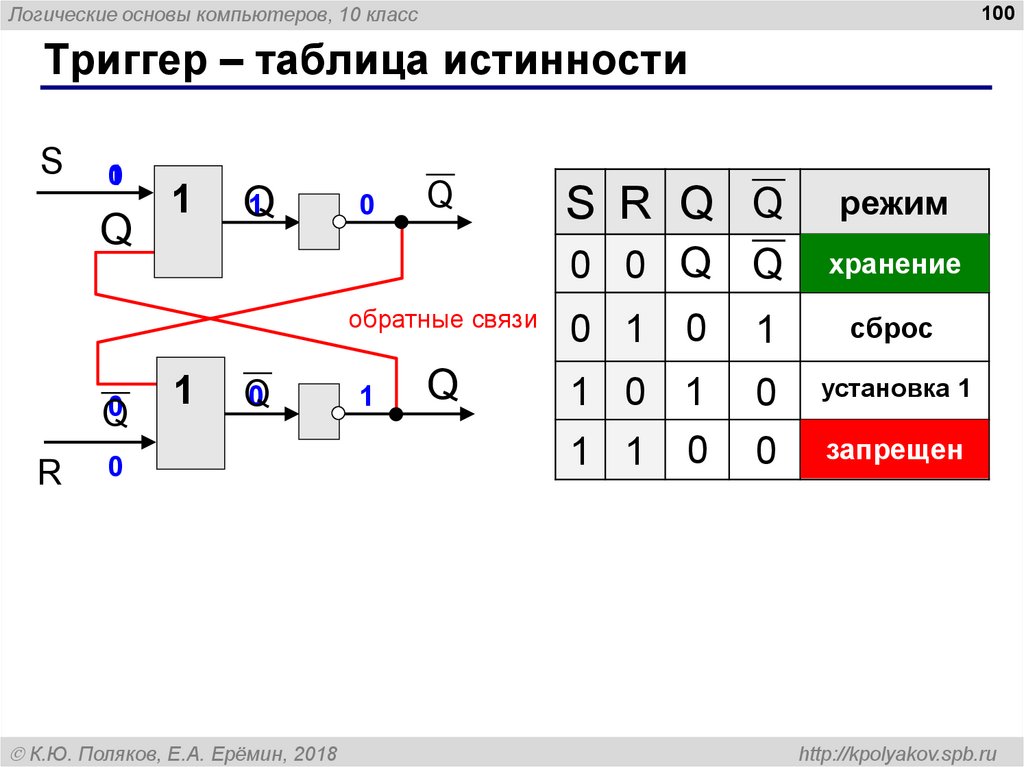
Триггер – таблица истинности
S
1
0
Q
0
Q
R
1
1
1
Q
0
Q
0
К.Ю. Поляков, Е.А. Ерёмин, 2018
0
Q
S R Q Q
режим
0 0 Q Q
хранение
обратные связи
0 1 0
1
сброс
Q
1 0 1
1 1 0
0
0
установка 1
1
запрещен
http://kpolyakov.spb.ru
99. Триггер (англ. trigger – защёлка)
Логические основы компьютеров, 10 класс101
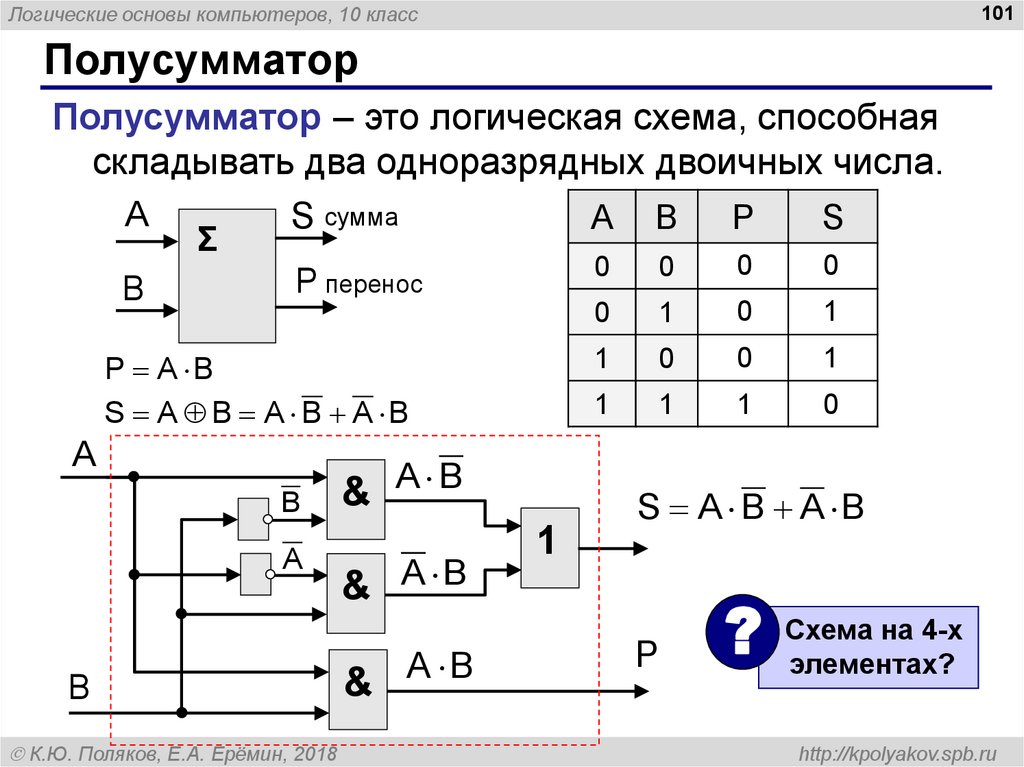
Полусумматор
Полусумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа.
A
S сумма
A B
P
S
Σ
B
P перенос
P A B
S A B A B A B
A
B
A
B
К.Ю. Поляков, Е.А. Ерёмин, 2018
& A B
& A B
& A B
1
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
S A B A B
P
на 4-х
? Схема
элементах?
http://kpolyakov.spb.ru
100. Триггер – таблица истинности
Логические основы компьютеров, 10 класс102
Сумматор
Сумматор – это логическая схема, способная
складывать два одноразрядных двоичных числа с
переносом из предыдущего разряда.
A
B
перенос C
Σ
A
B
C
P
S
0
0
0
0
0
S сумма
0
0
1
0
1
P перенос
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
101. Полусумматор
Логические основы компьютеров, 10 класс103
Многоразрядный сумматор
это логическая схема, способная складывать два
n-разрядных двоичных числа.
X
xn-1 xn-2 x0
110
Y
yn-1 yn-2 y0
011
Z p zn-1 zn-2 z0
1001
перенос
x0 0
y0 1
0
Σ
z0 1
x1 1
Σ
y1 1
p1 0
К.Ю. Поляков, Е.А. Ерёмин, 2018
z1 0
x2 1
Σ
y2 0
p2 1
z2 0
p 1
перенос
http://kpolyakov.spb.ru
102. Сумматор
Логические основы компьютеров, 10 класс104
Конец фильма
ПОЛЯКОВ Константин Юрьевич
д.т.н., учитель информатики
ГБОУ СОШ № 163, г. Санкт-Петербург
kpolyakov@mail.ru
ЕРЕМИН Евгений Александрович
к.ф.-м.н., доцент кафедры мультимедийной
дидактики и ИТО ПГГПУ, г. Пермь
eremin@pspu.ac.ru
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru
103. Многоразрядный сумматор
Логические основы компьютеров, 10 класс105
Источники иллюстраций
1.
2.
3.
http://www.peoples.ru
http://ru.wikipedia.org
авторские материалы
К.Ю. Поляков, Е.А. Ерёмин, 2018
http://kpolyakov.spb.ru












































































 informatics
informatics








