Квадратичная функция

1.

Квадратичная функция.

2.

Квадратичной функцией называется функция,
которую можно задать формулой вида
y = ax² + bx + c, где
х – независимая переменная, a, b и с – некоторые
числа (причём а ≠ 0).
Например:
у = 5х² + 6х + 3
у = –7х² + 8х – 2,
у = 0,8х² + 5,
у = ¾х² – 8х,
у = –12х²
квадратичные функции.

3.

Перемещение х тела при движении с
ускорением а описывается квадратичной
функцией
где хо и V0 - положение и скорость
тела в начальный момент времени
t = 0.

4.

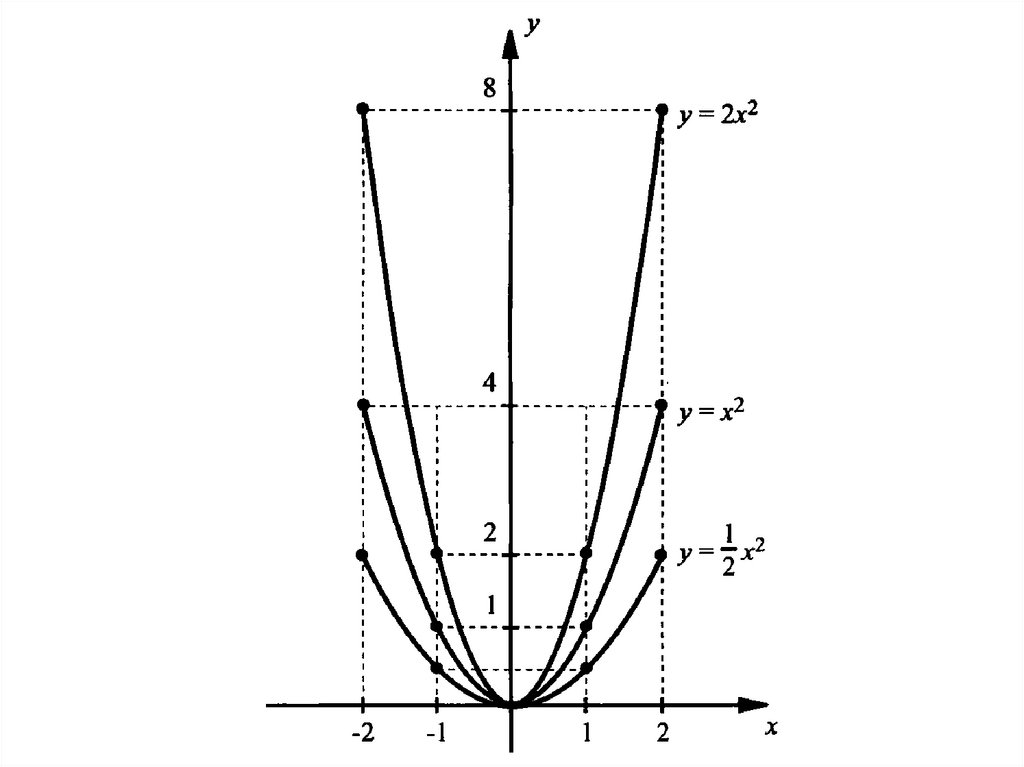
Пример 1. Составить таблицу значений и в одной
системе координат построить графики функций
–2
–1,5
–1
–0,5
0
0,5
1
1,5
2
При каждом значении х значения функции у = 1/2х2 в два раза
меньше значений функции у = х2, а значения функции у = 2х2
в два раза больше значений функции у = х2. Другими словами,
график функции у = 1/2х2 можно получить сжатием в два
раза вдоль оси ординат графика функции у = х2. График
функции у = 2х2 можно получить растяжением в два раза
вдоль оси ординат графика функции у = х2.

5.

6.

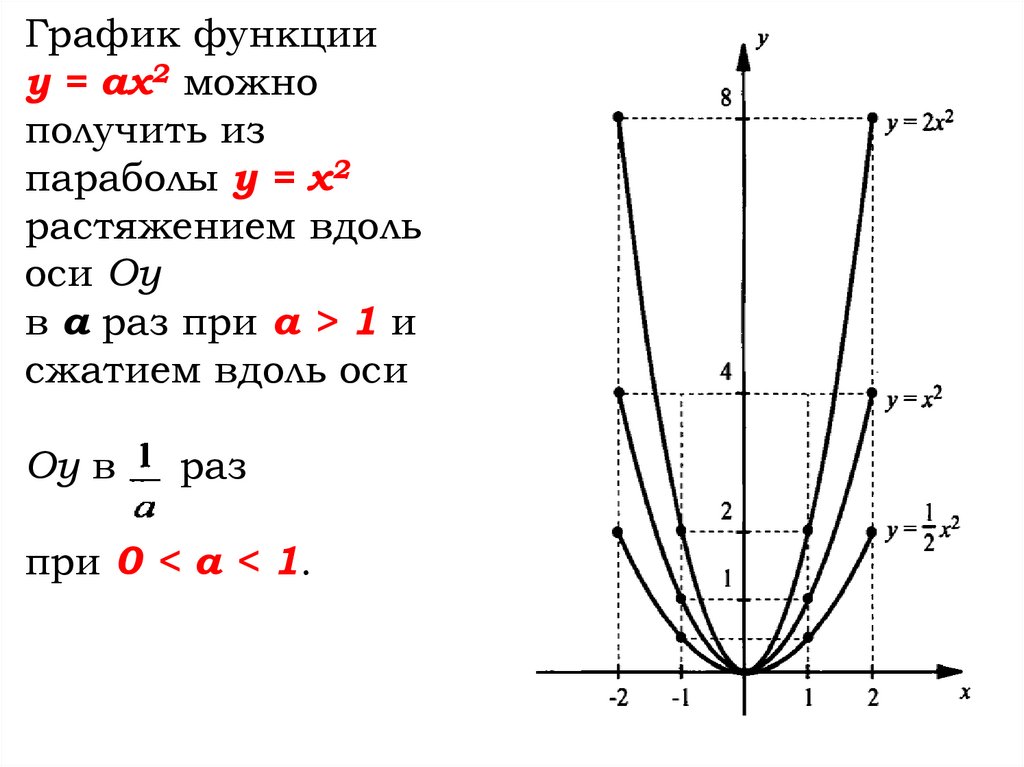
График функции
у = ах2 можно
получить из
параболы у = х2
растяжением вдоль
оси Оу
в а раз при а > 1 и
сжатием вдоль оси
Оу в
раз
при 0 < a < 1.

7.

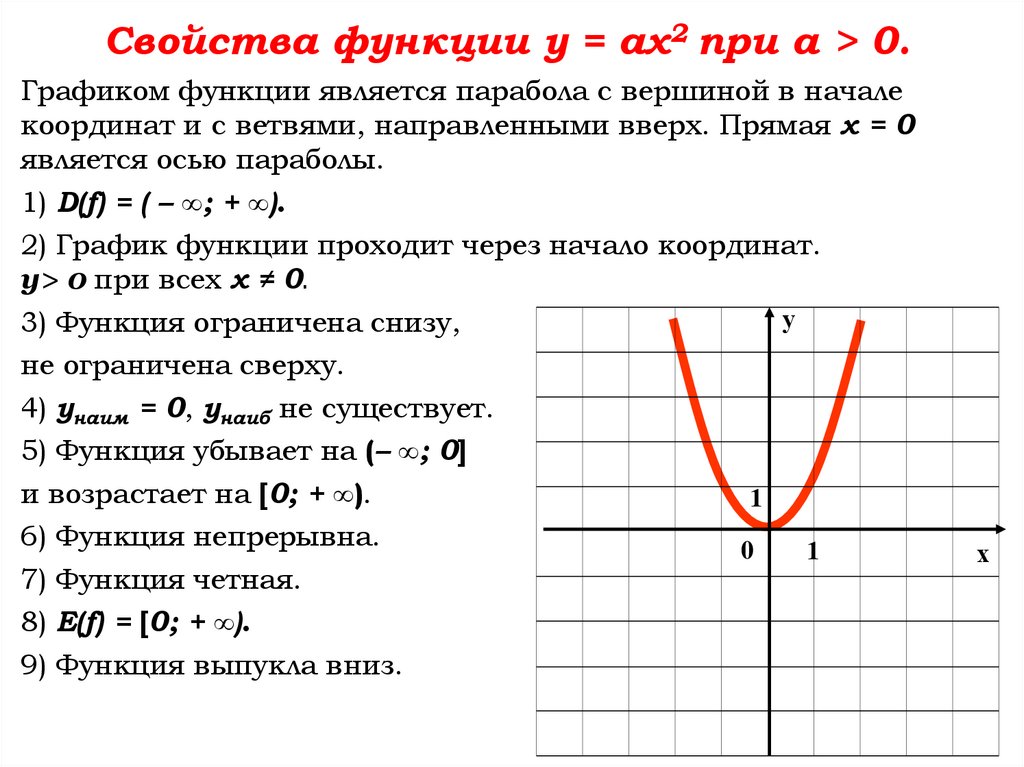
Свойства функции у = ах2 при а > 0.
Графиком функции является парабола с вершиной в начале
координат и с ветвями, направленными вверх. Прямая х = 0
является осью параболы.
1) D(f) = ( – ∞; + ∞).
2) График функции проходит через начало координат.
y> 0 при всех х ≠ 0.
у
3) Функция ограничена снизу,
не ограничена сверху.
4) унаим = 0, унаиб не существует.
5) Функция убывает на (– ∞; 0]
и возрастает на [0; + ∞).
1
6) Функция непрерывна.
0
1
7) Функция четная.
8) E(f) = [0; + ∞).
9) Функция выпукла вниз.
х

8.

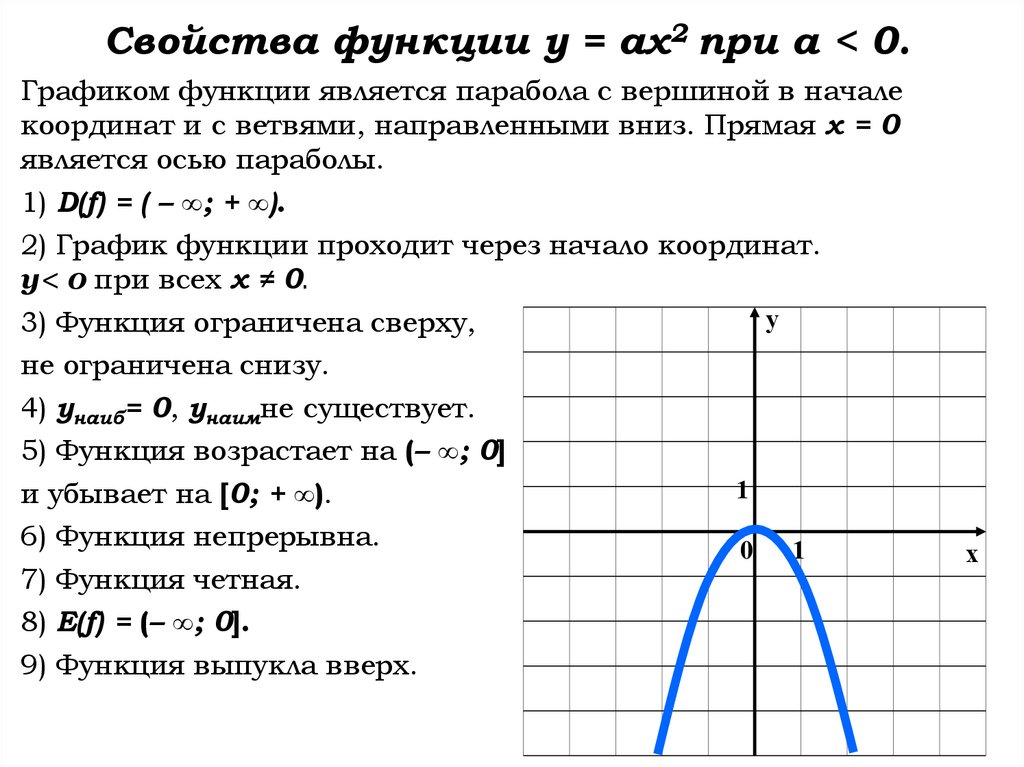
Свойства функции у = ах2 при а < 0.
Графиком функции является парабола с вершиной в начале
координат и с ветвями, направленными вниз. Прямая х = 0
является осью параболы.
1) D(f) = ( – ∞; + ∞).
2) График функции проходит через начало координат.
у< 0 при всех х ≠ 0.
у
3) Функция ограничена сверху,
не ограничена снизу.
4) унаиб= 0, унаимне существует.
5) Функция возрастает на (– ∞; 0]
1
и убывает на [0; + ∞).
6) Функция непрерывна.
1
0
7) Функция четная.
8) E(f) = (– ∞; 0].
9) Функция выпукла вверх.
х