Квадратичная функция

1.

2.

Квадратичной функцией называется
функция, заданная формулой
у = ах2 + bх + с,
а 0.

3.

1) у = х2
У
9
4
1
О
1 23
Х
Свойства функции:
1) область определения: Х = R
2) множество значений: У = 0;+
3) f(-х) = (-х)2 = х2 = f (х)
функция четная,
4) график - парабола,
ветви вверх,
вершина О(0; 0)
ось симметрии – Оу
5) возрастает на 0; + ,
убывает на - ; 0 .

4.

2) у = ах2
а>0
у = 2х2
у = х2
у = 0,5х2
у
О
Свойства функции:
1) область определения: Х = R
2) множество значений: У = 0;+
3) f(-х) = а(-х)2 = ах2 = f (х)
функция четная,
4) график - парабола,
вершина О(0; 0),
ветви вверх,
хось симметрии – Оу
5) возрастает на 0; + ,
убывает на - ; 0 .

5.

а<0
Свойства функции:
у
х
у =- 2х2
у =- х2
у =- 0,5х2
О
Самостоятельно
аналогично.

6.

3) у = ах2 + n
Свойства функции:
а>0
1) Область определения: Х = R
2) Множество значений: У= n; +
3) f(-х) = а(-х)2 + n = ах2 + n = f (х)
функция четная,
4) график - парабола,
ветви вверх,
вершина (0; n),
ось симметрии параболы - Оу
5) возрастает на 0; + ,
убывает на - ; 0 .
у=2х2
у=2х2+1
у=2х2-1
у
1
О
-1
х

7.

Свойства функции:
а<0
Самостоятельно аналогично

8.

4) у = а(х - m)2
Свойства функции:
а>0
1) Область определения: Х = R
2) Множество значений: У= 0; +
3) f(-х) = а((-х-m)2 f (х) -f(х)
функция ни четная, ни нечетная
4) графиком функции является
парабола,
ветви вверх,
вершина (m; 0),
ось симметрии – прямая х = m
5) возрастает на m; + ,
убывает на - ; m .
у=2х2
у=2(х+1)2
у=2(х-1)2
у
-1 О
1
х

9.

Свойства функции:
а<0
Самостоятельно аналогично

10.

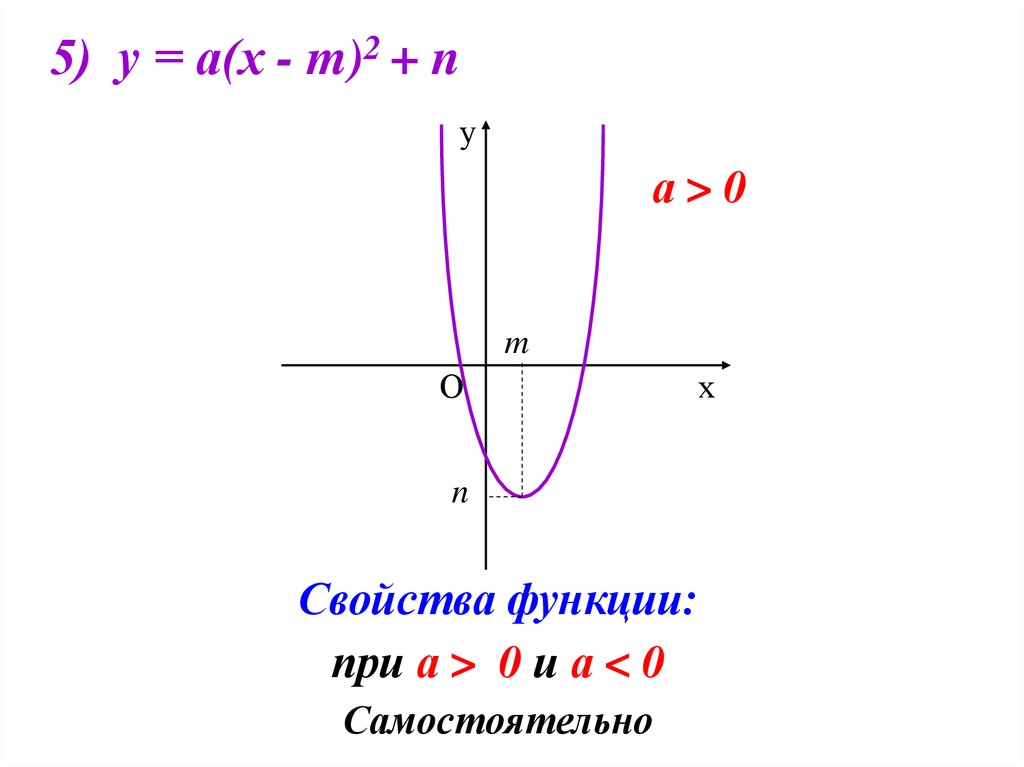
5) у = а(х - m)2 + n
у
а>0
m
О
n
Свойства функции:
при а > 0 и а < 0
Самостоятельно
х

11.

Построение графика функции
у = ах2 + bх + с
1 способ
1) из квадратного трехчлена ах2 + bх + с выделить
полный квадрат: у = а(х – m)2 + n:
ах2
+ bх + с =
а(х2
b
b
с
b
2
+ a х + ) = а(х + 2·х·
+
а
2a
2a
2
2
2
2
2
b
b
4
ac
b
b
4ac
b с
a x
- + ) = а х
2
a
2a
4a
4a
2a а
2
b
Обозначим 2a
b 2 4ac
= m, = n.
4a
Получим у = ах2 + bх + с = а(х – m)2 + n.

12.

2) определить координаты вершины параболы – (m; n)
3) построить вспомогательный график функции у = ах2
4) выполнить перемещения вспомогательного графика
в направлениях параллельных координатным осям:
а) параллельно оси Ох:
на m единиц вправо, если m > 0,
на |m| единиц влево, если m < 0;
б) параллельно оси Оу:
на n единиц вверх, если n > 0,
на |n| единиц вниз, если n < 0.

13.

2 способ
1) Найти координаты вершины параболы:
абсцисса х0 b , ордината у0 = у(х0)
2а
2) Найти (если возможно) абсциссы точек
пересечения параболы с осью Ох:
это корни уравнения ах2 + bх + с = 0.
3) Найти ординату точки пересечения параболы с
осью Оу: это у = у(0) = с.
4) Найти абсциссу точки, симметричной точке (0; с)
относительно оси симметрии параболы:
это корень уравнения ах2 + bх + с = с.
5) Можно построить еще несколько точек искомого
графика, выбрав несколько значений х и подсчитав
соответствующие им значения у.

14.

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
Дробно-линейной функцией называется функция
ax b
у=
,
cx d
полученная при делении друг на друга двух
линейных функций.
ax b a
b
линейная
x
1) с = 0, d 0 у =
функция
d
d
d
b к
b
(где k = ) –
2) а = d = 0, с 0 у =
с
сх х
обратная пропорциональность

15.

3) с 0, d 0, аd = bс а b = р а = ср, b = dр
с
d
ср х dр р(сх d )
у=
=рcx d
cx d )
постоянная функция
4х 6
Пример. Построить график функции у =
2х 5
у=
3
3 5 5
4 х 2 х
2
2 2 2
5
5
2 х
х
2
2
График функции у =
2
графика функции у = х
на 2 единицы вверх.
2
5
5
2 х 1 2 х 2
2
2
2
2
5
5
5
х
х
х
2
2
2
2
5
х
2
получается сдвигом
на 5/2 единицы влево и

16.

у = 2
у
2
х
5
2
2
-5/2
О
х
2
у=х

17.

ОБРАТНАЯ ФУНКЦИЯ
б)
у
d
у0
а)
с
у
d
у0
О
с
О
а
х0
b
х
а х1 х2
х3
b
х

18.

у
у = f(х)
d
у0
с
О
а
х0
b
х
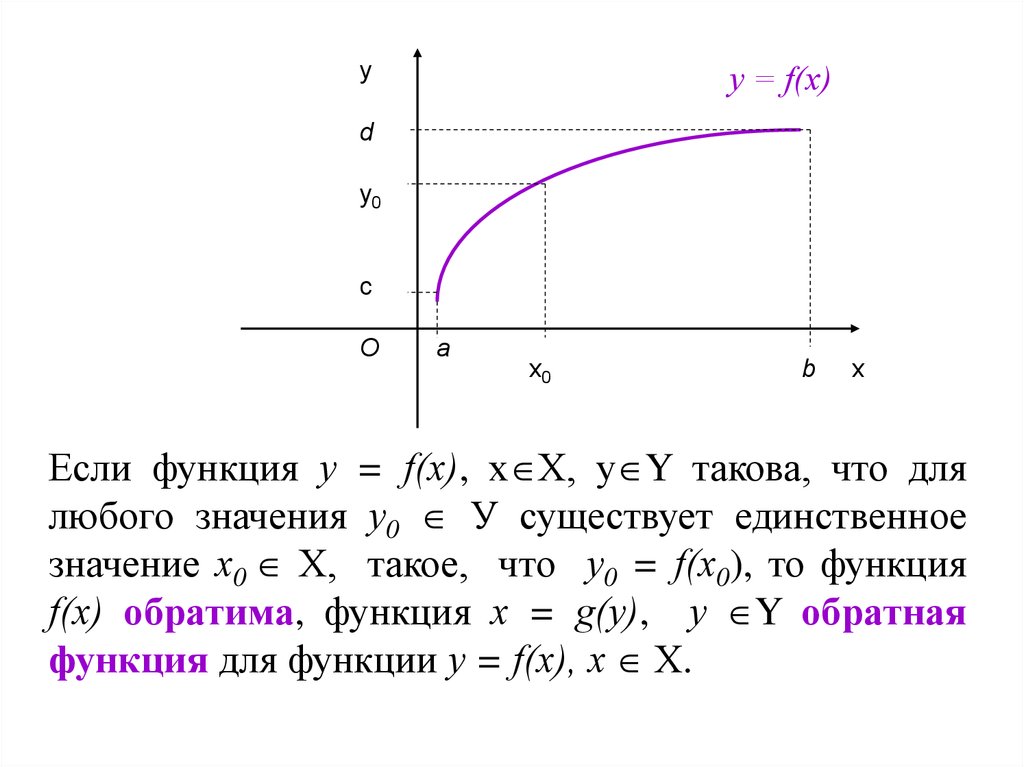
Если функция у = f(х), х Х, у Y такова, что для
любого значения у0 У существует единственное
значение х0 Х, такое, что у0 = f(х0), то функция
f(х) обратима, функция х = g(у), у Y обратная
функция для функции у = f(х), х Х.

19.

Чтобы найти выражение для обратной функции,
надо решить уравнение у = f(х) относительно х, беря
лишь те решения, которые принадлежат множеству Х,
и поменять местами х и у.
Если функция у = f(х) определена и возрастает
(убывает) на промежутке Х, и областью ее значений
является промежуток Y, то у нее существует обратная
функция, которая определена и возрастает (убывает)
на Y.

20.

Графики взаимно обратных функций симметричны
относительно прямой у = х (биссектрисы 1-й и 3-й
координатных четвертей)
У
у=х
у=f(х)
О
Х

21.

Примеры:
1) Для функции у = 2х – 1 найти обратную функцию.
Построить графики обеих функций.
Функция возрастает на
всей числовой прямой,
значит, у нее есть
обратная функция
у 1
х=
2
х 1
у=
2
1
1
или у = х
2
2
У
у=2х – 1
у=х
у
1
1
1
х
=2 2
-1
О
1
-1
х

22.

2) у = х2, х R
Эта функция не имеет обратной функции, так как, одно и
то же значение у может соответствовать разным
значениям х: 32 = (-3)2 = 9.
у
у = х2
3) у = х2, х R+
Функция возрастает на
всей области
определения, значит, у
нее есть обратная
функция
х= у
у= х
у=х
у
=
х
О
х

23.

КОМПОЗИЦИЯ ФУНКЦИЙ
у = f(х), х Х и х = g(t), t Т, х Х
t х = g(t) у = f(х),
f(g(t))
Сложная функция у = f(g(t)) называется
композицией функций у = f(х), х Х и
х = g(t), t Т.
От лат. соmроsitiо – составление

24.

Примеры: 1) у = х2 + 1 и х = 3t – 4,
у(х(t))= (3t – 4)2 + 1.
2) f(х) = х2 - 2х, g(х) = 4х +3
f(g(х)) = (4х + 3)2 – 2(4х + 3), g(f(х)) = 4(х2 – 2х) + 3
3) f(х) =
х , х 0 композиция функций у = f[g(t)]
g(t) = - t2 – 1
g 0
у = g [f (х)] = - х -1
не определена