Первое начало термодинамики

1. Первое начало термодинамики

2. Первое начало термодинамики

•Первое
начало
термодинамики
–
это
количественное выражение закона сохранения и
превращения энергии.
•Исходное выражение первого начала термодинамики
по
внешнему
балансу
теплоты
и
работы
формулируется
следующим
образом:
количество
теплоты, подведенное к системе извне
Q1,2 , идет на изменение ее внутренней энергии
( U1,2 U 2 U1 ) и на выполнение системой внешней
L 1,2
работы
*
Q1,2 U 2 U1 L 1,2
•и в дифференциальной форме
Q dU L
*

3.

Математические
выражения
первого
начала
термодинамики по внешнему балансу теплоты и
работы.
Уравнение первого начала термодинамики по
балансу рабочего тела
Q Q Q dU L
Математическое
выражение
первого
начала
термодинамики по балансу рабочего тела в
дифференциальной форме для простых тел
•для термодинамической системы
Q dU L dU pdV
•для 1 кг системы
q du l du pdv

4.

w vdp pdv pdv pdv d ( pv )
w l d ( pv )
l w d ( pv )
Первое начало термодинамики для открытых
термодинамических
систем,
являющихся
простым телом
q du w d ( pv )
q d ( u pv ) w
u
Сумма удельной внутренней энергии
и удельной
потенциальной функции pv , находящихся под знаком
полного
дифференциала,
называется
удельной
энтальпией
h u pv
Полная энтальпия
H h G.

5.

•Удельную потенциальную функцию системы
pv можно представить как потенциальную
энергию, равную работе, затраченной для
повышения давления 1 кг простого тела в
процессе (0-1) от нулевого уровня ( p0 0
,
вакуум) до давления p1 p .
•Следовательно, энтальпия представляет из
себя сумму внутренней энергии системы и
ее
потенциальной
энергии,
значение
которой
определяется
избыточным
давлением системы.
•Пусть h f ( p , T ) ,
с
учетом
одного
из
дифференциальных соотношений термодинамики
h p T
1
p T T h h p

6.

получаем
h
h
h T
dp c p dT (c p Dh )dp
dh
dT dp c p dT
T p
T p p h
p T
где Dh
T
.
– коэффициент Джоуля-Томсона, Dh
p h
С учетом уравнения распределения потенциальной работы
2
c
**
w wвн d g dz w
2
получаем математического выражения первого начала
термодинамики для потока простого тела (жидкости или
газа):
2
c
*
**
q q q dh w c p dT ( c p Dh )dp wвн d g dz w**
2

7.

• Первое начало термодинамики для открытой
термодинамической системы, состоящей из
1 кг простого тела, по балансу рабочего тела
в дифференциальной и интегральной формах
q q q dh vdp dh w
*
**
2
q1, 2 q1, 2 q1, 2 h2 h1 vdp h1, 2 w1, 2
*
1
• Математическое выражение первого начала
термодинамики
для
открытой
термодинамической системы по внешнему
балансу в дифференциальной и интегральной
форме
*
*
q dh w
q1*, 2 h2 h1 w1*, 2

8.

Первое начало термодинамики в
аналитической форме
Для простого тела, если
u f ( T ,v ) , а h f ( T , p )
u
u
u
du
dT dv cv dT dv
T v
v T
v T
h
h
h
dh
dT dp c p dT dp
T p
p T
p T
математическое
выражение
первого
термодинамики принимает следующий вид:
начала
h
u
q cv dT dv pdv c p dT dp vdp
v T
dp T

9.

а с учетом дифференциальных соотношений
термодинамики
u v T
1
v T T u u v
h p T
1
p T T h h p
получаем выражение первого начала термодинамики в
аналитической форме
q cv dT ( cv Du ) dv pdv c p dT ( c p Dh ) dp vdp
где Du – коэффициент Джоуля – Гей Люссака, Du T
T
v u
–
коэффициент
Джоуля-Томсона,
Dh
Dh
p h
которые для реальных газов определяются по
таблицам
термодинамических
свойств,
представленным в справочной литературе.

10. Примеры использования I начала термодинамики для потока

Вывод уравнения В.Г. ШУХОВА
Q dH W
W 0
Q k Dн ( tпг tгр ) dx
dH G c p dt
k Dн ( tпг tгр ) dx G c p dt
Разделив переменные и проинтегрировав, получаем
t x tгр ( t1 tгр ) exp( ax / L )
где
а - параметр В.Г. Шухова
a km Dн L /( G c pm )

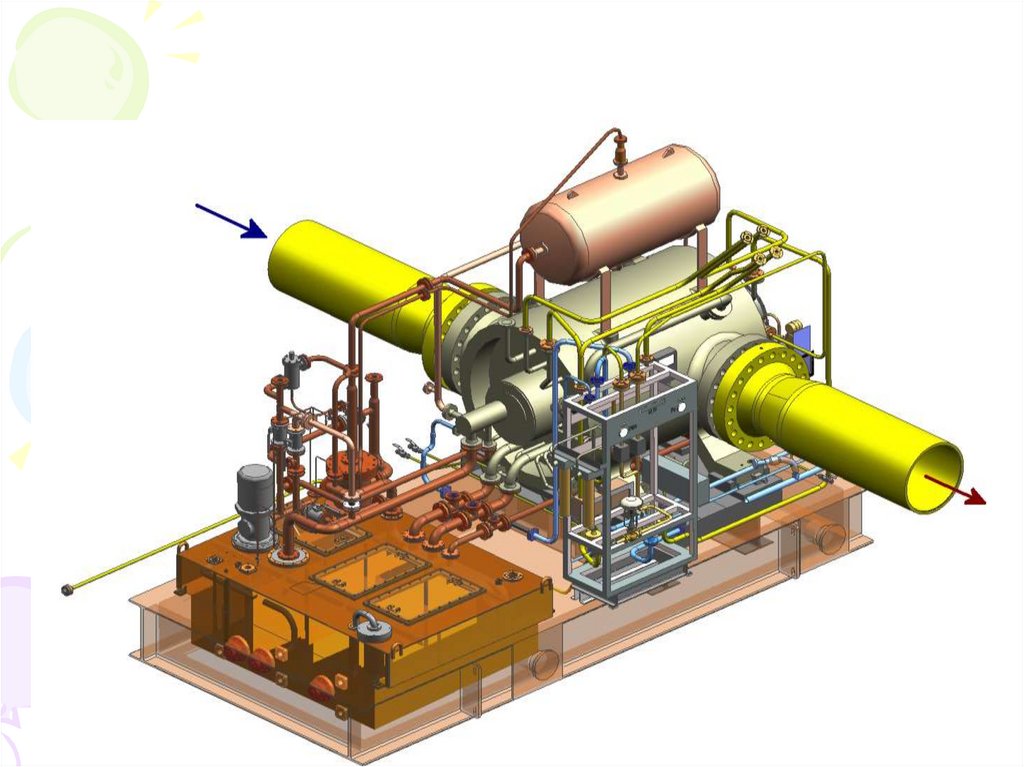
11. Работа и мощность сжатия в системе компримирования КС

q1,2 0
*
*
q1, 2 h2 h1 w1, 2
*
w1,2 h1,2
N сж Ni G w1,2 G h1,2
пол
w1,2
w1,2
w1,2
h1,2

12.

p
p1
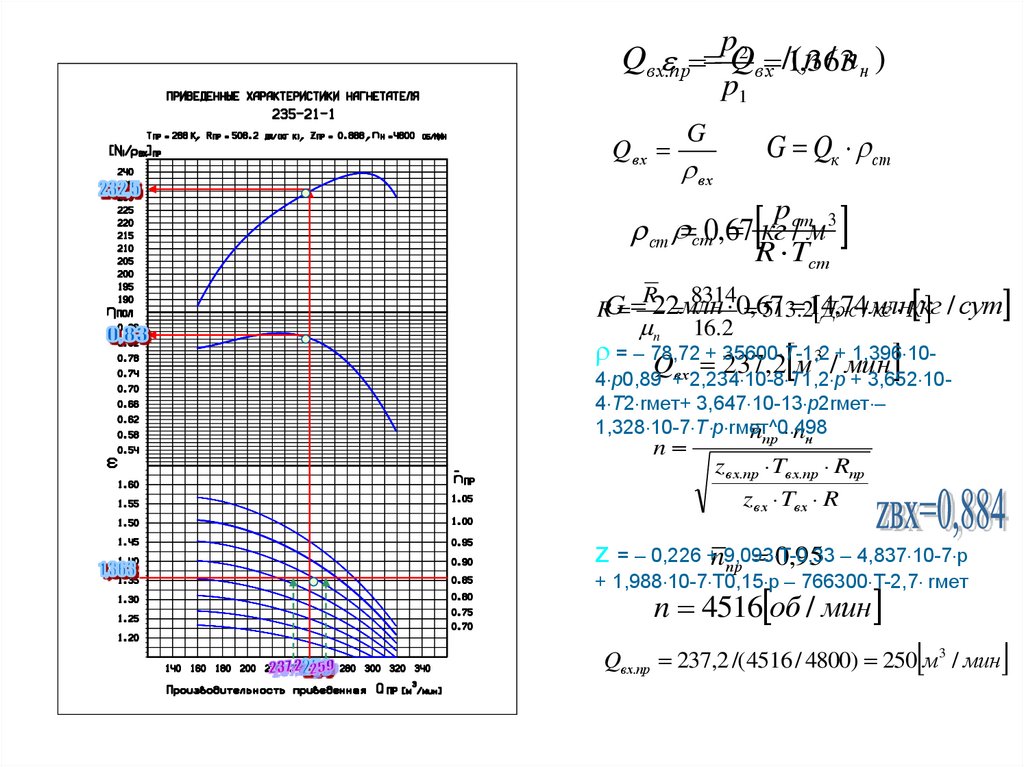
Qв х .пр Q2 в х /(1,n363
/ nн )
Qв х
G Qк ст
G
вх
pст 3
кг / м
ст ст0,67
R Tст
R 8314
,74/млн
Дж
/ сут
RG 22 млн 0 ,67
513 .214
кг Ккг
n 16.2
= – 78,72
35600 T-1,2
1,396 10
Q + 237
,2 м 3 /+мин
в х2,234 10-8 T1,2 p + 3,652 104 p0,89 +
4 T2 rмет+ 3,647 10-13 p2rмет –
1,328 10-7 T p rмет^0.498
nпр nн
n
zв х.пр Tв х.пр Rпр
zв х Tв х R
z = – 0,226 +n9,093 T-0,33
– 4,837 10-7 p
пр 0,95
+ 1,988 10-7 T0,15 p – 766300 T-2,7 rмет
n 4516 об / мин
Qвх.пр 237,2 /( 4516 / 4800) 250 м 3 / мин

13. Первое начало термодинамики для идеальных газов. Закон Майера. Энтропия идеального газа

pv RT
•Согласно уравнению Клапейрона
и закону Джоуля u u( T )
h u pv h( T )
, du c dT ,
v
u2 u1 cvm T2 T1
,
dh c p dT
,
h2 h1 c pm ( T2 T1 )

14.

•Уравнение первого начала термодинамики для
идеального газа по балансу рабочего тела в
дифференциальной и интегральной формах:
q q q cv dT pdv c p dT vdp
q1,2 cvm T2 T1 l1,2 c pm T2 T1 w1,2
•Закон Майера
( c p cv ) dT pdv vdp d ( pv ) RdT
c p cv R
c p cv ( c p cv ) R R

15.

•Энтропия идеального газа
q
dT p
dT v
cv
dv c p
dp
T
T T
T T
Так как:
p R
T v
,
v R
T p
получаем
q
dT
dv
dT
dp
cv ( T )
R cp( T )
R
T
T
v
T
p
Правая часть уравнения представляет собой сумму
полных дифференциалов. Это значит, что и соотношение q / T есть полный дифференциал
некоторой функции состояния идеального газа (s),
называемой удельной энтропией.
q q* q**
ds
T
T

16.

•Изменение удельной энтропии идеального газа в
процессе (1-2)
T2
v2
T2
p1
s2 s1 cmv ln R ln cmp ln R ln
T1
v1
T1
p2
где c mp , cmv
теплоемкости
- вторые средние удельные
2
1
cmz
cz d ln T
ln T2 ln T1 1
при
c z a z bz T
2
dT
a z bzT T
T2 T1
1
cmz
a z bz
a z bz Tmz
T2
T2
ln
ln
T1
T1