Глава III Многогранники Решение задач

1.

Глава III Многогранники
Решение задач

2.

Площадь боковой поверхности призмы
Площадь боковой поверхности призмы равна
сумме площадей всех ее боковых граней

3.

Площадь полной поверхности призмы
Площадь полной поверхности призмы равна
сумме площадей всех ее боковых граней и
оснований

4.

Пример
Прямая треугольная призма
Состоит из 2 треугольников и 3 прямоугольников
Тогда, площадь боковой поверхности равна
сумме площадей трех прямоугольников, а
площадь полной поверхности равна сумме
площадей
двух
треугольников
и
трех
прямоугольников

5.

Задача №1
Найдите площадь боковой поверхности
правильной шестиугольной призмы,
сторона основания которой равна 5, а
высота — 10

6.

Задача №1. Решение
Площадь боковой поверхности призмы равна
сумме площадей всех ее боковых граней:

7.

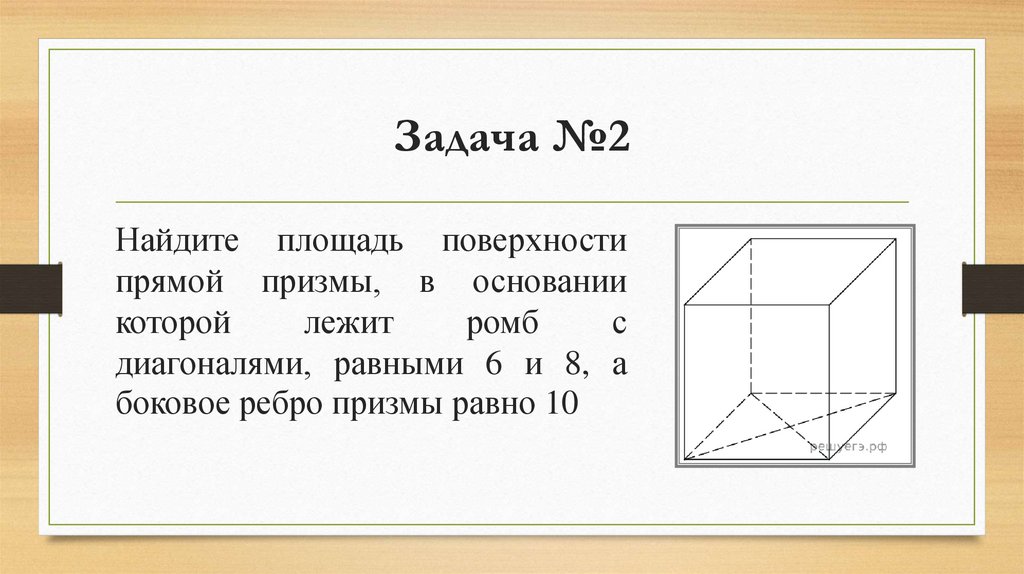
Задача №2
Найдите площадь поверхности
прямой призмы, в основании
которой
лежит
ромб
с
диагоналями, равными 6 и 8, а
боковое ребро призмы равно 10

8.

Задача №2. Решение
По Т. Пифагора находим сторону ромба
(либо через Египетский треугольник),
сторона равна 5
?
4
3

9.

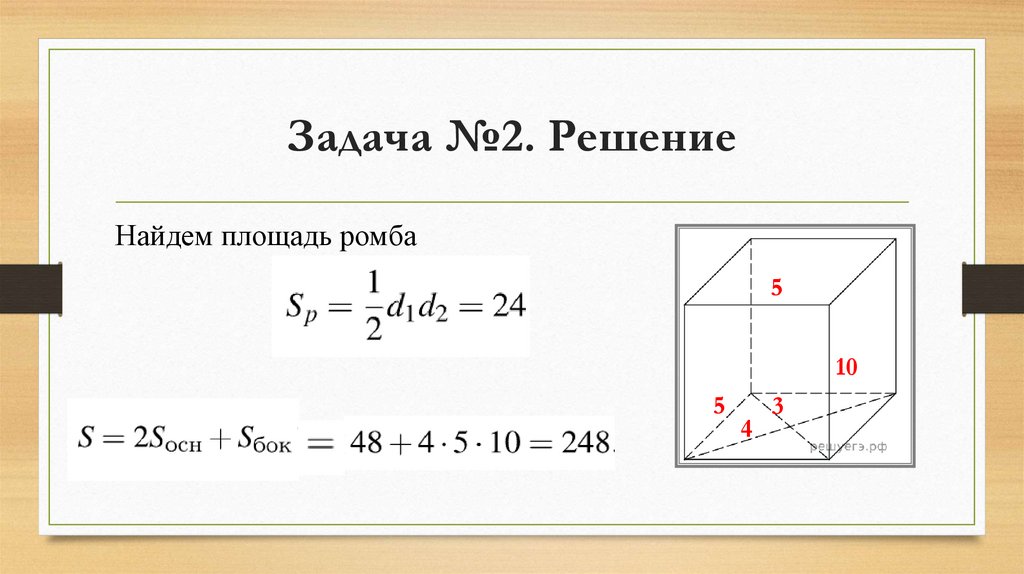
Задача №2. Решение
Найдем площадь ромба
5
10
5
4
3

10.

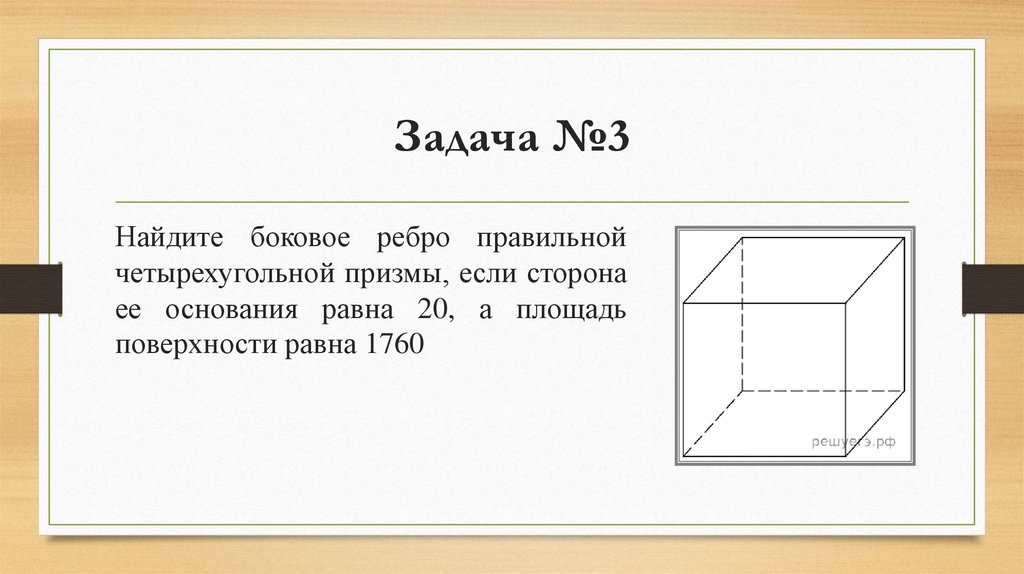
Задача №3
Найдите боковое ребро правильной
четырехугольной призмы, если сторона
ее основания равна 20, а площадь
поверхности равна 1760

11.

Задача №3. Решение
Правильная
четырехугольная
призма
состоит
из
6
четырехугольников: 2 квадрата
(основания) и 4 прямоугольника
(боковые грани)

12.

Задача №3. Решение
Площадь поверхности правильной
четырехугольной призмы выражается
через сторону ее основания a и боковое
ребро H формулой:

13.

Задача №3. Решение

14.

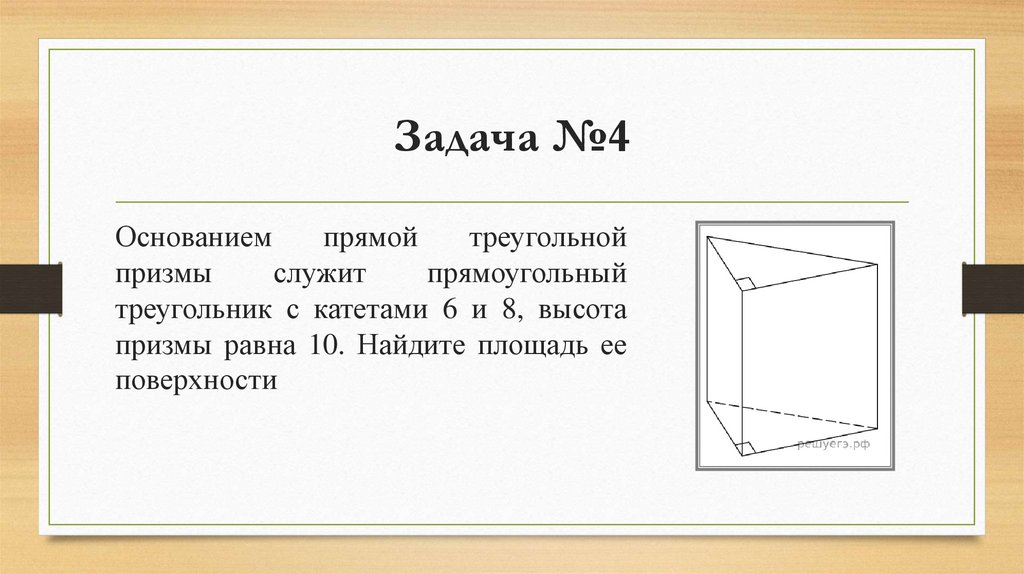
Задача №4
Основанием
прямой
треугольной
призмы
служит
прямоугольный
треугольник с катетами 6 и 8, высота
призмы равна 10. Найдите площадь ее
поверхности

15.

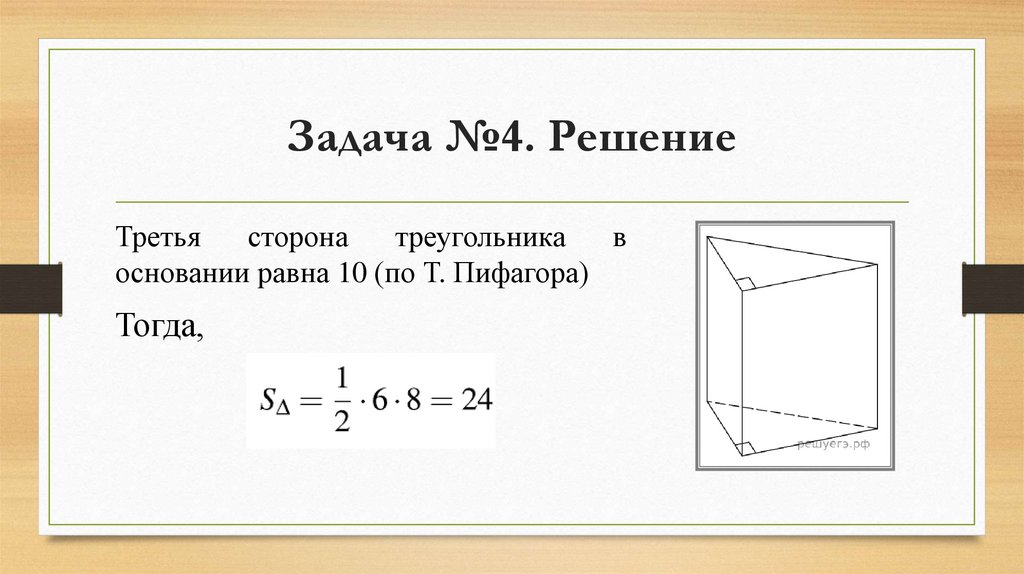
Задача №4. Решение
Третья
сторона
треугольника
в
основании равна 10 (по Т. Пифагора)
Тогда,

16.

Задача №4. Решение
Площадь боковой поверхности призмы