Similar presentations:
Правильные многогранники. Решение задач
1. Правильные многогранники. Решение задач.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ.РЕШЕНИЕ ЗАДАЧ.
Геометрия 10 класс
Яроцкая Л.П.
учитель математики СОШ № 38
Иркутск
2.
ПРАВИЛЬНЫЙ МНОГОГРАННИКвыпуклый многогранник, грани которого являются правильнымимногоугольниками с одним и тем же числом сторон
и в каждой вершине которого сходится одно и то же число ребер.
Тетраэдр
Икосаэдр
Октаэдр
Гексаэдр
Додекаэдр
3.
ТЕТРАЭДРТетраэдр – представитель правильных
выпуклых многогранников.
Поверхность тетраэдра состоит из
четырех равносторонних треугольников,
сходящихся в каждой вершине по три.
4.
КУБ (ГЕКСАЭДР)Куб или гексаэдр – представитель
правильных выпуклых
многогранников.
Куб имеет шесть квадратных граней,
сходящихся в каждой вершине по
три.
5.
ОКТАЭДРОктаэдр – представитель семейства
правильных выпуклых
многогранников.
Октаэдр имеет восемь треугольных
граней, сходящихся в каждой вершине
по четыре.
6.
ДОДЕКАЭДРДодекаэдр – представитель
семейства правильных выпуклых
многогранников.
Додекаэдр имеет двенадцать
пятиугольных граней, сходящихся в
вершинах по три.
7.
ИКОСАЭДРИкосаэдр – представитель семейства
правильных выпуклых
многогранников.
Поверхность икосаэдра состоит из
двадцати равносторонних
треугольников, сходящихся в каждой
вершине по пять.
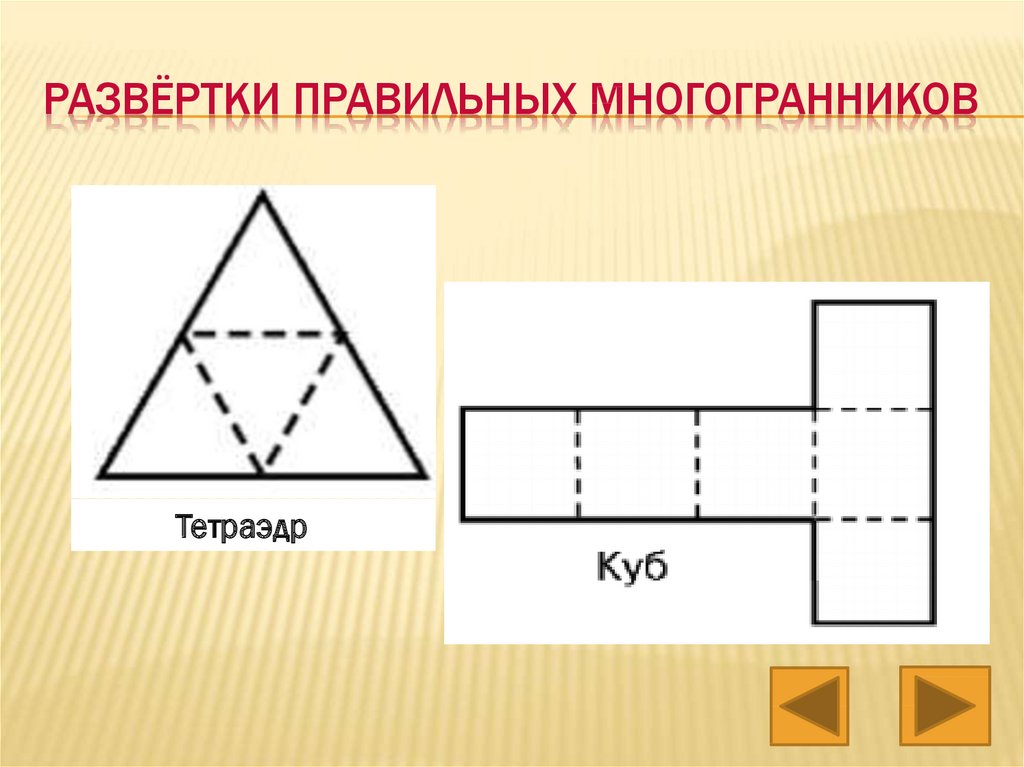
8. Развёртки правильных многогранников
РАЗВЁРТКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВТетраэдр
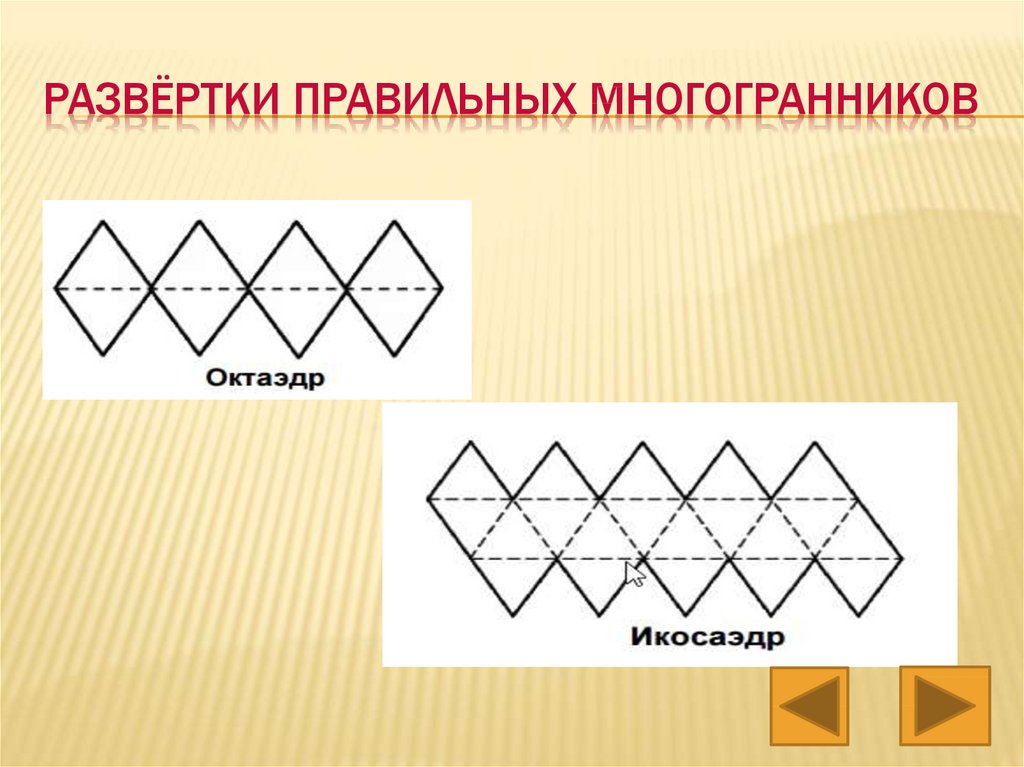
9. Развёртки правильных многогранников
РАЗВЁРТКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ10. Развёртки правильных многогранников
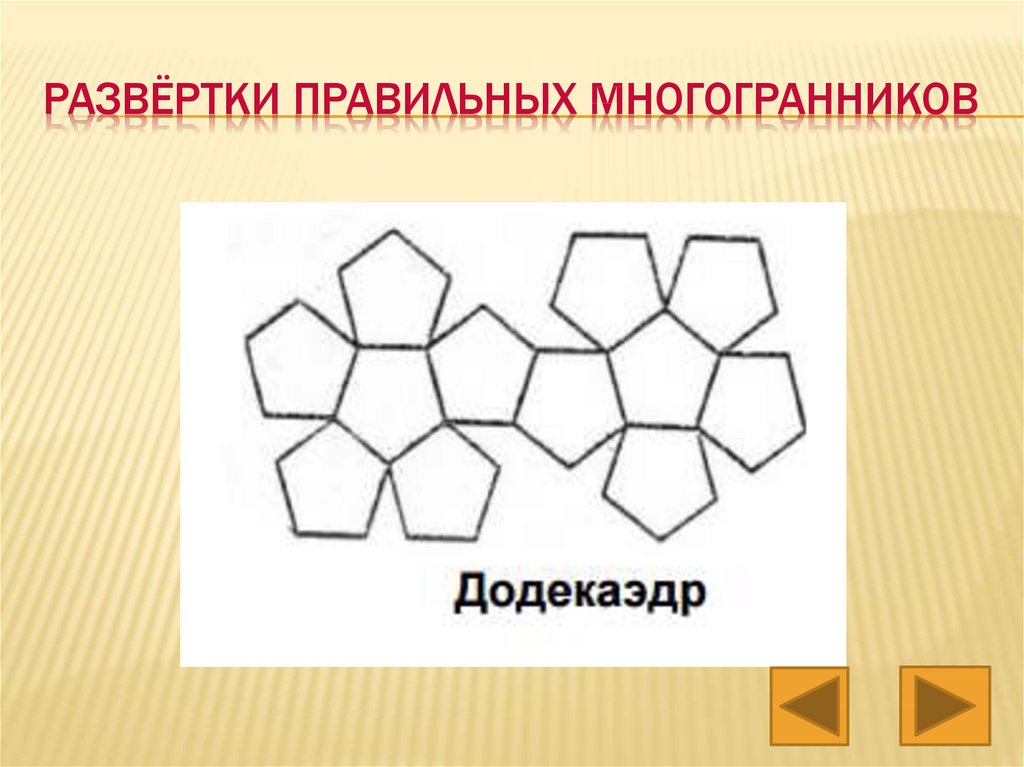
РАЗВЁРТКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ11. Теорема Эйлера
ТЕОРЕМА ЭЙЛЕРАГеометрия
грани
Тетраэдр
Гексаэдр
Октаэдр
Додекаэдр
Икосаэдр
Количество Количество Количество
вершин
рёбер
граней
4
8
6
6
12
12
4
6
8
20
12
30
30
12
20
В–Р+Г=2
12. ИЗ истории
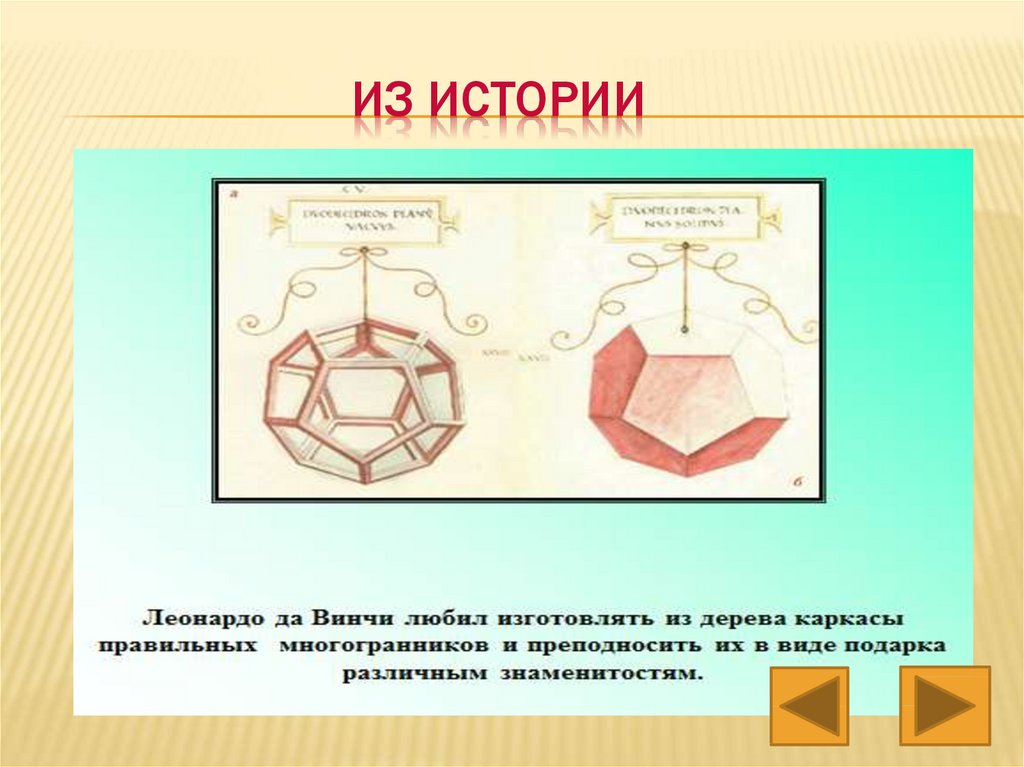
ИЗ ИСТОРИИ13. ИЗ истории
ИЗ ИСТОРИИ14. ИЗ истории
ИЗ ИСТОРИИ15. Правильные многогранники в природе
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ПРИРОДЕ16. Правильные многогранники в природе
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ПРИРОДЕ17. Правильные многогранники в природе
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ПРИРОДЕ18. Правильные многогранники в природе
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ В ПРИРОДЕ19.
«Правильных многогранников
вызывающе мало, но этот весьма
скромный по численности отряд сумел
пробраться в самые глубины различных
наук.»
Л. Кэрролл
20. Классная работа
КЛАССНАЯ РАБОТА21.
22. Задача № 3. Сторона основания правильной треугольной призмы равна 8 см, боковое ребро - 6 см. Найдите Sсеч, проходящего через
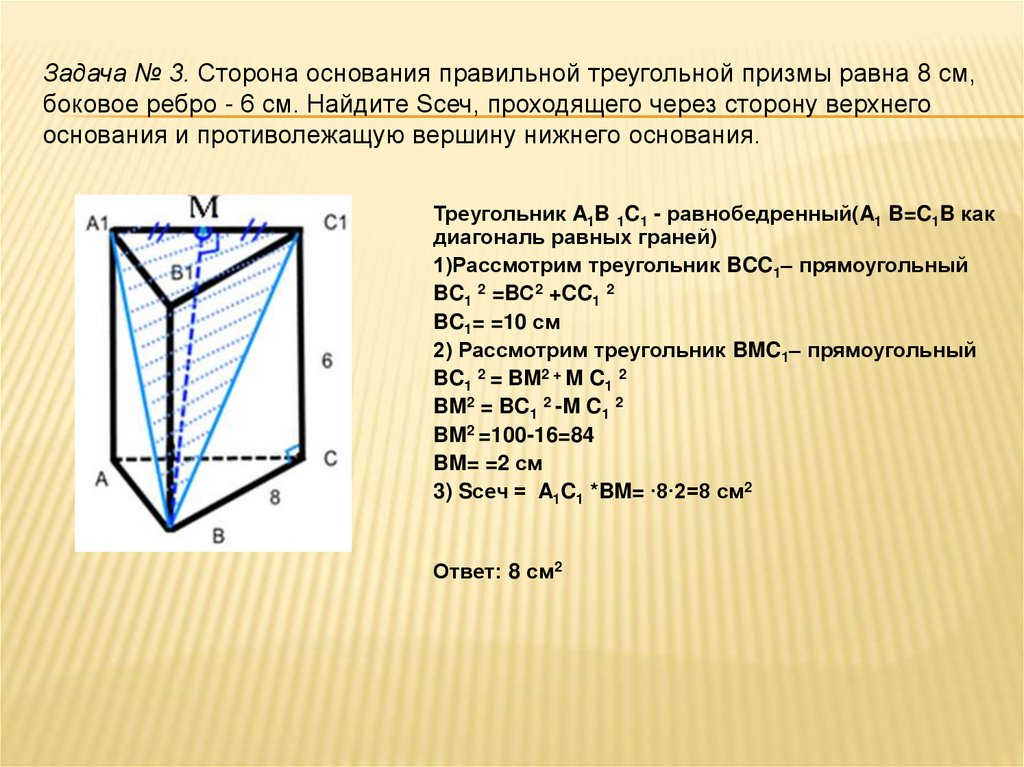
Задача № 3. Сторона основания правильной треугольной призмы равна 8 см,боковое ребро - 6 см. Найдите Sсеч, проходящего через сторону верхнего
основания и противолежащую вершину нижнего основания.
Треугольник A1B 1C1 - равнобедренный(A1 B=C1B как
диагональ равных граней)
1)Рассмотрим треугольник BCC1– прямоугольный
BC1 2 =BС2 +CC1 2
BC1= =10 см
2) Рассмотрим треугольник BMC1– прямоугольный
BC1 2 = BM2 + M C1 2
BM2 = BC1 2 -M C1 2
BM2 =100-16=84
BM= =2 см
3) Sсеч = A1C1 *BM= ∙8∙2=8 см2
Ответ: 8 см2
23. Задача № 1. Основанием прямой четырехугольной призмы является ромб с диагоналями 1,6 дм и 3 дм, боковое ребро призмы равно 10
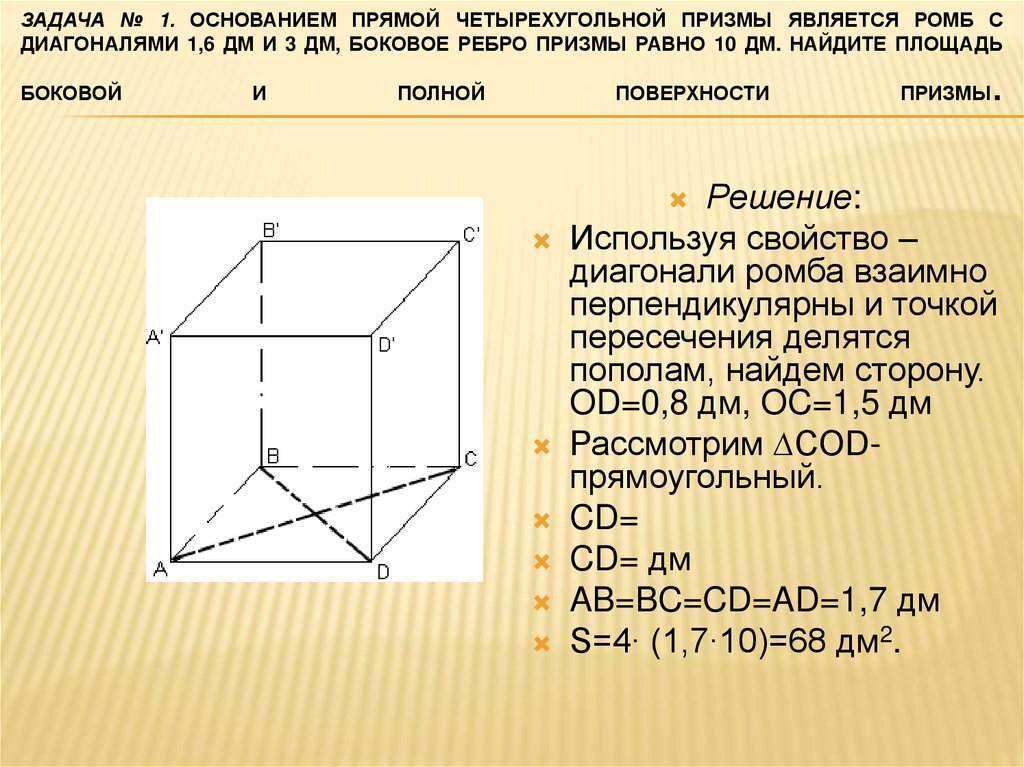
ЗАДАЧА № 1. ОСНОВАНИЕМ ПРЯМОЙ ЧЕТЫРЕХУГОЛЬНОЙ ПРИЗМЫ ЯВЛЯЕТСЯ РОМБ СДИАГОНАЛЯМИ 1,6 ДМ И 3 ДМ, БОКОВОЕ РЕБРО ПРИЗМЫ РАВНО 10 ДМ. НАЙДИТЕ ПЛОЩАДЬ
БОКОВОЙ
И
ПОЛНОЙ
ПОВЕРХНОСТИ
.
Решение:
Используя свойство –
диагонали ромба взаимно
перпендикулярны и точкой
пересечения делятся
пополам, найдем сторону.
OD=0,8 дм, OC=1,5 дм
Рассмотрим ∆СОDпрямоугольный.
CD=
CD= дм
AB=BC=CD=AD=1,7 дм
S=4∙ (1,7∙10)=68 дм2.
ПРИЗМЫ
24.
25.
26.
27. Домашнее задание
ДОМАШНЕЕ ЗАДАНИЕ1. Сторона правильной треугольной пирамиды
равна 6 см, а высота √13 см. Найдите площадь
боковой поверхности пирамиды.
2. Основание прямой призмы - ромб с острым
углом 60°. Боковое ребро призмы равно 10 см, а
площадь боковой поверхности - 240 см2. Найдите
площадь сечения призмы, проходящего через
боковое ребро и меньшую диагональ основания.



















 mathematics
mathematics








