Similar presentations:
Призма. Пирамида. Решение задач (9 класс)
1.
9 класс геометрияПризма. Пирамида.
Решение задач.
2. Учащийся достиг цели, если:
знает и применяет формулыплощадей призмы и пирамиды,
при решении задач;
знает и применяет формулы
объема призмы и пирамиды,
при решении задач
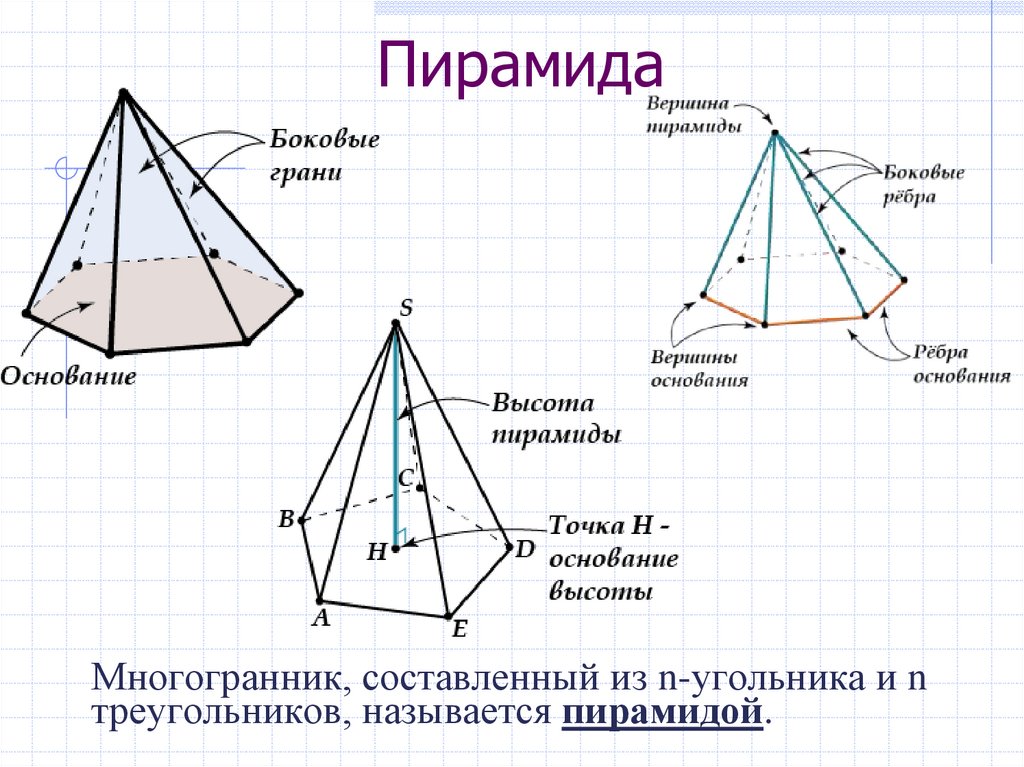
3. Пирамида
Многогранник, составленный из n-угольника и nтреугольников, называется пирамидой.
4.
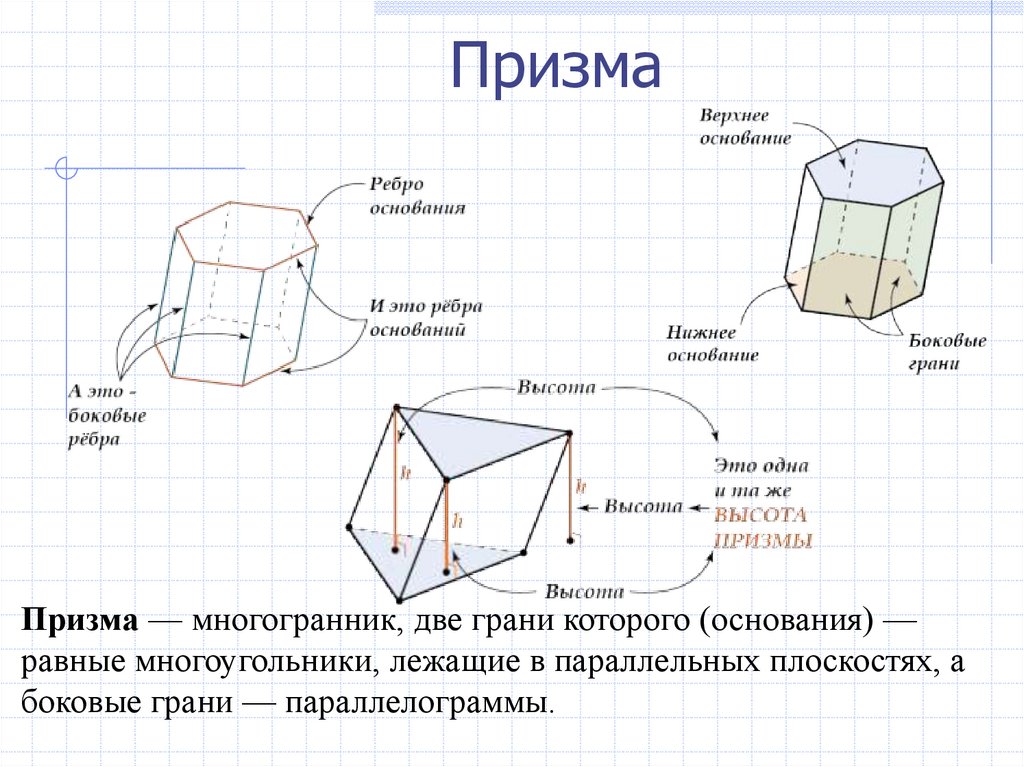
ПризмаПризма — многогранник, две грани которого (основания) —
равные многоугольники, лежащие в параллельных плоскостях, а
боковые грани — параллелограммы.
5.
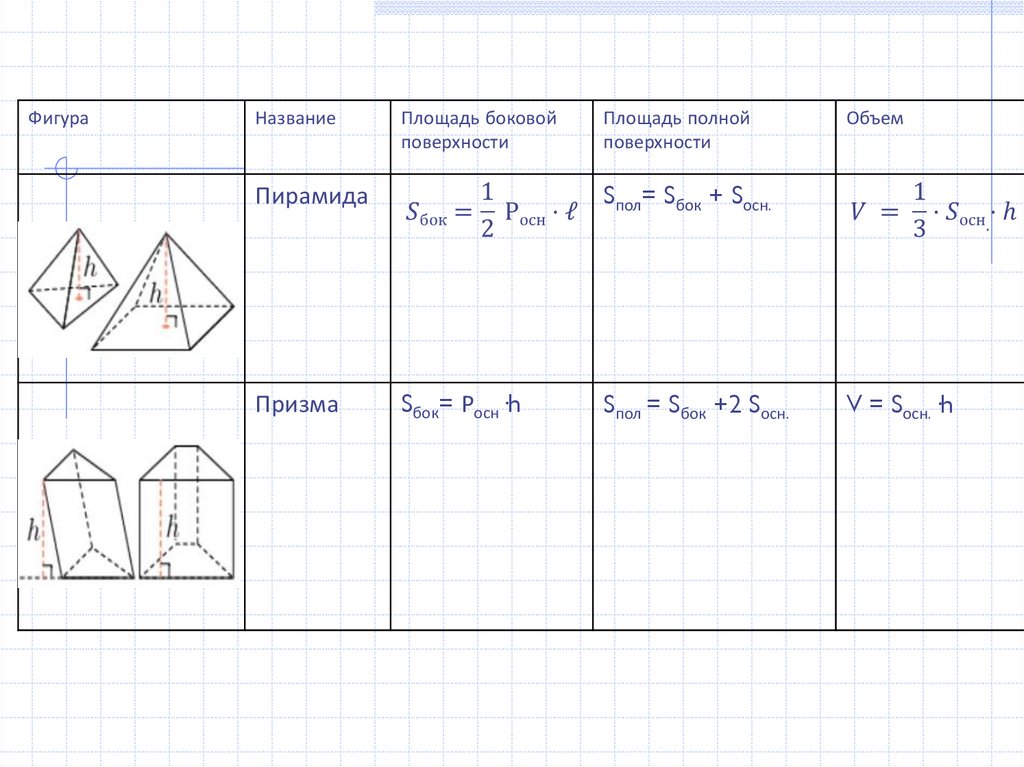
ФигураНазвание
Площадь боковой
поверхности
Объем
Sпол= Sбок + Sосн.
Пирамида
Призма
Площадь полной
поверхности
Sбок= Росн·h
Sпол = Sбок +2 Sосн.
V = Sосн.·h
6. Решим задачи
7.
Основанием прямой треугольной призмы служитпрямоугольный треугольник с катетами 6 и 8, высота призмы
равна 10. Найдите площадь ее поверхности.
Решение:
кв. ед.
8.
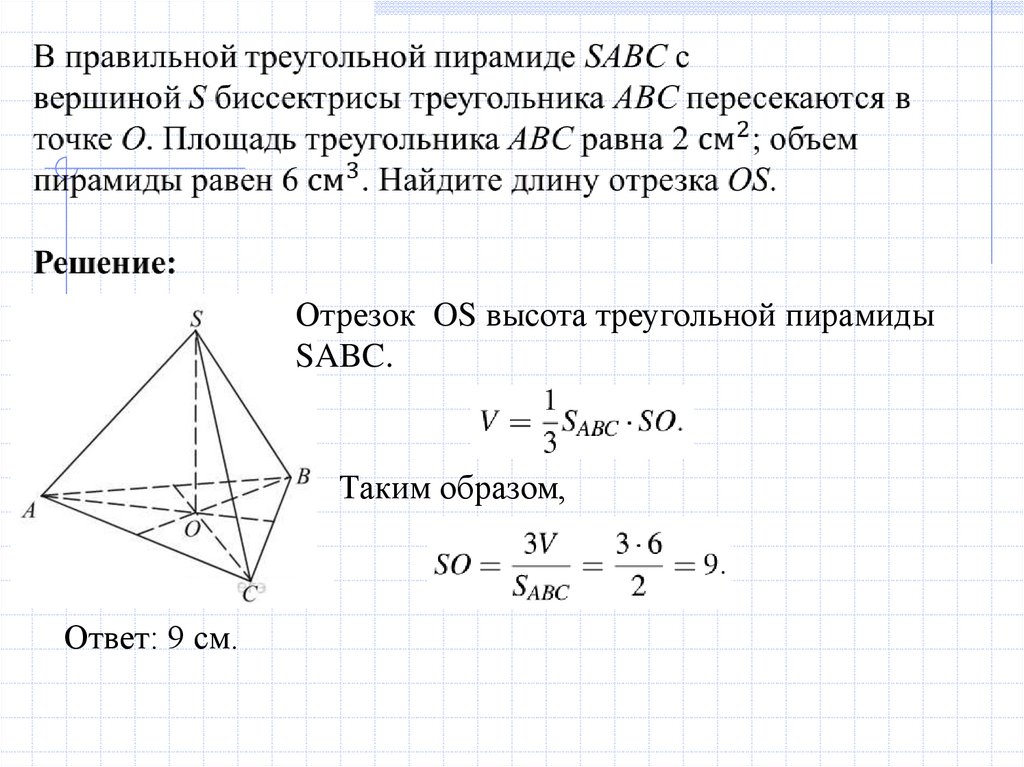
Отрезок OS высота треугольной пирамидыSABC.
Таким образом,
Ответ: 9 см.
9.
В правильной четырехугольной пирамиде SABCD точка O –центр основания, S – вершина, SO=15см , BD=16см. Найдите
боковое ребро SA.
Решение:
В правильной пирамиде вершина проецируется в
центр основания, следовательно, SO является
высотой пирамиды. Тогда по теореме Пифагора
Ответ: 17 см
10.
В правильной треугольной пирамиде SABC точка M – серединаребра AB, S – вершина. Известно, что BC = 3см, а площадь
боковой поверхности пирамиды равна 45 см. Найдите длину
отрезка SM.
Решение:
Найдем площадь грани SAB:
Ответ: 10 см.
11.
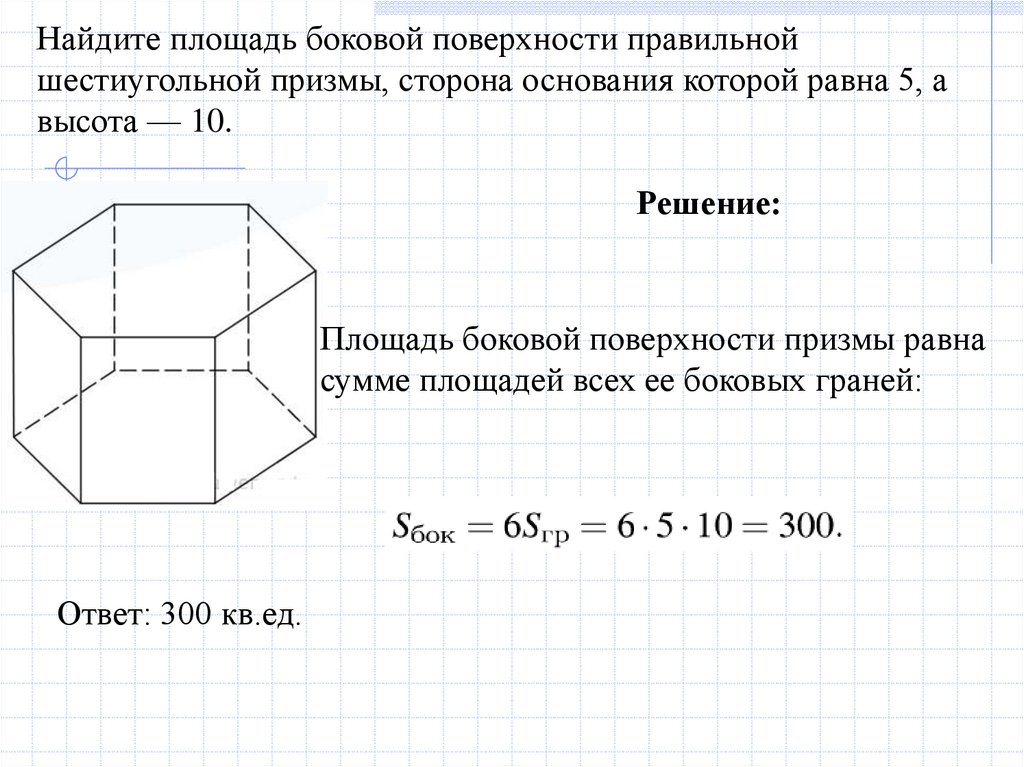
Найдите площадь боковой поверхности правильнойшестиугольной призмы, сторона основания которой равна 5, а
высота — 10.
Решение:
Площадь боковой поверхности призмы равна
сумме площадей всех ее боковых граней:
Ответ: 300 кв.ед.
12.
В прямой треугольной призме стороны основания равны 10 см,17 см и 21 см, а высота призмы — 18 см. Найдите площадь
сечения, проведенного через боковое ребро, и меньшую высоту
основания.
Решение:
BHH1B1 - сечение (прямоугольник), со
сторонами ВВ1=18 см и ВН; где ВН —
меньшая высота ΔАВС.
13.
2. Основанием прямой треугольнойпризмы служит прямоугольный
треугольник с катетами 3 и 4, высота
призмы равна 10. Найдите площадь ее
поверхности.
12 см








 mathematics
mathematics








