Similar presentations:
Лекция 4: 2-я основная задача линейной алгебры - Нахождение собственных значений и собственных векторов матрицы
1. Линейная алгебра Лекция 4: 2-я основная задача линейной алгебры - Нахождение собственных значений и собственных векторов
матрицы.Характеристическое уравнение матрицы. Нахождение
решения однородных СЛАУ. Свойства собственных
значений и собственных векторов матрицы. Линейно
зависимые вектора. Вычисление детерминанта матрицы
по значениям её собственных чисел.
Лектор: доцент Горяйнов В.А.
2024
2. Где встречаются задачи на собственные вектора 1 и собственные значения матриц С задачами на собственные вектора и собственные
3. Собственные значения и собственные векторы 2 матрицы. Определения.
Собственные значения и собственные векторыматрицы. Определения.
(1)
(2)
Однородная СЛАУ
2
4. Характеристическое уравнение матрицы 3
5.
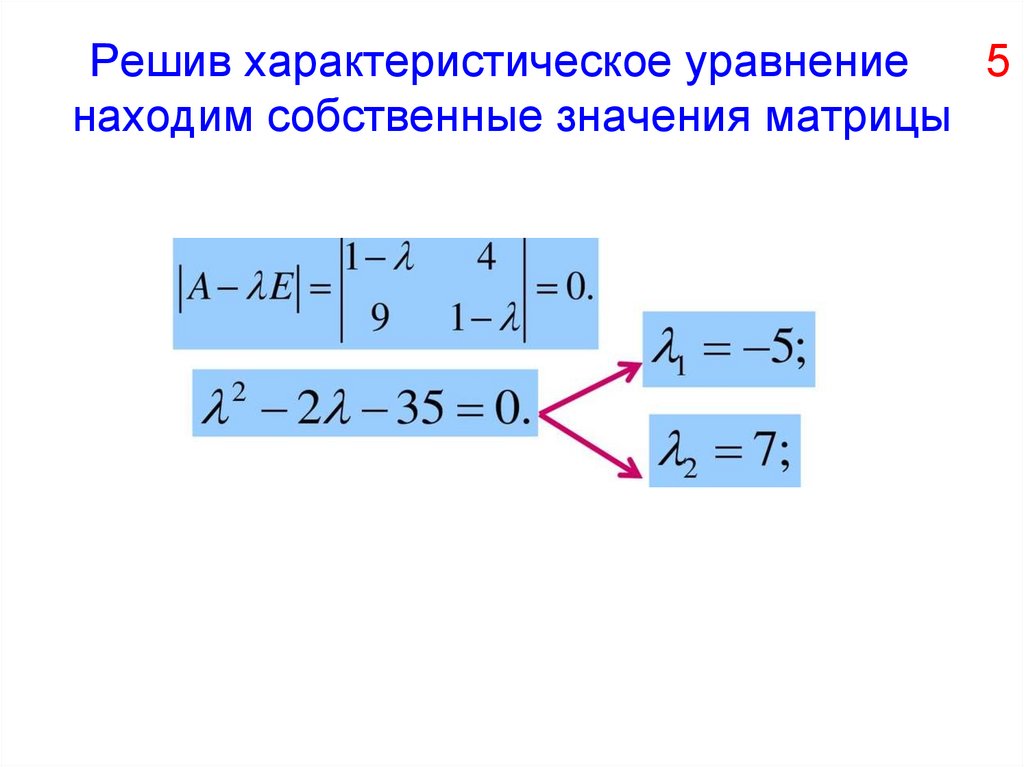
6. Решив характеристическое уравнение 5 находим собственные значения матрицы
7. Повторим тоже для матрицы 3х3 6
8. Однородная СЛАУ в развёрнутом виде 7
9. 8
10. Пример 1 нахождения собственного значения 9 для матрицы 3-го порядка
Пример 1 нахождения собственного значениядля матрицы 3-го порядка
9
11. Пример 2 для матрицы 3-го порядка 10 с кратными собственными значениями
Пример 2 для матрицы 3-го порядкас кратными собственными значениями
10
12. 11
13. Пример решения однородной СЛАУ 12
3. Проведём элементарные преобразования:1. Дана однородная СЛАУ
Ко 2-ой строчке прибавим 1-ую умноженную на (-3);
К 3-ей строчке прибавим 1-ую умноженную на (-2);
Получили эквивалентную матрицу и соответствующую
равносильную (исходной) систему уравнений.
Видим, что 2-е и 3-е уравнение – линейно зависимые
2. Выпишем матрицу
системы
4. Далее к 1-ой строчке прибавим 2-ую, умноженную на (2),
ко 2-ой прибавим 3-ью, умноженную на (-2), а 3-ью умножим
на (-1)
В результате 2-я строчка обнулилась и мы получили
равносильную (исходной) систему 2-х уравнений с 3-мя
неизвестными:
14.
Пример 2 для матрицы 3-го порядка (со слайда 10)с нахождением собственных векторов
13
Имеем три СЛАУ для нахождения
3-х собственных векторов:
А1 Х1 = 0
А2 Х2 = 0
А3 Х3 = 0
Матрицы А1 и А2 равны, т.к. λ1= λ2
В случае λ1=1 полагаем с1=1, а с2=0,
в случае λ2=1 полагаем с1=0, а с2=1.
В случае λ3=3 полагаем с1=1.
Имеем право, т.к. с1 и с2 –
произвольные константы.
15. 14 Свойства собственных значений и собственных векторов матрицы
16. 1
17. 16
Пропорциональные вектора всегда являются линейно зависимыми. И,наоборот, два линейно зависимых вектора всегда пропорциональны,
т.е. имеют одинаковое направление (коллинеарные).
18. 17
19. 18
20. Матрица с нулевым собственным значением 19 Здесь единичная матрица обозначена буквой I
Матрица с нулевым собственным значениемЗдесь единичная матрица обозначена буквой I
19
21. Матрица с нулевым собственным значением 20 (продолжение)
Матрица с нулевым собственным значением(продолжение)
20





















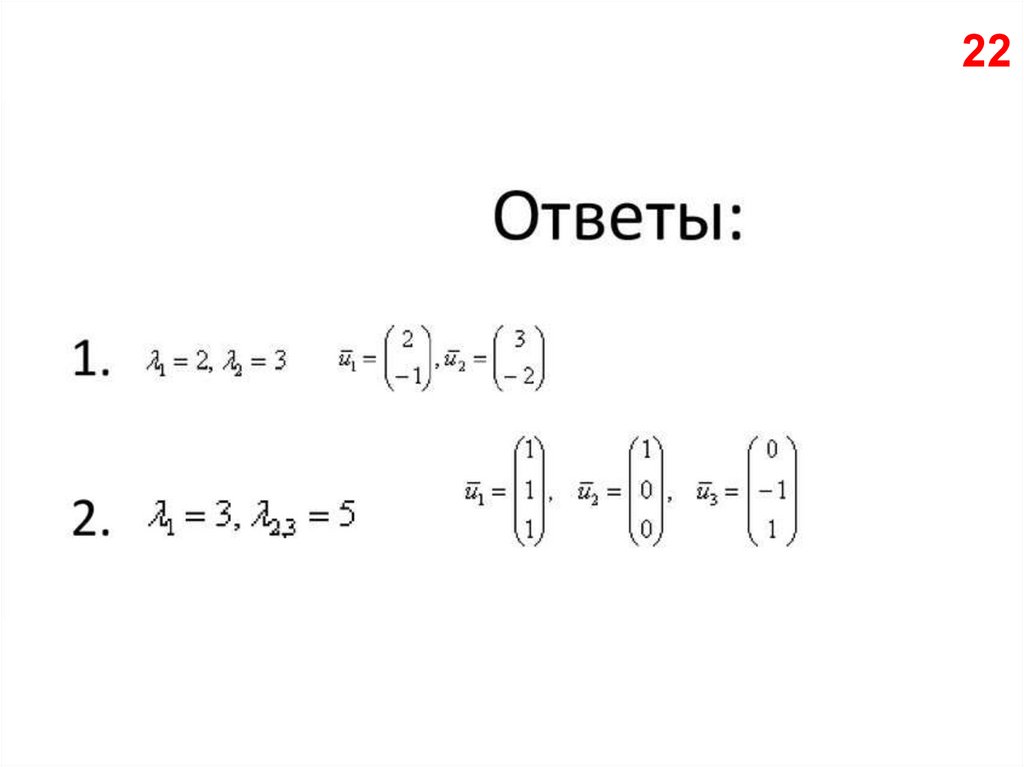




 mathematics
mathematics








