Similar presentations:
Techniques of integration
1. TECHNIQUES OF INTEGRATION
Trigonometric SubstitutionIn this section, we will learn about:
The various types of trigonometric substitutions.
2. TRIGONOMETRIC SUBSTITUTION
3.
4.
Notice the difference between the substitution u = a2 – x2 and thesubstitution x = a sin θ.
In the first, the new variable is a function of
the old one.
In the second, the old variable is a function of
the new one.
In general, we can make a substitution of the form x = g(t)
by using the Substitution Rule in reverse.
To make our calculations simpler, we assume g
has an inverse function, that is, g is one-to-one.
5. INVERSE SUBSTITUTION
Here, if we replace u by x and x by t in the Substitution Rulewe obtain:
This kind of
substitution
is
called
inverse
substitution.
We can make the inverse
substitution x = a sin θ, provided
that it defines
a one-to-one
function.
This can be accomplished
by restricting θ to lie in the
interval
[-π/2, π/2].
6. TABLE OF TRIGONOMETRIC SUBSTITUTIONS
Here, we list trigonometric substitutions that are effective for thegiven radical expressions because of the specified trigonometric
identities.
7. TABLE OF TRIGONOMETRIC SUBSTITUTIONS
In each case, the restriction on θ is imposed to ensure that thefunction that defines the substitution is one-to-one.
These are the same intervals used to defining
the inverse functions.
8. TRIGONOMETRIC SUBSTITUTION
Example 19.
Thus, the Inverse Substitution Rule gives:Example 1
As this is an
indefinite integral,
we must return to
the original
variable x. This
can be done in
either of two ways.
One, we can use
trigonometric identities to
express cot θ in terms
of
sin θ = x/3.
Two, we can draw a diagram, where
θ is interpreted as an angle of a right
triangle.
10. TRIGONOMETRIC SUBSTITUTION
Example 1Since sin θ = x/3, we label the opposite side and the hypotenuse as
having lengths x and 3.
Although θ > 0 here,
this expression for
cot θ is valid even
when θ < 0.
As sin θ = x/3, we have θ = sin-1(x/3).
Hence,
11. TRIGONOMETRIC SUBSTITUTION
Solution:or
Example 2
12.
SolutionAs the ellipse is symmetric with respect to both axes, the total area A
is four times the area in the first quadrant.
13.
SolutionTo evaluate this integral, we substitute
x = a sin θ.
Then,
dx = a cos θ dθ.
To change the limits of integration,
we note that:
When x = 0, sin θ = 0;
so θ = 0
When x = a,
so θ = π/2
sin θ = 1;
Also, since 0 ≤ θ ≤ π/2,
14.
Therefore,We have shown that the area of
an ellipse with semi-axes a and b
is
A=πab.
In particular, taking a =
b = r, we have proved
the famous formula
that the area of a circle
with radius r is πr2.
15.
Example 3Solution:
Thus, we have:
16.
To evaluate this trigonometric integral, we put everything in terms of sinθ and cos θ:
Therefore, making the
substitution u = sin θ, we
have:
17.
We use the figure to determine that:Hence,
18.
Example 4Solution
It
would be possible to use the
trigonometric substitution x = 2 tan θ;
However, the direct substitution u = x2 + 4
is simpler. Then, du = 2x dx
Note
Example 4 illustrates the fact that, even
when trigonometric substitutions are
possible, they may not give the easiest
solution.
You should look for a
simpler method first.
19.
Example 5Solution-1
We let x = a sec θ, where 0 < θ < π/2 or π < θ < π/2. Then,
dx = a sec θ tan θ dθ
and
20.
Therefore,21.
The triangle in the figure gives:So, we have:
22.
Solution 2For x > 0, the hyperbolic substitution x = a cosh t can
also be used.
Using the identity cosh2y – sinh2y = 1, we have:
23.
Sincedx = a sinh t dt, we obtain:
Since cosh t = x/a, we have t = cosh-1(x/a)
and
Although Formulas
1 and 2 look quite
different, they are
actually equivalent
24.
Example 6Solution
So, trigonometric substitution is appropriate.
25.
However, it becomes one if we make thepreliminary substitution u = 2x.
When we combine this with the tangent substitution, we have:
and
26.
Thus:27.
Now, we substitute u = cos θso that
When θ = 0, u = 1.
Therefore
When θ = π/3, u = ½.
du = - sin θ dθ.
28.
Example 7Solution
We can transform the integrand into a function for
which trigonometric substitution is appropriate, by first
completing the square under the root sign:
29.
This suggests we make the substitutionThen,
So,
This gives
du = dx
and
u = x + 1.
x = u – 1.
30.
So,
31.
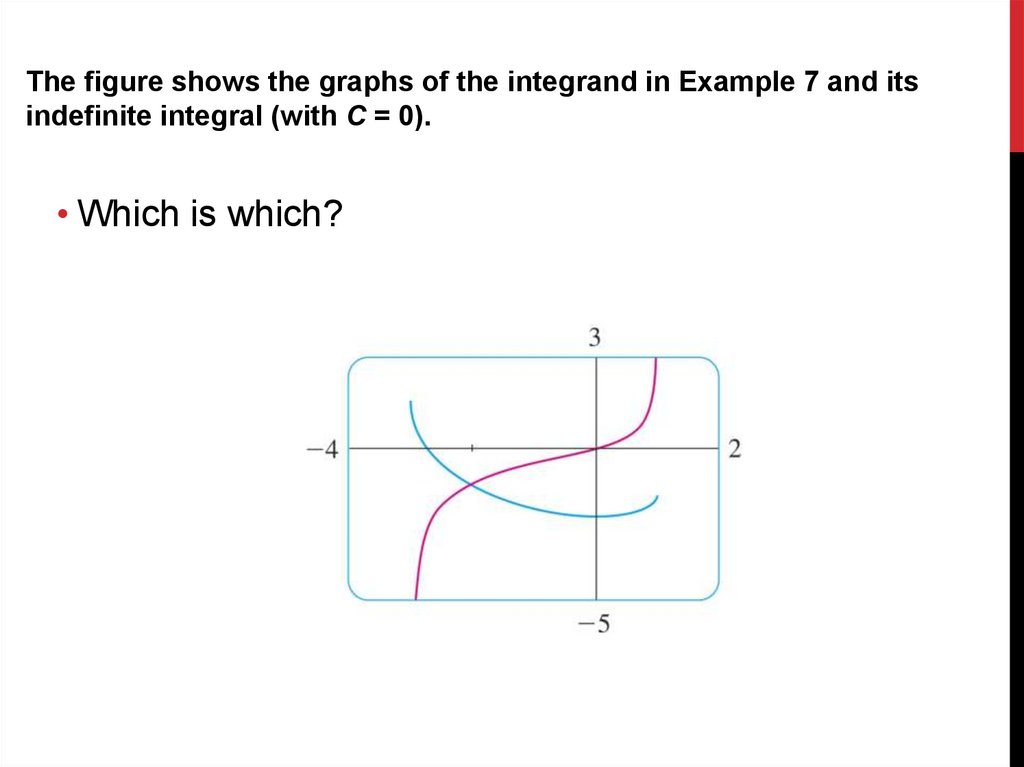
The figure shows the graphs of the integrand in Example 7 and itsindefinite integral (with C = 0).
• Which is which?



















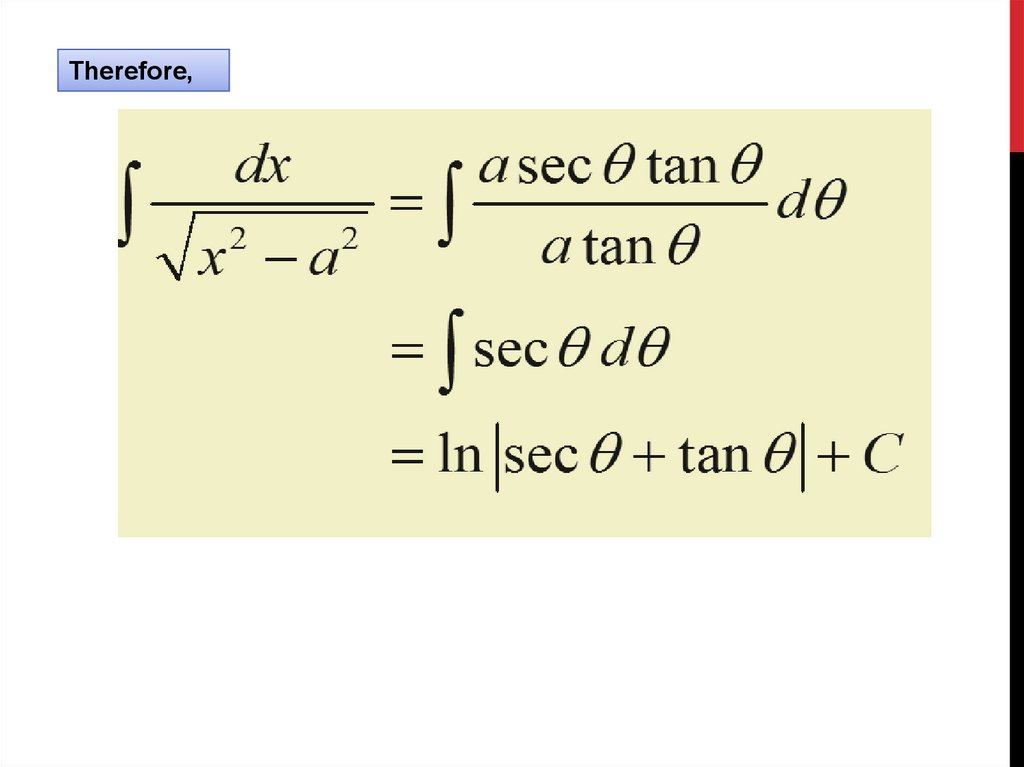










 mathematics
mathematics








