Призма, её элементы и свойства

1. ПРИЗМА, её элементы и свойства

2. Понятие призмы

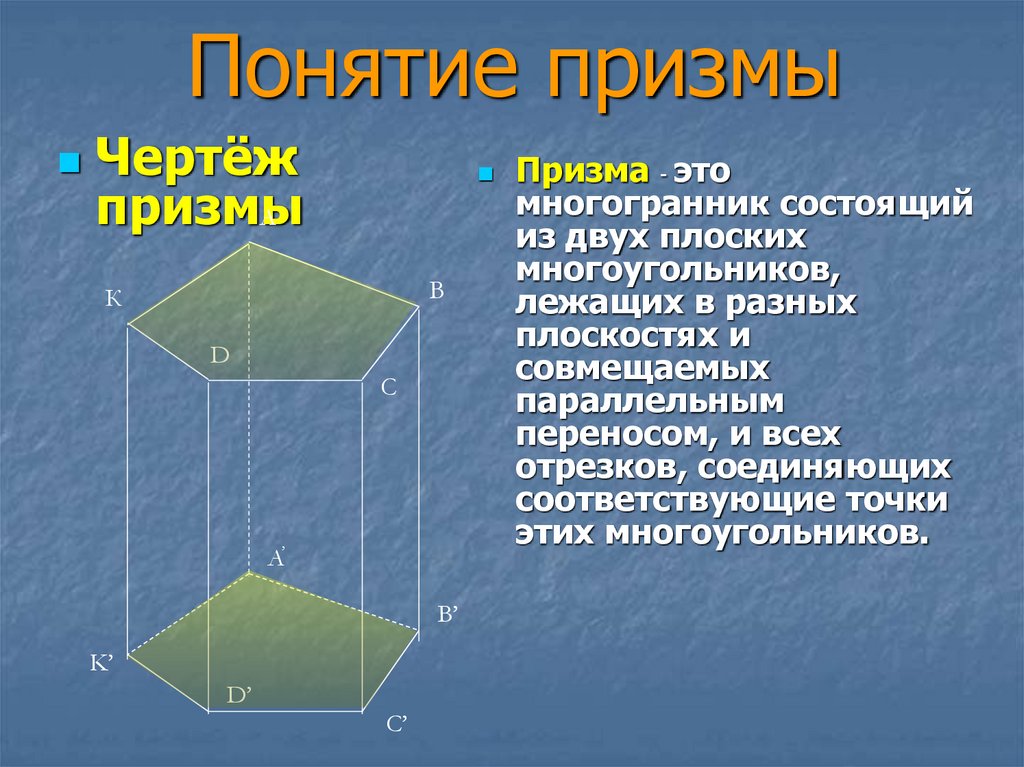
Чертёж
призмы
А
В
К
D
С
A’
B’
K’
D’
C’
Призма - это
многогранник состоящий
из двух плоских
многоугольников,
лежащих в разных
плоскостях и
совмещаемых
параллельным
переносом, и всех
отрезков, соединяющих
соответствующие точки
этих многоугольников.

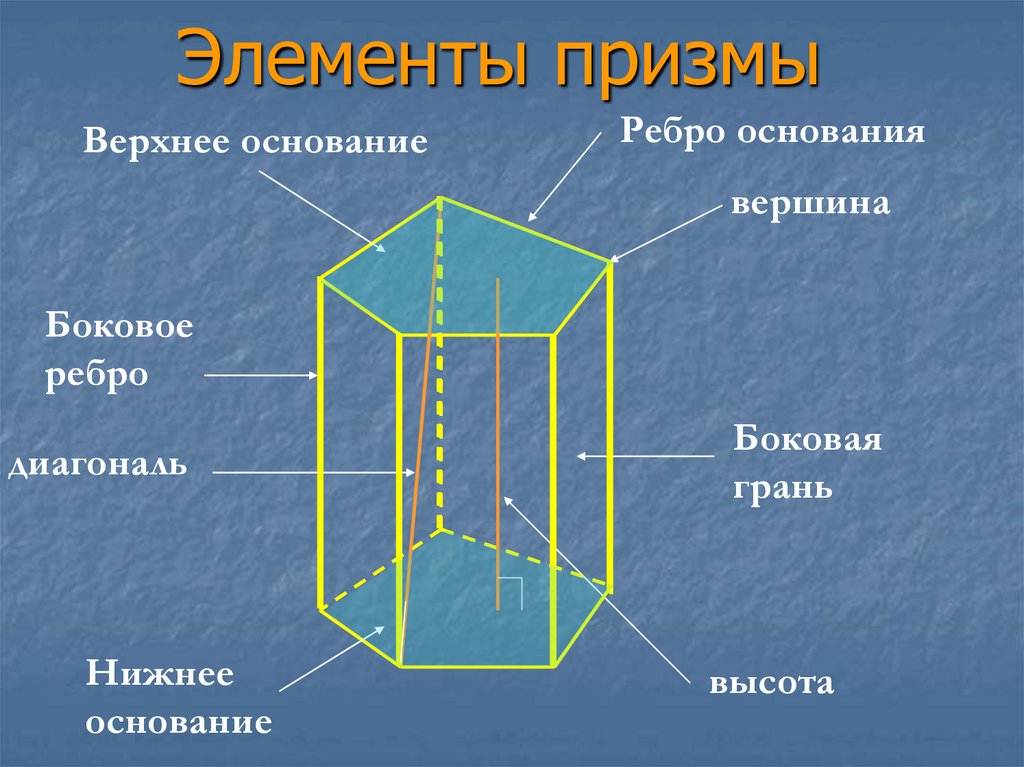
3. Элементы призмы

Верхнее основание
Ребро основания
вершина
Боковое
ребро
диагональ
Нижнее
основание
Боковая
грань
высота

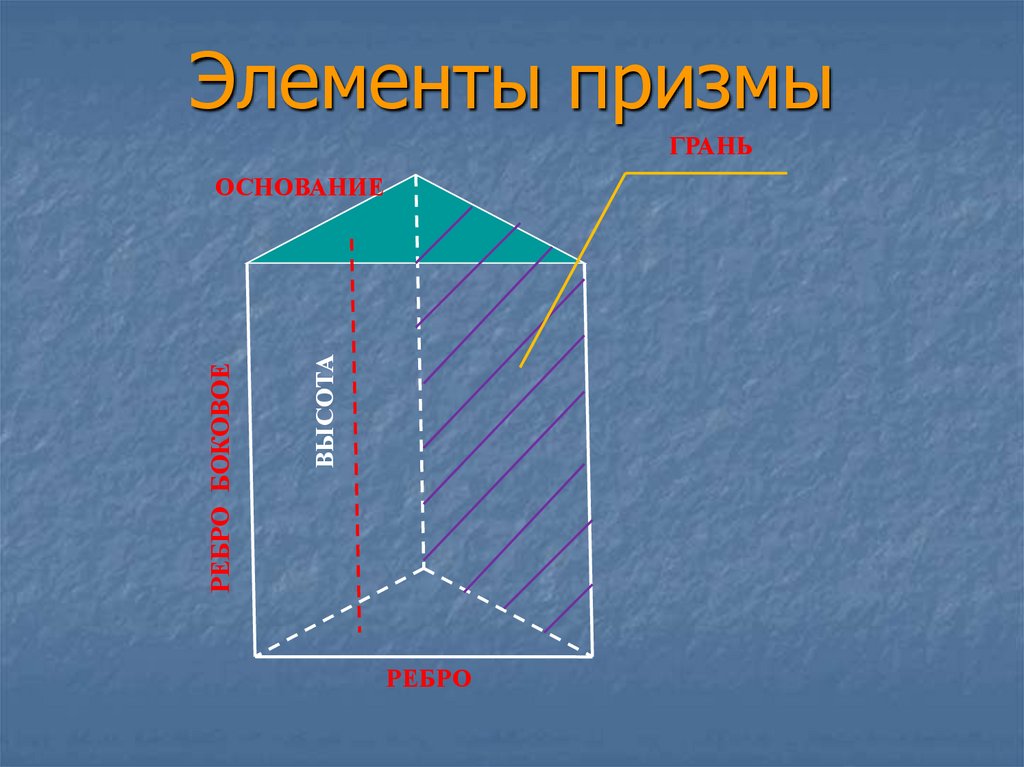
4. Элементы призмы

ГРАНЬ
ВЫСОТА
РЕБРО БОКОВОЕ
ОСНОВАНИЕ
РЕБРО

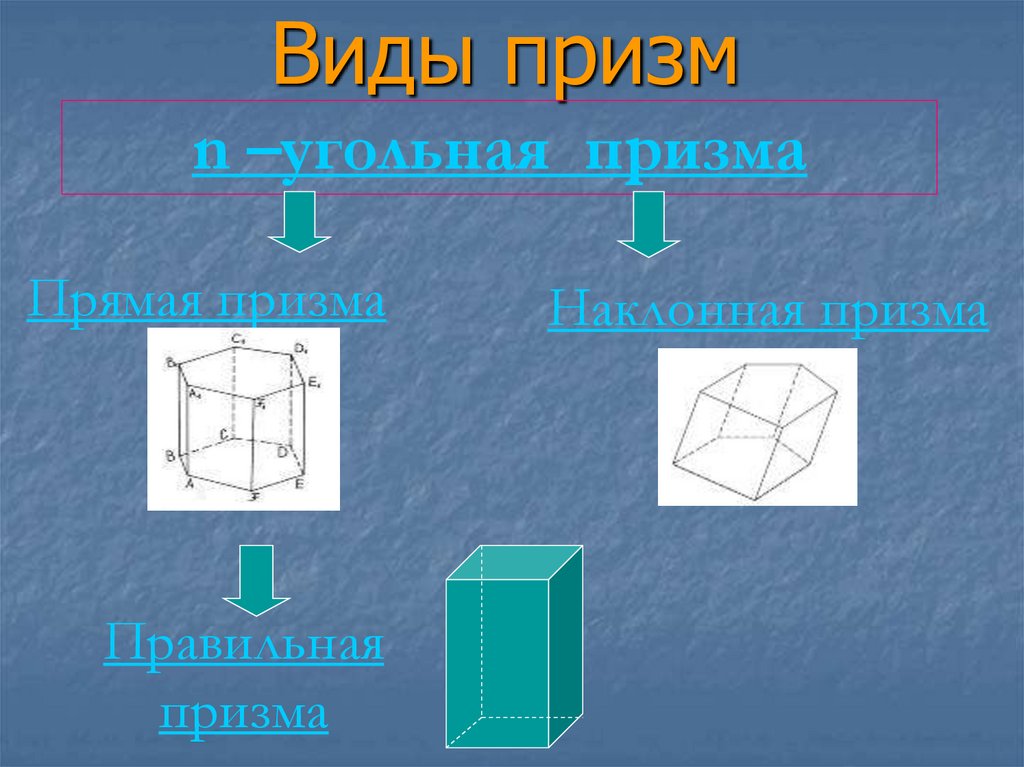
5. Виды призм

n –угольная призма
Прямая призма
Правильная
призма
Наклонная призма

6. Элементы призмы

Основания –
это грани, совмещаемые параллельным переносом.
Боковая грань –
это грань, не являющаяся основанием.
Боковые рёбра –
это отрезки, соединяющие соответствующие вершины
оснований.
Вершины –
это точки, являющиеся вершинами оснований.
Высота –
это перпендикуляр, опущенный из одного основания на другое.
Диагональ –
это отрезок, соединяющий две вершины, не лежащие в одной
грани.

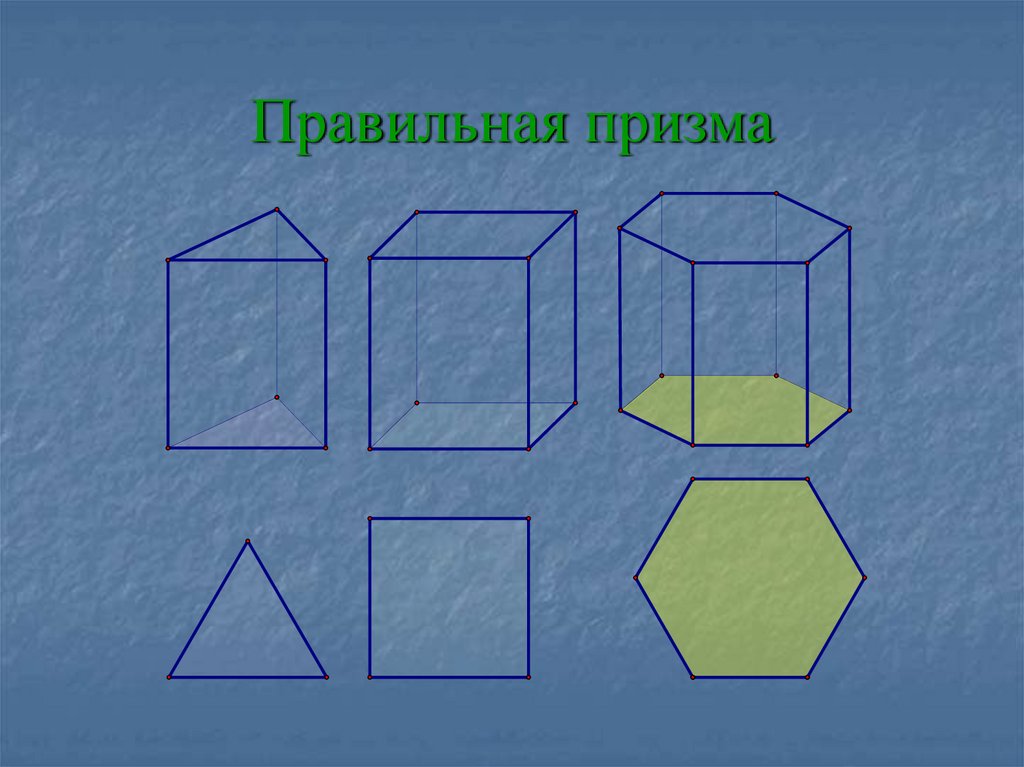
7. Правильная призма

8. виды призм

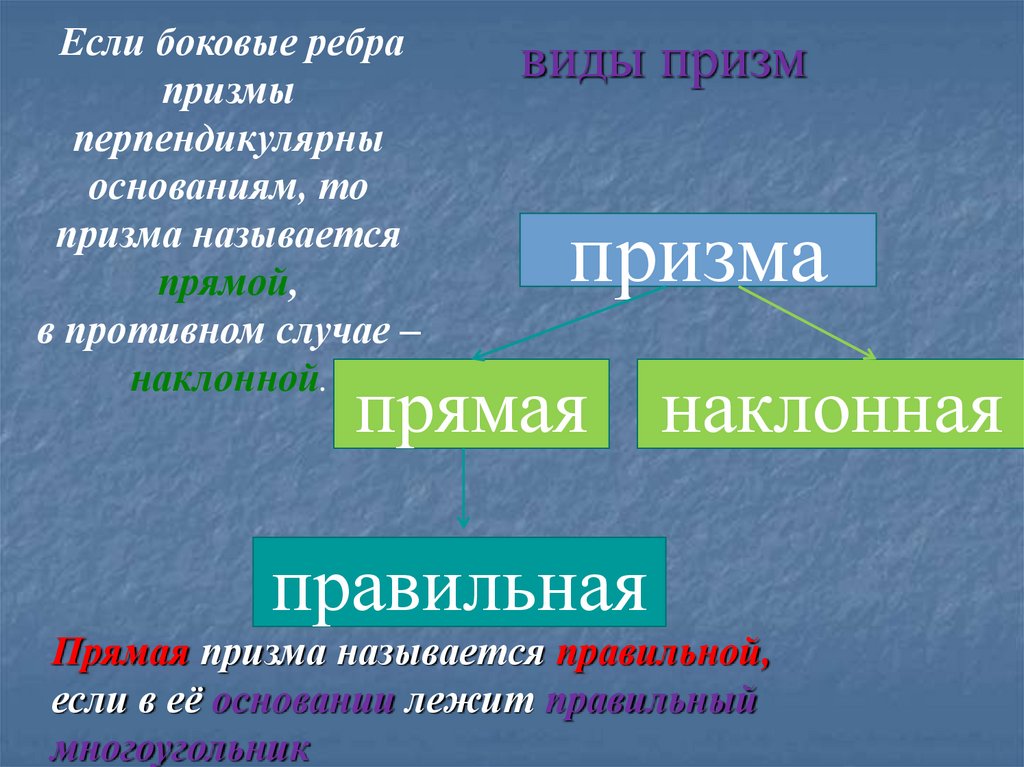
Если боковые ребра
призмы
перпендикулярны
основаниям, то
призма называется
прямой,
в противном случае –
наклонной.
виды призм
призма
прямая наклонная
правильная
Прямая призма называется правильной,
если в её основании лежит правильный
многоугольник

9.

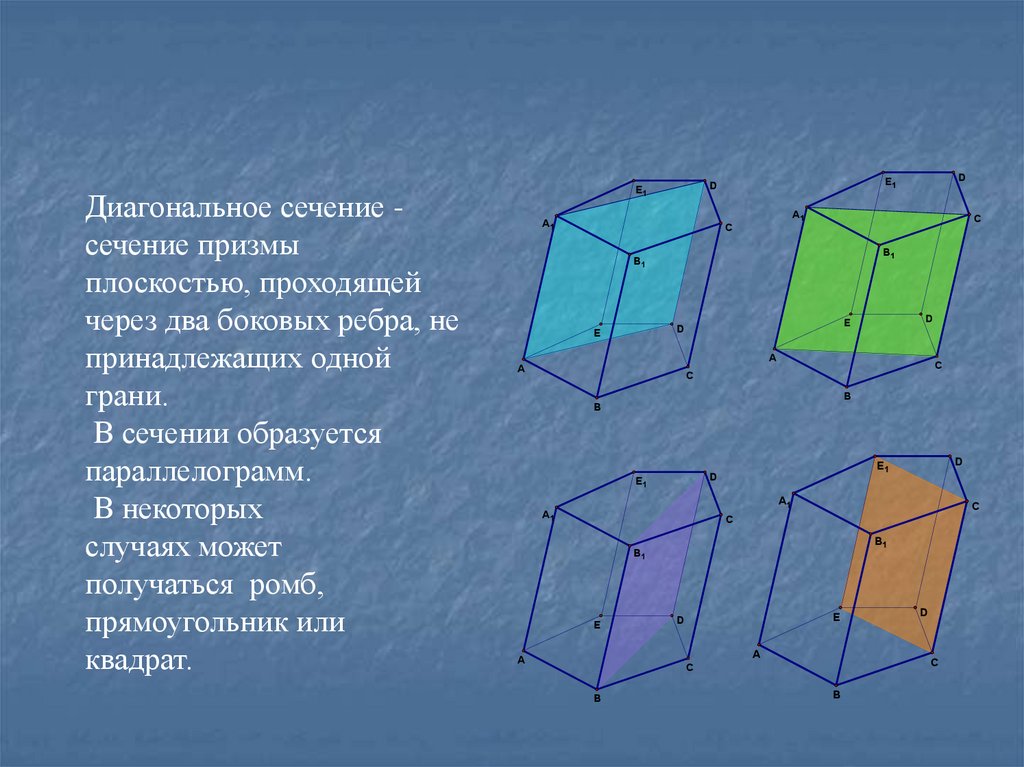
Диагональное сечение сечение призмы
плоскостью, проходящей
через два боковых ребра, не
принадлежащих одной
грани.
В сечении образуется
параллелограмм.
В некоторых
случаях может
получаться ромб,
прямоугольник или
квадрат.
D
E1
D
E1
A1
A1
C
C
B1
B1
D
E
D
E
A
A
C
C
B
B
E1
D
E1
D
A1
A1
C
C
B1
B1
E
E
D
A
A
C
C
B
D
B

10. . Площадь боковой поверхности призмы

Теорема о площади боковой поверхности
прямой призмы
Площадь боковой
поверхности прямой призмы
равна произведению периметра
основания на высоту призмы
Sбок Pосн H
P - периметр
h – высота призмы

11. Площадь полной поверхности призмы

Площадью полной
поверхности призмы
называется сумма
площадей всех ее граней.
Sполн Sбок 2Sосн

12. Объем призмы

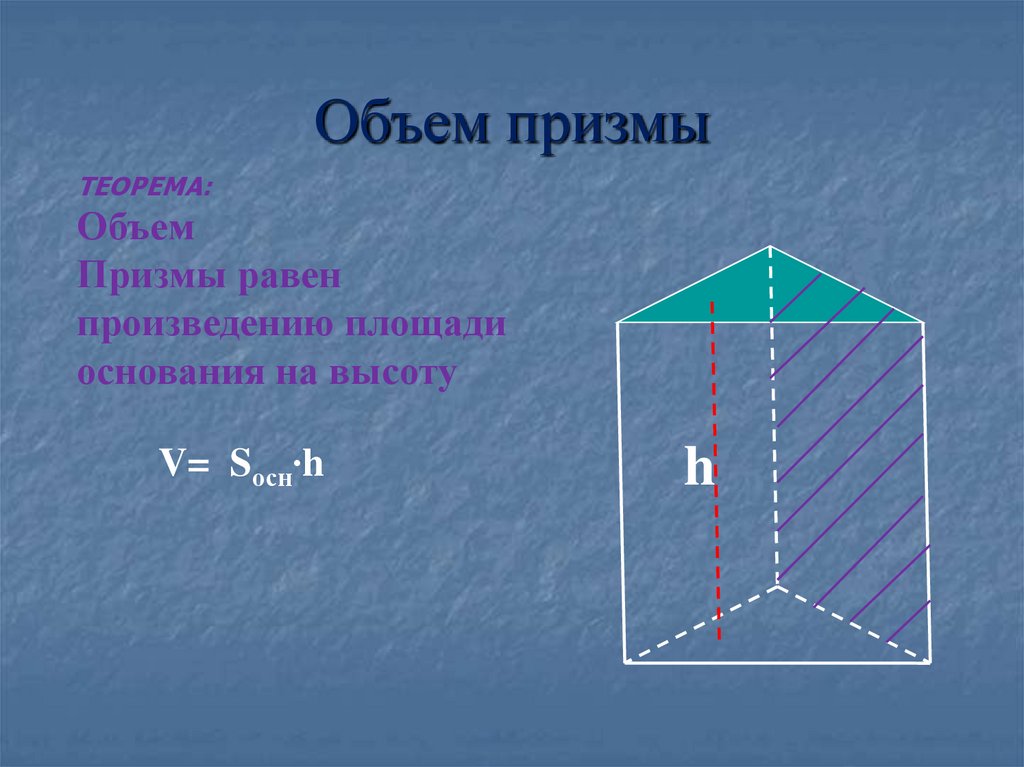
ТЕОРЕМА:
Объем
Призмы равен
произведению площади
основания на высоту
V= Sосн∙h
h

13.

Задача № 1
В правильной n-угольной призме сторона основания равна
а и высота равна h. Вычислите площади боковой и полной
поверхности призмы, если: n = 4, а = 12 дм, h = 8 дм.
Дано: n = 4
а = 12 дм
h = 8 дм
Решение:
Найти:
Sбок = Росн · h
Sбок– ?
Sбок = 4· 12 · 8 = 384 (дм2)
Sпол – ?
Sпол = Sбок + 2Sосн
Sосн = а2 = 122 = 144 (дм2)
Sпол= 384 + 2 · 144 = 672 (дм2)
Ответ: 384 дм2, 672 дм2