Условия равновесия плоской системы сил

1.

4. Условия равновесия плоской
системы сил
для равновесия произвольной плоской системы
сил необходимо и достаточно чтобы ее главный
вектор и главный момент были равны нулю
R R R
2
x
2
y
Rx Fkx
Ry
Fky
M o mo Fk
n
R=0
MO= 0
n Fkx 0
n Fky 0
n mo ( Fk ) 0
Для равновесия плоской системы сил необходимо и
достаточно, чтобы суммы проекций этих сил на каждую
координатную ось, а также сумма их моментов
относительно любого центра, находящегося в этой же
плоскости, были равны нулю

2.

Для равновесия плоской системы сил
необходимо и достаточно, чтобы суммы
их моментов относительно двух
произвольно выбранных центров А и В, и
сумма проекций всех сил на ось x, не
перпендикулярную к прямой, проходящей
через эти центры, были равны нулю
n mA ( Fk ) 0
n mB ( Fk ) 0
n Fkx 0
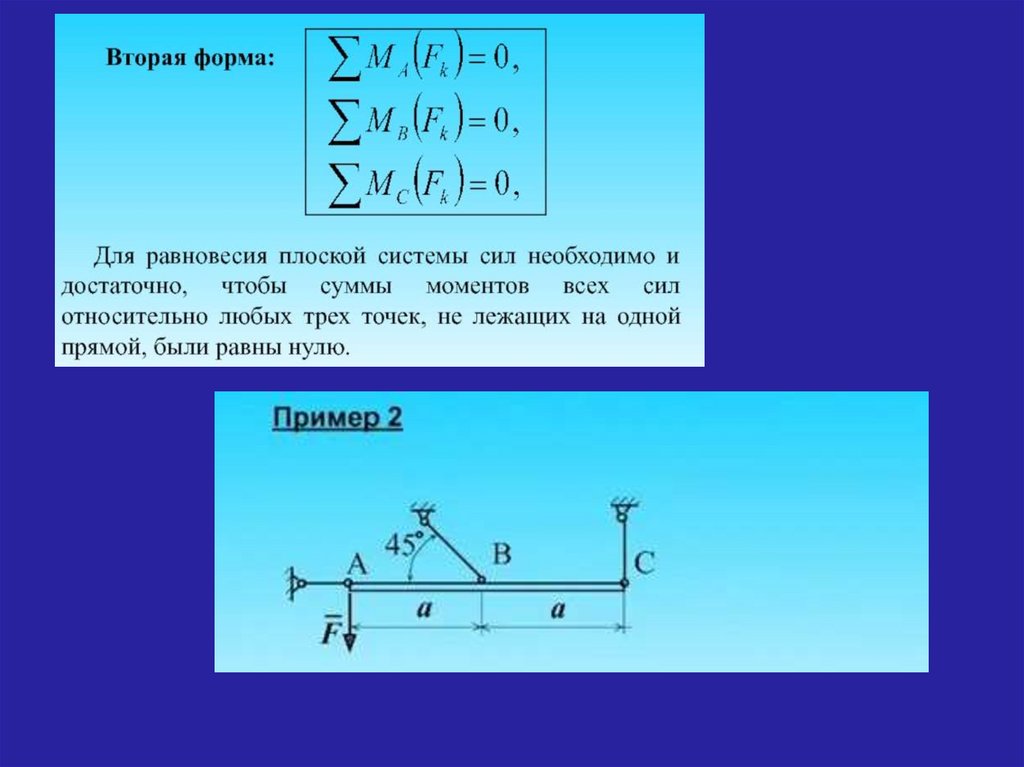
Для равновесия плоской системы сил
необходимо и достаточно, чтобы
суммы их моментов относительно трех
центров, не лежащих на одной прямой,
были равны нулю
n m A ( Fk ) 0
n mB ( Fk ) 0
n mC ( Fk ) 0
Задача о равновесии системы сил
Прямая:
будет ли заданная система сил являться уравновешенной
Обратная:
найти неизвестные силы, входящие в данную уравновешенную
систему сил

3.

Для того, чтобы задача была статически определенной, число
неизвестных не должно превышать числа возможных равнений
равновесия.
В инженерных расчетах часто приходится встречаться с нагрузками,
распределенными по определенному закону вдоль линии , поверхности или в
объеме. Распределенная нагрузка характеризуется интенсивностью q, т.е. величиной
силы, приходящейся на единицу длины, площади или объема.
Например, на рисунке (а),
приведена равномерно распределенная по
длине AB нагрузка интенсивностью q, измеряемая в Н/м. Эта нагрузка может быть
заменена сосредоточенной силой
Q = q ∙ AB [Н],
приложенной в середине отрезка AB.
На рисунке (б), показана равномерно убывающая (возрастающая) нагрузка по
линейному закону, которая может быть заменена равнодействующей силой
Q = qmax ∙ AB/2,
приложенной в точке C, причем AC = 2/3AB.

4.

5.

6.

7.

8.

9.

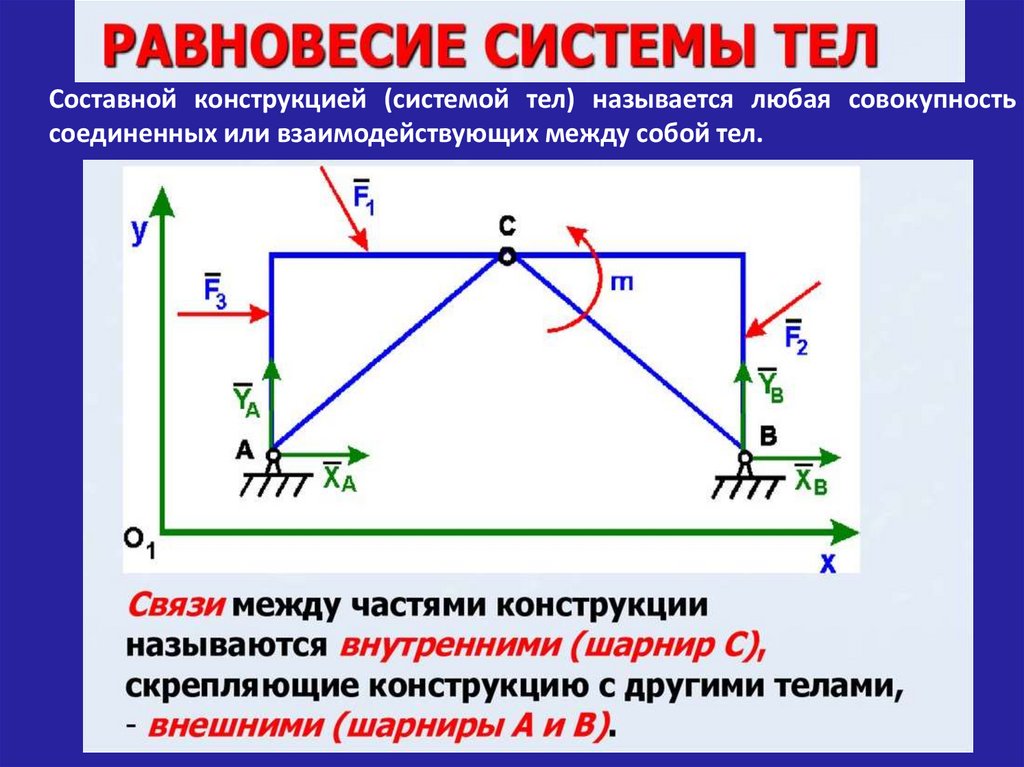
Составной конструкцией (системой тел) называется любая совокупность
соединенных или взаимодействующих между собой тел.

10.

При решении задач на равновесие системы сил может оказаться, что
число уравнений равновесия составной конструкции в целом меньше
чем число неизвестных сил.
Способ решения подобных задач заключается в том, что конструкцию
расчленяют на отдельные тела и рассматривают равновесие каждого из
этих тел. При этом реакции внутренних связей системы будут внешними
по отношению к отдельным тел. Они будут попарно равными по модулю
и противоположными по направлению.