Тригонометрия проект

1.

ПРОЕКТНАЯ
РА Б О ТА Н А
ТЕМУ:
ТРИГОНОМЕТРИ
Я
И З У Ч Е Н И Е О С Н О В И
П Р И М Е Н Е Н И Е
Т Р И Г О Н О М Е Т Р И И
Подготовили ученицы 9е класса :
Махаматкулова Севара
Козимова Зебо
Одилова Амаль
Икрамова Муслима
Проверила: Хаитбаева
Ш.Т

2.

ЦЕ ЛЬ
ПРЕЗЕНТАЦИИ
Познакомиться с основами
тригонометрии
Понять ,как применять
тригонометрические функции в
геометрии и физике
Рассмотреть реальные примеры
использования тригонометрии

3.

Ч Т О ТА К О Е
ТРИГОНОМЕТРИЯ
• Тригонометрия –это раздел математики , изучающий соотношения
между сторонами и углами треугольников.
Основные понятия :
• Синус (sin)
• Косинус(cos)
• Тангенс(tga)
• Котангенс(ctga)

4.

ОСНОВНЫЕ
ТРИ ГОН ОМЕТРИ ЧЕС КИ Е ФУ Н КЦИ И
• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.

5.

ПРИМЕНЕНИЕ ТРИГОНОМЕТРИИ
1. Астрономия: измерение расстояний между звездами.
2. География: расчёт расстояний на поверхности Земли.
3. Архитектура: проектирование зданий и конструкций.

6.

ПРИМЕНЕНИЕ ТРИГОНОМЕТРИИ В
ГЕОМЕТРИИ И ФИЗИКЕ
• Тригонометрические вычисления применяются практически во всех
областях геометрии, физики и инженерного дела. Например,
большое значение имеет техника триангуляции, позволяющая
измерять расстояния до недалёких звёзд в астрономии, между
ориентирами в географии, контролировать системы навигации
спутников.

7.

Р Е А Л Ь Н Ы Е П Р И М Е Р Ы И С П ОЛ ЬЗО ВА Н И Я
ТРИГОНОМЕТРИИ
• Тригонометрия или тригонометрические функции используются в астрономии (особенно
для расчётов положения небесных объектов), когда требуется сферическая
тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в
анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в
биологии, в медицинской визуализации ,например, компьютерной томографии и
ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в
океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в
фонетике, в экономике, в электротехнике, в машиностроении, в гражданском
строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке
игр и многих других областях.

8.

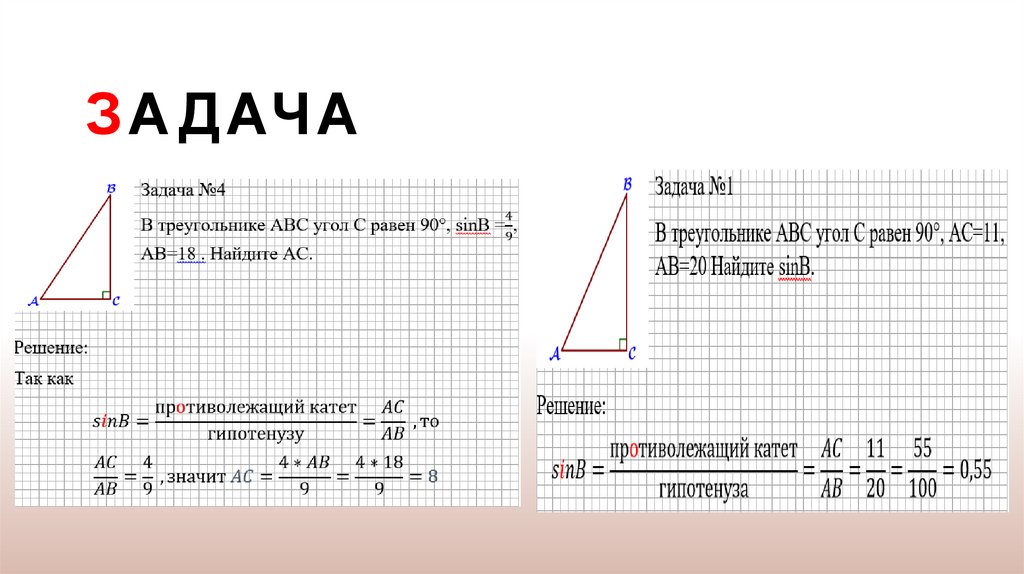
З А Д АЧ А

9.

ЗАКЛЮЧЕНИЕ
• Тригонометрия — важная наука, используемая в жизни,
технике и архитектуре.
• Её изучение помогает лучше понимать окружающий мир.
• Спасибо за внимание