Моделирование на графах

1.

МОДЕЛИРОВАНИЕ
НА ГРАФАХ
ИНФОРМАЦИОННОЕ МОДЕЛИРОВАНИЕ

2.

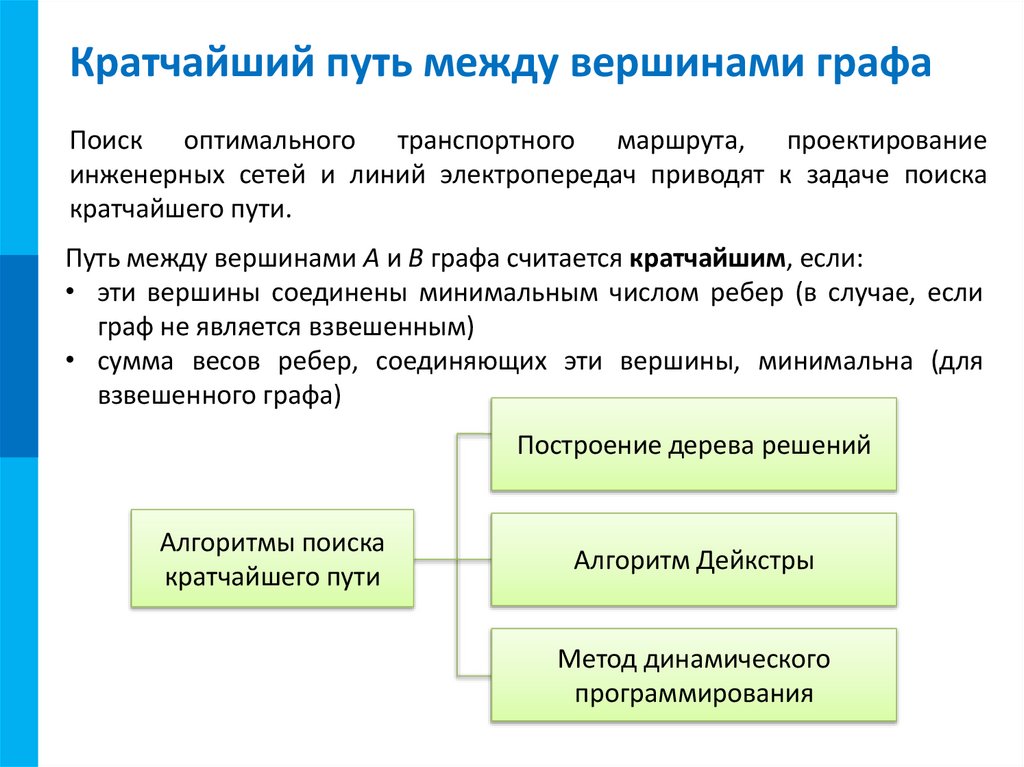
МК
Кратчайший путь между вершинами графа
Поиск оптимального транспортного маршрута, проектирование
инженерных сетей и линий электропередач приводят к задаче поиска
кратчайшего пути.
Путь между вершинами А и В графа считается кратчайшим, если:
• эти вершины соединены минимальным числом ребер (в случае, если
граф не является взвешенным)
• сумма весов ребер, соединяющих эти вершины, минимальна (для
взвешенного графа)
Построение дерева решений
Алгоритмы поиска
кратчайшего пути
Алгоритм Дейкстры
Метод динамического
программирования

3.

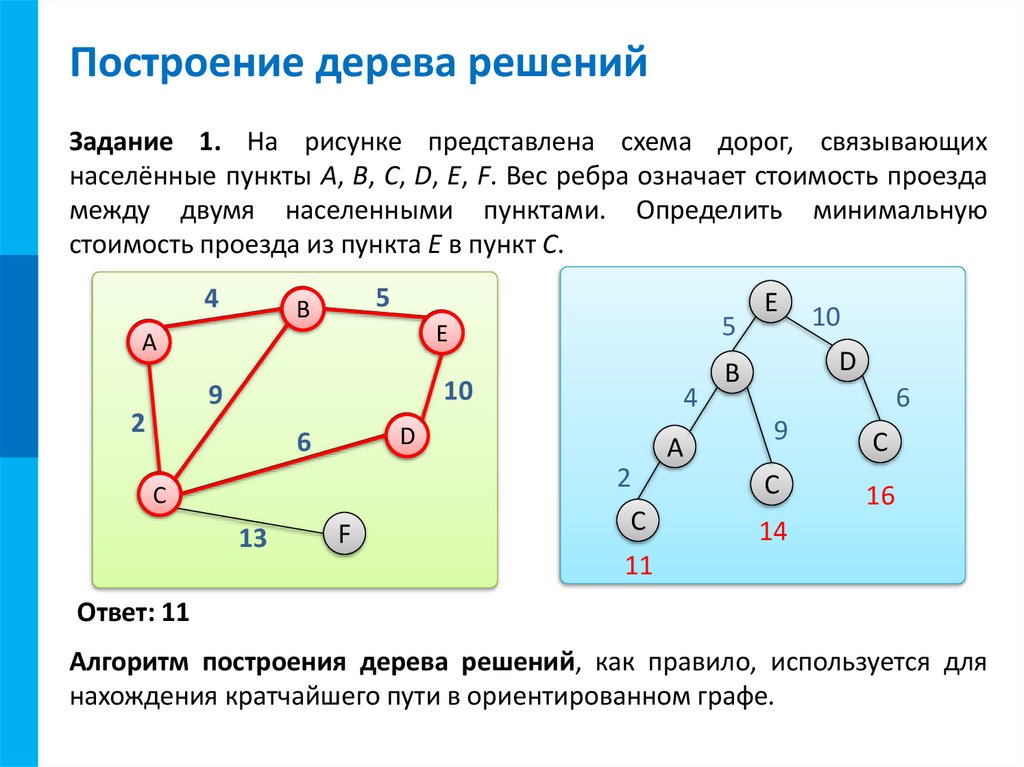
МК
Построение дерева решений
Задание 1. На рисунке представлена схема дорог, связывающих
населённые пункты A, B, C, D, E, F. Вес ребра означает стоимость проезда
между двумя населенными пунктами. Определить минимальную
стоимость проезда из пункта E в пункт C.
4
5
B
A
10
9
2
5
E
C
F
10
D
B
6
9
С
2
C
C
16
14
D
6
13
4
E
A
11
Ответ: 11
Алгоритм построения дерева решений, как правило, используется для
нахождения кратчайшего пути в ориентированном графе.

4.

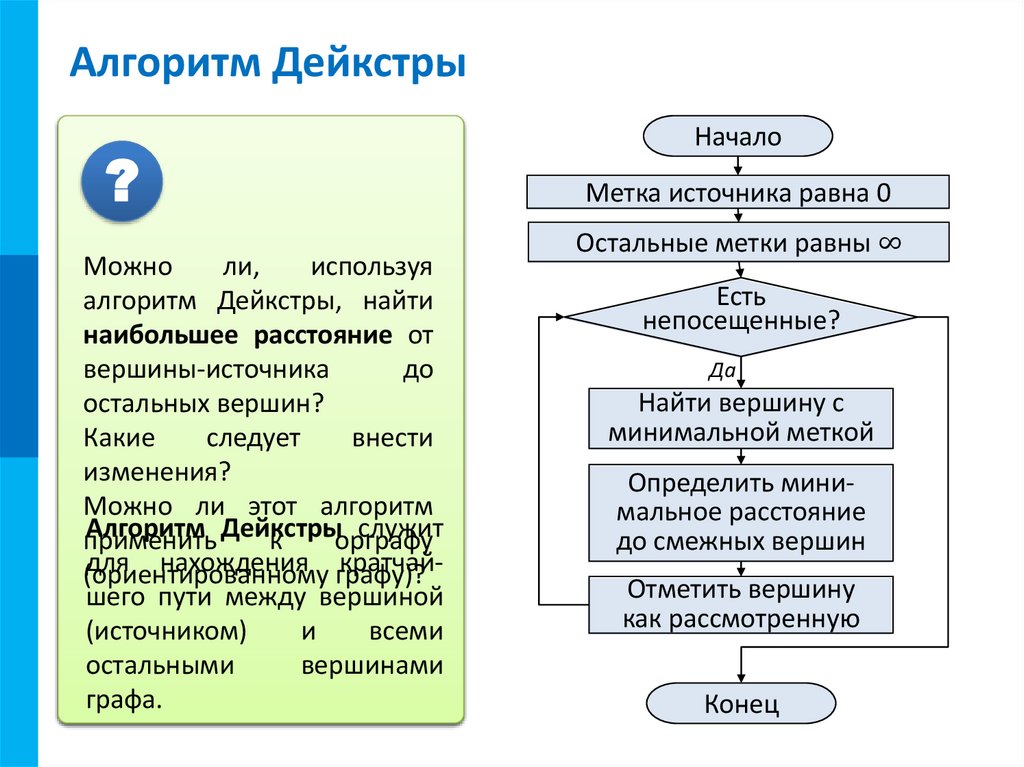
МК
Алгоритм Дейкстры
Задание 2. Определить
минимальное расстояние от
вершины A до F.
?
∞
2
Можно B ли,
∞
7
E
5 используя
2Дейкстры, найти
алгоритм
9
A 0
10от
наибольшее
расстояние
13
вершины-источника
до
2
∞ C
13
11
остальных
вершин? D 17
∞
15
Какие 4 следует
внести
6
изменения? F ∞
15
Можно ли этот алгоритм
Алгоритм
Дейкстры
служит
применить
к
орграфу
- рассматриваемая
вершина
для нахождения графу)?
кратчай(ориентированному
вершина
шего- рассмотренная
пути между вершиной
Ответ: 15
(источником)
и
всеми
- непосещённая вершина
остальными
вершинами
графа.
Начало
Метка источника равна 0
Остальные метки равны ∞
Есть
непосещенные?
Да
Найти вершину с
минимальной меткой
Определить минимальное расстояние
до смежных вершин
Отметить вершину
как рассмотренную
Конец

5.

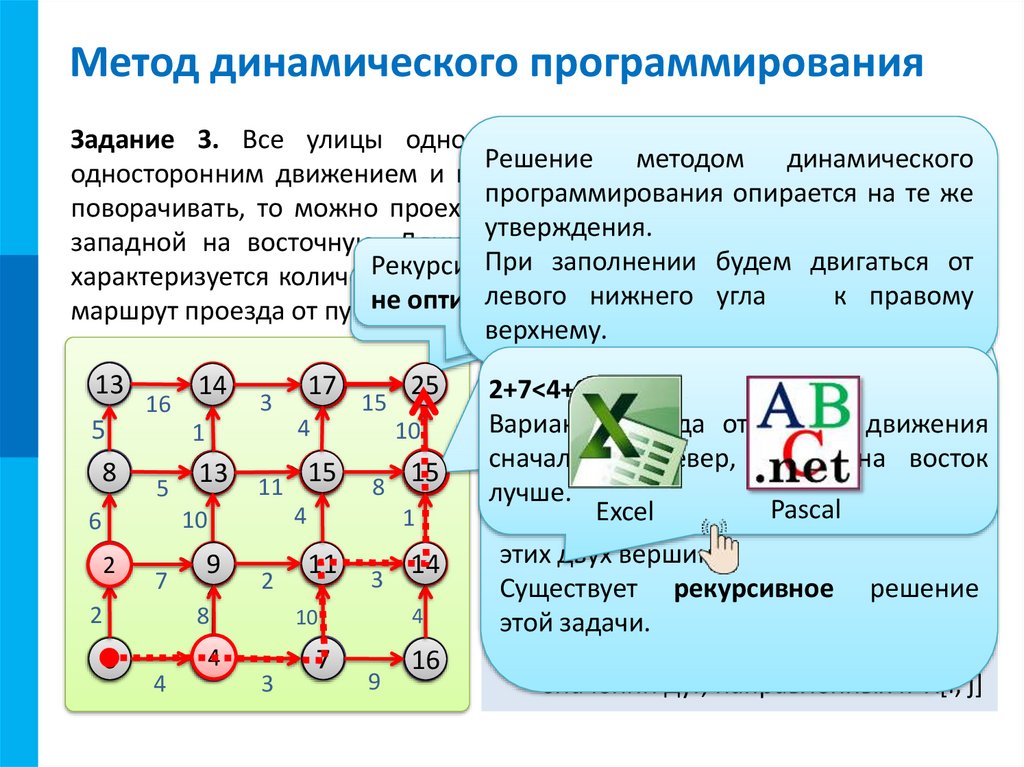
МК
Метод динамического программирования
Задание 3. Все улицы одного из кварталов города N прямые с
Решение методом динамического
односторонним движением и пересекаются под прямым углом. Если не
программирования опирается на те же
поворачивать, то можно проехать с южной окраины на северную или с
утверждения.
западной на восточную. Длины переулков равны, но каждый участок
При заполнении
будем задачи
двигаться от
Рекурсивное
решение
этой
характеризуется количеством
ям на дороге.
Необходимо
выбрать лучший
левогопонижнего
угла
к правому
не определить
оптимально
скорости
выполнения.
Как
движения?
маршрут проезда от пункта
A в пункт B. маршрут
верхнему.
13
5
8
16
14
3
1
5
13
2
7
9
4
8
4
2
11
8
10
A
0
4
7
3
15
1
2
4
15
25
B
10
15
11
10
6
17
3
14
4
9
16
Попасть в вершину B можно только из
2+7<4+8
значение
стартовой
(зеленой)
двух
вершин.
Значение
лучшего
Вариант
проезда
отравно
начала
движения
вершины
A[1, 1]
нулю
вариантаназависит
тольконаотвосток
веса
сначала
север, непотом
ребер,
но и – от сумма
того, сзначений
каким
лучше.
значение
Pascal
Excel
«результатом»
можно
добраться до
предшествующих
участков
этих двух вершин.
значение врекурсивное
вершине X[i, решение
j] равно
Существует
из значений вершин
этойменьшему
задачи.
X[i-1, j] и X[i, j-1] с учетом весовых
значений дуг, направленных к X[i, j]