Динамические структуры данных. Графы

1. Динамические структуры данных

Графы

2.

2
Определения
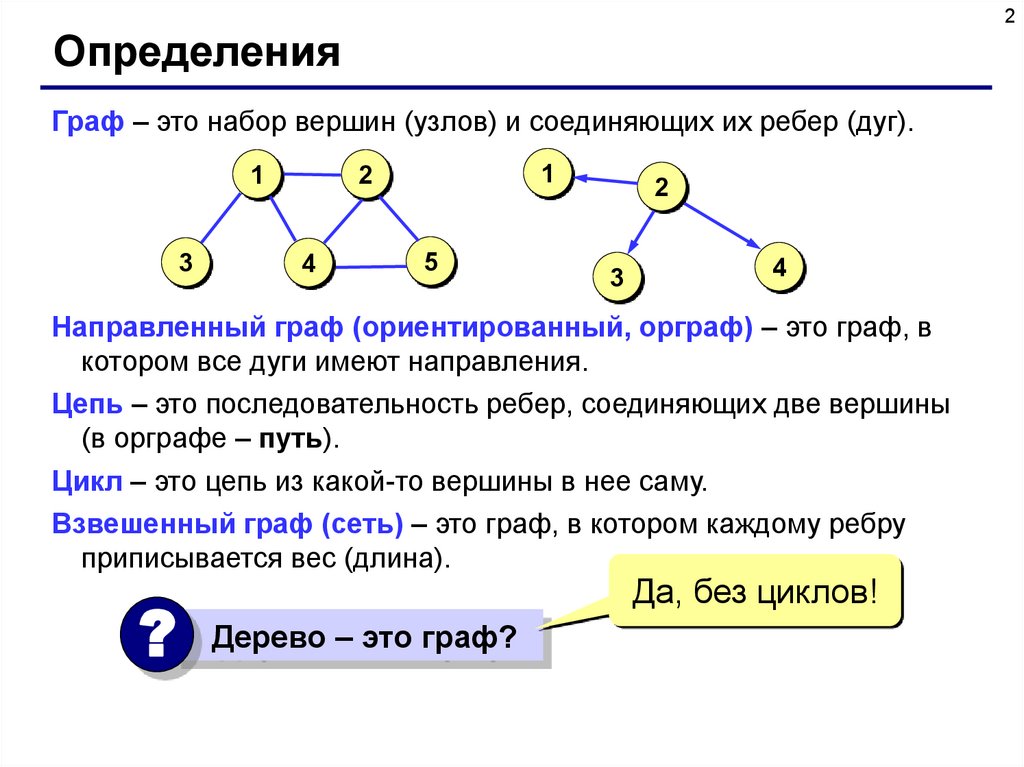
Граф – это набор вершин (узлов) и соединяющих их ребер (дуг).
1
3
1
2
4
5
2
3
4
Направленный граф (ориентированный, орграф) – это граф, в
котором все дуги имеют направления.
Цепь – это последовательность ребер, соединяющих две вершины
(в орграфе – путь).
Цикл – это цепь из какой-то вершины в нее саму.
Взвешенный граф (сеть) – это граф, в котором каждому ребру
приписывается вес (длина).
? Дерево – это граф?
Да, без циклов!

3.

3
Определения
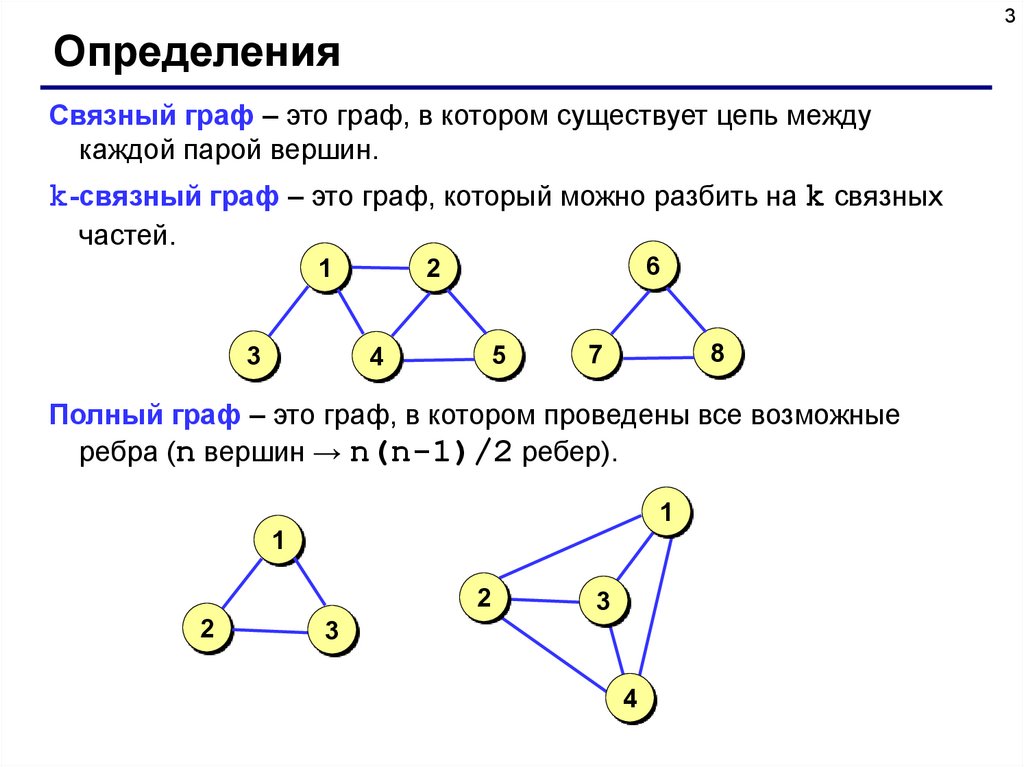
Связный граф – это граф, в котором существует цепь между
каждой парой вершин.
k-cвязный граф – это граф, который можно разбить на k связных
частей.
1
3
6
2
5
4
8
7
Полный граф – это граф, в котором проведены все возможные
ребра (n вершин → n(n-1)/2 ребер).
1
1
2
2
3
3
4

4.

4
Описание графа
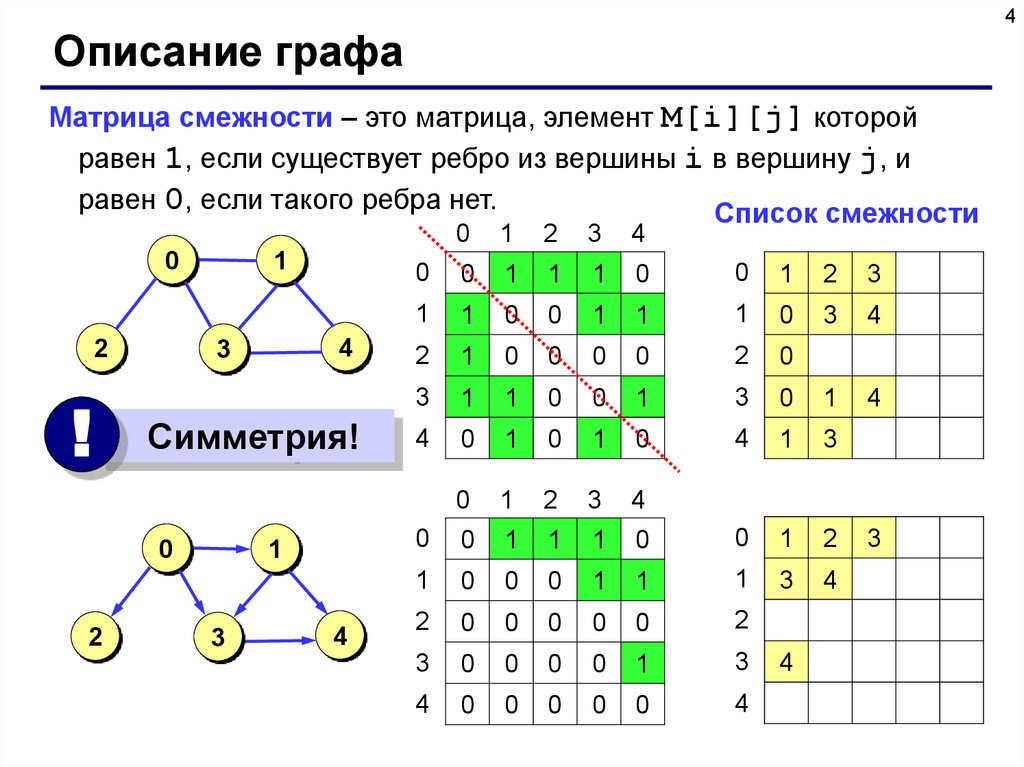
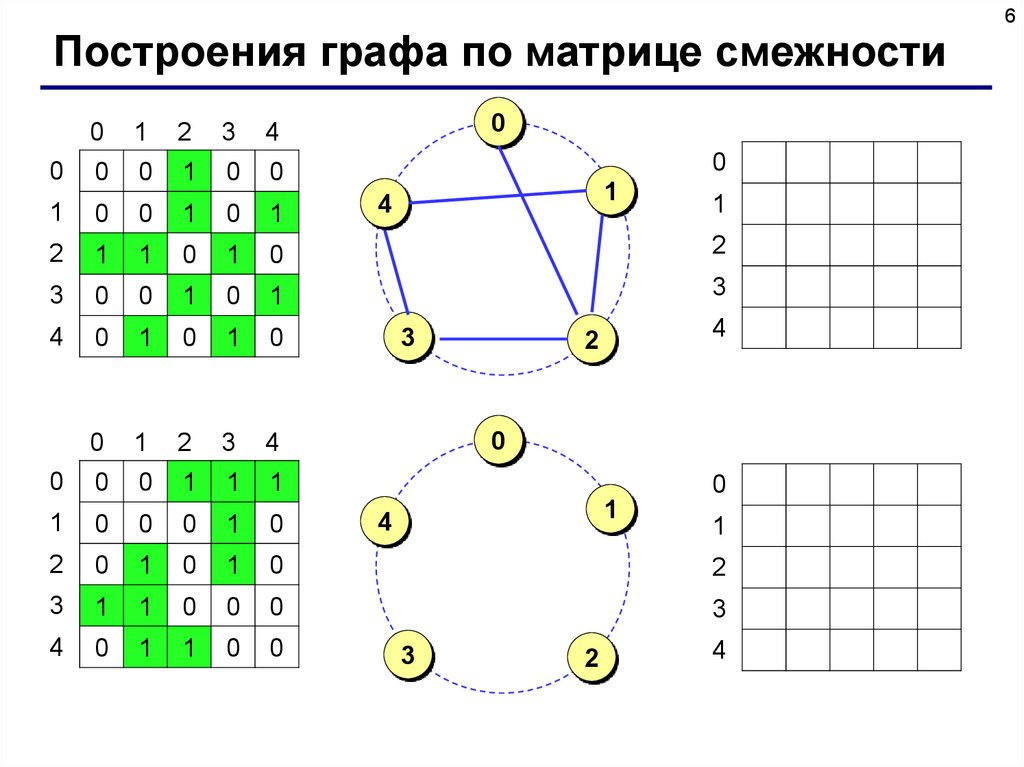
Матрица смежности – это матрица, элемент M[i][j] которой
равен 1, если существует ребро из вершины i в вершину j, и
равен 0, если такого ребра нет.
Список смежности
0
2
!
1
Симметрия!
0
2
4
3
1
3
4
0
1
2
3
4
0
0
1
1
1
0
0
1
2
3
1
1
0
0
1
1
1
0
3
4
2
1
0
0
0
0
2
0
3
1
1
0
0
1
3
0
1
4
4
0
1
0
1
0
4
1
3
0
1
2
3
4
0
0
1
1
1
0
0
1
2
1
0
0
0
1
1
1
3
4
2
0
0
0
0
0
2
3
0
0
0
0
1
3
4
0
0
0
0
0
4
4
3

5.

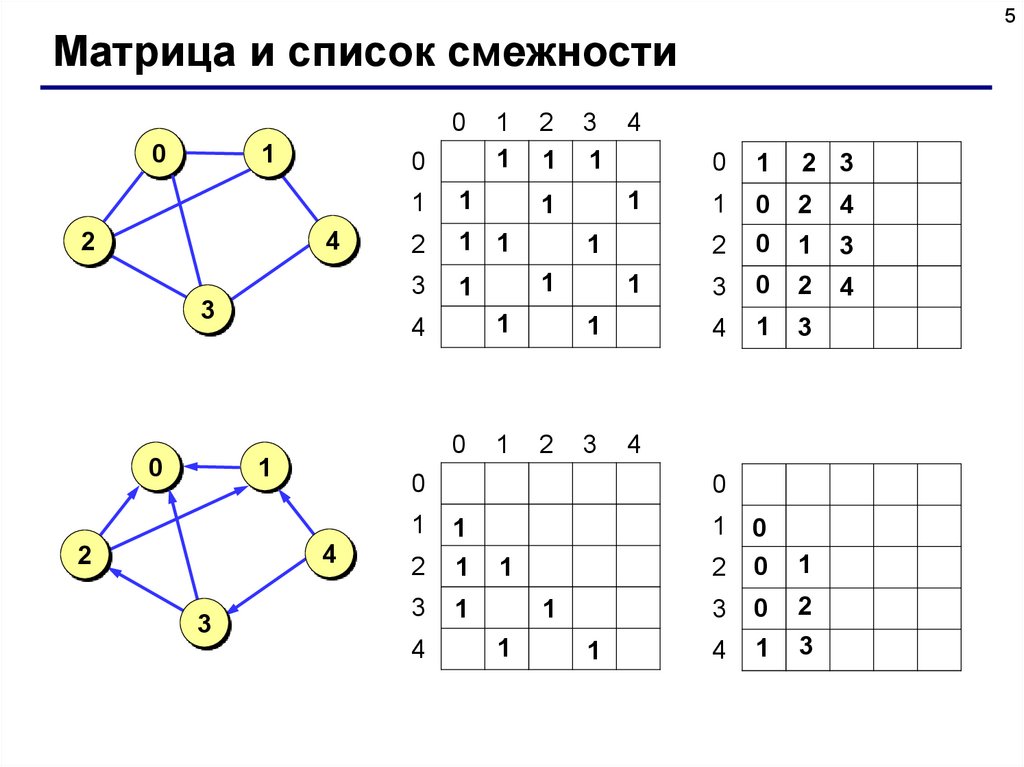
5
Матрица и список смежности
0
0
1
0
4
2
3
0
3
1
2
1 1
3
1
2
1
3 4
1
0
1
2 3
1
1
1
0
2
4
2
0
1
3
3
0
2
4
4
1
3
1
1
1
0
1
1
1
2
3
0
4
2
1
4
1
1
1
0
1
1
2
1
3
1
4
4
1
1
1
1
1
0
2
0
1
3
0
2
4
1
3

6.

6
Построения графа по матрице смежности
0
0
1
2
3
4
0
0
1
0
0
0
0
1
4
1
1
0
0
1
0
1
2
1
1
0
1
0
2
3
0
0
1
0
1
3
4
0
1
0
1
0
0
1
2
3
4
0
0
0
1
1
1
1
0
0
0
1
0
2
0
1
0
1
0
2
3
1
1
0
0
0
3
4
0
1
1
0
0
3
4
2
0
0
1
4
3
2
1
4

7.

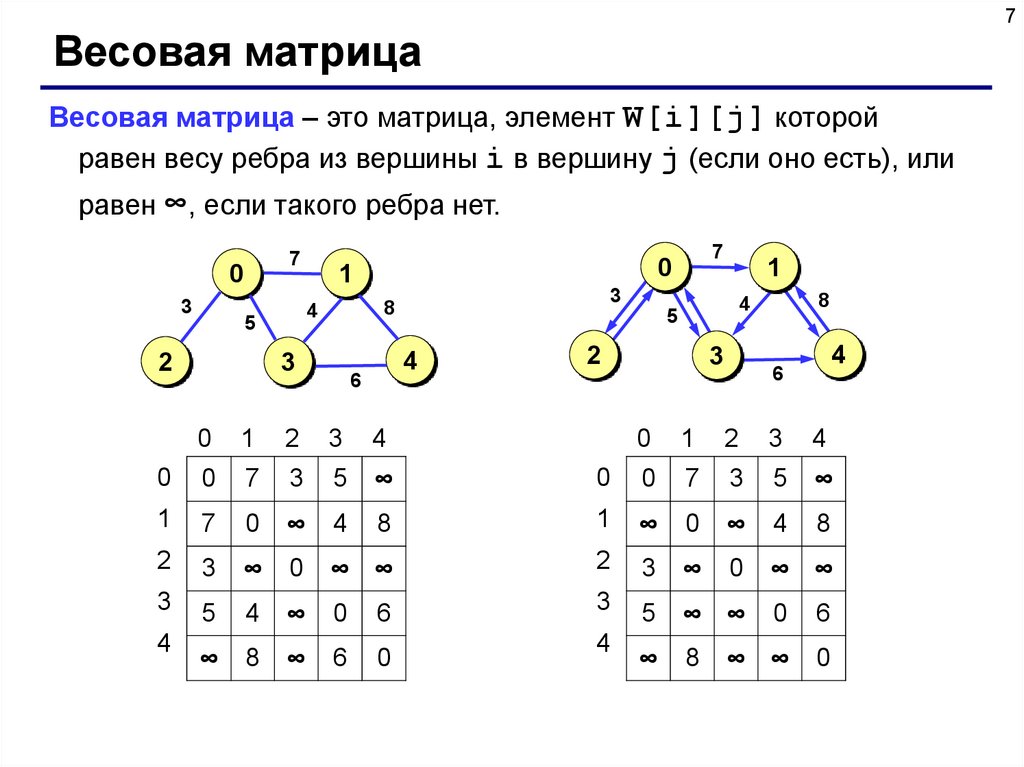
7
Весовая матрица
Весовая матрица – это матрица, элемент W[i][j] которой
равен весу ребра из вершины i в вершину j (если оно есть), или
равен ∞, если такого ребра нет.
7
0
3
5
2
1
3
0
1
2
3
4
0
0
7
3
5
∞
1
7
0
∞ 4
2
8
4
5
4
6
1
3
8
4
7
0
2
3
4
6
0
1
2
3
4
0
0
7
3
5
∞
8
1
∞ 0 ∞ 4
8
3
∞ 0 ∞ ∞
2
3
∞ 0 ∞ ∞
3
5
4
∞ 0
6
3
5
∞ ∞ 0
4
∞ 8 ∞ 6
0
4
∞ 8 ∞ ∞ 0
6

8.

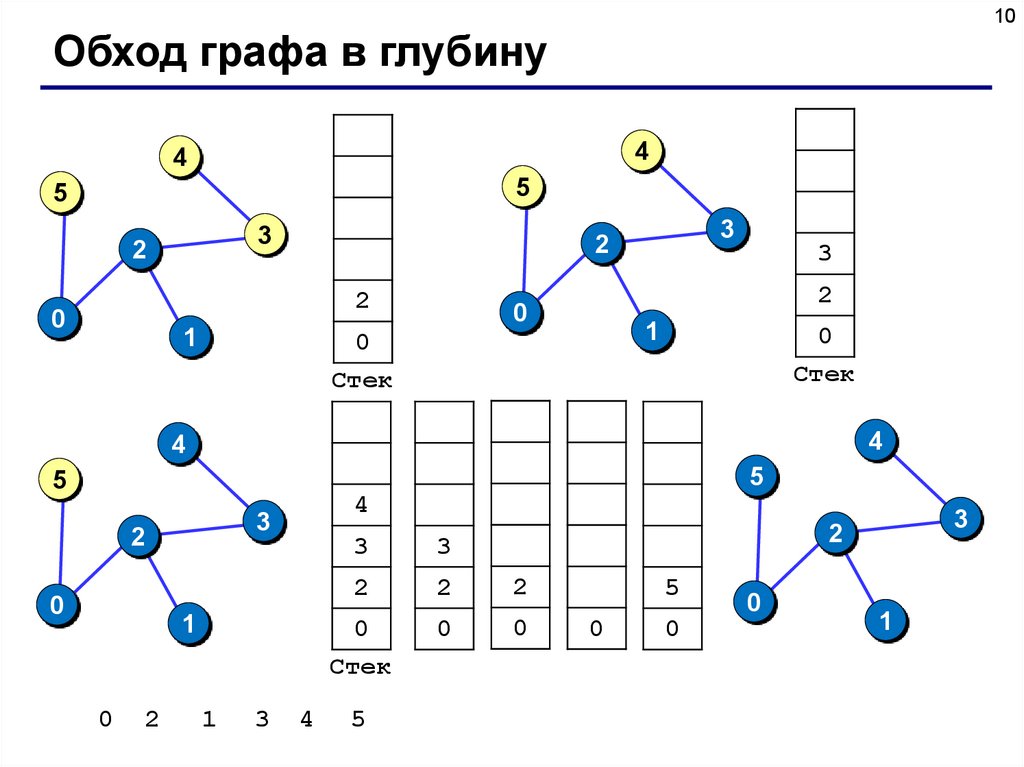
8
Обход графа в глубину
Используется стек.
1) Посетить вершину p и поместить ее в пустой стек.
2) Если стек не пуст, перейти к шагу 3, иначе перейти к
шагу 7.
3) Если у вершины р на верхушке стека есть не
посещённая смежная вершина q, перейти к шагу 4,
иначе, перейти к шагу 5.
4) Посетить вершину q и поместить ее в стек.
5) Извлечь вершину р с верхушки стека.
6) Перейти к шагу 2.
7) Конец алгоритма.

9.

9
Обход графа в глубину
4
4
5
5
3
2
0
1
0
Стек
2
0
1
5
5
3
2
1
1
0
Стек
3
2
1
2
0
2
0
Стек
4
4
0
3
2
0
2
1
0
Стек

10.

10
Обход графа в глубину
4
4
5
5
3
2
2
0
3
2
1
3
2
0
1
0
Стек
0
Стек
4
4
5
5
2
0
4
3
1
0
2
1
3
4
3
3
2
2
2
0
Стек
0
0
5
3
2
5
0
0
0
1

11.

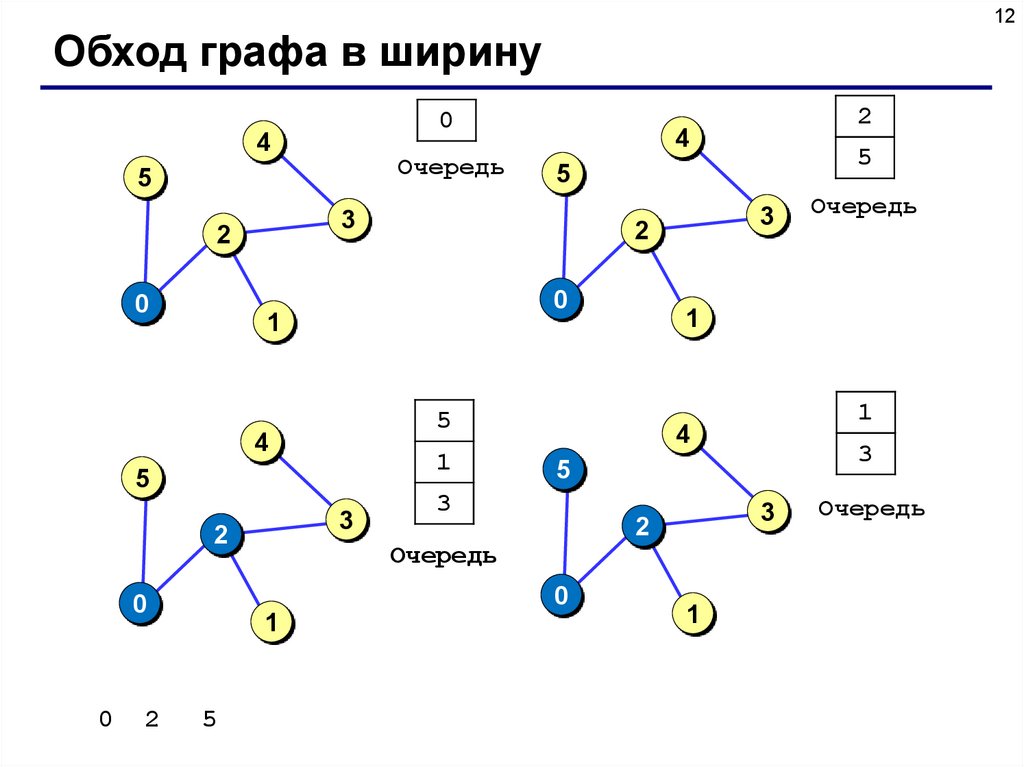
11
Обход графа в ширину
Используется очередь.
1) Посетить вершину p и поместить ее в пустую очередь.
2) Если очередь не пуста, перейти к шагу 3, иначе
перейти к шагу 6.
3) Извлечь вершину р из очереди.
4) Если р еще не посещалась, поместить в очередь все
вершины, смежные с р.
5) Перейти к шагу 2.
6) Конец алгоритма.

12.

12
Обход графа в ширину
0
4
Очередь
5
0
1
3
2
2
5
3
5
3
3
2
Очередь
1
1
4
0
0
Очередь
1
5
5
3
2
1
5
5
0
4
0
4
3
2
2
1
Очередь

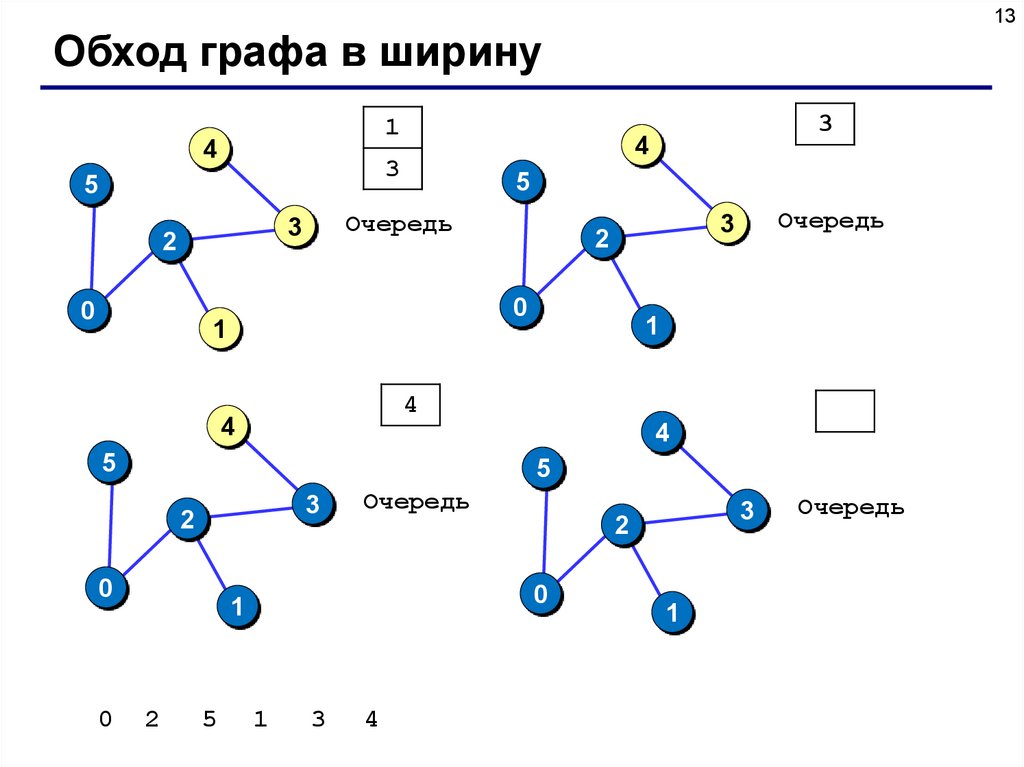
13.

13
Обход графа в ширину
1
4
2
5
Очередь
3
0
4
3
5
Очередь
3
2
0
1
1
4
4
4
5
5
3
2
0
0
3
Очередь
0
1
2
5
1
3
3
2
4
1
Очередь

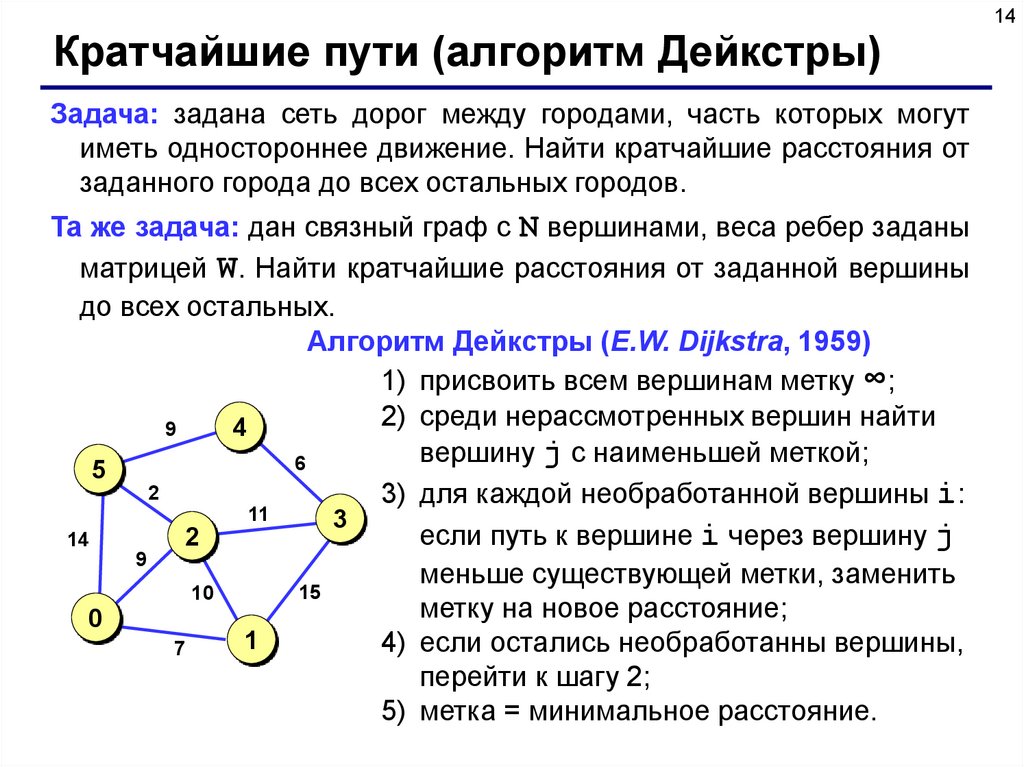
14.

14
Кратчайшие пути (алгоритм Дейкстры)
Задача: задана сеть дорог между городами, часть которых могут
иметь одностороннее движение. Найти кратчайшие расстояния от
заданного города до всех остальных городов.
Та же задача: дан связный граф с N вершинами, веса ребер заданы
матрицей W. Найти кратчайшие расстояния от заданной вершины
до всех остальных.
Алгоритм Дейкстры (E.W. Dijkstra, 1959)
1) присвоить всем вершинам метку ∞;
2) среди нерассмотренных вершин найти
9
4
вершину j с наименьшей меткой;
6
5
2
3) для каждой необработанной вершины i:
11
3
если путь к вершине i через вершину j
2
14
9
меньше существующей метки, заменить
15
10
метку на новое расстояние;
0
1
4) если остались необработанны вершины,
7
перейти к шагу 2;
5) метка = минимальное расстояние.

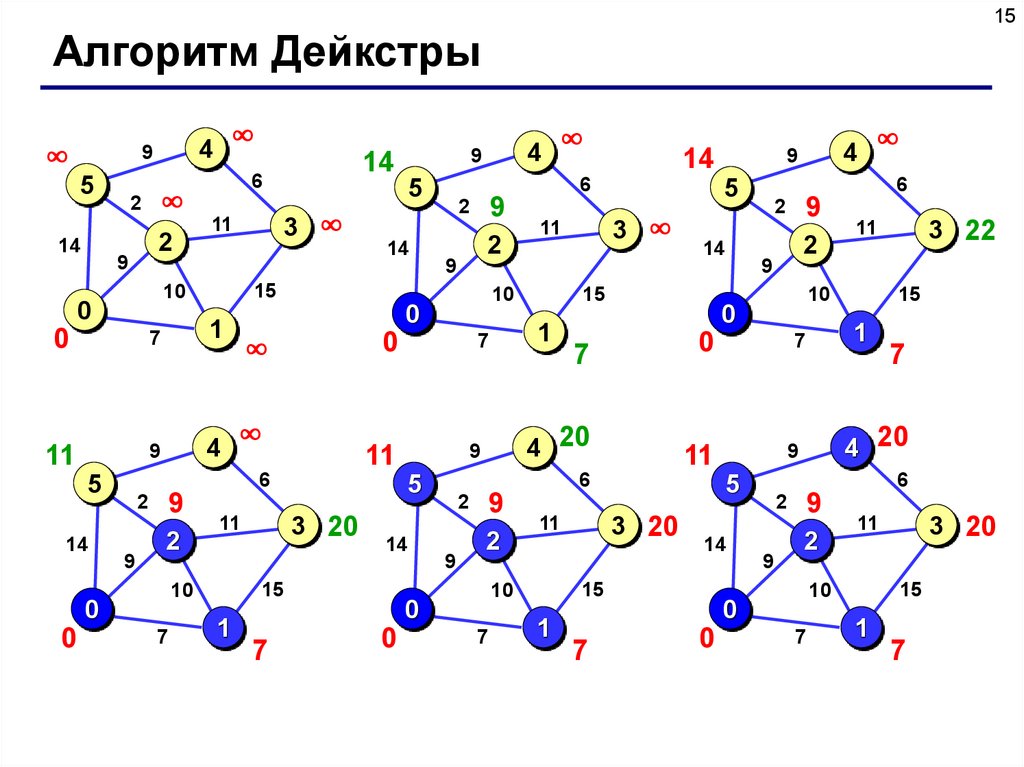
15.

15
Алгоритм Дейкстры
∞
5
14
2
∞
2
9
∞
4
9
11
0
7
11
9
4
2
9
9
2
∞
∞
7
9
7
1
11
9
14
7
3
∞
2
9
9
2
14
∞
6
9
2
2
9
15
10
0
3 22
11
7
0
7
1
4 20
11
9
4 20
14
15
1
7
2
9
9
2
7
3 20
11
15
10
0
0
7
6
5
3 20
11
10
7
4
9
5
6
0
0
14
15
0
15
1
11
10
5
3 20
11
10
0
2
0
6
5
0
14
9
2
15
1
14
∞
∞
6
5
3
10
0
14
6
4
9
1
7

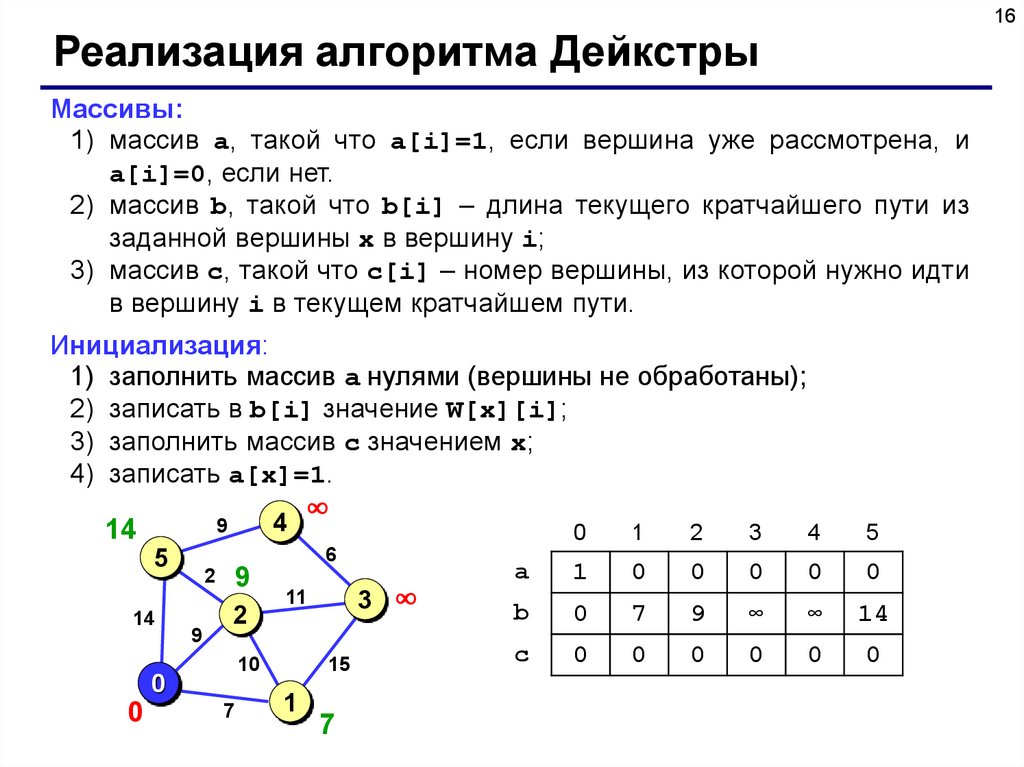
16.

16
Реализация алгоритма Дейкстры
Массивы:
1) массив a, такой что a[i]=1, если вершина уже рассмотрена, и
a[i]=0, если нет.
2) массив b, такой что b[i] – длина текущего кратчайшего пути из
заданной вершины x в вершину i;
3) массив c, такой что c[i] – номер вершины, из которой нужно идти
в вершину i в текущем кратчайшем пути.
Инициализация:
1) заполнить массив a нулями (вершины не обработаны);
2) записать в b[i] значение W[x][i];
3) заполнить массив c значением x;
4) записать a[x]=1.
4
9
14
6
5
14
2
9
9
2
11
7
3
15
10
0
0
∞
1
7
∞
0
1
2
3
4
5
a
1
0
0
0
0
0
b
0
7
9
∞
∞
14
c
0
0
0
0
0
0

17.

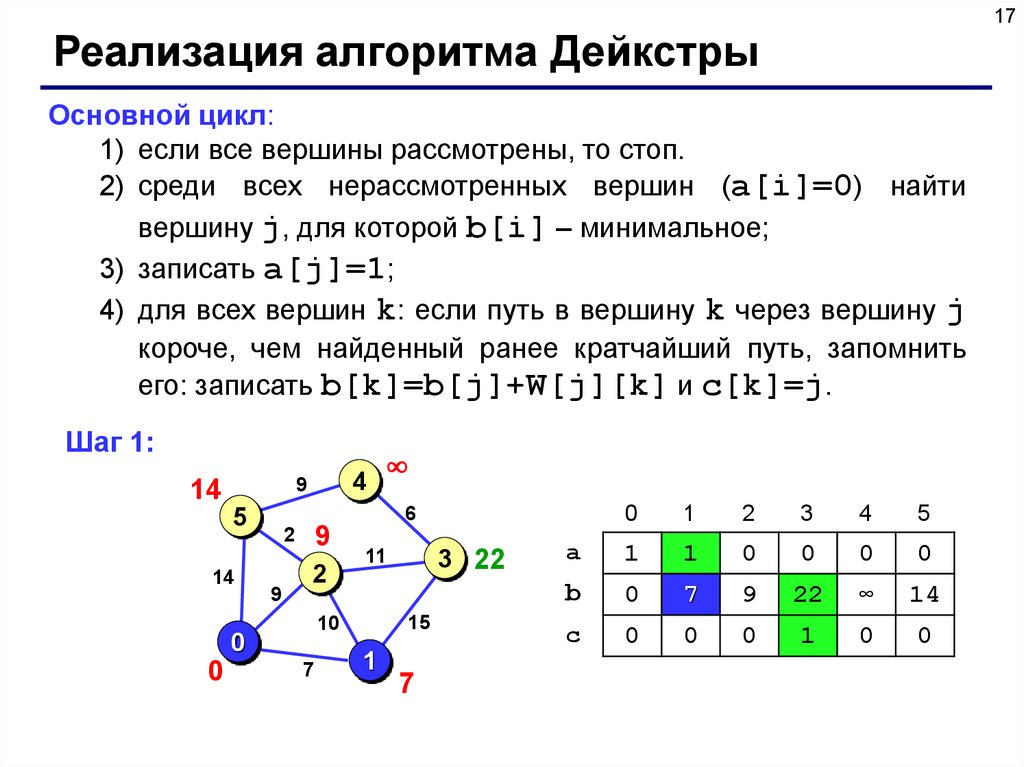
17
Реализация алгоритма Дейкстры
Основной цикл:
1) если все вершины рассмотрены, то стоп.
2) среди всех нерассмотренных вершин (a[i]=0) найти
вершину j, для которой b[i] – минимальное;
3) записать a[j]=1;
4) для всех вершин k: если путь в вершину k через вершину j
короче, чем найденный ранее кратчайший путь, запомнить
его: записать b[k]=b[j]+W[j][k] и c[k]=j.
Шаг 1:
4
9
14
2
9
9
2
7
3 22
11
15
10
0
0
0
1
2
3
4
5
a
1
1
0
0
0
0
b
0
7
9
22
∞
14
c
0
0
0
1
0
0
6
5
14
∞
1
7

18.

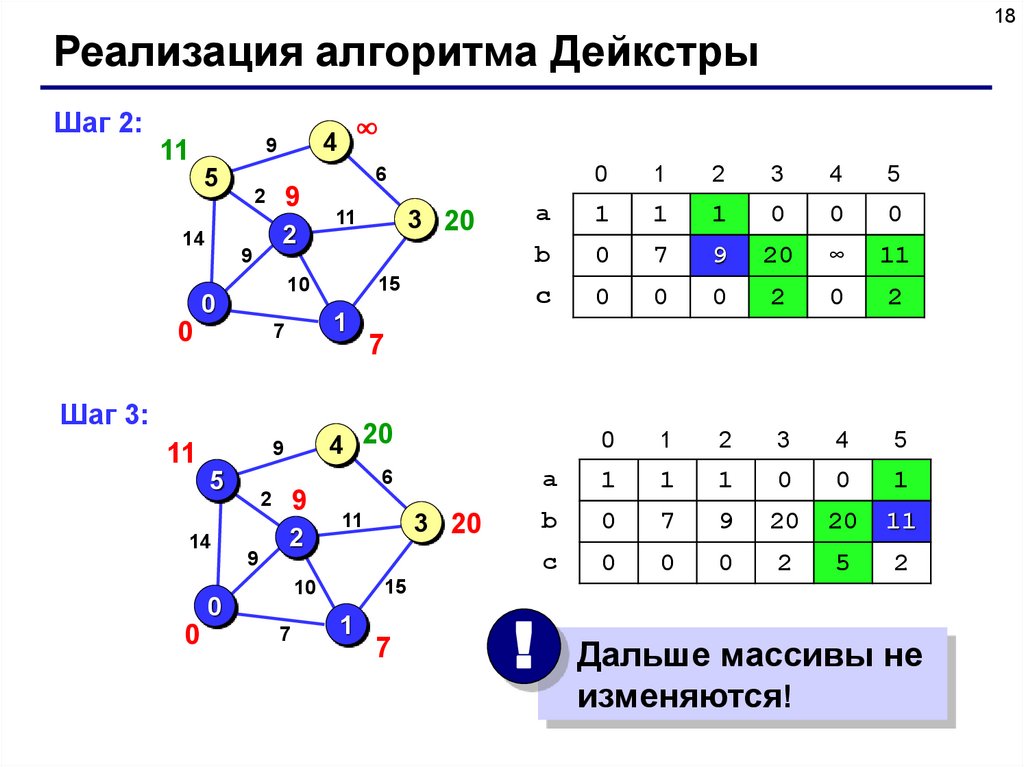
18
Реализация алгоритма Дейкстры
Шаг 2:
11
9
2
2
9
3 20
11
15
10
0
0
7
1
11
9
4 20
Шаг 3:
2
9
9
2
7
3 20
11
2
3
4
5
a
1
1
1
0
0
0
b
0
7
9
20
∞
11
c
0
0
0
2
0
2
0
1
2
3
4
5
a
1
1
1
0
0
1
b
0
7
9
20
20
11
c
0
0
0
2
5
2
15
10
0
0
1
7
6
5
14
0
6
5
14
∞
4
9
1
7
! Дальше массивы не
изменяются!

19.

19
Как вывести маршрут?
Результат работа алгоритма Дейкстры:
0
1
2
3
4
5
a
1
1
1
1
1
1
b
0
7
9
20
20
11
c
0
0
0
2
5
2
длины путей
Маршрут из вершины 0 в вершину 4:
4
5
2
0
Вывод маршрута в вершину i (использование массива c):
1) установить z=i;
2) пока c[i]!=x присвоить z=c[z] и вывести z.
Сложность алгоритма Дейкстры:
два вложенных цикла по N шагов
O(N2)

20.

20
Алгоритм Флойда-Уоршелла
Задача: задана сеть дорог между городами, часть которых могут
иметь одностороннее движение. Найти все кратчайшие
расстояния, от каждого города до всех остальных городов.
for ( k = 0; k < N; k ++ )
for ( i = 0; i < N; i ++ )
for ( j = 0; j < N; j ++ )
if ( W[i][j] > W[i][k] + W[k][j] )
W[i][j] = W[i][k] + W[k][j];
W[i][k]
k
W[k][j]
i
j
W[i][j]
Если из вершины i в
вершину j короче ехать
через вершину k, мы едем
через вершину k!
Нет информации о маршруте, только
! кратчайшие
расстояния!

21.

21
Алгоритм Флойда-Уоршелла
Версия с запоминанием маршрута:
for ( i = 0; i < N; i ++ )
i–ая строка строится так
for ( j = 0; j < N; j ++ )
же, как массив c в
c[i][j] = i;
алгоритме Дейкстры
...
for ( k = 0; k < N; k ++ )
for ( i = 0; i < N; i ++ )
for ( j = 0; j < N; j ++ )
if ( W[i][j] > W[i][k] + W[k][j] )
{
W[i][j] = W[i][k] + W[k][j];
c[i][j] = c[k][j];
}
в конце цикла c[i][j] –
предпоследняя вершина в
кратчайшем маршруте из
вершины i в вершину j
Какова сложность
? алгоритма?
O(N3)

22.

22
Остовное дерево графа
Пусть G=(V, E) – связный неориентированный взвешенный граф, где
V-множество вершин, E-множество ребер.
Остовное дерево графа G=(V, E) – это ациклический связный
подграф данного связного неориентированного графа, в который
входят все его вершины.
Минимальное остовное дерево графа G=(V, E) – это его
ациклический связный подграф, в который входят все его вершины,
обладающий минимальным суммарным весом ребер.
Граф может содержать несколько минимальных остовных деревьев.
Пусть G′ — подграф некоторого минимального остовного дерева
графа G=(V, E).
Ребро (u, v)∉G называется безопасным, если при добавлении его
в G′, G′∪{(u,v)} также является подграфом некоторого минимального
остовного дерева графа G.

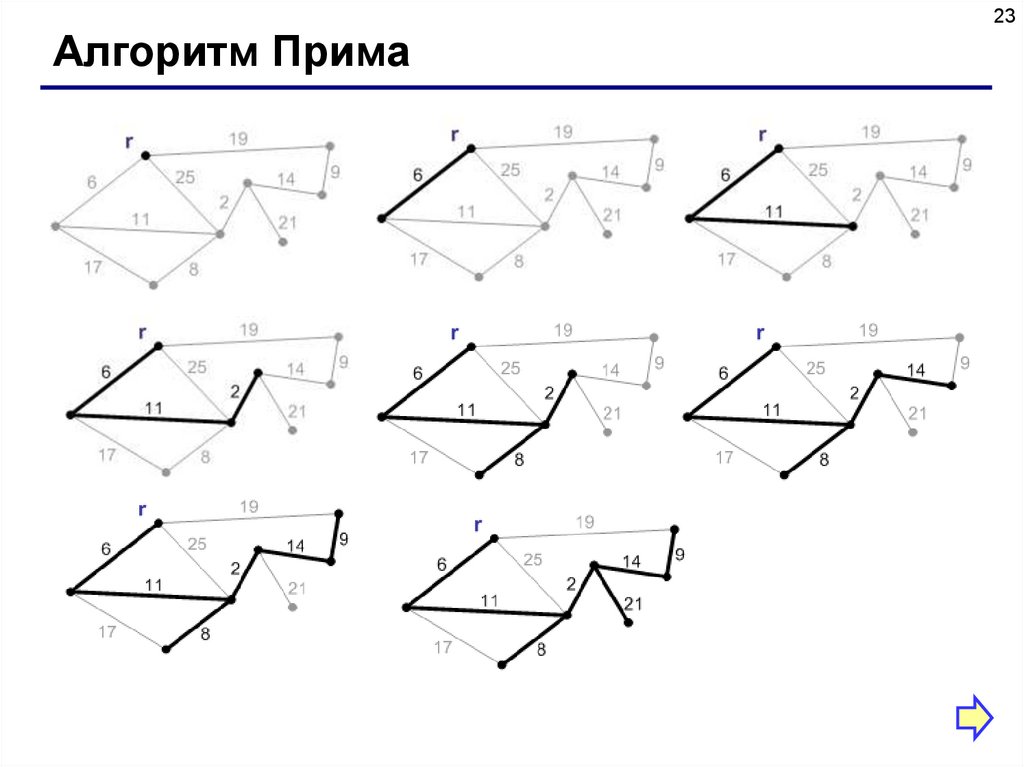
23.

23
Алгоритм Прима

24.

24
Алгоритм Прима
Пусть G – граф, w – весовая матрица, r – корень минимального
остовного дерева графа, Ω – очередь с приоритетом, в которой хранятся
вершины, еще не попавшие в дерево. Приоритет вершины v равен
минимальному весу ребер, соединяющих v с вершинами минимального остова
(key[v]).
MST-PRIM(G,w, r)
1: Ω ← V[G]
2: foreach u ∈ Ω
3: do key[u] ← ∞
4: key[r] ← 0
5: p[r] = NIL
6: while Ω ≠ 0
7: do u ← EXTRACT-MIN(Ω)
8:
foreach v ∈ Adj(u)
9:
do if v ∈ Ω и w(u,v) < key[v] then
10:
p[v] ← u
11:
key[v] ← w(u,v)

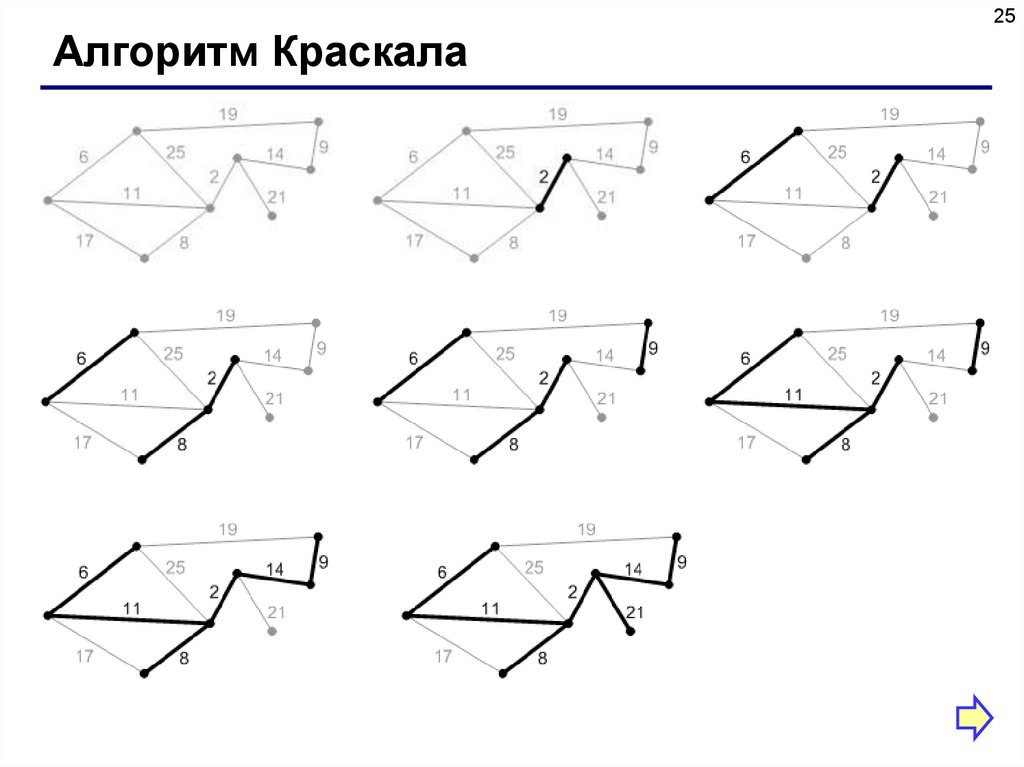
25.

25
Алгоритм Краскала

26.

26
Алгоритм Краскала
MST-KRUSKAL(G,w)
1: A ← 0
2: foreach v ∈ V[G]
3: do Make-Set(v) //создать множество из набора вершин
4: упорядочить ребра по весам
5: for (u,v) ∈ E (в порядке возрастания веса)
6: do if Find-Set(u) ≠ Find-Set(v) then //Find-Set – возв. множ-во с вершиной
7:
A ← A ∪ {(u,v)}
8:
Union(u,v) //объединить множества, содержащие вершины
9: return A

27.

27
Как обнаружить цепи и циклы?
Задача: определить, существует ли цепь длины k из вершины i в
вершину j (или цикл длиной k из вершины i в нее саму).
0
0
1
2
3
0
0
0
1
0
1
1
0
0
0
2
0
1
0
1
3
1
0
0
0
1
M =
2
3
M2[i][j]=1, если M[i][0]=1 и M[0][j]=1 или
M[i][1]=1 и M[1][j]=1 или
M[i][2]=1 и M[2][j]=1 или
M[i][3]=1 и M[3][j]=1
строка i
логическое
умножение
столбец j
логическое
сложение

28.

28
Как обнаружить цепи и циклы?
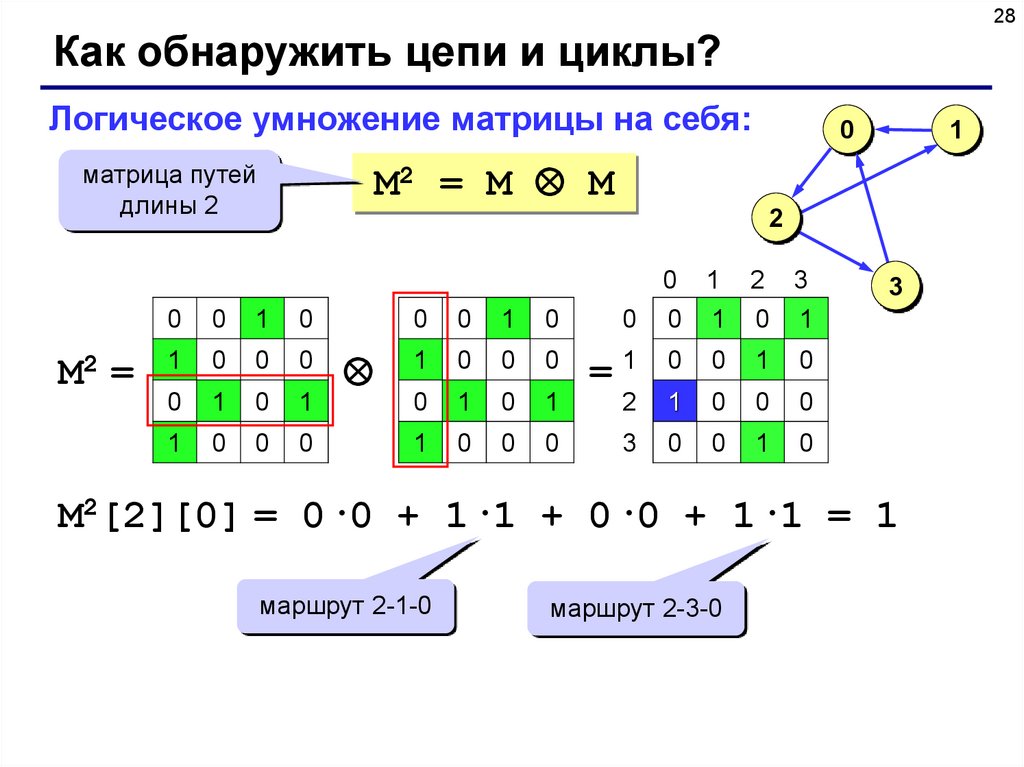
Логическое умножение матрицы на себя:
1
M2 = M M
матрица путей
длины 2
M2 =
0
2
0
0
1
0
1
0
0
0
0
1
0
1
1
0
0
0
0
1
2
3
0
0
1
0
0
0
1
0
1
1
0
0
0
=1
0
0
1
0
0
1
0
1
2
1
0
0
0
1
0
0
0
3
0
0
1
0
3
M2[2][0] = 0·0 + 1·1 + 0·0 + 1·1 = 1
маршрут 2-1-0
маршрут 2-3-0

29.

29
Как обнаружить цепи и циклы?
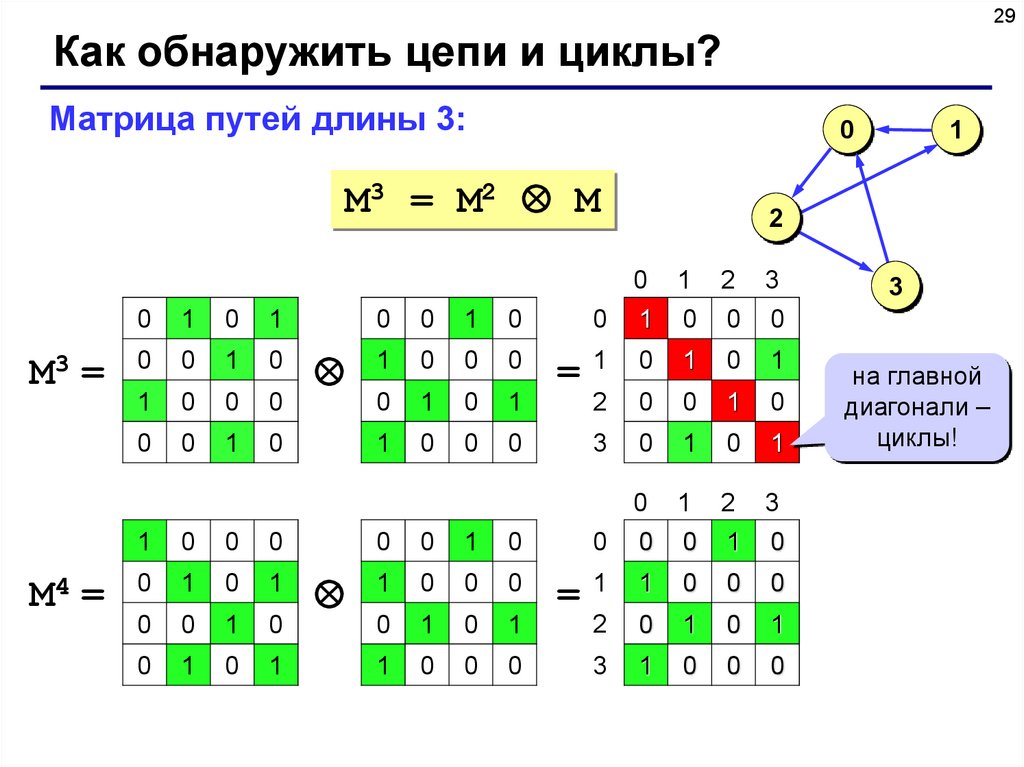
Матрица путей длины 3:
0
M3 = M2 M
M3 =
M4 =
0
1
0
1
0
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
0
1
0
1
0
0
1
0
0
1
0
1
1
2
0
1
2
3
0
0
1
0
0
1
0
0
0
1
0
0
0
=1
0
1
0
1
0
1
0
1
2
0
0
1
0
1
0
0
0
3
0
1
0
1
0
1
2
3
0
0
1
0
0
0
0
1
0
1
0
0
0
=1
1
0
0
0
0
1
0
1
2
0
1
0
1
1
0
0
0
3
1
0
0
0
3
на главной
диагонали –
циклы!