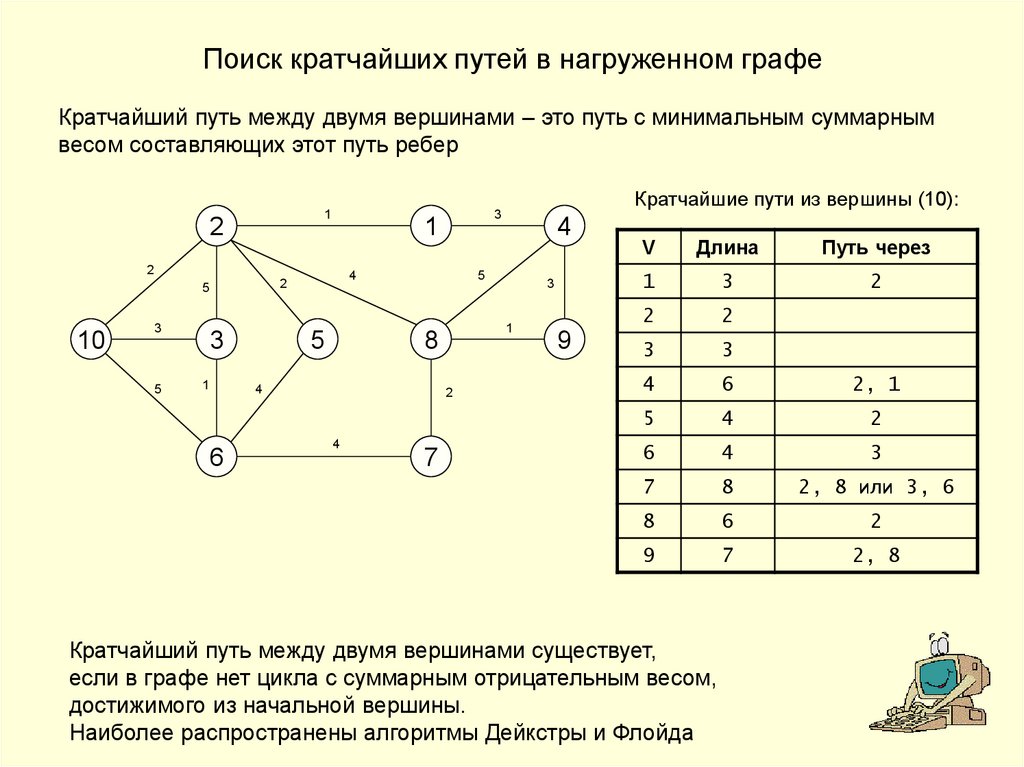
Поиск кратчайших путей в нагруженном графе

1.

2.

3.

Поиск кратчайших путей в нагруженном графе
Кратчайший путь между двумя вершинами – это путь с минимальным суммарным
весом составляющих этот путь ребер
Кратчайшие пути из вершины (10):
1
2
1
2
10
3
5
3
1
6
4
2
5
3
5
5
4
2
7
3
1
8
4
4
9
V
Длина
Путь через
1
3
2
2
2
3
3
4
6
2, 1
5
4
2
6
4
3
7
8
2, 8 или 3, 6
8
6
2
9
7
2, 8
Кратчайший путь между двумя вершинами существует,
если в графе нет цикла с суммарным отрицательным весом,
достижимого из начальной вершины.
Наиболее распространены алгоритмы Дейкстры и Флойда

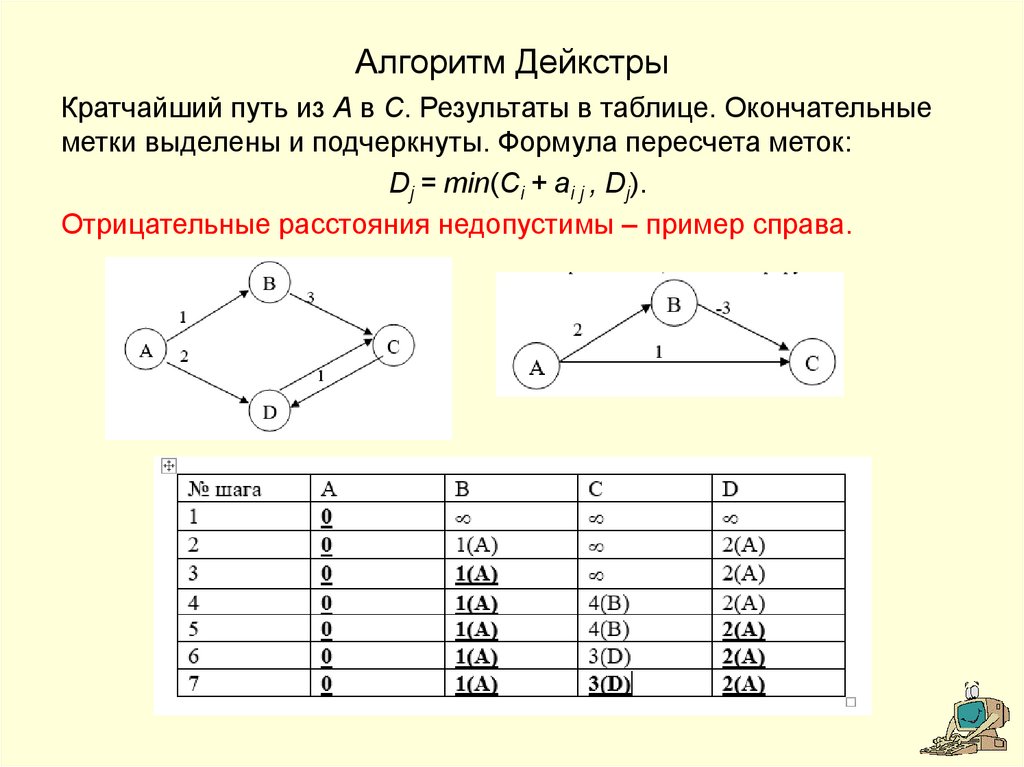
4. Алгоритм Дейкстры

5.

6. Алгоритм Дейкстры

Имеется взвешенный ориентированный граф. В матрице длин А: если нет
дуги i-j, то ai j = , ai i =0. Ищем кратчайший путь из вершины S в вершину T.
Вершинам присваиваются временные и окончательные метки, которые
обозначаются соответственно буквами D и C с индексами вершин.
1.Вершине S присваивается окончательная метка 0, то есть Cs = 0,
временным меткам Dj остальных вершин – значение .
2.Пусть i – номер последней вершины, которой присвоена окончательная
метка Ci. Каждой вершине j, имеющей временную метку Dj, присваивается
новая временная метка по правилу Dj = min(Ci + ai j , Dj). Если значение Dj
меняется, то вместе с ним сохраняется номер предыдущей вершины i.
3.Наименьшая из временных меток объявляется окончательной. Если k –
номер этой вершины, то Ck = Dk.
4.Если новой окончательной метки не появилось, то пути из S в T нет.
5.Если T не получила окончательной метки, то i = k и переход к 2.
6.Конец.

7. Алгоритм Дейкстры

Кратчайший путь из A в C. Результаты в таблице. Окончательные
метки выделены и подчеркнуты. Формула пересчета меток:
Dj = min(Ci + ai j , Dj).
Отрицательные расстояния недопустимы – пример справа.

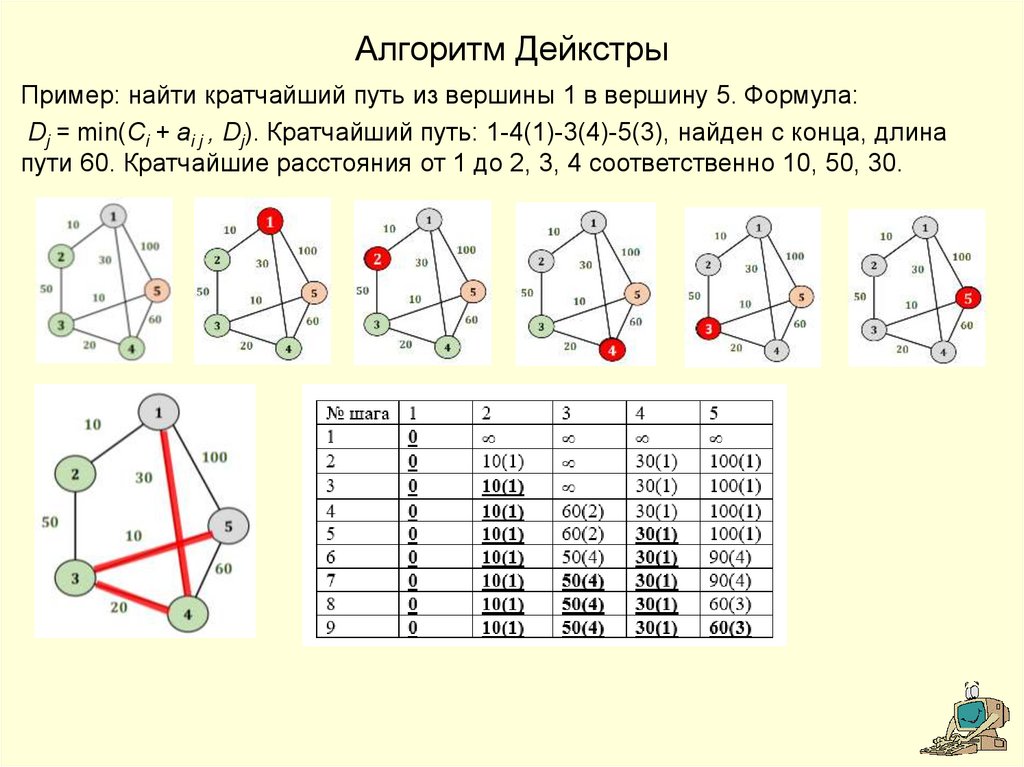
8. Алгоритм Дейкстры

Пример: найти кратчайший путь из вершины 1 в вершину 5. Формула:
Dj = min(Ci + ai j , Dj). Кратчайший путь: 1-4(1)-3(4)-5(3), найден с конца, длина
пути 60. Кратчайшие расстояния от 1 до 2, 3, 4 соответственно 10, 50, 30.

9. Трудоемкость алгоритма Дейкстры

N – число вершин, M – число ребер. В общем случае
M = O(N2).
• Трудоемкость (сложность) простой реализации
алгоритма Дейкстры O(N2).
• Реализация на более сложных структурах данных:
бинарной куче или очереди с приоритетами
O(M log N + N log N).
• В разреженных графах часто M = O(N), поэтому
достигается высокая эффективность. При N = 106
log2N близок к 20.
• Если граф насыщенный, сложные структуры данных
не оправданы.

10. Задача о максимальном грузе

Имеется сеть автомобильных дорог. Каждый участок
дороги имеет максимальную пропускную способность
по весу провозимого груза. Это может объясняться
качеством дорожного полотна, прочностью мостов на
дорожных участках и т. п. Требуется найти маршрут для
доставки максимального груза из заданной начальной
точки в конечную.
Решение: модификация алгоритма Дейкстры.

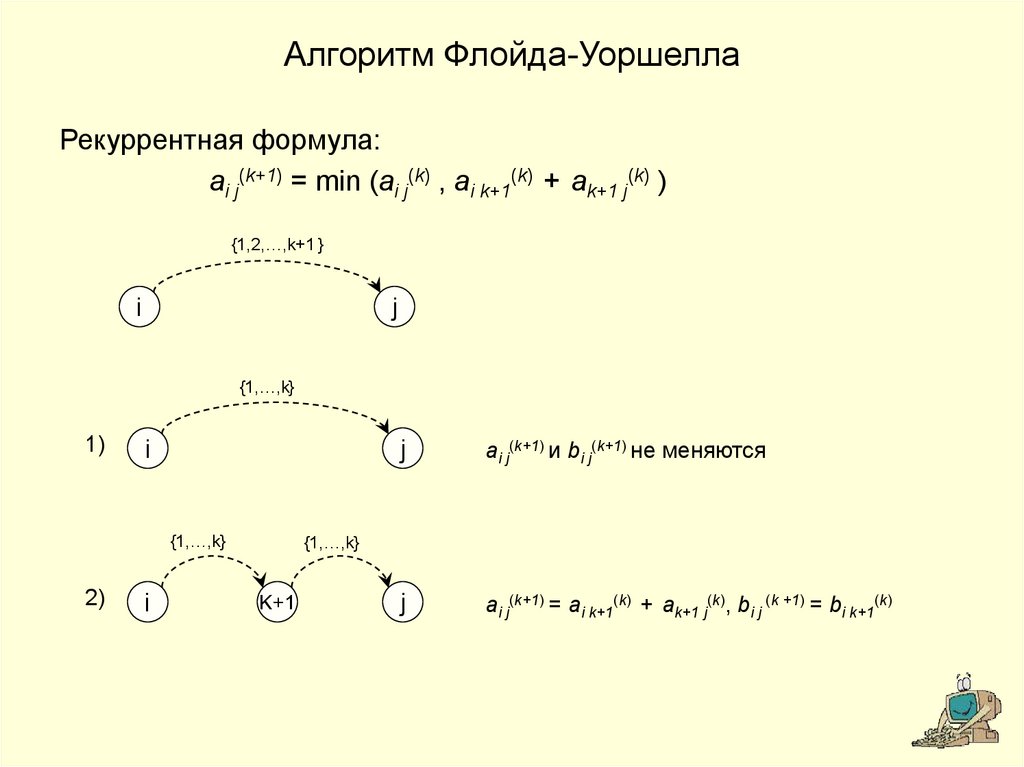
11. Алгоритм Флойда-Уоршелла

Строится последовательность матриц A(0) → A(1) → ... → A(k) → ... → A(n) .
Элемент aij(k) матрицы A(k) равен длине кратчайшего пути из вершины Vi в
вершину Vj, с номерами промежуточных вершин, не превосходящими k.
Рекуррентное соотношение:
aij( k 1) min( aij( k ) , aik( k )1 ak( k )1 j ).
Действительно, на k+1-м шаге либо минимальный путь не меняется, либо
он проходит через вершину Vk+1. Матрица A(n) определет результат.
Для нахождения самих кратчайших путей строится последовательность
матриц B(0) → B(1) → ... → B(k) → ... → B(n) . Элемент bi j(k) матрицы B(k) равен
номеру второй вершины на кратчайшем пути из Vi в Vj с номерами
промежуточных вершин, не превосходящими k, либо 0, если путей нет.
Элемент bi j(k+1) не меняется, если в формуле минимум достигается на
первом значении, и полагается равным bi k+1(k), если минимально второе
выражение, так как в этом случае кратчайший путь проходит через Vk+1.
Если s=bi j(n) дает вторую вершину на кратчайшем пути из Vi в Vj, то t=bs j(n)
третью, w=bt j(n) четвертую и т. д.

12.

Алгоритм Флойда-Уоршелла
Рекуррентная формула:
ai j(k+1) = min (ai j(k) , ai k+1(k) + ak+1 j(k) )
{1,2,…,k+1 }
i
j
{1,…,k}
1)
i
{1,…,k}
2)
i
j
ai j(k+1) и bi j(k+1) не меняются
j
ai j(k+1) = ai k+1(k) + ak+1 j(k), bi j (k +1) = bi k+1(k)
{1,…,k}
K+1

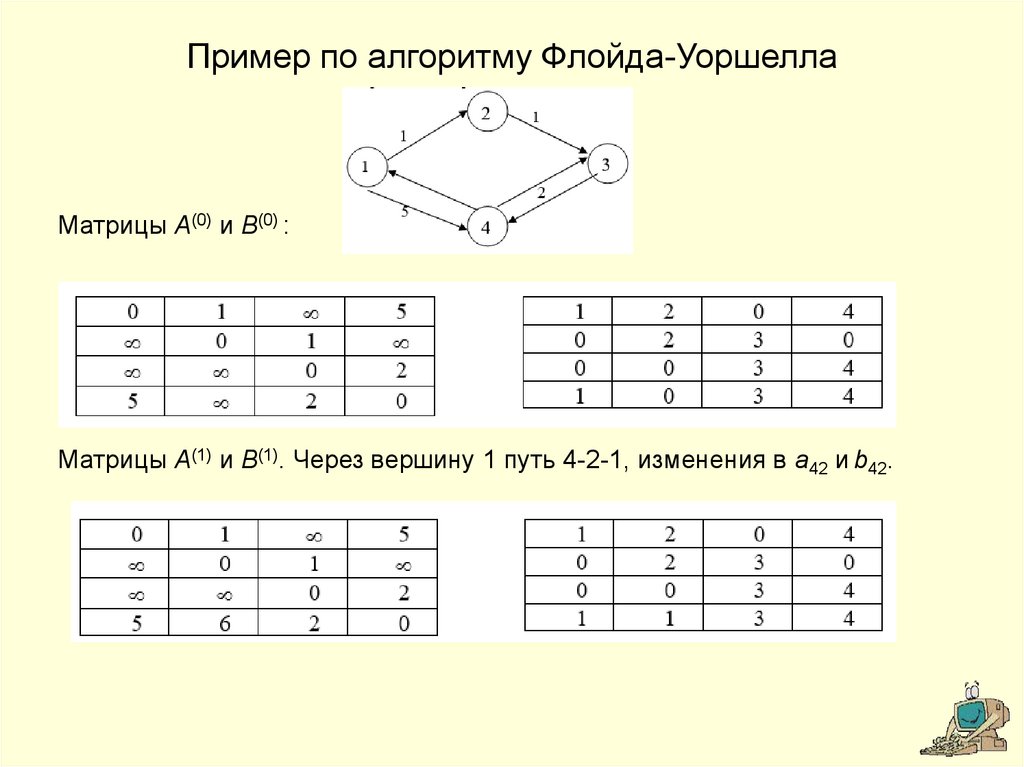
13. Пример по алгоритму Флойда-Уоршелла

Матрицы A(0) и B(0) :
Матрицы A(1) и B(1). Через вершину 1 путь 4-2-1, изменения в a42 и b42.

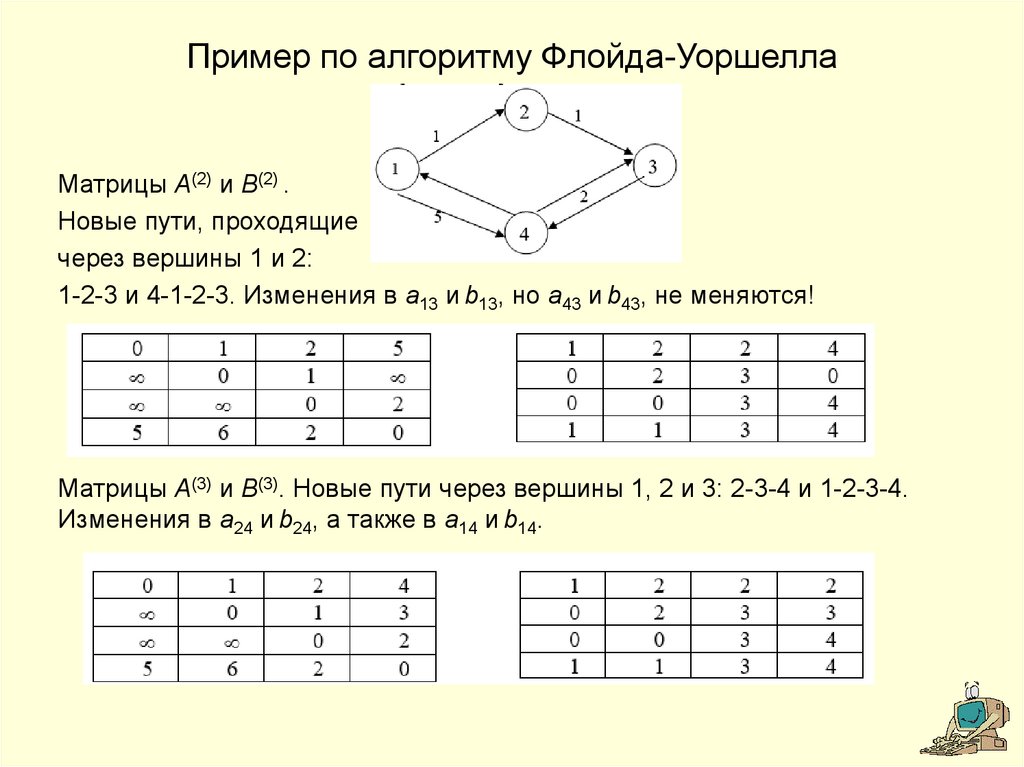
14. Пример по алгоритму Флойда-Уоршелла

Матрицы A(2) и B(2) .
Новые пути, проходящие
через вершины 1 и 2:
1-2-3 и 4-1-2-3. Изменения в a13 и b13, но a43 и b43, не меняются!
Матрицы A(3) и B(3). Новые пути через вершины 1, 2 и 3: 2-3-4 и 1-2-3-4.
Изменения в a24 и b24, а также в a14 и b14.

15. Пример по алгоритму Флойда-Уоршелла

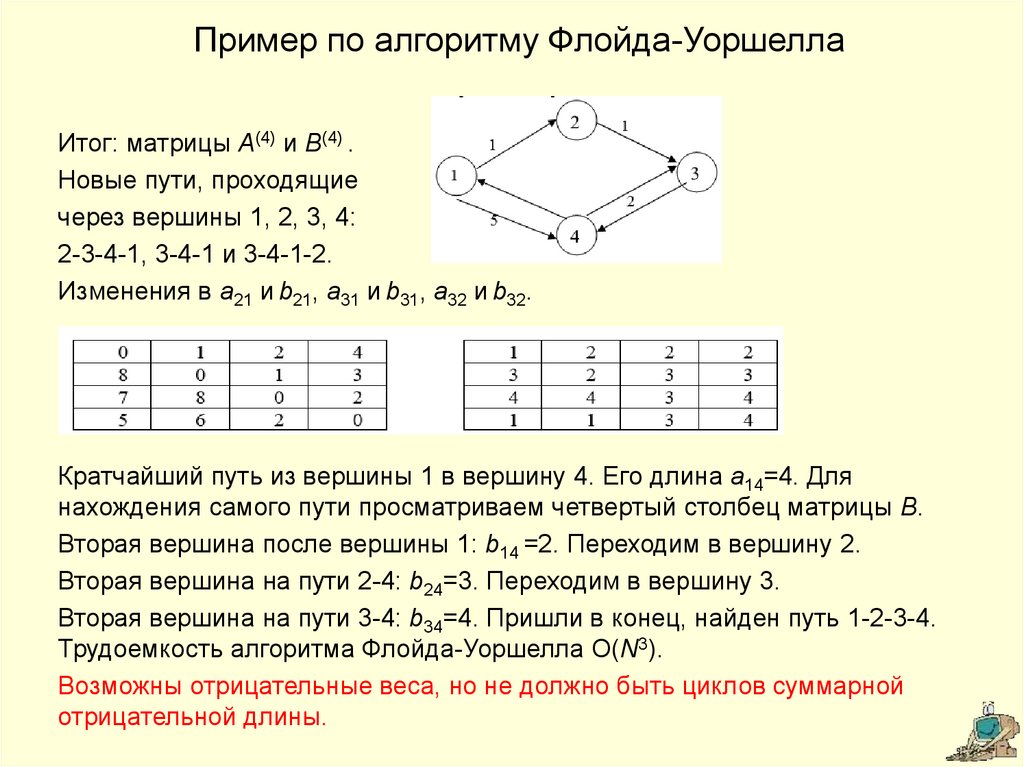
Итог: матрицы A(4) и B(4) .
Новые пути, проходящие
через вершины 1, 2, 3, 4:
2-3-4-1, 3-4-1 и 3-4-1-2.
Изменения в a21 и b21, a31 и b31, a32 и b32.
Кратчайший путь из вершины 1 в вершину 4. Его длина a14=4. Для
нахождения самого пути просматриваем четвертый столбец матрицы B.
Вторая вершина после вершины 1: b14 =2. Переходим в вершину 2.
Вторая вершина на пути 2-4: b24=3. Переходим в вершину 3.
Вторая вершина на пути 3-4: b34=4. Пришли в конец, найден путь 1-2-3-4.
Трудоемкость алгоритма Флойда-Уоршелла O(N3).
Возможны отрицательные веса, но не должно быть циклов суммарной
отрицательной длины.

16.

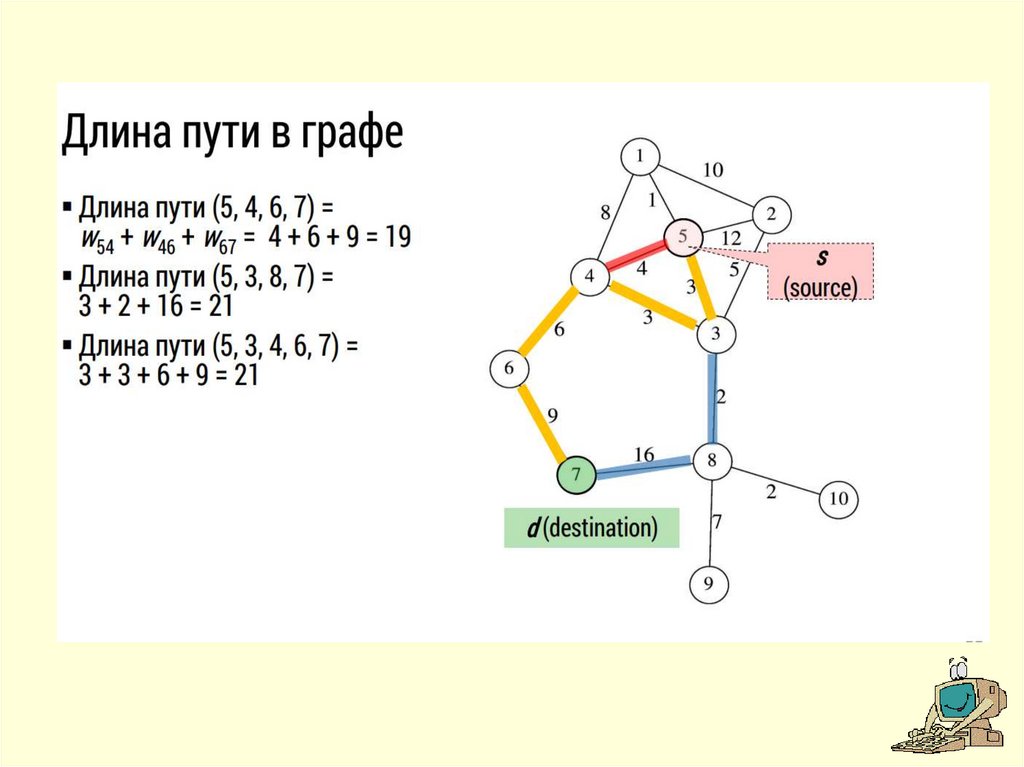
Задача на обходы графа
Имеется ориентированный граф. Длиной пути считается число имеющихся
в нем звеньев. Заданы две разные вершины (начало и конец) и целое
число L, определяющее макимально допустимую длину. Требуется
построить минимальный граф путей ограниченной длины из начала в
конец, то есть усечь граф так, чтобы:
• новый граф содержал все пути, соединяющие начало с концом и
имеющие длины, не превышающие макимально допустимую;
• исключение любой вершины или дуги нового графа вело к нарушению
первого условия.
Решение:
1) Поиском в ширину для каждой вершины Vi находятся минимальные
длины ui и vi от начала до Vi и от Vi до конца.
2) В цикле по вершинам: Vi вместе с инцидентными дугами отсекается,
если ui + vi > L.
3) В цикле по дугам: дуга i → j отсекается, если ui + vj +1 > L.

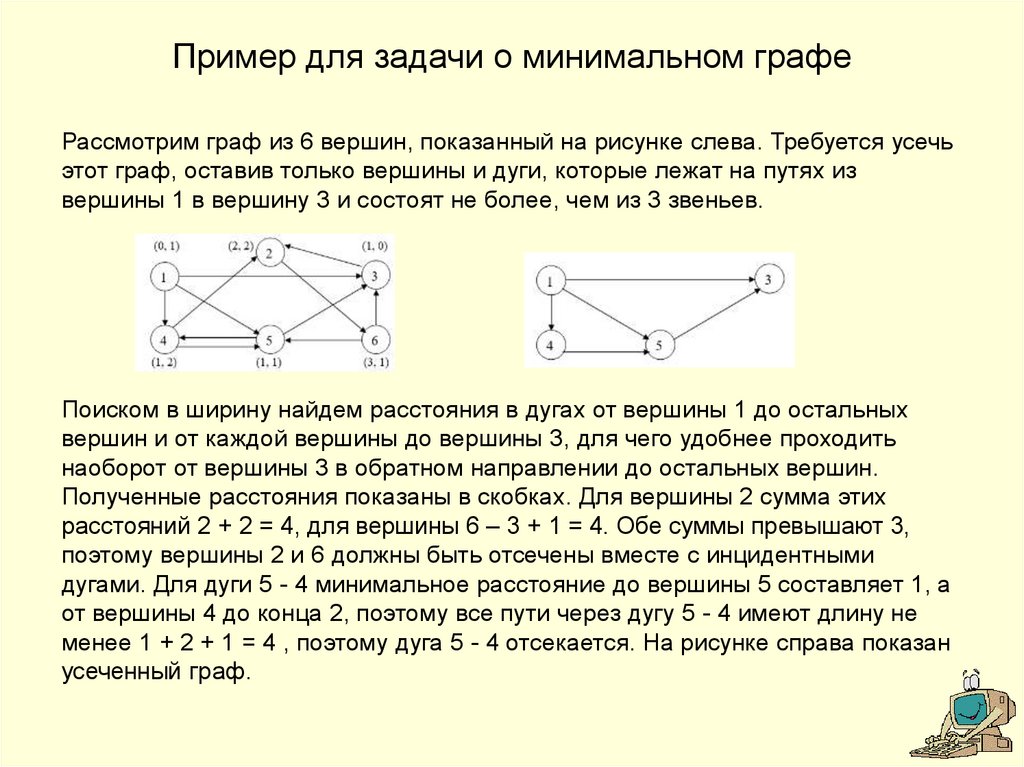
17. Пример для задачи о минимальном графе

Рассмотрим граф из 6 вершин, показанный на рисунке слева. Требуется усечь
этот граф, оставив только вершины и дуги, которые лежат на путях из
вершины 1 в вершину 3 и состоят не более, чем из 3 звеньев.
Поиском в ширину найдем расстояния в дугах от вершины 1 до остальных
вершин и от каждой вершины до вершины 3, для чего удобнее проходить
наоборот от вершины 3 в обратном направлении до остальных вершин.
Полученные расстояния показаны в скобках. Для вершины 2 сумма этих
расстояний 2 + 2 = 4, для вершины 6 – 3 + 1 = 4. Обе суммы превышают 3,
поэтому вершины 2 и 6 должны быть отсечены вместе с инцидентными
дугами. Для дуги 5 - 4 минимальное расстояние до вершины 5 составляет 1, а
от вершины 4 до конца 2, поэтому все пути через дугу 5 - 4 имеют длину не
менее 1 + 2 + 1 = 4 , поэтому дуга 5 - 4 отсекается. На рисунке справа показан
усеченный граф.

18. Спасибо за внимание!