Similar presentations:
Применение алгоритма Флойда для решения задачи о кратчайшем пути
1. Применение алгоритма Флойда для решения задачи о кратчайшем пути
ЯЛ
Д У ТИ
А П
Д
Й М
О
Е
Л
Ш
Ф
А АЙ
М ТЧ
Т
И РА
Р
О К
Г
О
Л
А ЧИ
Е
И ДА
Н
Е ЗА
Н
Е Я
М
И
Н
И
ПР ШЕ
РЕ
2.
Актуальностьзадачи о
кратчайшем пути
3.
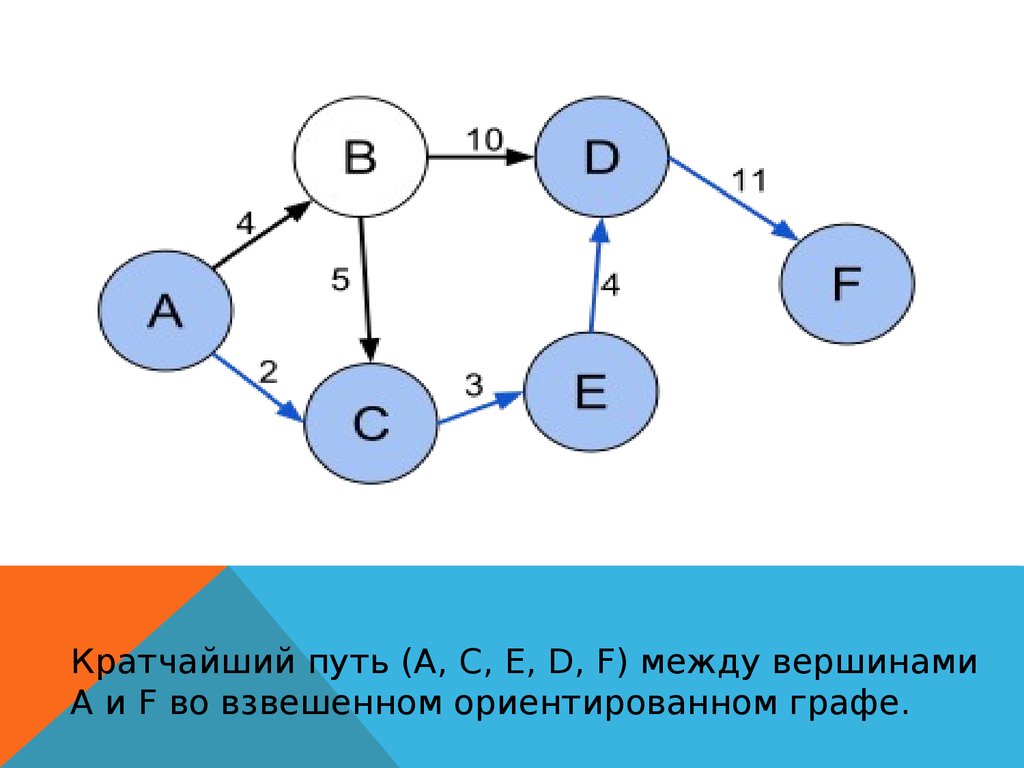
Кратчайший путь (A, C, E, D, F) между вершинамиA и F во взвешенном ориентированном графе.
4. Алгоритмы нахождения кратчайшего пути
АЛГОРИТМЫ НАХОЖДЕНИЯ КРАТЧАЙШЕГОПУТИ
1) Алгоритм Форда-Беллмана
2) Алгоритм Дейкстры
3) Алгоритм Флойда
5. Роберт флойд 8.06.1936 – 25.09.2001
РОБЕРТФЛОЙД
8.06.1936
–
25.09.2001
6.
for (k = 0; k < n; k++)for (i = 0; i < n; i++)
for (j = 0; j < n; j++)
if (array[i, j] > array[i, k] + array[k, j])
array[i, j] = array[i, k] + array[k, j];
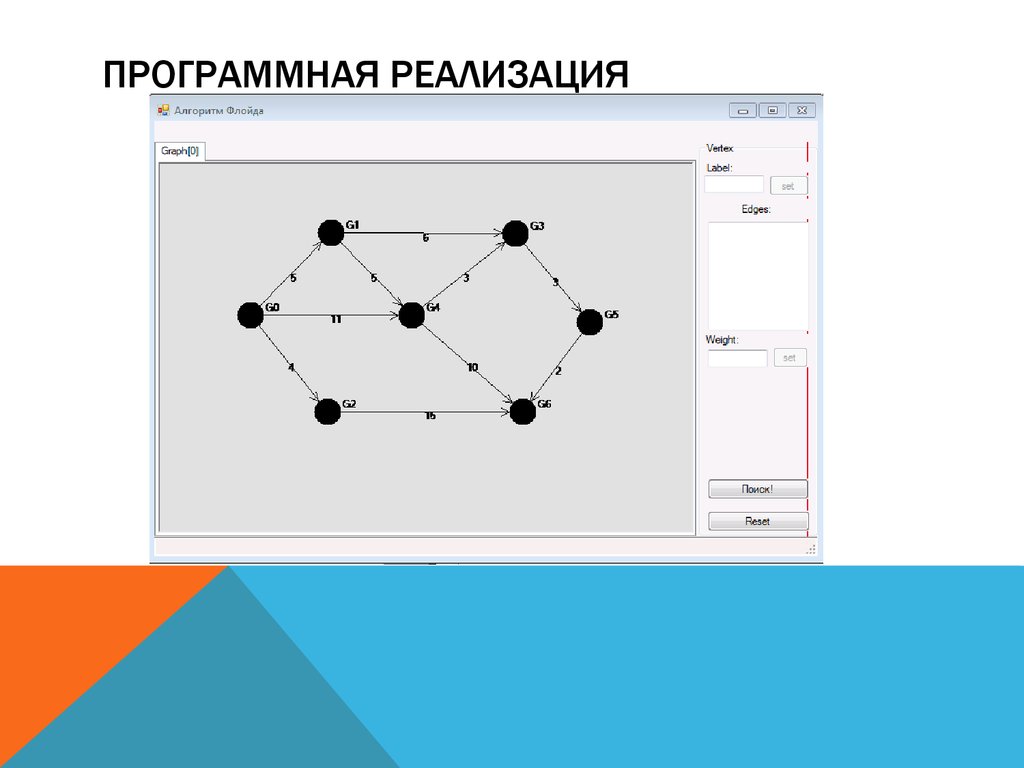
7. Программная реализация
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ8.
9. Заключение
ЗАКЛЮЧЕНИЕ1)Освоение алгоритма и его реализация
2)Осуществление отрисовки графа
возможно улучшение алгоритма для
применения на практике
Выполнил студент 3 курса, 61 группы
Бельков Дмитрий







 mathematics
mathematics programming
programming








