Similar presentations:
Алгоритм Флойда-Уоршалла
1. Алгоритм Флойда-Уоршалла
Находит кратчайшие расстояния междувсеми парами вершин графа
Идея: Строится специальная матрица D,
элементы которой – кратчайшие пути
между всевозможными парами вершин
графа G. При определении кратчайшего
пути выбирается минимум из «прямого»
расстояния между смежными
вершинами vi и vj и суммарного
расстояния при проходе через
дополнительную вершину. Затем –
более длинные пути и т.д.
2.
Обозначим через d (m)длину кратчайшегоij
пути из vi в vj с промежуточными вершинами
во множестве {v1,…,vm}.
Алгоритм использует три правила:
1)
(0 )
di j ai j
- вес дуги, соединяющей
вершины vi и vj (т.е. первоначально матрица
D – это исходная матрица весов).
3.
2)d
( m 1)
ij
min d
( m)
ij
,d
( m)
i ,m 1
d
( m)
m 1, j
3) Длина кратчайшего пути из вершины vi
в вершину vj:
d vi , v j d
(n)
i j
Алгоритм строит матрицу за n шагов, т.е.
строится матрица D(1) , …, D(n) =D.
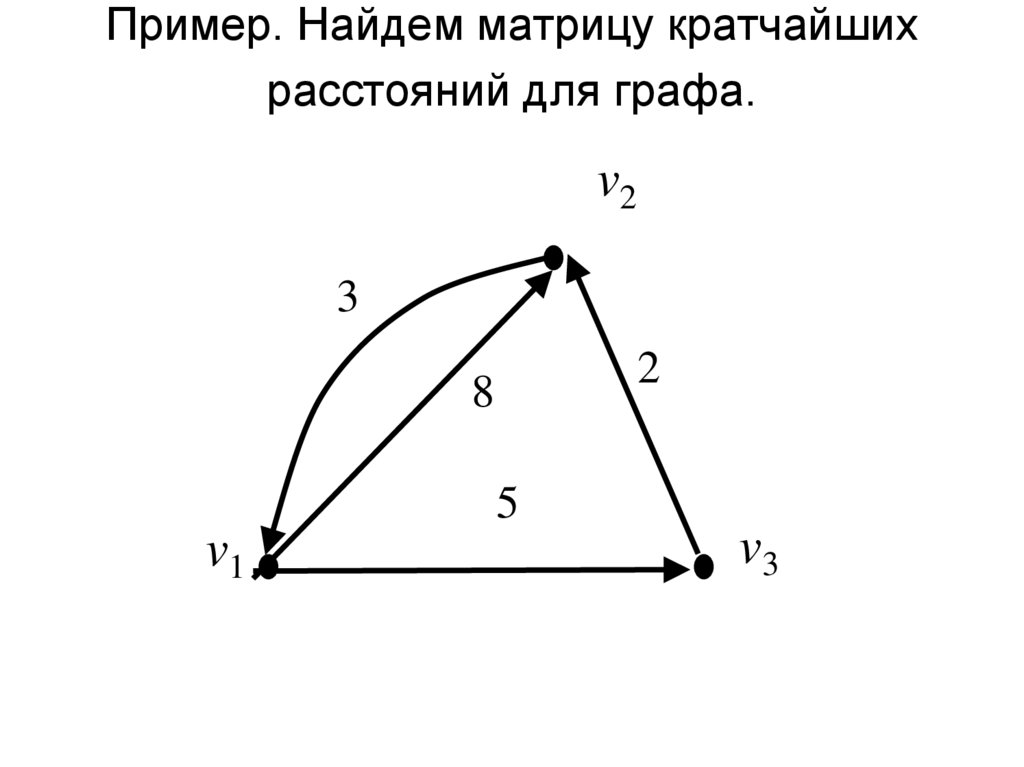
4. Пример. Найдем матрицу кратчайших расстояний для графа.
v23
2
8
5
v1
v3
5.
v1v2
v3
0 8 5 v1
(0)
D 3 0 v2
2 0 v
3
6.
Элементы матрицы D(1) находим по правилу:( 0)
i j
(0)
11
(0)
11
d
(1)
12
(0)
12
(0)
11
(0)
12
(1)
13
(0)
13
(0)
11
(0)
13
(1)
21
(0)
21
(0)
21
(0)
11
(1)
22
(0)
22
(0)
21
(0)
12
(1)
23
(0)
23
(0)
21
(0)
13
(1)
i j
min d
(1)
11
d
,d
d
( 0)
1j
min( 0,0) 0
d min d , d d min( 8,8) 8
d min d , d d min( 5,5) 5
d min d , d d min( 3,3 0) 3
d min d , d d min( 0,3 8) 0
d min d , d d min( ,3 5) 8
d
min d , d
( 0)
i1
(0)
11
7.
d min d , dd min d , d
d
(1)
31
min d , d
(0)
31
(0)
31
(1)
32
(0)
32
(0)
31
(1)
33
(0)
33
(0)
31
min( , 0)
d min( 2, 8) 2
d min( 0, 5) 0
d
(0)
11
(0)
12
(0)
13
8.
0(1)
D 3
8
0
2
5
8
0
Элементы матрицы D(2) находим по правилу:
d
( 2)
ij
min d , d
(1)
ij
(1)
i2
d
(1)
2j
9.
min d , d d min( 8,8 0) 8min d , d d min( 5,8 8) 5
min d , d d min( 3,0 3) 3
min d , d d min( 0,0 0) 0
min d , d d min( 8,0 8) 8
min d , d d min( ,2 3) 5
min d , d d min( 2,2 0) 2
min d , d d min( 0,2 8) 0
( 2)
(1)
(1)
(1)
d11
min d11
, d12
d 21
min( 0,8 3) 0
( 2)
12
d
( 2)
13
d
d
( 2)
21
d
( 2)
22
d
( 2)
23
d
( 2)
31
d
( 2)
32
d
( 2)
33
(1)
12
(1)
12
(1)
22
(1)
13
(1)
12
(1)
23
(1)
21
(1)
22
(1)
21
(1)
22
(1)
22
(1)
22
(1)
23
(1)
22
(1)
23
(1)
31
(1)
32
(1)
21
(1)
32
(1)
32
(1)
22
(1)
33
(1)
32
(1)
23
10.
0 8 5( 2)
D 3 0 8
5 2 0
Элементы матрицы D(3) находим по правилу:
d
( 3)
ij
min d
( 2)
ij
,d
( 2)
i3
d
( 2)
3j
11.
( 3)11
d
( 3)
12
d
( 3)
13
d
d
( 3)
21
d
( 3)
22
d
( 3)
23
( 3)
d31
d
( 3)
32
d
( 3)
33
,d
min d , d
min d , d
min d , d
min d , d
min d , d
min d , d
min d , d
min d , d
( 2)
11
( 2)
13
d
( 2)
31
min d
( 2)
12
( 2)
13
d
( 2)
32
( 2)
13
( 2)
13
d
( 2)
33
( 2)
21
( 2)
23
d
( 2)
31
( 2)
22
( 2)
23
d
( 2)
32
( 2)
23
( 2)
23
d
( 2)
33
( 2)
31
( 2)
33
( 2)
d31
( 2)
32
( 2)
33
d
( 2)
32
( 2)
33
( 2)
33
d
( 2)
33
min( 0,5 5) 0
min( 8,5 2) 7
min( 5,5 0) 5
min( 3,8 5) 3
min( 0,8 2) 0
min( 8,8 0) 8
min( 5,0 5) 5
min( 2,2 0) 2
min( 0,0 0) 0
12.
0 7 5( 3)
( 3)
D 3 0 8 , D D
5 2 0
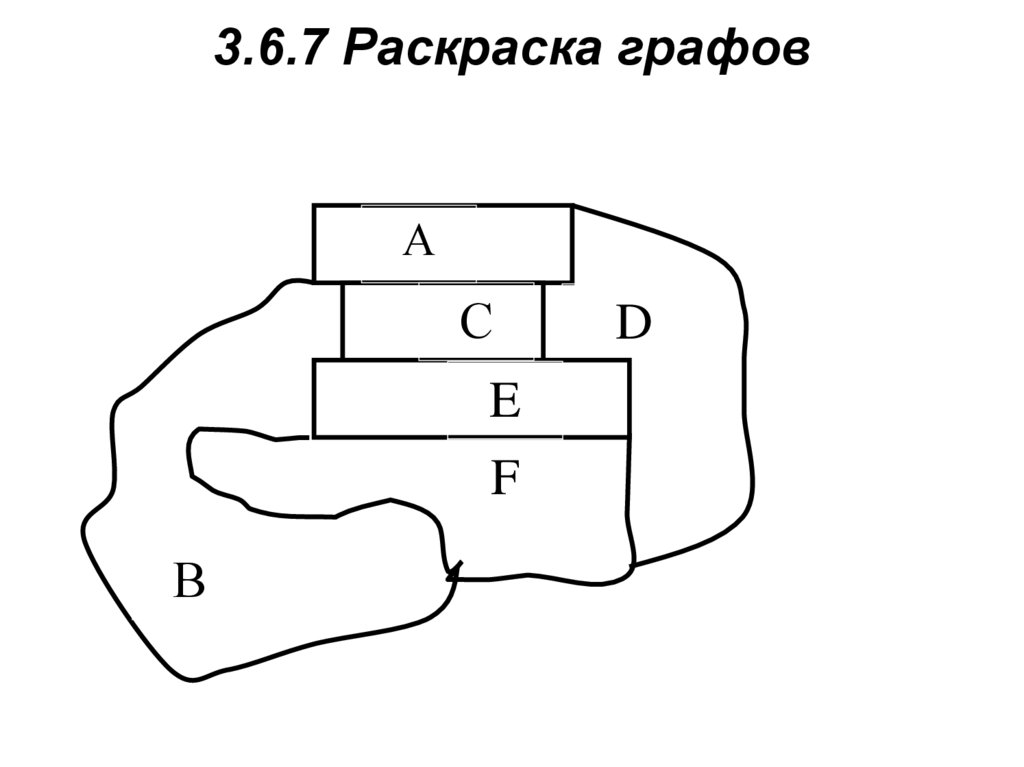
13. 3.6.7 Раскраска графов
АС
E
F
В
D
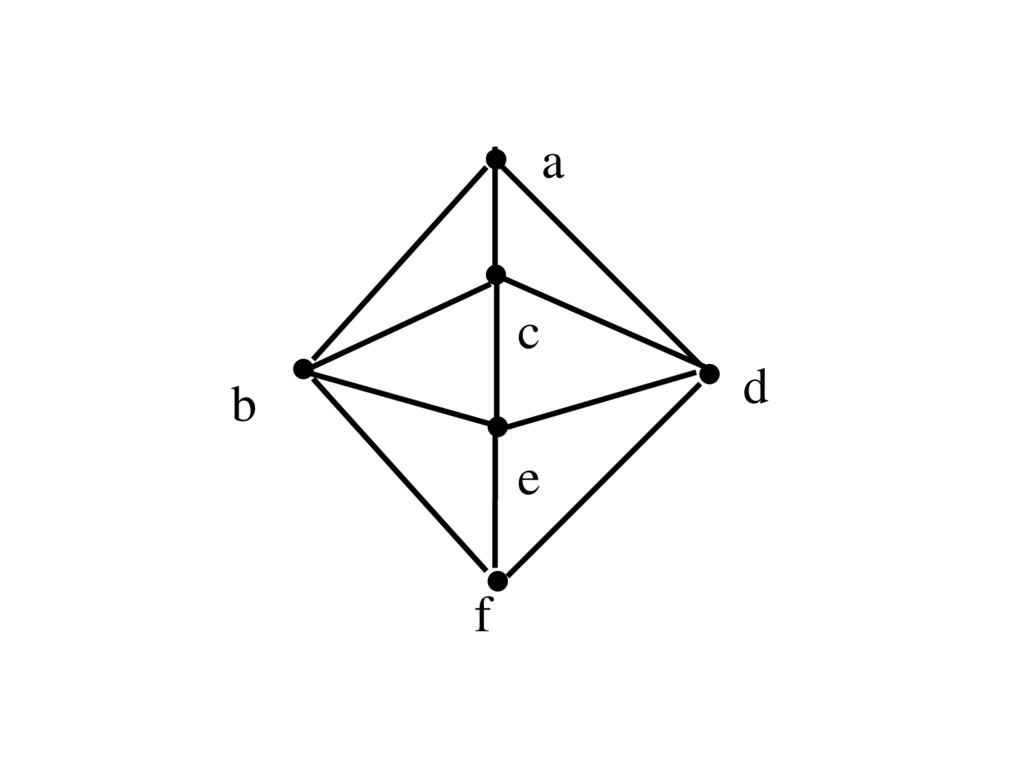
14.
ac
d
b
e
f
15.
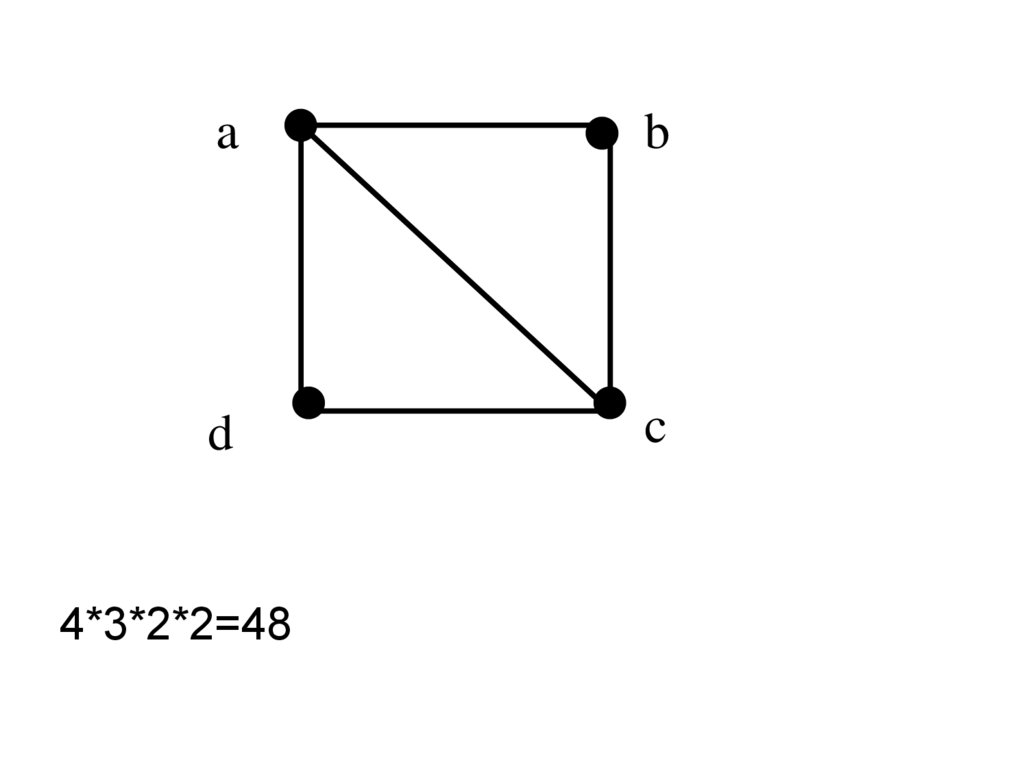
ab
d
c
4*3*2*2=48
16.
Раскраской графа G называетсяокрашивание вершин графа G, такое, что
никакие две смежные вершины не окрашены
в один цвет.
Пусть СG( ) обозначает количество способов
раскраски графа G с использованием
цветов, так, что никакие две соседние
вершины не окрашены в разные цвета. Для
фиксированного графа G это
полиномиальная функция от .
17.
Само при этом называется хроматическимчислом.
Хроматическое число графа – это
наименьшее положительное число n, такое
что СG(n) 0.
Проблема четырёх красок эквивалентна
утверждению, что СG(4) 0 для
произвольного графа.



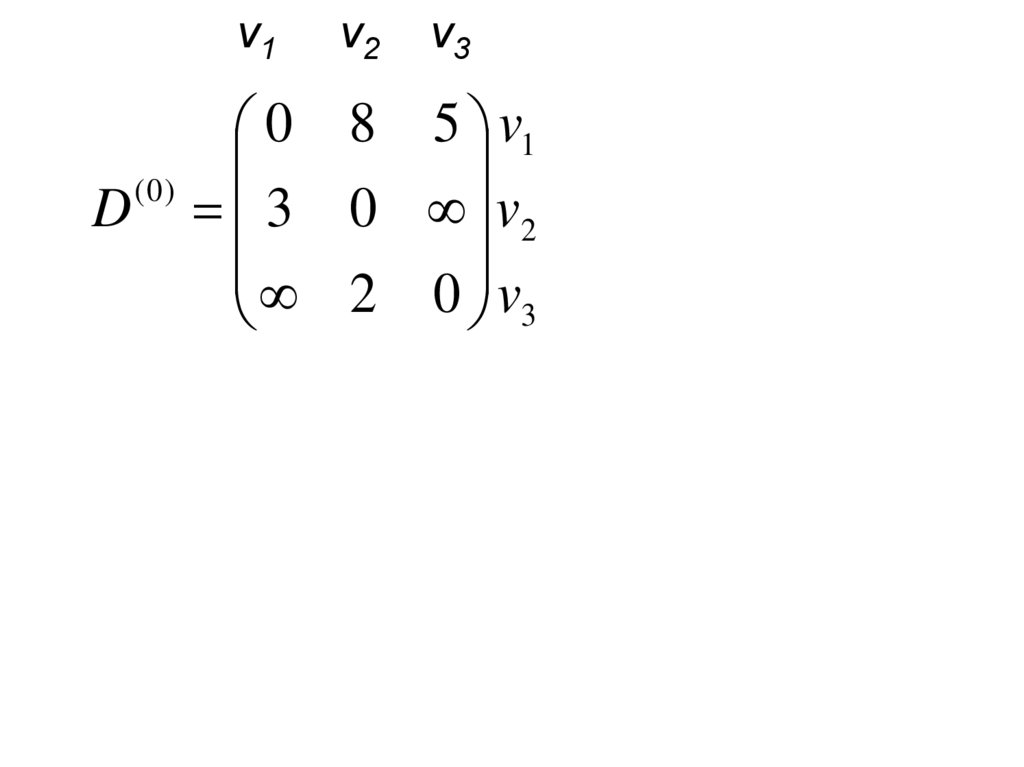

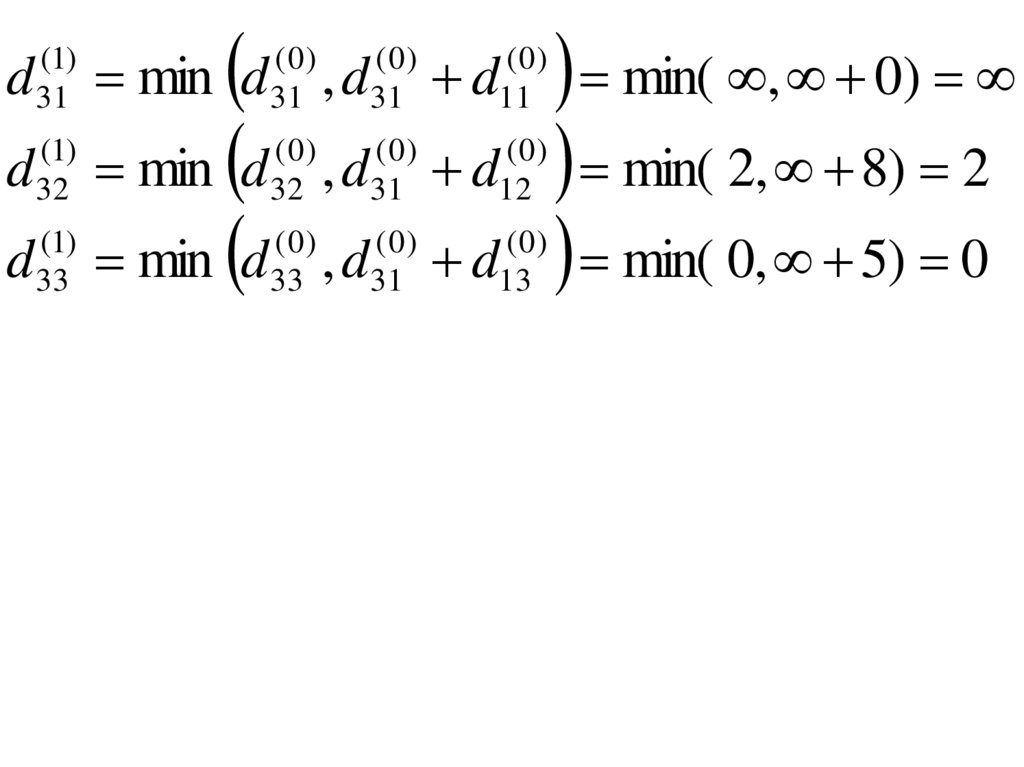

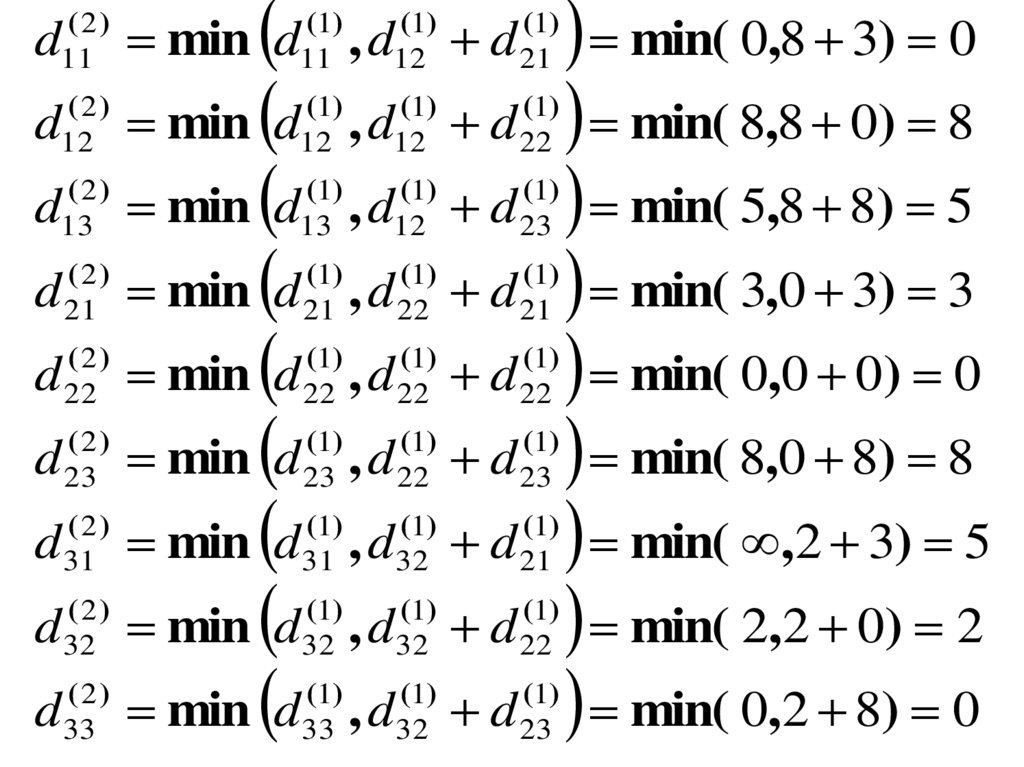

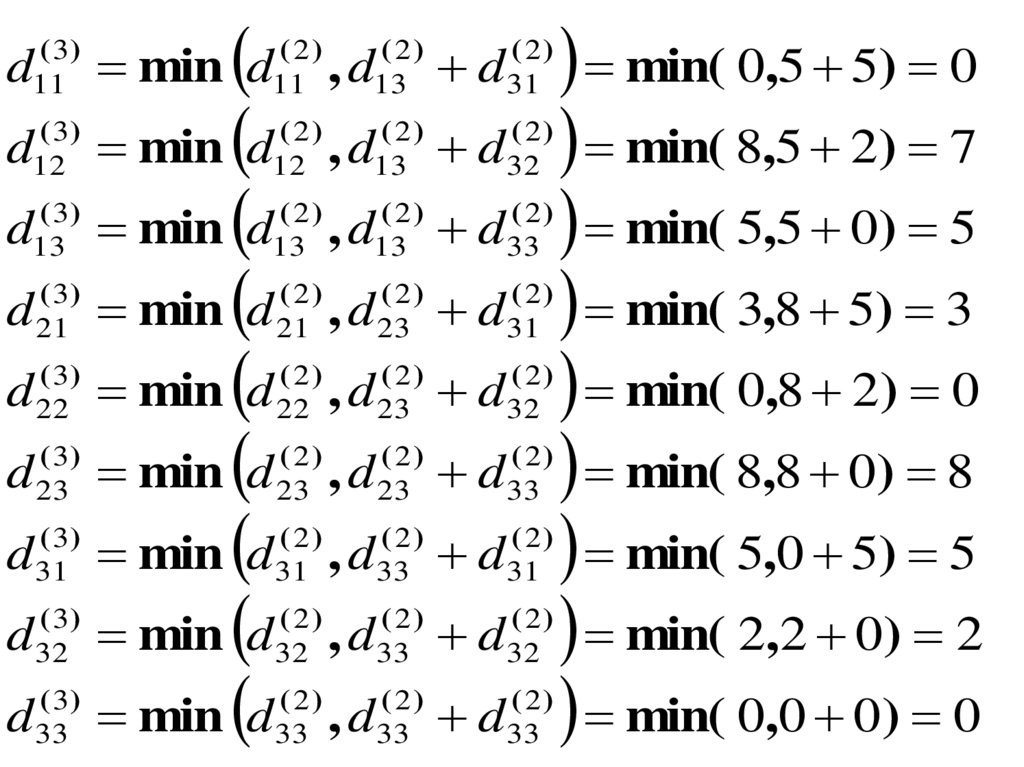
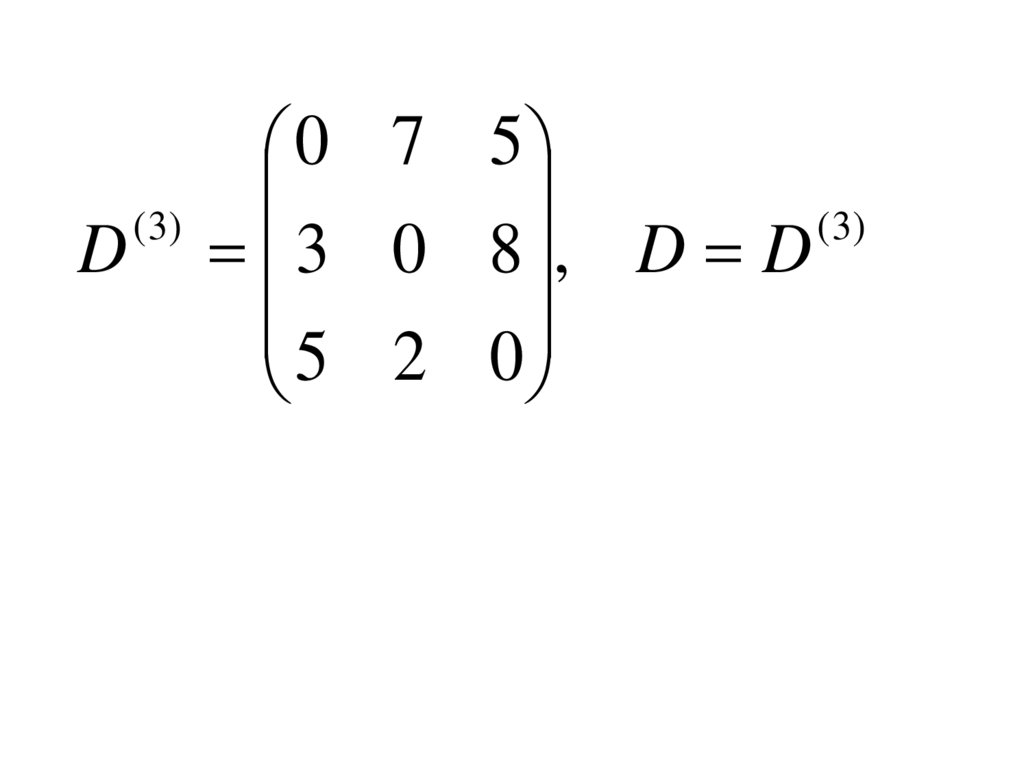


 mathematics
mathematics








