Моделирование на графах

1. МОДЕЛИРОВАНИЕ НА ГРАФАХ

ИНФОРМАЦИОННОЕ МОДЕЛИРОВАНИЕ

2. Ключевые слова

МК
Ключевые слова
алгоритм Дейкстры
динамическое программирование
теория игр
стратегия игры
дерево игры
выигрышная стратегия
выигрышная позиция игрока
проигрышная позиция игрока

3. Кратчайший путь между вершинами графа

МК
Кратчайший путь между вершинами графа
Поиск оптимального транспортного маршрута, проектирование
инженерных сетей и линий электропередач приводят к задаче поиска
кратчайшего пути.
Путь между вершинами А и В графа считается кратчайшим, если:
• эти вершины соединены минимальным числом ребер (в случае, если
граф не является взвешенным)
• сумма весов ребер, соединяющих эти вершины, минимальна (для
взвешенного графа)
Построение дерева решений
Алгоритмы поиска
кратчайшего пути
Алгоритм Дейкстры
Метод динамического
программирования

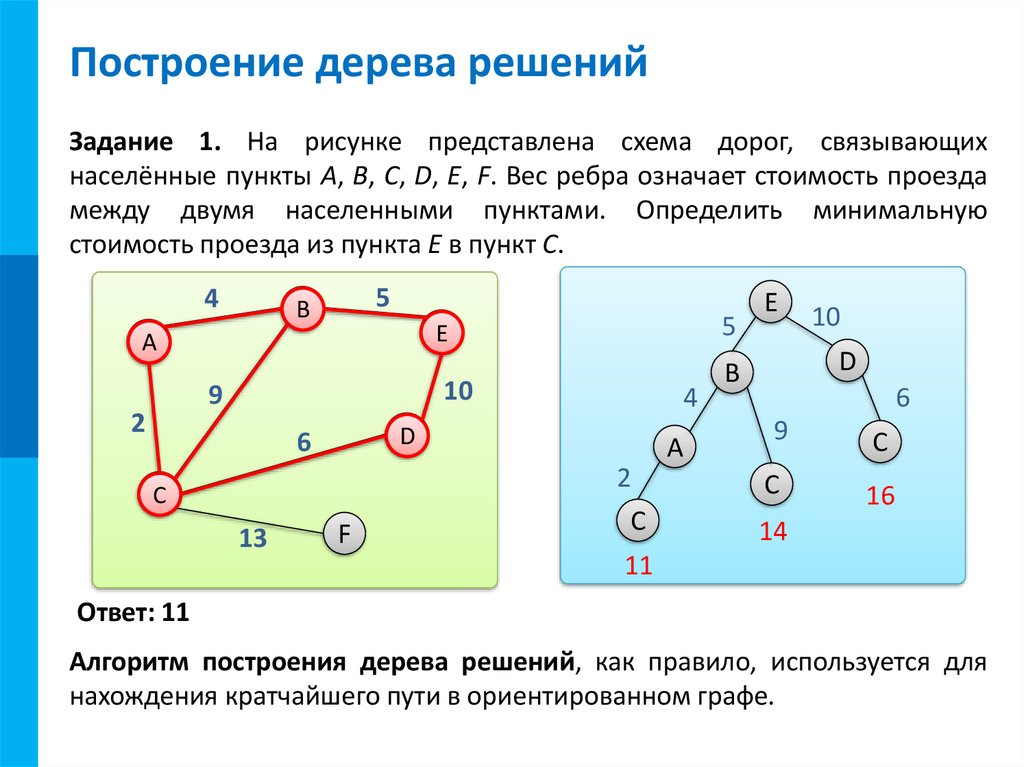
4. Построение дерева решений

МК
Построение дерева решений
Задание 1. На рисунке представлена схема дорог, связывающих
населённые пункты A, B, C, D, E, F. Вес ребра означает стоимость проезда
между двумя населенными пунктами. Определить минимальную
стоимость проезда из пункта E в пункт C.
4
5
B
A
10
9
2
5
E
4
D
6
A
2
C
13
F
C
E
10
D
B
6
9
C
С
16
14
11
Ответ: 11
Алгоритм построения дерева решений, как правило, используется для
нахождения кратчайшего пути в ориентированном графе.

5. Алгоритм Дейкстры

МК
Алгоритм Дейкстры
Задание 2. Определить
минимальное расстояние от
вершины A до F.
?
∞
2
∞
7
E
Можно B ли, 5 используя
2Дейкстры, найти
алгоритм
9
A 0
10от
наибольшее
расстояние
13
вершины-источника
до
2
∞ C
13
11
остальных
вершин? D 17
∞
15
Какие 4 следует
внести
6
изменения? F ∞
15
Можно ли этот алгоритм
Алгоритм
Дейкстры
служит
применить
к
орграфу
- рассматриваемая
вершина
для нахождения графу)?
кратчай(ориентированному
вершина
шего- рассмотренная
пути между вершиной
Ответ: 15
(источником)
и
всеми
- непосещённая вершина
остальными
вершинами
графа.
Начало
Метка источника равна 0
Остальные метки равны ∞
Есть
непосещенные?
Да
Найти вершину с
минимальной меткой
Определить минимальное расстояние
до смежных вершин
Отметить вершину
как рассмотренную
Конец

6. Метод динамического программирования

МК
Метод динамического программирования
Задание 3. Все улицы одного из кварталов города N прямые с
Решение методом динамического
односторонним движением и пересекаются под прямым углом. Если не
программирования опирается на те же
поворачивать, то можно проехать с южной окраины на северную или с
утверждения.
западной на восточную. Длины переулков равны, но каждый участок
При заполнении
будем задачи
двигаться от
Рекурсивное
решение
этой
характеризуется количеством
ям на дороге.
Необходимо
выбрать лучший
левогопонижнего
угла
к правому
не определить
оптимально
скорости
выполнения.
Как
движения?
маршрут проезда от пункта
A в пункт B. маршрут
верхнему.
13
5
8
16
14
3
1
5
13
2
7
2
A
0
9
4
15
2
15
8
15
1
11
3
7
14
4
10
3
25
B
10
4
8
4
4
11
10
6
17
9
16
Попасть в вершину B можно только из
2+7<4+8
значение
стартовой
(зеленой)
двух
вершин.
Значение
лучшего
Вариант
проезда
отравно
начала
движения
вершины
A[1, 1]
нулю
вариантаназависит
тольконаотвосток
веса
сначала
север, непотом
ребер,
но и – от сумма
того, сзначений
каким
лучше.
значение
Pascal
Excel
«результатом»
можно
добраться до
предшествующих
участков
этих двух вершин.
значение врекурсивное
вершине X[i, решение
j] равно
Существует
из значений вершин
этойменьшему
задачи.
X[i-1, j] и X[i, j-1] с учетом весовых
значений дуг, направленных к X[i, j]

7. Метод динамического программирования

МК
Знакомство с теорией игр
Теория игр — раздел современной математики, связанный с решением
многих задач экономики, социологии, политологии, биологии,
искусственного интеллекта и ряда других областей, где необходимо
изучение поведения человека и животных в различных ситуациях.
Игра выступает в качестве математической модели некоторой ситуации и
понимается как процесс, в котором участвуют две и более стороны,
ведущие борьбу за реализацию своих интересов.

8. Метод динамического программирования

МК
Знакомство с теорией игр
Метки
Отметим
Индекс
Найдем
Для
Клетки
Из
клеток
отмеченных
четырех
клеток
являются
означает
клетки,
такую
эту
клетку
В2позиций
. клетку,
клеток
из
пойти
колипрокак
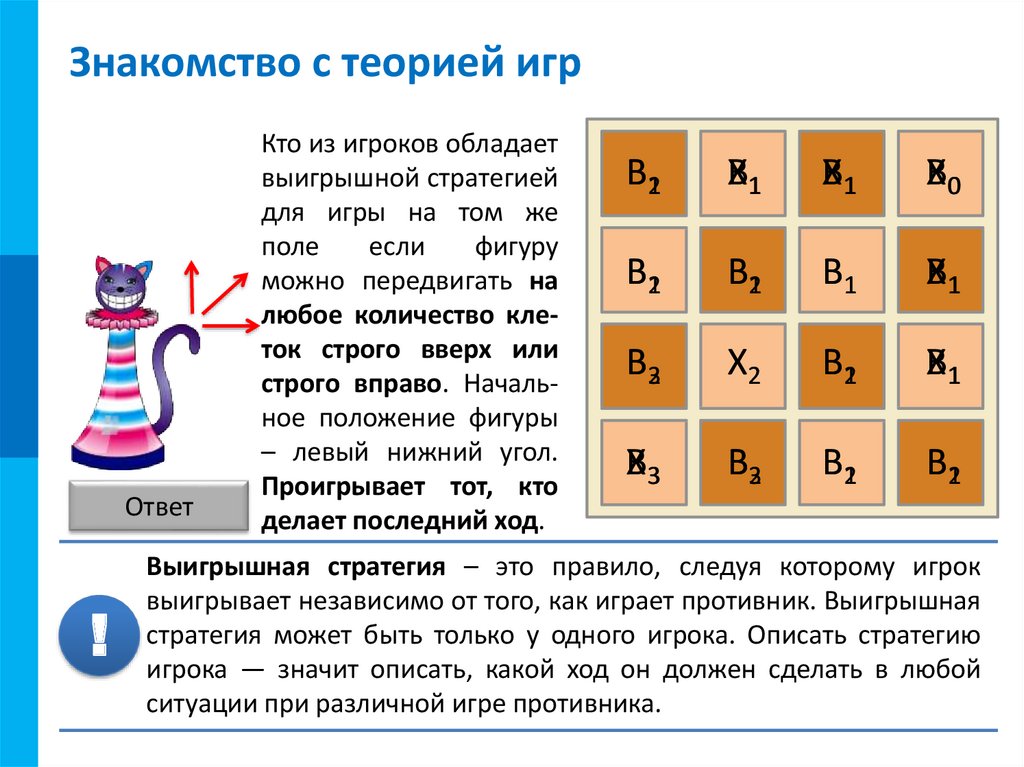
ко- кот предложил сыграть в игру с
Задание
4.можно
Чеширский
В2
X1доски.В1Вы и Xкот
ход
проигрышную
чество
торых
определено
существует
вигрышными
трив различные
которую
можно
ходов
только
возможное
в поставить
один
–означает
из
Xклетки.
этой
(для
ход
одной
фигурой
на
части шахматной
0 один
0
выигрыш
того,
позиции
фигуру
развитие
вариант
(ходящего
Какие
кто
варианты
входа
должен
до
игрока)
позицию
для
игры,
игрока.
развязки
следует
игрока,
сейчас
–при
XЗа
ходите
по
очереди.
0. один ход фигуру можно пере1
занявшего
выполнять
игры.
Отметим
условии
Из
выбрать?
каждой
их
ход).
эту
знаком
существует
грамотной
позицию,
Вклетку
местить
на
одну
в направлении, указанном
1.
В2сделалВ2последний
В1 ход.В1
истрелками.
игры
единственный
обоих
проигрыш
игроков.
вариант
для тот, кто
Выигрывает
соперника.
развития
событий.
Хотите я дам вам
возможность
В3
X2 В2
X1
пойти первым?
В3
В3
В2
В2

9. Знакомство с теорией игр

МК
Знакомство с теорией игр
Ответ
!
Кто
В
таблице
из игроков
представлена
обладает
вся информация
выигрышной
стратегией
об
игре. игры
для
Обозначены
на том все
же
клетки если
поле
являющиеся
фигуру
выигрышными
можно
передвигать
и все
на
клетки, количество
любое
которые кленеобходимо
ток
строго вверх
избегать.
или
Игрок, вправо.
строго
который Начальделает
первый
ное
положение
ход, обладает
фигуры
–выигрышной
левый нижний угол.
стратегией.
Проигрывает
тот, кто
делает последний ход.
В12
X1
В
В1
Х
X0
В
В12
В12
В1
В1
Х
В23
X2
В12
X1
В
В3
Х
В23
В12
В12
Выигрышная стратегия – это правило, следуя которому игрок
выигрывает независимо от того, как играет противник. Выигрышная
стратегия может быть только у одного игрока. Описать стратегию
игрока — значит описать, какой ход он должен сделать в любой
ситуации при различной игре противника.

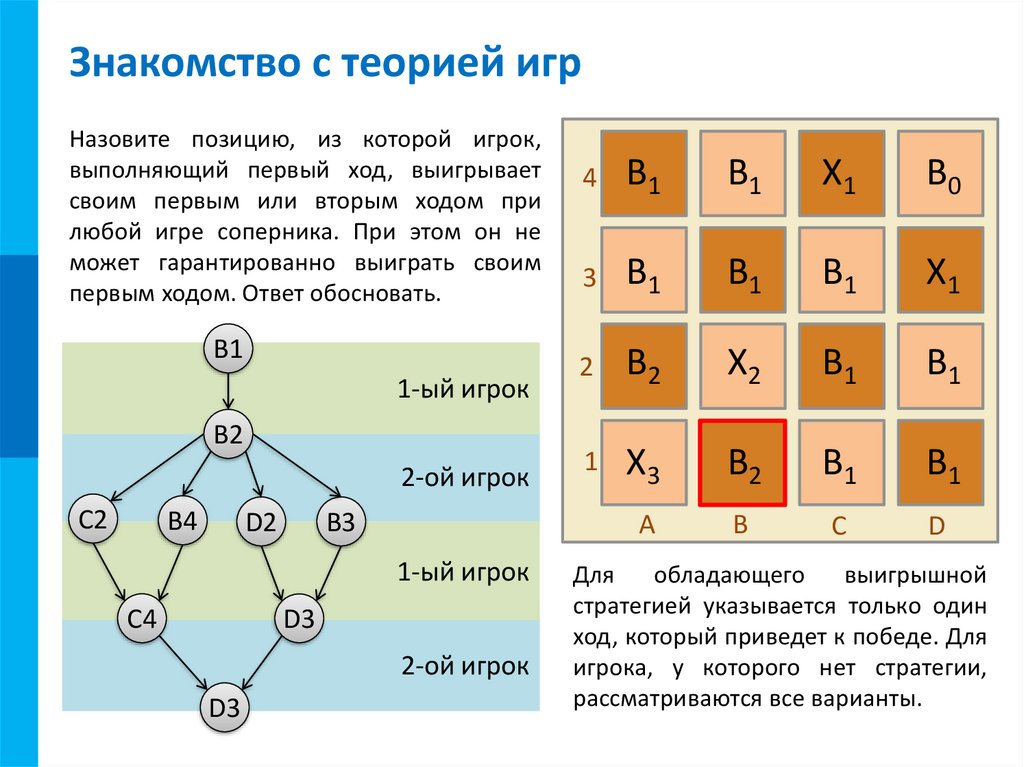
10. Знакомство с теорией игр

МК
Знакомство с теорией игр
Назовите позицию, из которой игрок,
выполняющий первый ход, выигрывает
своим первым или вторым ходом при
любой игре соперника. При этом он не
может гарантированно выиграть своим
первым ходом. Ответ обосновать.
B1
1-ый игрок
B2
2-ой игрок
C2
B4
D2
B3
1-ый игрок
D3
C4
2-ой игрок
D3
4
В1
В1
Х1
В0
3
В1
В1
В1
Х1
2
В2
X2
В1
В1
1
Х3
В2
В1
В1
A
B
C
D
Для
обладающего
выигрышной
стратегией указывается только один
ход, который приведет к победе. Для
игрока, у которого нет стратегии,
рассматриваются все варианты.

11.

МК
Знакомство с теорией игр
Признаки игры
• присутствие нескольких игроков
• неопределённость
поведения
игроков, связанная с имеющимися
у каждого из них несколькими
вариантами действий
• различие (несовпадение) интересов игроков
• взаимосвязанность
поведения
игроков (результат, получаемый
каждым из них, зависит от
поведения всех игроков)
• наличие
правил
поведения,
известных всем игрокам

12. Знакомство с теорией игр

МК
Самое главное
Графы как информационные модели находят широкое применение во
многих сферах нашей жизни. С их помощью можно планировать
оптимальные транспортные маршруты, кратчайшие объездные пути,
расположение торговых точек и других объектов.
Путь между вершинами А и В графа считается кратчайшим, если эти
вершины соединены минимальным числом ребер (в случае, если граф не
является взвешенным), или если сумма весов ребер, соединяющих эти
вершины, минимальна (для взвешенного графа).
Для определения кратчайшего пути между вершинами графа
используются алгоритм построения дерева решений, алгоритм Дейкстры,
метод динамического программирования и другие алгоритмы.
Важную роль в решении многих задач экономики, социологии,
политологии, биологии, искусственного интеллекта и ряда других
областей, где необходимо изучение поведения человека и животных в
различных ситуациях, играет теория игр.

13. Знакомство с теорией игр

МК
Самое главное
Игра, выступающая в качестве математической модели, характеризуется:
1) присутствием нескольких игроков;
2) неопределённостью, связанной с поведением игроков, у каждого из
которых есть несколько вариантов действий;
3) различием (несовпадением) интересов игроков;
4) взаимосвязанностью поведения игроков (результат, получаемый
каждым из них, зависит от поведения всех игроков);
5) наличие правил поведения, известных всем игрокам.
Игра может быть представлена в виде дерева, каждая вершина которого
соответствует ситуации выбора игроком своей стратегии. В играх с полной
информацией участники знают все ходы, сделанные до текущего момента,
равно как и возможные стратегии противников, что позволяет им
предсказать варианты развития игры. Выигрышная стратегия — это
правило, следуя которому игрок выигрывает независимо от того, как
играет противник.

14. Самое главное

МК
Вопросы и задания
5
7
2
6
За посещение
каждой комнаты лабиринта
1 число очков.
3 Найдите
9 такой путь,
4
снимается разное
при котором игрок теряет минимальное число
очков.
Нажмите кнопку «Старт» и проведите указатель
6
11
5
3
мыши по найденному
маршруту.
Старт
1
3
9
4
3
1
9
7

15. Самое главное

МК
Информационные источники
http://centr-nauk.ru/images/14.jpg
http://boredomsolved.co.uk/wp-content/uploads/2015/05/family-game-588908_1280-1024x664.jpg
http://rorganise.esy.es/wp-content/uploads/2015/02/microsoft-excel-logo.jpg
http://4.bp.blogspot.com/-CMpRQ1PVVco/VppPcuE14AI/AAAAAAAASA4/iWlkM-W1kWk/s1600/smiley-taking-a-bow.png
http://super-partnerki.ru/wp-content/uploads/2016/09/Kije8X6yT.png