Similar presentations:
Операция двоичного сложения и её свойства
1. Двоичное сложение. Многочлен Жегалкина
Операция двоичногосложения и её свойства.
Многочлен Жегалкина.
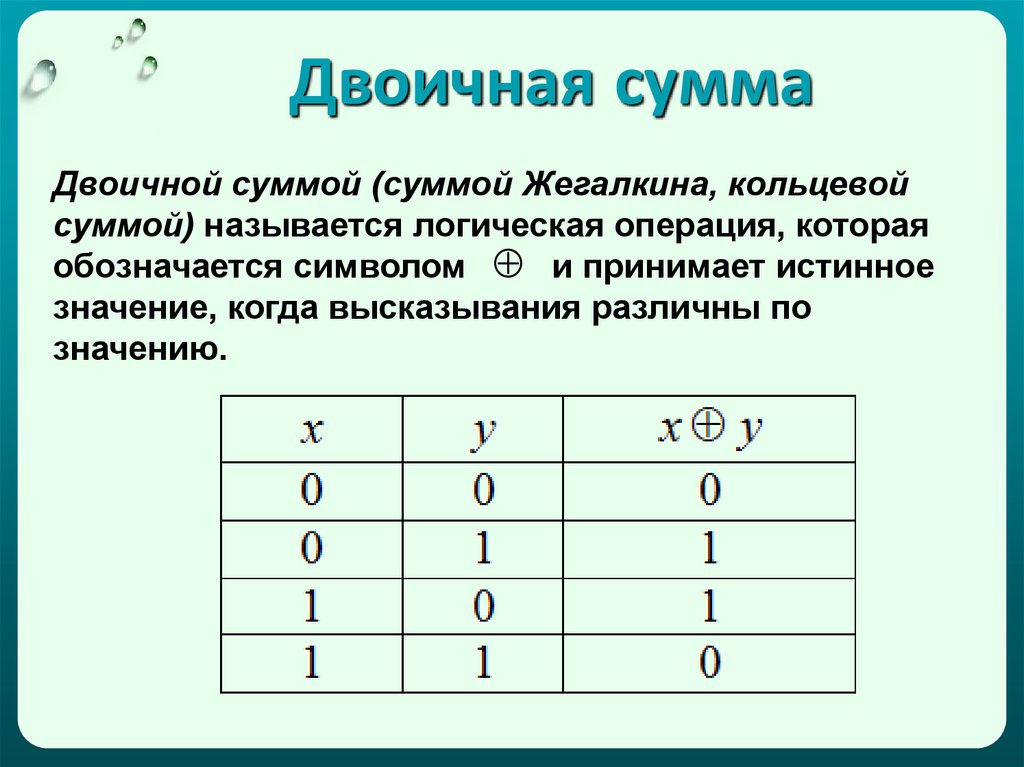
2. Двоичная сумма
Двоичной суммой (суммой Жегалкина, кольцевойсуммой) называется логическая операция, которая
обозначается символом и принимает истинное
значение, когда высказывания различны по
значению.
3. Свойства двоичного сложения
x x 0x x 1
x 0 x
x 1 x
Коммутативность :
x y y x
Ассоциативность :
x y z x y z
Дистрибутивность :
x y z xz yz
4. Выражение основных логических операций через конъюнкцию и кольцевую сумму
x x 1x y x y xy
x y x xy 1
x y x y 1
5. Многочлен Жегалкина
формула над множеством функций , .Пример:
1 x xyz
y x xy
Теорема. Для любой булевой функции
существует задающий ее многочлен
Жегалкина. Он единственен с точностью
до перестановок слагаемых и порядка
переменных в конъюнкциях.
6. Методы получения многочлена Жегалкина
1. С помощью равносильныхпреобразований:
● заменить все логические связки через
кольцевую сумму и конъюнкцию;
● привести подобные слагаемые.
2. С помощью метода неопределенных
коэффициентов (МНК)
3. С помощью треугольника Паскаля
7. Пример
x y z yx y z y x y 1 z y
x y 1 1 z y x y z y
x y z x y z y x y z x z y z y
x y z 1 x z 1 y z 1 y
x y z 1 xz x yz y y
z 1 xz yz y z 1 xz yz z 1 xz yz y
1 z 1 xz yz zy y xyz yzy 1
z 1 xz yz zy y xyz yz 1
y z xz zy xyz.
8. Метод неопределенных коэффициентов
Для функции, зависящей от трехпеременных, в общем виде многочлен
Жегалкина имеет вид:
f 0 1 x 2 y 3 z 12 xy 23 yz 13 xz 123 xyz
С помощью таблицы истинности
подставляют в этот многочлен значения
переменных:
f 000 0 0;1
f 001 0 3 0;1 3 0;1 3 0;1
...
9. Пример
x y z yf 0 1 x 2 y 3 z 12 xy 23 yz 13 xz 123 xyz
f 000 0 0
f (001) a0 3 0 3 1 3 1
f (010) a0 2 0 2 1 2 1
f (100) a0 1 0 1 0 1 0
f (011) a0 2 3 23 0 1 1 23 1 23 1
f (101) a0 1 3 13 0 0 1 13 0 13 1
f (110) a0 1 2 12 0 0 1 12 1 12 0
f (111) a0 1 2 3 12 13 23 123
0 0 1 1 0 1 1 123 1 123 1
f y z yz xz xyz
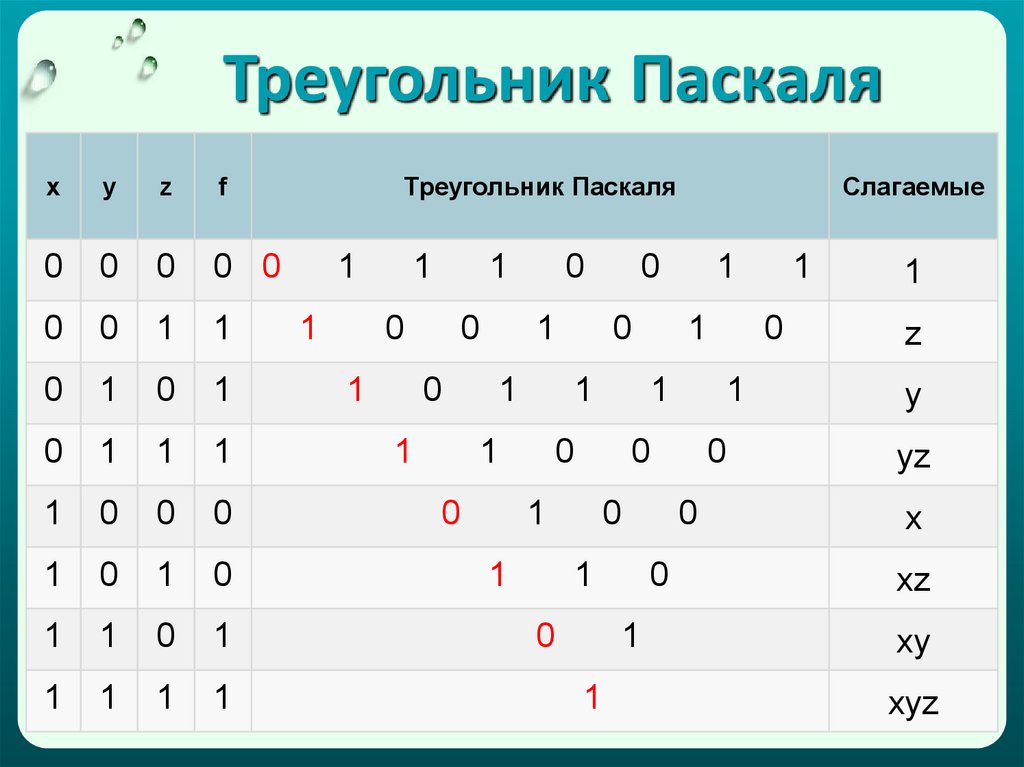
10. Треугольник Паскаля
xy
z
f
0
0
0
0 0
0
0
1
1
0
1
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
Треугольник Паскаля
1
1
1
1
0
1
0
1
0
1
0
1
0
0
1
1
1
1
1
1
0
0
0
1
Слагаемые
0
1
0
0
1
1
0
1
0
1
z
1
y
0
yz
x
xz
xy
xyz
11. Решение задач
Решить всеми тремя способами (равносильнымипреобразованиями, методом неопределенных
коэффициентов, треугольником Паскаля):
1. x y z x
y
z
x
y
2.
x
y
z
y
3.









 mathematics
mathematics








