Операция двоичного сложения и её свойства. Многочлен Жегалкина

1. Операция двоичного сложения и её свойства. Многочлен Жегалкина

2.

3.

4.

Диаграмма Венна для функции «Сложение по
модулю 2»

5.

Свойства операции сложение
по модулю 2
x1 x2 x2 x1
x1 ( x2 x3 ) ( x1 x2 ) x3
x1 ( x2 x3 ) x1 x2 x1 x3
x1 x2 x1 x2 x1 x2

6.

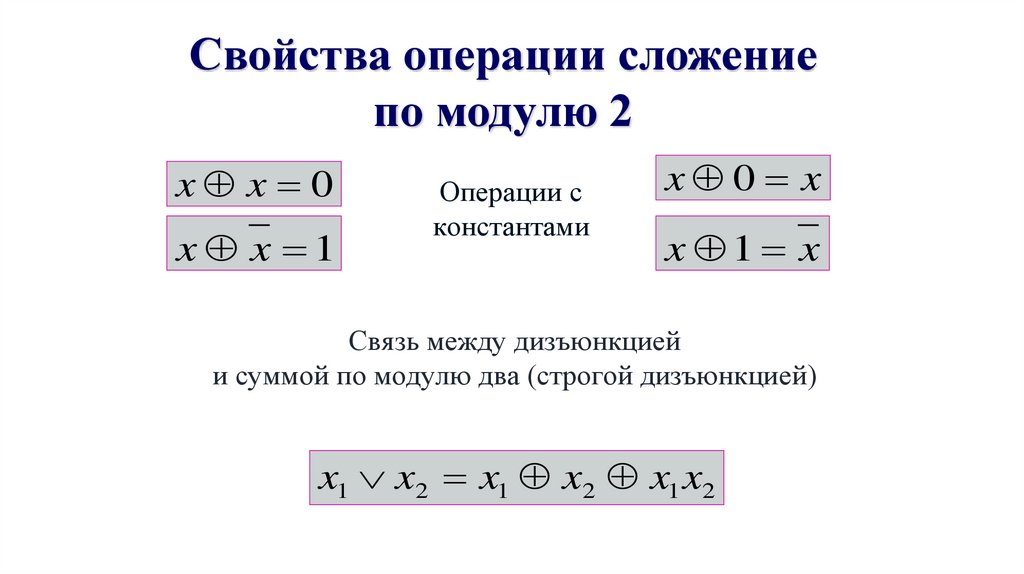
Свойства операции сложение
по модулю 2
x x 0
x x 1
Операции с
константами
x 0 x
x 1 x
Связь между дизъюнкцией
и суммой по модулю два (строгой дизъюнкцией)
x1 x2 x1 x2 x1 x2

7.

Многочленом Жегалкина называется альтернативная дизъюнкция конъюнкции
высказываний, самих высказываний и единицы

8.

Все функции алгебры логики можно выразить через многочленом
Жегалкина.

9.

Иван Иванович Жегалкин (1869-1947) – российский и советский математик и
логик, профессор Московского университета. Заслуженный деятель науки РСФСР
один из основоположников современной математической логики. Из его открытий
наибольшую известность получил так называемый полином Жегалкина. Жегалкин
награжден Орденом Трудового Красного Знамени.
Жегалкин предложил в 1927 году в качестве
удобного средства для представления функций
булевой логики многочлен, названный
полиномом Жегалкина.

10.

Этих шести формул достаточно, чтобы преобразовывать формулы
алгебры логики в многочлен Жегалкина.

11.

Пример.
Избавляемся от импликации применяя
формулу 4.
Раскрываем скобки и избавляемся от
инверсии, используя формулу 1.
Раскрываем скобки и используем
формулу 2.
Получили многочлен Жигалкина

12.

13.

Для двух переменных полином Жегалкина имеет вид:
Для каждой строчки таблицы истинности записываем выражение значение функции,
подставляя значения переменных х и у

14.

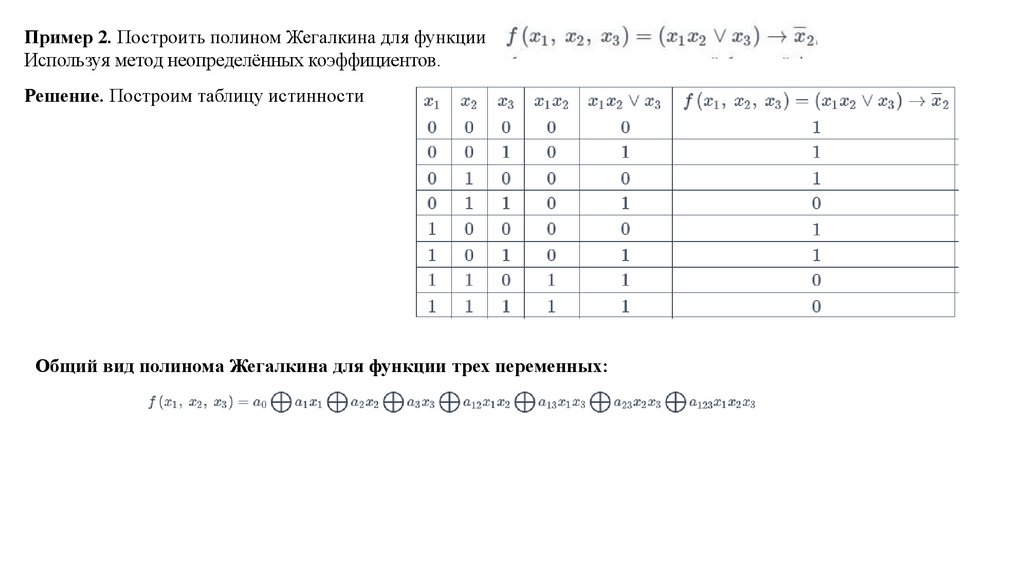
Пример 2. Построить полином Жегалкина для функции
Используя метод неопределённых коэффициентов.
Решение. Построим таблицу истинности
Общий вид полинома Жегалкина для функции трех переменных:

15.

Последовательно подставляем наборы значений переменных и находим коэффициенты
Подставляя найденные коэффициенты, получаем полином Жегалкина

16. Метод неопределенных коэффициентов (по таблице истинности или вектору значений функции)

xyz f
a0 a1 x a2 y a3 z a12 xy a13 xz a23 yz a123 xyz
0001 a
0011 a a 1 a
0100 a a 1 a
0110 a a a a 1 1 0 a
1001 a a 1 a
1010 a a a a 1 0 0 a
1101 a a a a 1 0 1 a
1111 a a a a a a a a 1 0 1 0 1 1 0 a
0
a0 1
0
3
3
a3 0
0
2
2
a2 1
0
0
a
2
3
23
0
1
0
1
3
13
0
1
2
12
1
23
1
2
3
12
13
12
13
23
123
123
P 1 y xy xz xyz
a23 0
a1 0
a13 1
a12 1
a123 1

17. Пример 1

x ∧ (y →z)
xyz f
0000 a
0010 0 a
0100 0 a
0110 0 0 0 a
1001 0 a
1011 0 1 0 a
1100 0 1 0 a
1111 0 1 0 0 1 0 0 a
0
a
a0 0
3
a3 0
2
a2 0
23
1
a23 0
a1 1
13
a13 0
12
a12 1
123
P x xy xyz
a123 1

18. Пример 2

xyz f
x ↓ (y | z)
0000 a
0010 0 a
0100 0 a
0111 0 0 0 a
1000 0 a
1010 0 0 0 a
1100 0 0 0 a
1110 0 0 0 0 0 0 1 a
0
a
a0 0
3
a3 0
2
a2 0
23
1
a23 1
a1 0
13
a13 0
12
a12 0
123
P yz xyz
a123 1

19. Пример 3

xyz f
0000
0011
0101
0110
1000
1010
1100
1110
x ↓ (y ↔ z)
a
a0
a0 0
0 a3
a3 1
0 a2
a2 1
0 1 1 a23
a23 0
0 a1
a1 0
0 0 1 a13
a13 1
0 0 1 a12
a12 1
0 0 1 1 1 1 0 a123
a123 0
P y z xy xz

20. Пример 4

x ∨ (y ↔ z)
xyz f
0001
0010
0100
0111
1001
1011
1101
1111
a
a0
a0 1
1 a3
a3 1
1 a2
a2 1
1 1 1 a23
a23 0
1 a1
a1 0
1 0 1 a13
a13 1
1 0 1 a12
a12 1
1 0 1 1 1 1 0 a123
a123 0
P 1 y z xy xz

21. Пример 5

xyz f
0001
0011
0101
0111
1000
1011
1101
1110
x | (y ↔ z)
a
a0
a0 1
1 a3
a3 0
1 a2
a2 0
1 0 0 a23
a23 0
1 a1
a1 1
1 1 0 a13
a13 1
1 1 0 a12
a12 1
1 1 0 0 1 1 0 a123
a123 0
P 1 x xy xz

22.

Дополнительное задание.
Пусть функция задана вектором значений
f = (11001011).
Найти полином Жегалкина.