Similar presentations:
Логические основы ЭВМ
1.
2.
Логика – наука о законах мышления и его формах. Происходит от греческогослова логос – речь. Основой логики служит высказывание.
Родоначальник – Аристотель (IV век до н. э) – появление формальной логики
– рассуждения.
Последователь – Лейбниц (XVII век) – появление математической
(символической) логики.
Основоположник – Джордж Буль (XIX век) – появление математической
логики, как самостоятельной науки (булева алгебра).
В 1938 году появилась статья Клода Шеннона “Символический анализ
релейно-контактных схем”, где он впервые применил логику.
Аристотель
Лейбниц Готфрид
Вильгельм
Джордж Буль
Шеннон Клод Элвуд
3.
Понятие – это форма мышления, фиксирующая основные, существенныепризнаки объекта.
Высказывание – это форма мышления, в которой что-либо утверждается или
отрицается о свойствах реальных предметов и отношениях между ними.
Высказывание может быть либо истинно, либо ложно.
Умозаключение – это форма мышления, с помощью которой из одного или
нескольких суждений (посылок) может быть получено новое суждение
(заключение)
Высказывания
Простые
Составные
Получаются из простых с
использованием логических
операций или союзов “и”, “или”,
“не”, “если то”.
4. Простейшие логические операции
1.2.
3.
4.
5.
6.
7.
Отрицание
Конъюнкция
Дизъюнкция
Импликация
Эквивалентность
Штрих Шеффера
Стрелка Пирса
5.
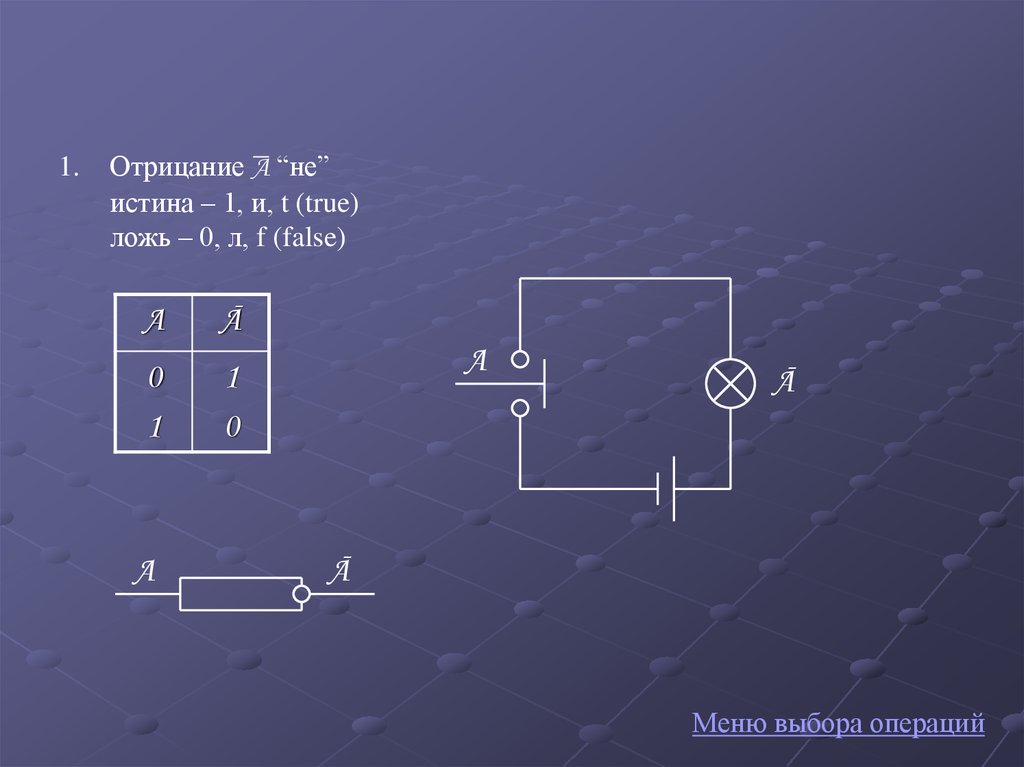
1.Отрицание А “не”
истина – 1, и, t (true)
ложь – 0, л, f (false)
A
Ā
0
1
1
0
A
A
Ā
Ā
Меню выбора операций
6.
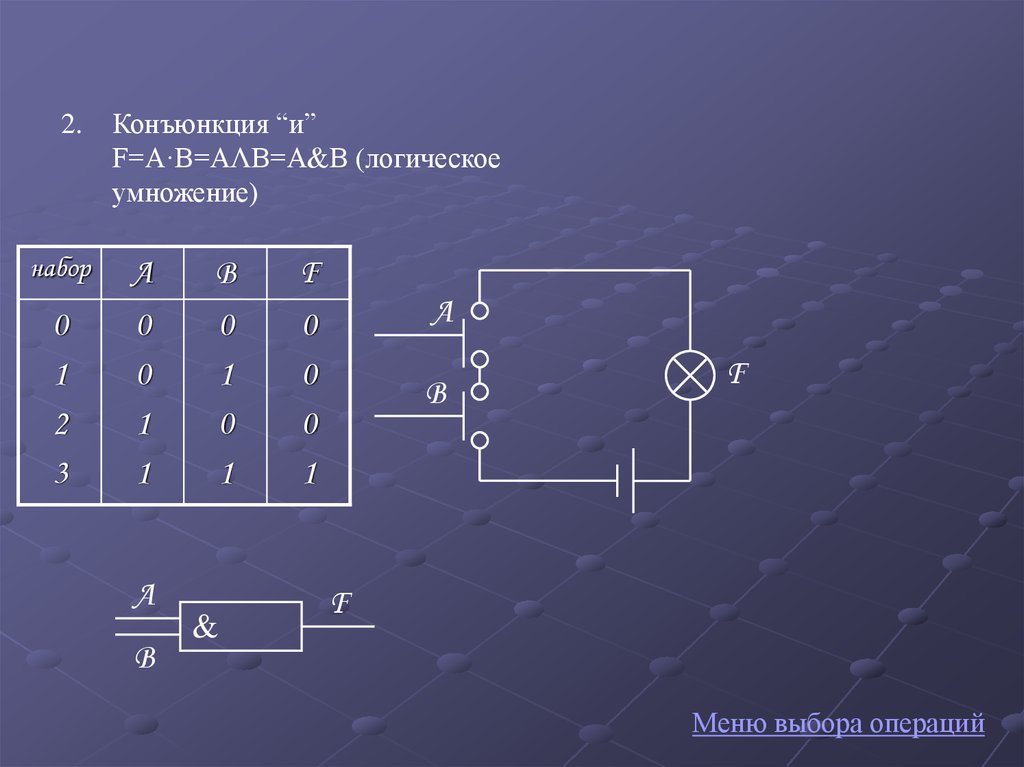
2.Конъюнкция “и”
F=A·B=AΛB=A&B (логическое
умножение)
набор
A
B
F
0
1
2
3
0
0
1
1
0
1
0
1
0
0
0
1
A
B
&
A
B
F
F
Меню выбора операций
7.
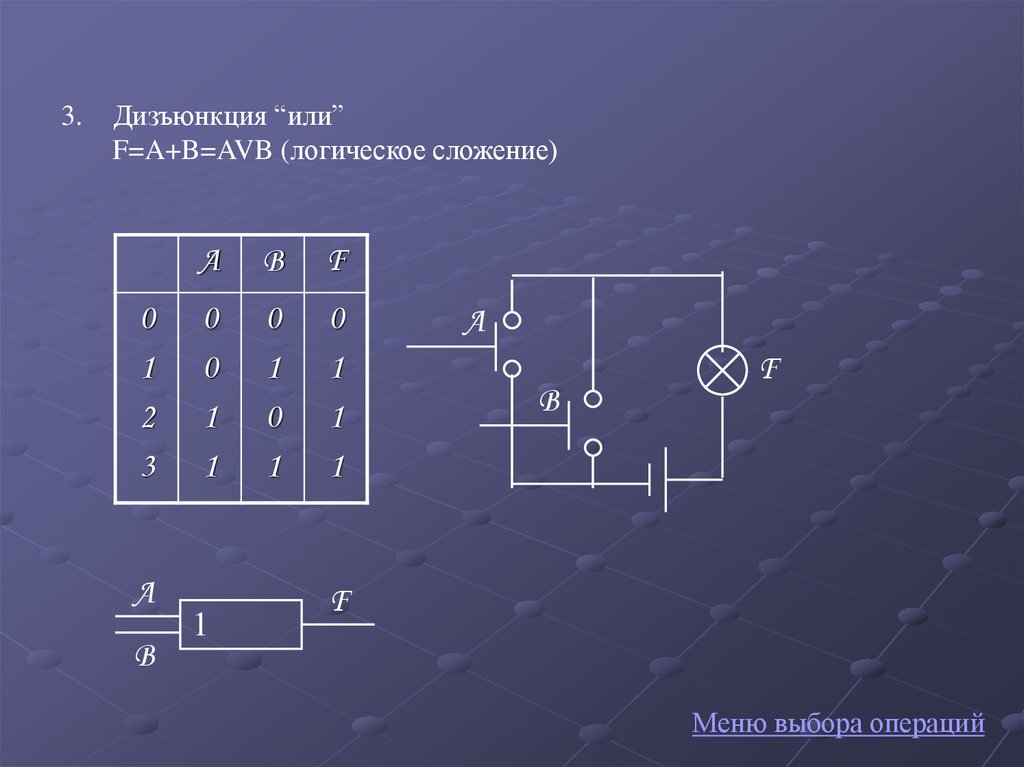
3.Дизъюнкция “или”
F=A+B=AVB (логическое сложение)
0
1
2
3
A
B
F
0
0
1
1
0
1
0
1
0
1
1
1
A
B
1
A
B
F
F
Меню выбора операций
8.
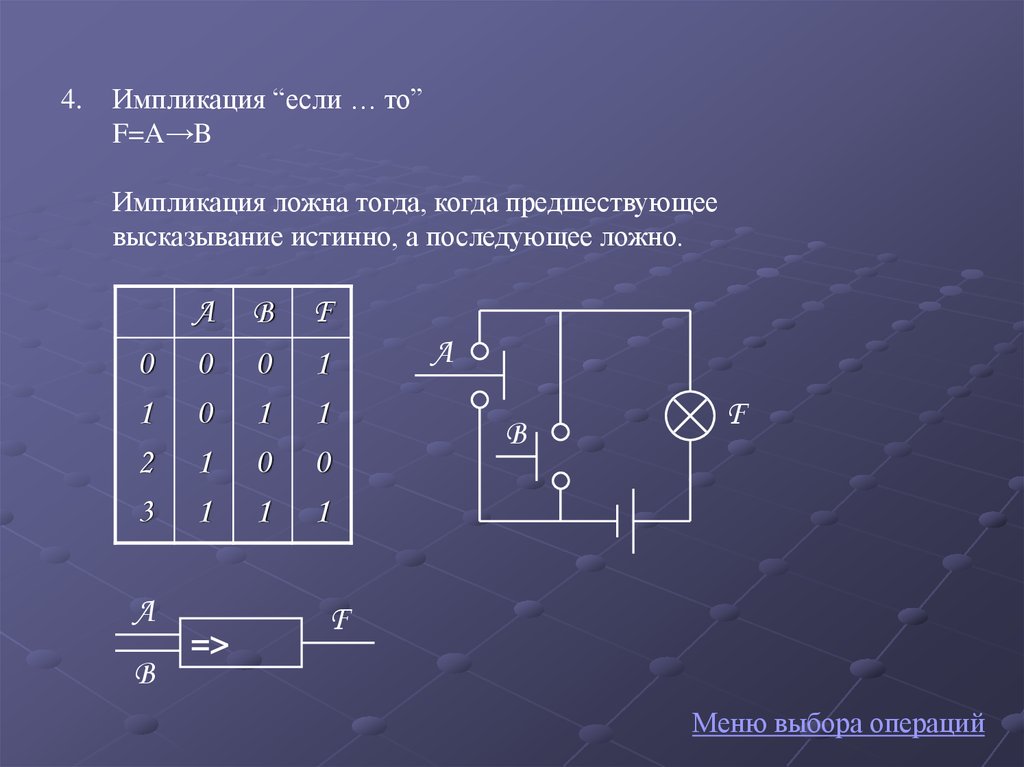
4.Импликация “если … то”
F=A→B
Импликация ложна тогда, когда предшествующее
высказывание истинно, а последующее ложно.
0
1
2
3
A
0
0
1
1
A
B
=>
B
0
1
0
1
F
1
1
0
1
A
B
F
F
Меню выбора операций
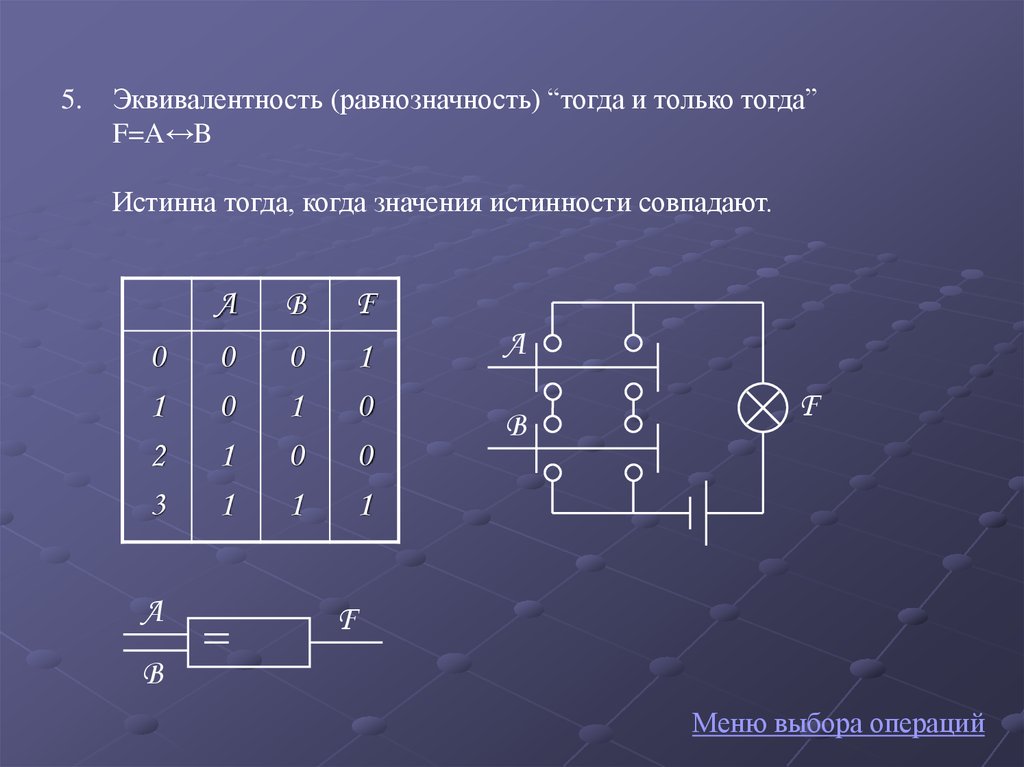
9.
5.Эквивалентность (равнозначность) “тогда и только тогда”
F=A↔B
Истинна тогда, когда значения истинности совпадают.
0
1
2
3
A
A
B
F
0
0
1
1
0
1
0
1
1
0
0
1
A
B
F
F
B
Меню выбора операций
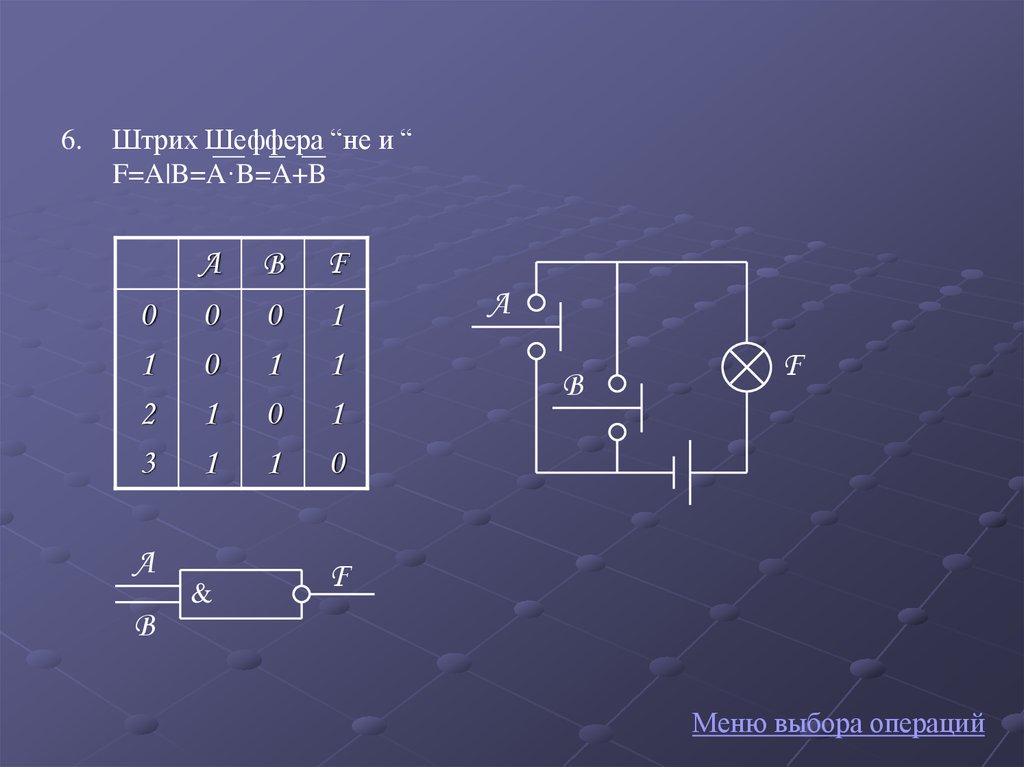
10.
6.Штрих Шеффера “не и “
F=A|B=A·B=A+B
0
1
2
3
A
0
0
1
1
A
B
&
B
0
1
0
1
F
1
1
1
0
A
B
F
F
Меню выбора операций
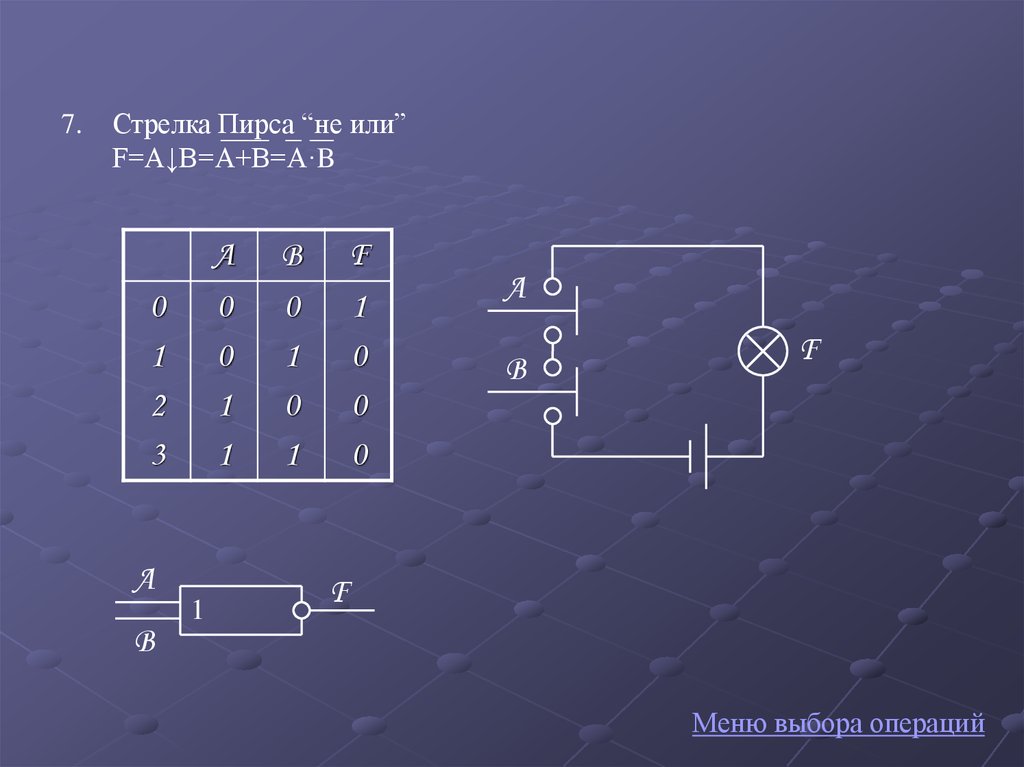
11.
7.Стрелка Пирса “не или”
F=A↓B=A+B=A·B
0
1
2
3
A
B
1
A
B
F
0
0
1
1
0
1
0
1
1
0
0
0
A
B
F
F
Меню выбора операций
12. Законы логики
I.x≡x
закон тождества
II.
x·x=0
закон противоречия
III.
x+x=1
закон исключения третьего
IV.
=x = x
закон двойного отрицания
V.
x·x=x
x+x=x
закон идемпотентности
VI.
x·y=y·x
x+y=y+x
закон переместительный или
коммутативный
VII.
x·y·z=x·(y·z)
x+y+z=x+(y+z)
закон сочетательный или
ассоциативный
VIII. x · ( y +z ) = x · y + x · z
x + ( y · z) = ( x + y ) ( x + z )
IX.
x·y=x+y
x+y=x·y
закон распределительный или
дистрибутивный
закон Моргана
13. Следствия из законов
1.x·1=x
x+0=x
2.
x·0=0
x+1=1
3.
x(x+y)=x
x+x·y=x
поглощение
4.
( x + y ) ( x + y) = y
x·y+x·y=y
склеивание
5.
x+x·y=x+y
x+x·y=x+y
свертка
14.
Составление таблиц истинностипо логическим формулам
F x y xy
2-ой способ
F(0;0) 0 0 0 0 0 1 1 0 0
1-ый способ
F(0;1) 0 1 0 1 0 0 1 1 1
x
y
x
y
0 0 1 1
xy xy F
0
0 0
0 1 1 0
0
1 1
1 0 0 1
1
0 1
1 1 0 0
0
0 0
F(1;0) 1 0 1 0 1 1 0 0 1
F(1;1) 1 1 1 1 1 0 0 1 0
x
0
0
1
1
y
0
1
0
1
F
0
1
1
0
15.
Составление формул позаданным таблицам истинности
Получение совершенно нормальной дизъюнктивной формы (СНДФ)
Получение совершенной нормальной конъюнктивной формы (СНКФ)
16.
Получение совершенно нормальнойдизъюнктивной формы (СНДФ)
F x y z x y z xyz
y z (x x ) xyz
1
xyz y z xyz y z
стрелка
Пирса
&
1
x y z
1
F
x
y
z
F
0
0
0
0
1
1
0
0
1
0
2
0
1
0
0
3
0
1
1
0
4
1
0
0
1
5
1
0
1
0
6
1
1
0
0
7
1
1
1
1
x y z
x y z
xyz
F ( 0; 4 ;7 ) = 1
Составление формул по заданным таблицам истинности
17.
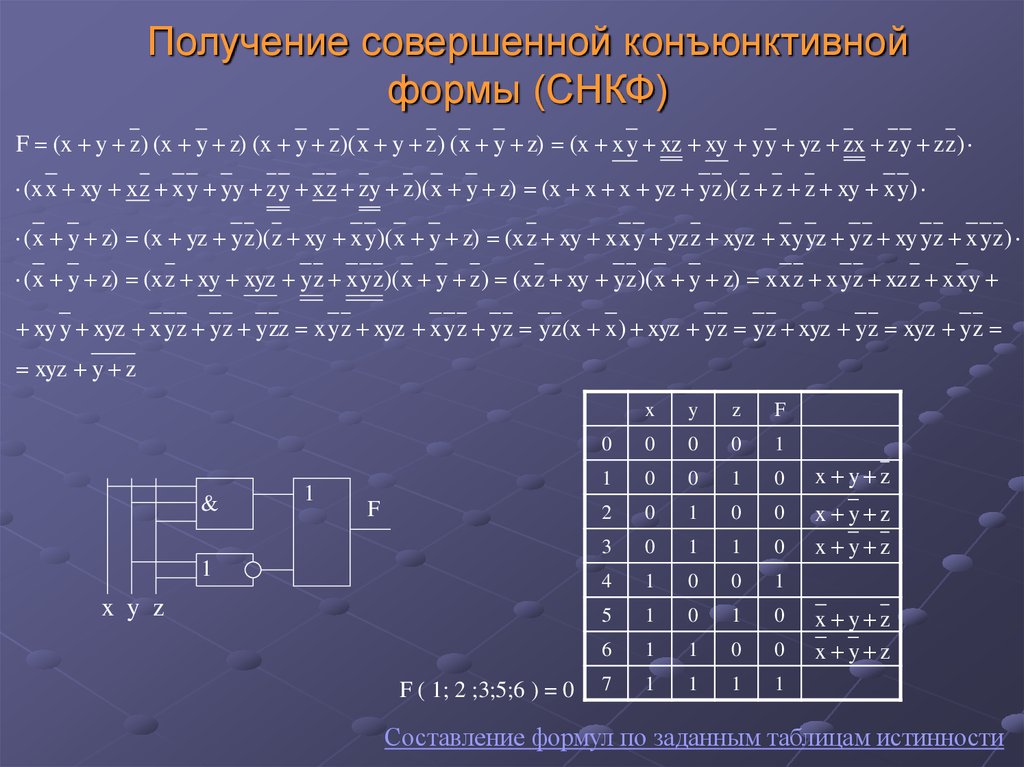
Получение совершенной конъюнктивнойформы (СНКФ)
F (x y z) (x y z) (x y z)( x y z) ( x y z) (x x y xz xy y y yz zx z y z z)
(x x xy x z x y yy z y x z zy z)( x y z) (x x x yz y z)( z z z xy x y)
( x y z) (x yz y z)( z xy x y)( x y z) (x z xy x x y yz z xyz xy yz y z xy y z x yz)
( x y z) (x z xy xyz y z x y z)( x y z) (x z xy y z)( x y z) x x z x y z xz z x xy
xy y xyz x y z yz yzz x y z xyz x y z y z yz(x x ) xyz yz yz xyz y z xyz yz
xyz y z
&
1
F
1
x y z
F ( 1; 2 ;3;5;6 ) = 0
x
y
z
F
0
0
0
0
1
1
0
0
1
0
2
0
1
0
0
3
0
1
1
0
4
1
0
0
1
5
1
0
1
0
6
1
1
0
0
7
1
1
1
1
x y z
x y z
x y z
x y z
x y z
Составление формул по заданным таблицам истинности
18.
Схема одноразрядного сумматораP xy
Z xy x y xy x y x x y y
x (x y) y(x y) (x y)( x y) (x y)( xy )
&
P
&
1
x y
Z
x
y
p
Z
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
19. Задача
Судейская коллегия, состоящая из 3 человек, выносит решениебольшинством голосов. Построить логическую схему, реализующую данное
утверждение.
" Да"-1
x
y
z
F
" Нет"-0
0
0
0
0
0
F (3;5;6;7) 1
1
0
0
1
0
F xyz x yz xy z xyz xyz x yz xy (z z)
011
101
110
111
2
0
1
0
0
3
0
1
1
1
xyz x yz xy xyz x (y yz)
4
1
0
0
0
xyz x (y z) xyz xy xz z (x xy) xy
5
1
0
1
1
6
1
1
0
1
&
7
1
1
1
1
&
1
z (x y) xy xy xz yz
&
x y z
1
F











 informatics
informatics








