Similar presentations:
Вектор, длина (модуль) вектора, сонаправленные векторы, противоположно направленные векторы, коллинеарность векторов
1.
Вектор, длина (модуль) вектора,сонаправленные векторы,
противоположно направленные
векторы, коллинеарность векторов,
равенство векторов Определение
векторов. Физический и
геометрический смысл векторов.
2.
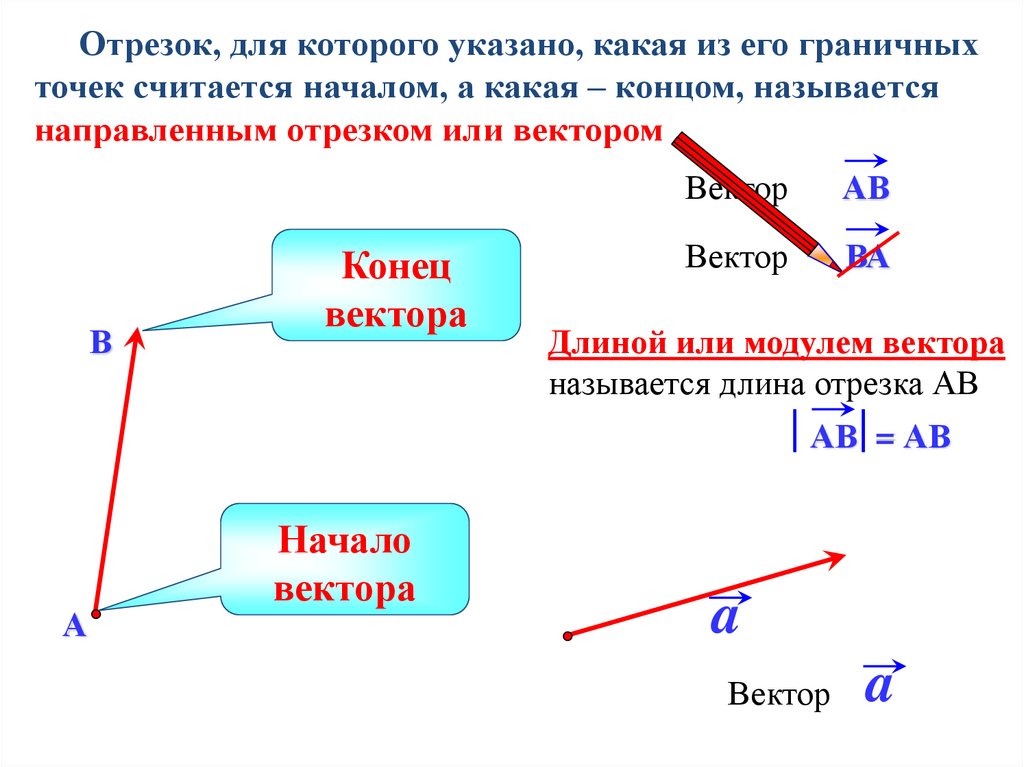
Отрезок, для которого указано, какая из его граничныхточек считается началом, а какая – концом, называется
направленным отрезком или вектором
В
Конец
вектора
Вектор
АВ
Вектор
ВА
Длиной или модулем вектора
называется длина отрезка АВ
АВ = АВ
А
Начало
вектора
a
Вектор
a
3.
Любая точка плоскости также является вектором.В этом случае вектор называется нулевым
Вектор
MM
Вектор
0
M
Начало нулевого вектора совпадает с его концом,
поэтому нулевой вектор не имеет какого-либо
определенного направления. Иначе говоря, любое
направление можно считать направлением нулевого
вектора.
Длина нулевого считается равной нулю
MM = 0
4.
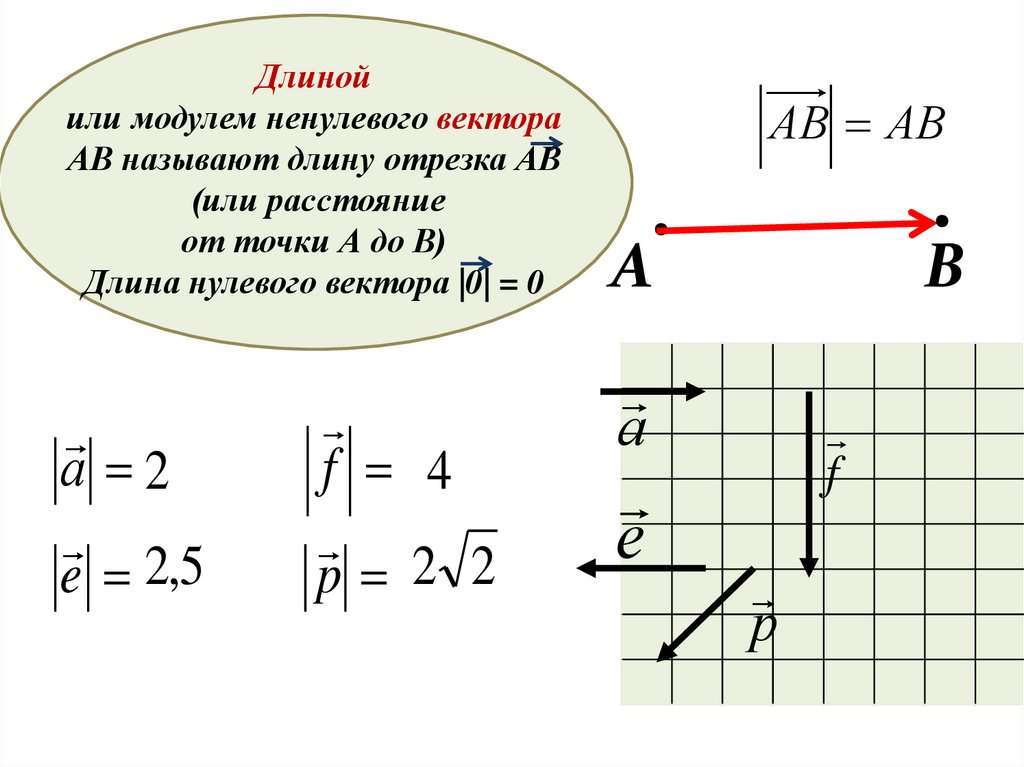
Длинойили модулем ненулевого вектора
АВ называют длину отрезка АВ
(или расстояние
от точки А до В)
Длина нулевого вектора |0| = 0
а 2
2,5
e
f 4
2 2
p
АВ АВ
A
B
а
е
f
р
5.
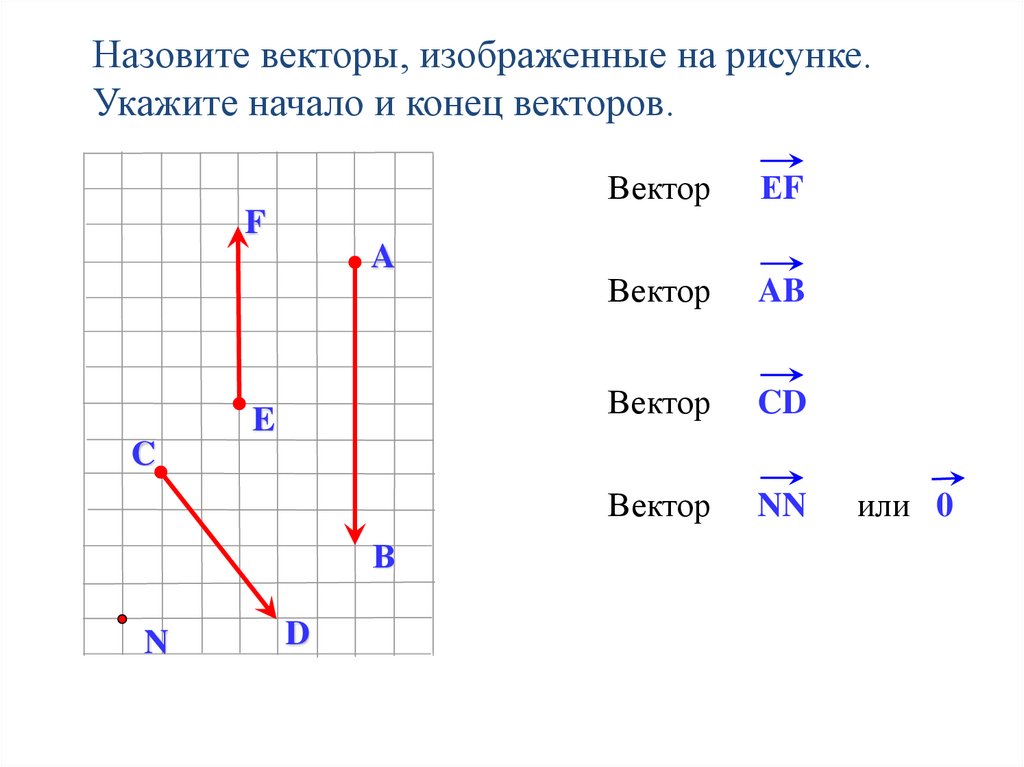
Назовите векторы, изображенные на рисунке.Укажите начало и конец векторов.
Вектор
ЕF
Вектор
AB
Вектор
CD
Вектор
NN
F
A
E
C
В
N
D
или 0
6.
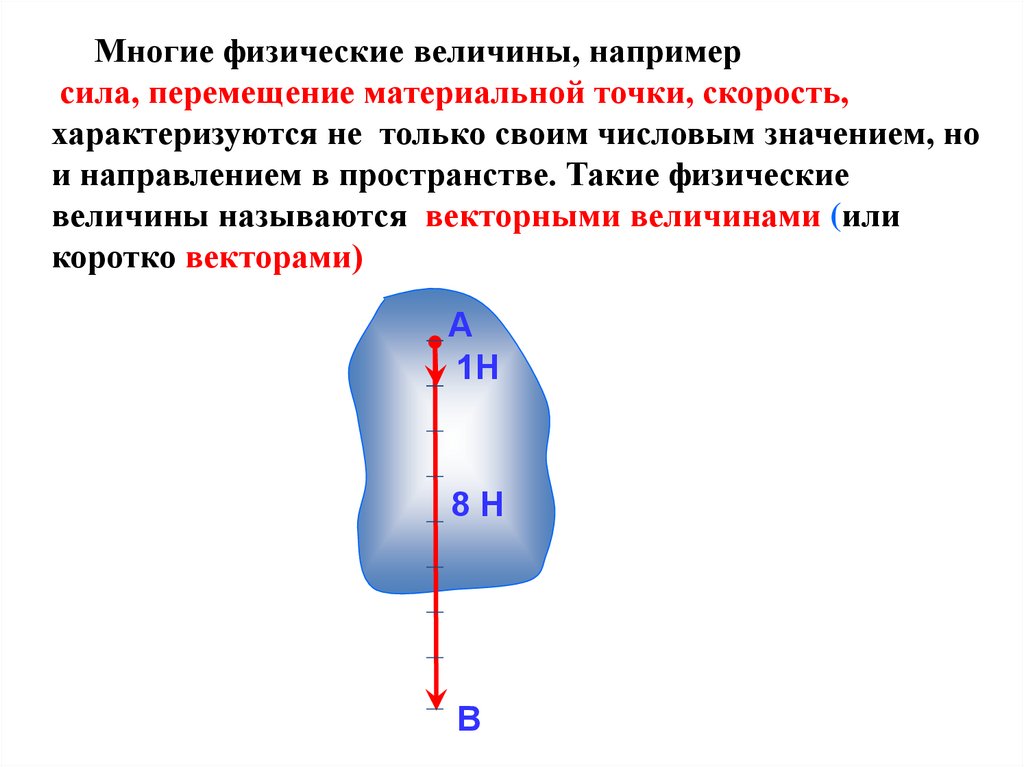
Многие физические величины, напримерсила, перемещение материальной точки, скорость,
характеризуются не только своим числовым значением, но
и направлением в пространстве. Такие физические
величины называются векторными величинами (или
коротко векторами)
A
1Н
8Н
В
7.
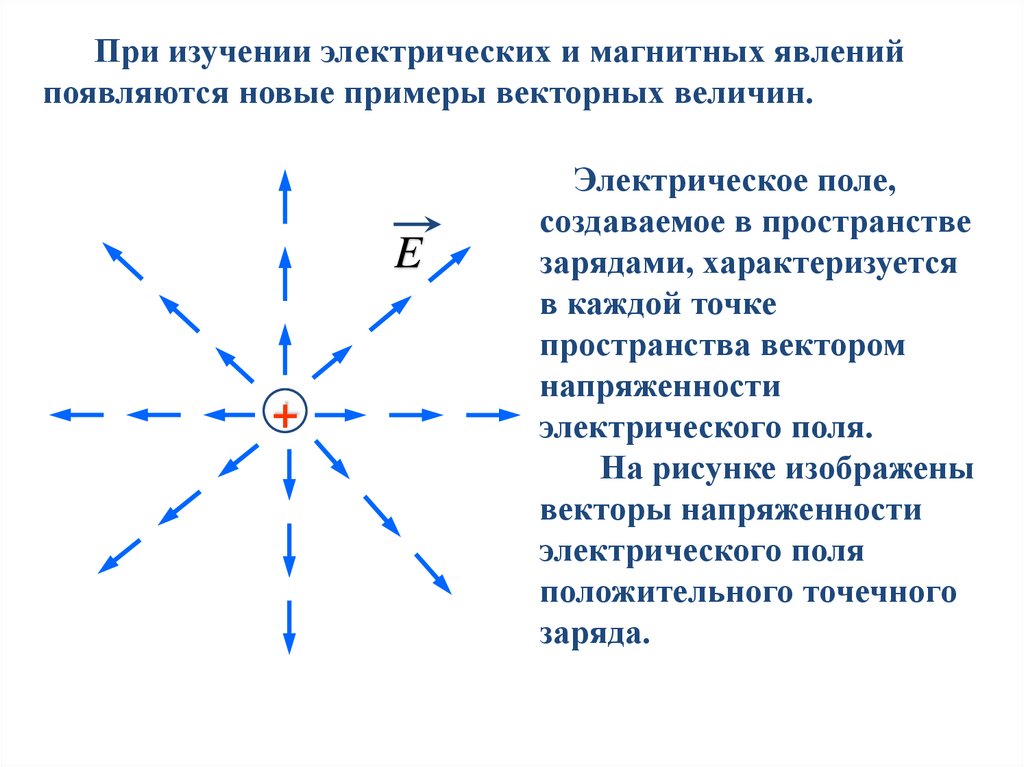
При изучении электрических и магнитных явленийпоявляются новые примеры векторных величин.
E
+
Электрическое поле,
создаваемое в пространстве
зарядами, характеризуется
в каждой точке
пространства вектором
напряженности
электрического поля.
На рисунке изображены
векторы напряженности
электрического поля
положительного точечного
заряда.
8.
Направление токаB
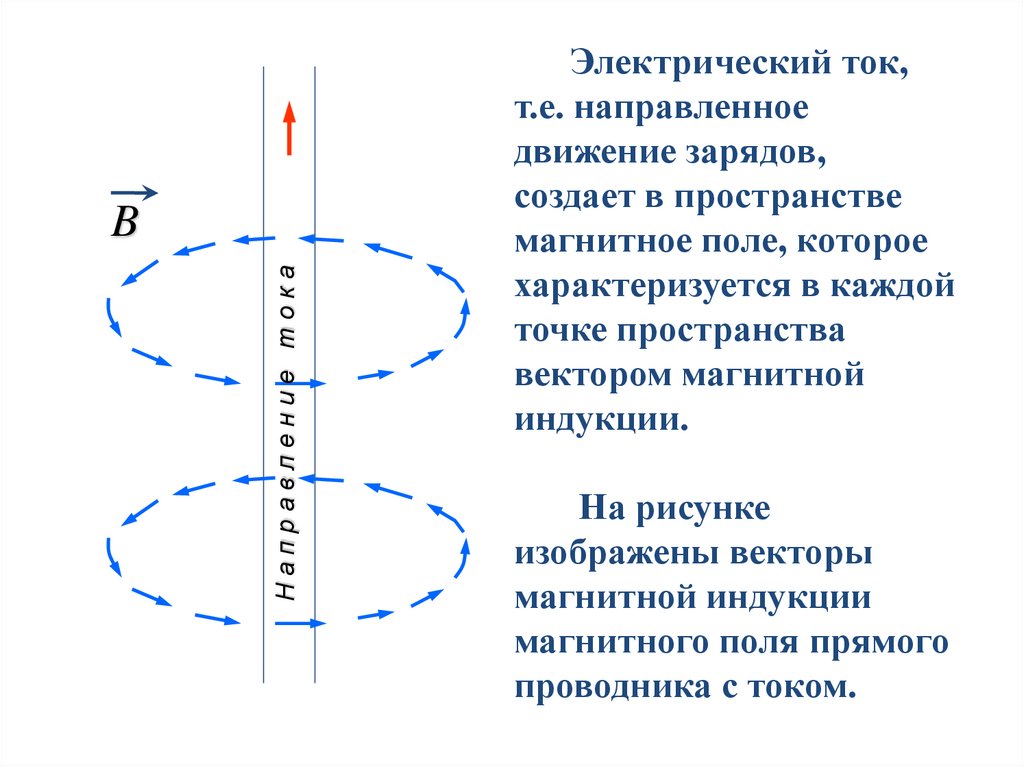
Электрический ток,
т.е. направленное
движение зарядов,
создает в пространстве
магнитное поле, которое
характеризуется в каждой
точке пространства
вектором магнитной
индукции.
На рисунке
изображены векторы
магнитной индукции
магнитного поля прямого
проводника с током.
9.
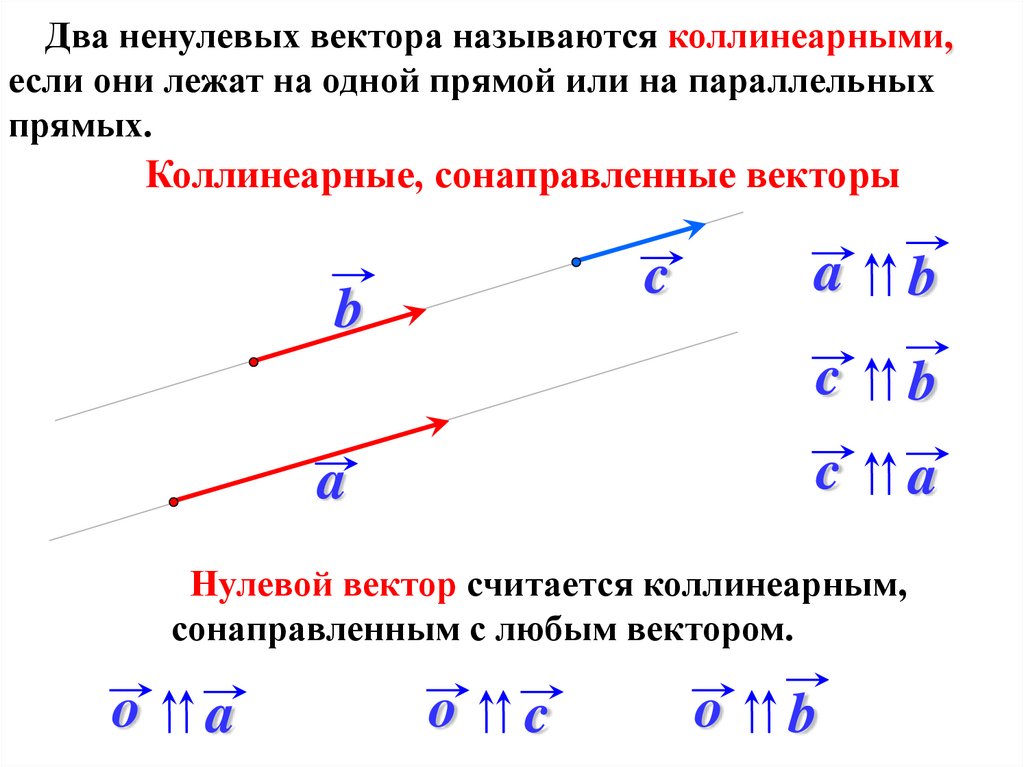
Два ненулевых вектора называются коллинеарными,если они лежат на одной прямой или на параллельных
прямых.
Коллинеарные, сонаправленные векторы
c
b
a
a
b
c
b
c
a
Нулевой вектор считается коллинеарным,
сонаправленным с любым вектором.
o
a
o
c
o
b
10.
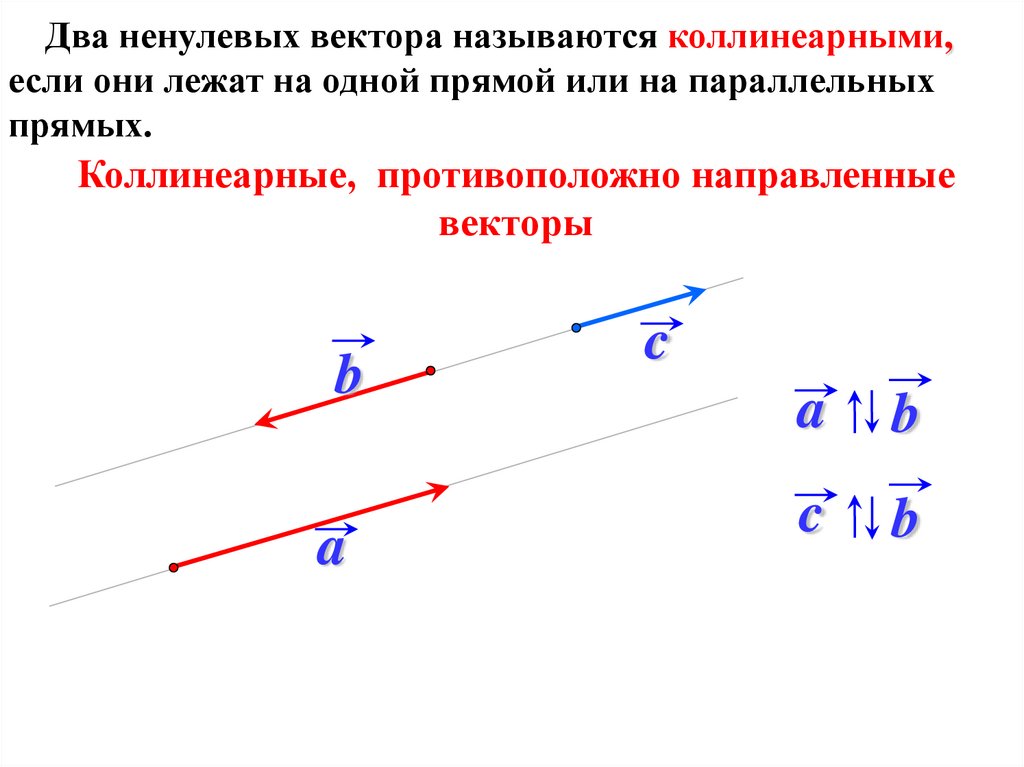
Два ненулевых вектора называются коллинеарными,если они лежат на одной прямой или на параллельных
прямых.
Коллинеарные, противоположно направленные
векторы
b
a
c
a
b
c
b
11.
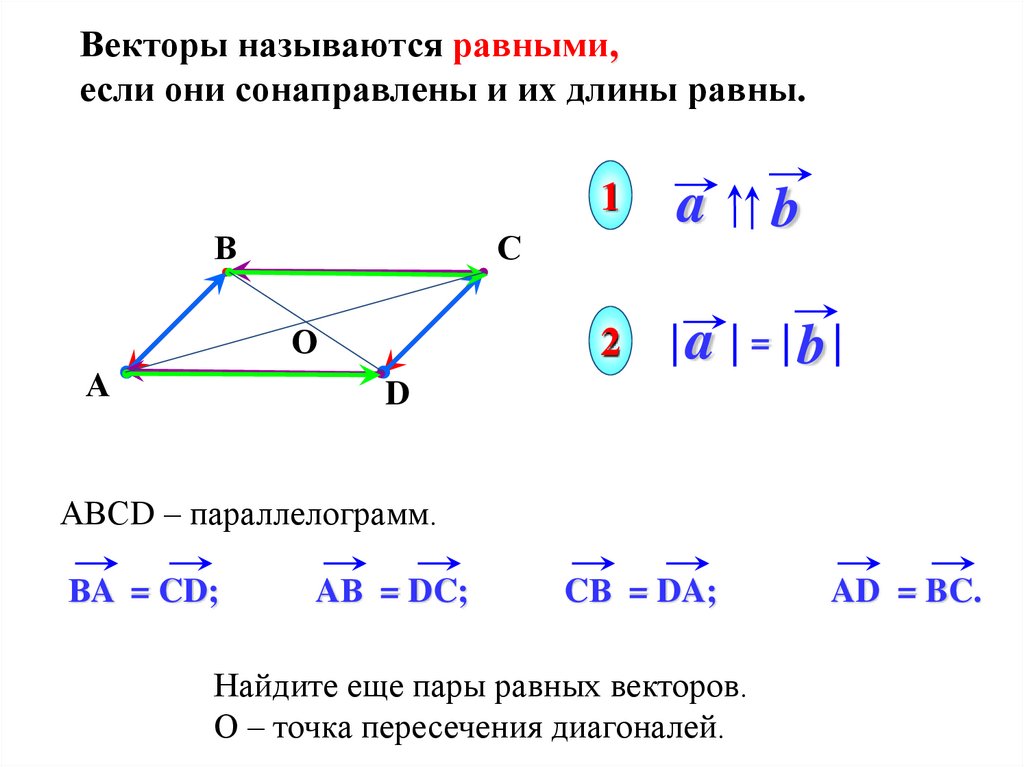
Векторы называются равными,если они сонаправлены и их длины равны.
В
a
2
a = b
С
О
А
1
b
D
АВСD – параллелограмм.
ВA = CD;
AВ = DC;
CВ = DA;
Найдите еще пары равных векторов.
О – точка пересечения диагоналей.
AD = BC.
12.
еа
f
с
а с , так как ...
а е , так как ...
а f , так как ...
a с u а с
а е
a f и векторы а и f
не сонаправлены
ВЕКТОРЫ
НАЗЫВАЮТСЯ
РАВНЫМИ,
ЕСЛИ ОНИ
СОНАПРАВЛЕНЫ И
ИХ ДЛИНЫ
ОДИНАКОВЫ.
13.
ВА
С
D
14.
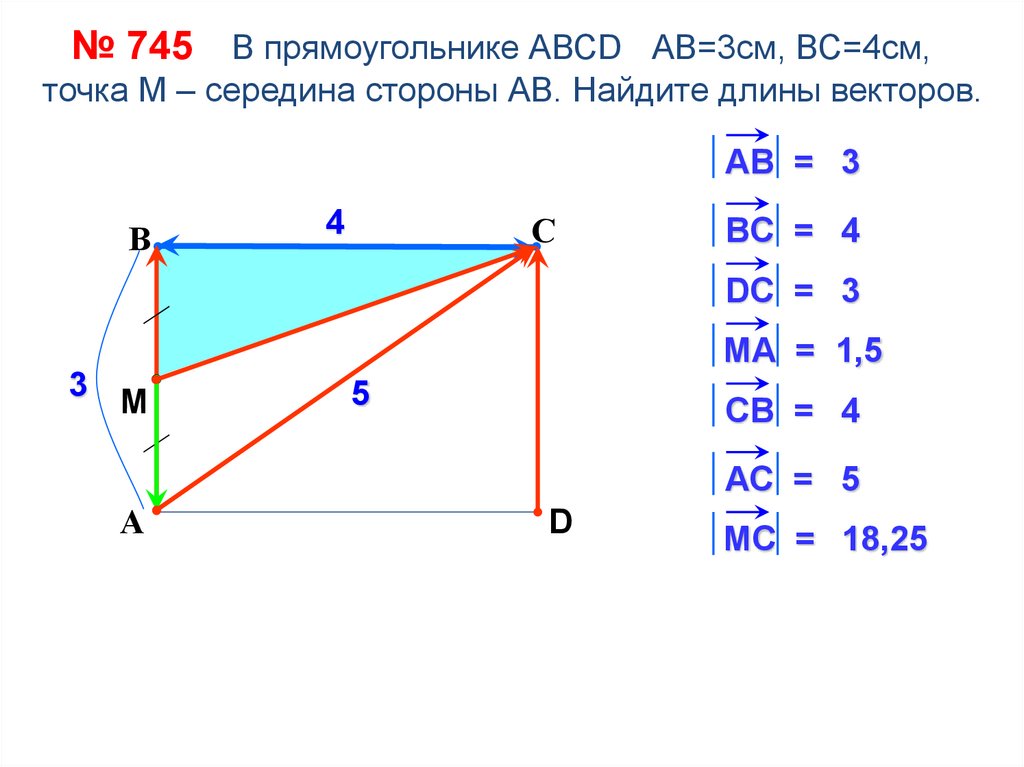
№ 745 В прямоугольнике АВСD АВ=3см, ВС=4см,точка М – середина стороны АВ. Найдите длины векторов.
АВ = 3
В
4
С
ВC = 4
DС = 3
MА = 1,5
3 M
5
СВ = 4
АС = 5
А
D
МC = 18,25
15.
№ 747 Укажите пары коллинеарных(сонаправленных) векторов, которые определяются
сторонами параллелограмма MNPQ.
P
N
M
MN
Q
QP
NM
PQ
QM
PN
MQ
NP
16.
№ 747 Укажите пары коллинеарных(противоположно направленных) векторов, которые
определяются сторонами параллелограмма MNPQ.
P
N
M
MN
Q
PQ
NM
QP
MQ
PN
QM
NP
17.
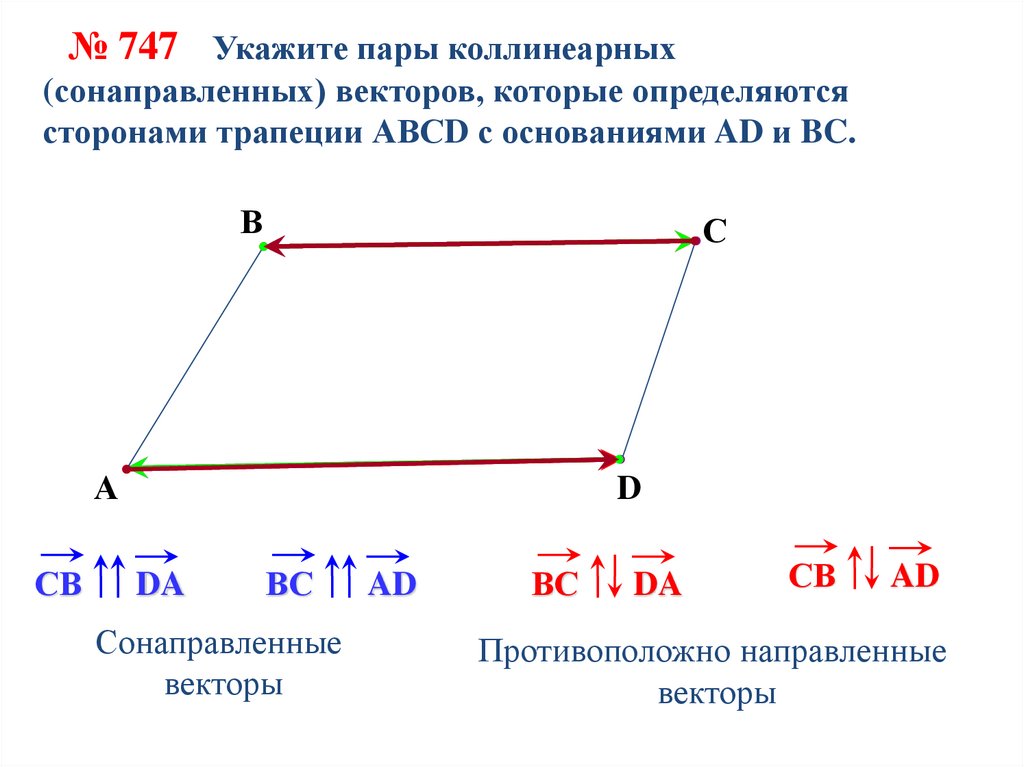
№ 747 Укажите пары коллинеарных(сонаправленных) векторов, которые определяются
сторонами трапеции АВСD с основаниями AD и BC.
В
С
А
СВ
D
DA
ВС
Сонаправленные
векторы
AD
ВС
DA
СВ
AD
Противоположно направленные
векторы
18.
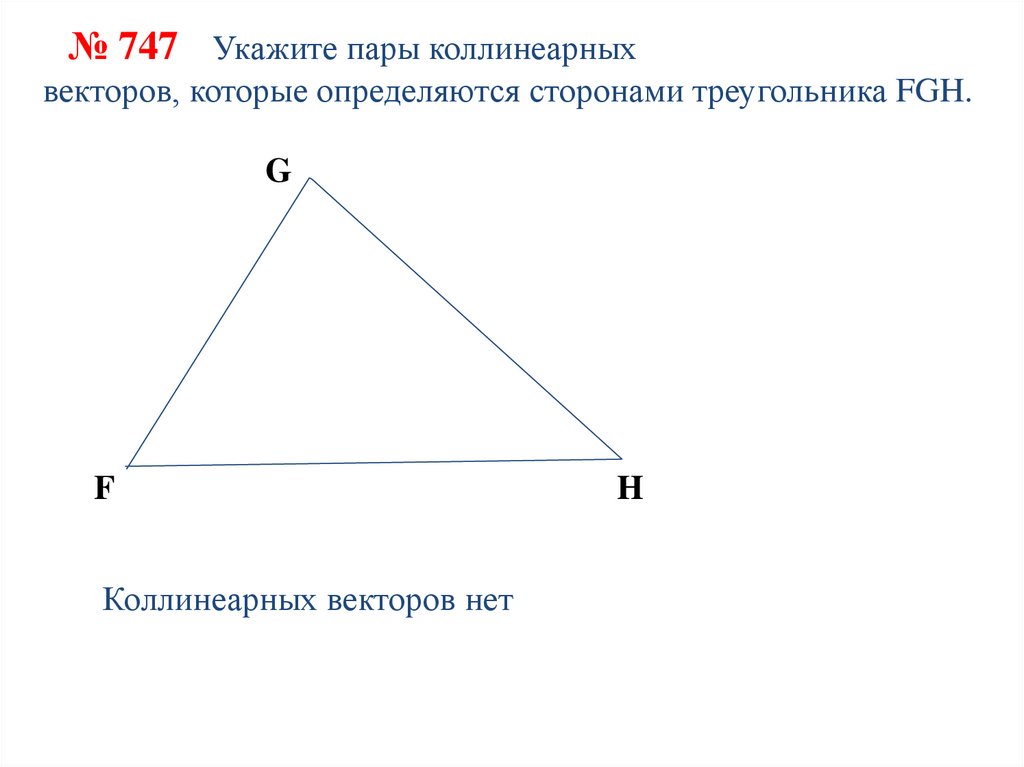
№ 747 Укажите пары коллинеарныхвекторов, которые определяются сторонами треугольника FGH.
G
F
Коллинеарных векторов нет
H
19.
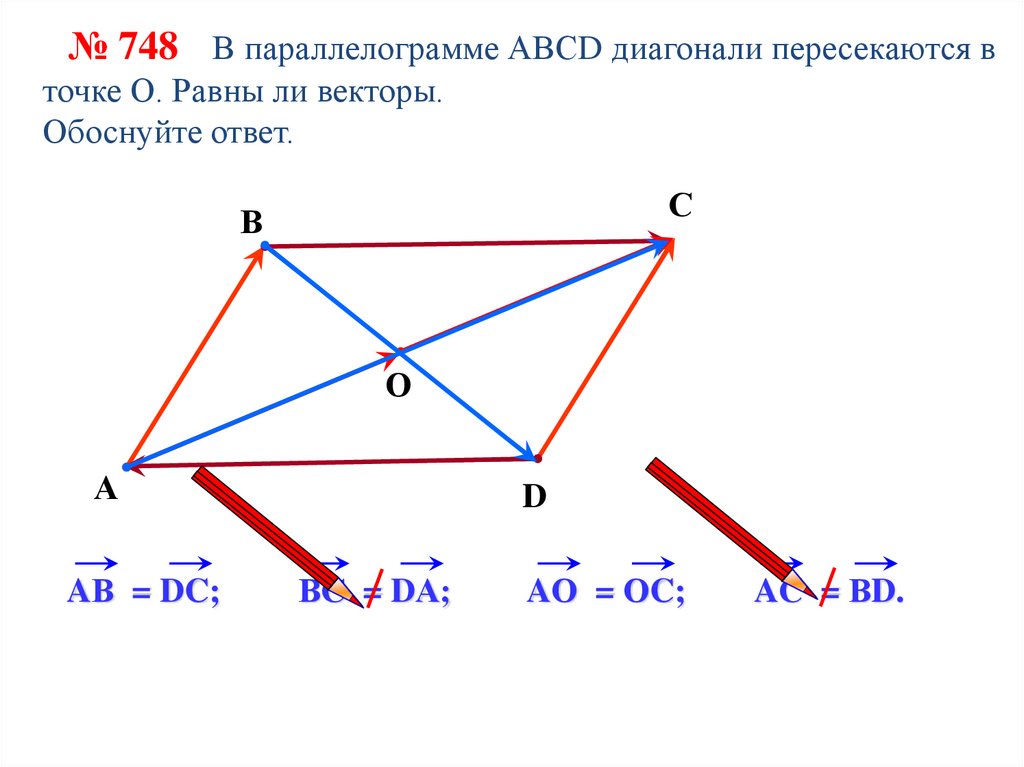
№ 748 В параллелограмме АВСD диагонали пересекаются вточке О. Равны ли векторы.
Обоснуйте ответ.
С
В
О
А
AВ = DC;
D
ВС = DА;
AО = ОC;
AС = ВD.
20.
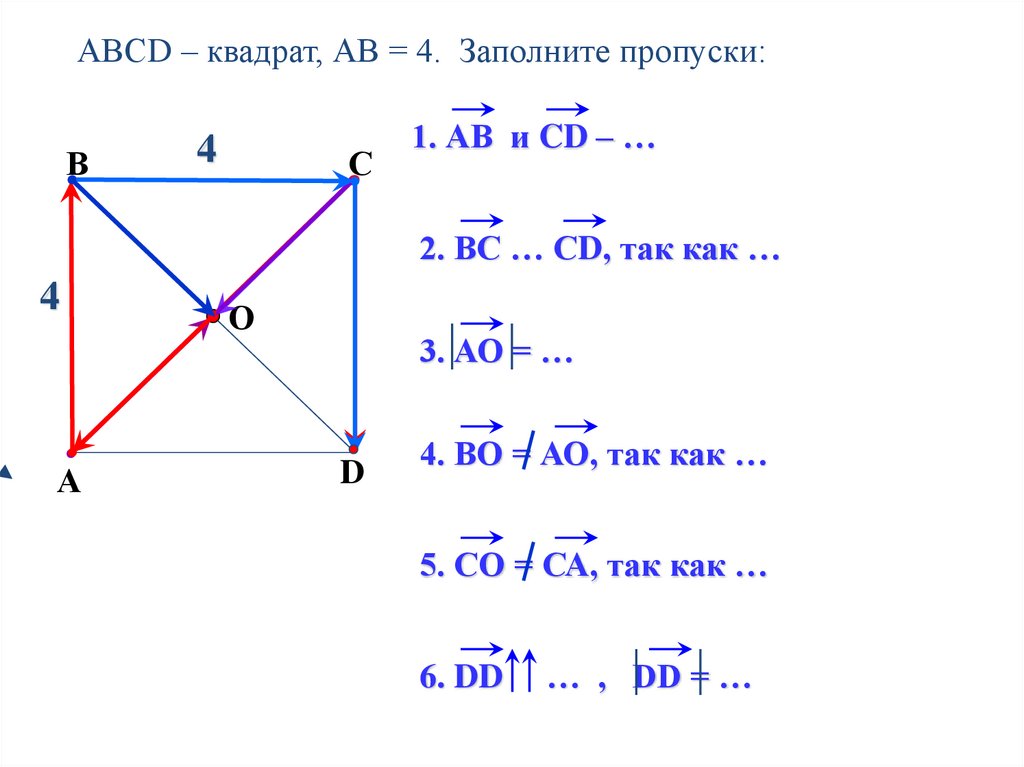
АВСD – квадрат, АВ = 4. Заполните пропуски:В
4
С
1. АВ и CD – …
2. ВС … СD, так как …
4
А
О
3. АО = …
D
4. ВО = АО, так как …
5. СО = СА, так как …
6. DD
… , DD = …
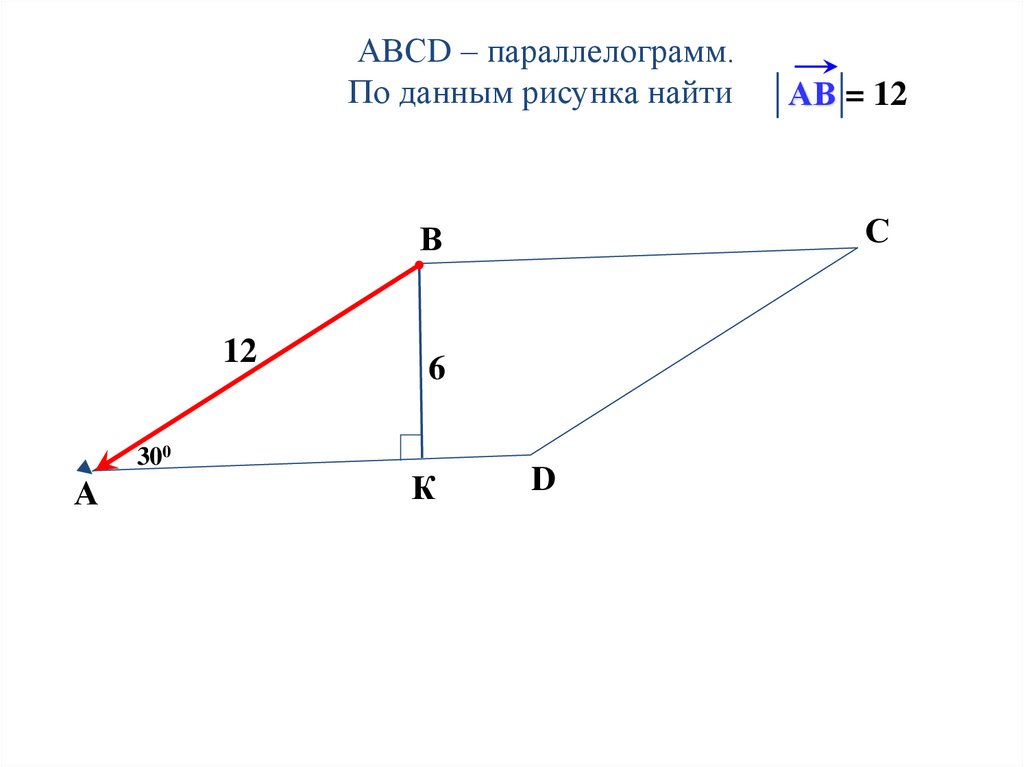
21.
АВСD – параллелограмм.По данным рисунка найти
С
В
12
300
А
6
К
АВ = 12
D
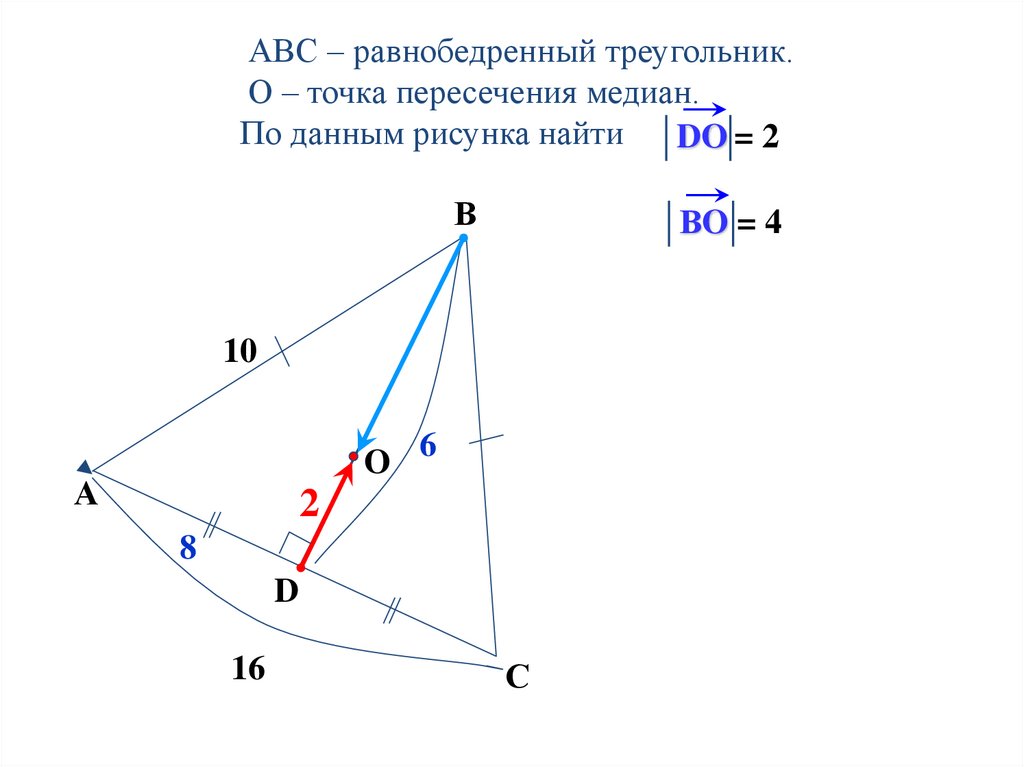
22.
АВС – равнобедренный треугольник.О – точка пересечения медиан.
По данным рисунка найти
DO = 2
В
ВO = 4
10
O 6
А
2
8
D
16
С
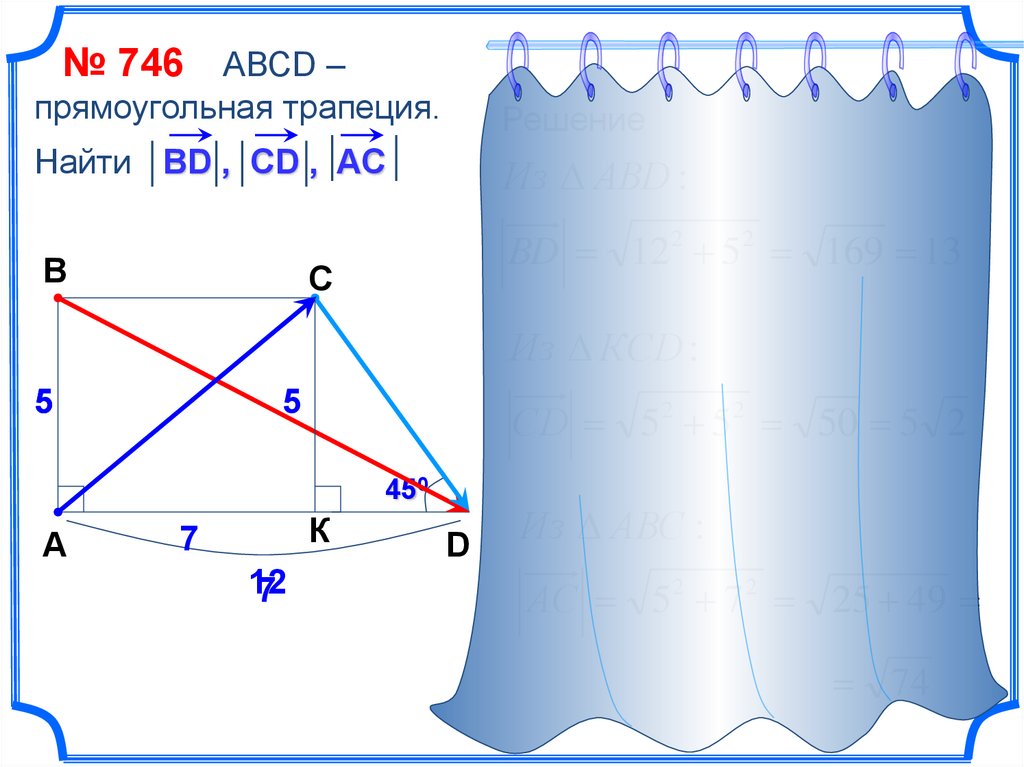
23.
№ 746 АВСD –прямоугольная трапеция.
Решение
Найти ВD , CD , AC
Из АВD :
B
BD 122 52 169 13
C
Из КСD :
5
5
СD 52 52 50 5 2
450
A
К
7
12
7
D
Из АВС :
АС 52 7 2 25 49
74
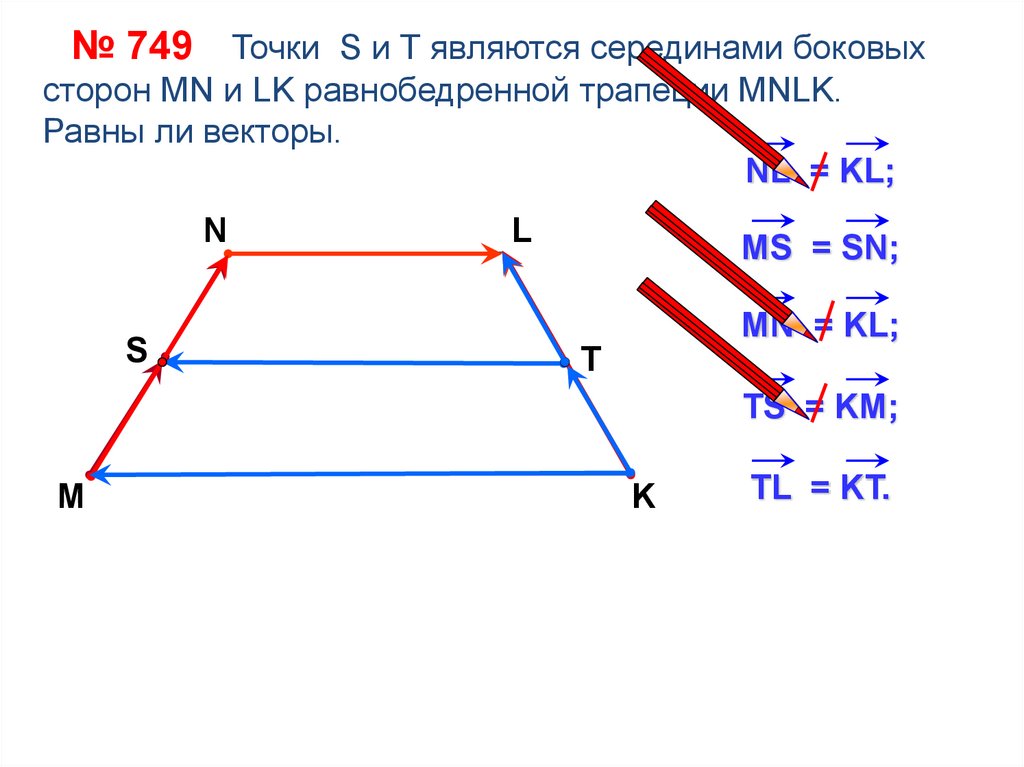
24.
№ 749 Точки S и Т являются серединами боковыхсторон MN и LK равнобедренной трапеции MNLK.
Равны ли векторы.
NL = KL;
N
S
L
MS = SN;
MN = KL;
T
TS = KM;
M
K
TL = KT.





 mathematics
mathematics








