joNfr1mpdjJnJfwsj7cWivdn7rTOzSlAsNruXIwj

1. ДВУГРАННЫЙ УГОЛ

2. ЦЕЛИ ОБУЧЕНИЯ:

10.3.3 знать определение угла между плоскостями
(двугранный угол), уметь изображать и находить
его величину

3.

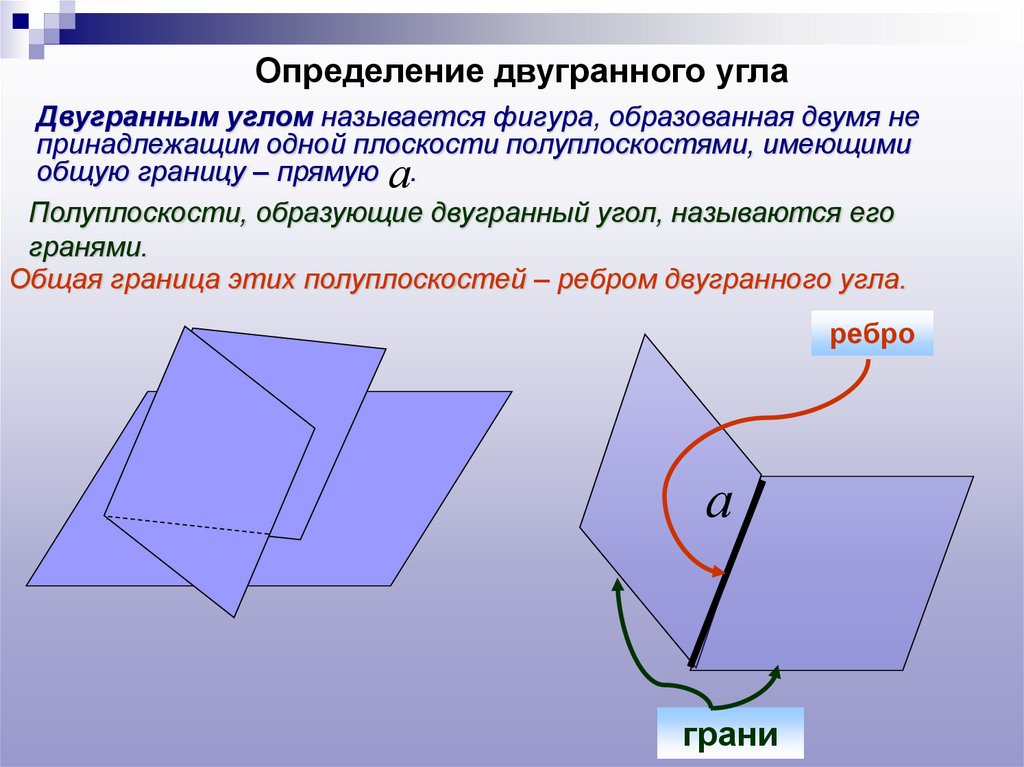
Определение двугранного угла
Двугранным углом называется фигура, образованная двумя не
принадлежащим одной плоскости полуплоскостями, имеющими
общую границу – прямую а.
Полуплоскости, образующие двугранный угол, называются его
гранями.
Общая граница этих полуплоскостей – ребром двугранного угла.
ребро
а
грани

4.

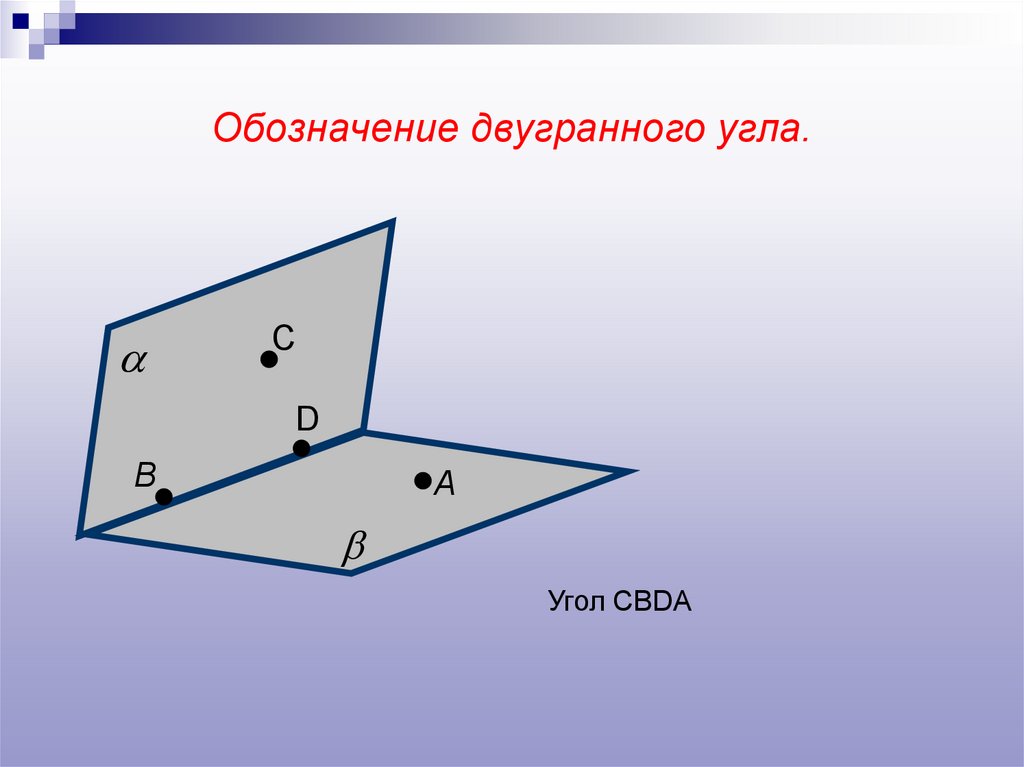
5. Обозначение двугранного угла.

С
D
В
А
Угол CBDA

6.

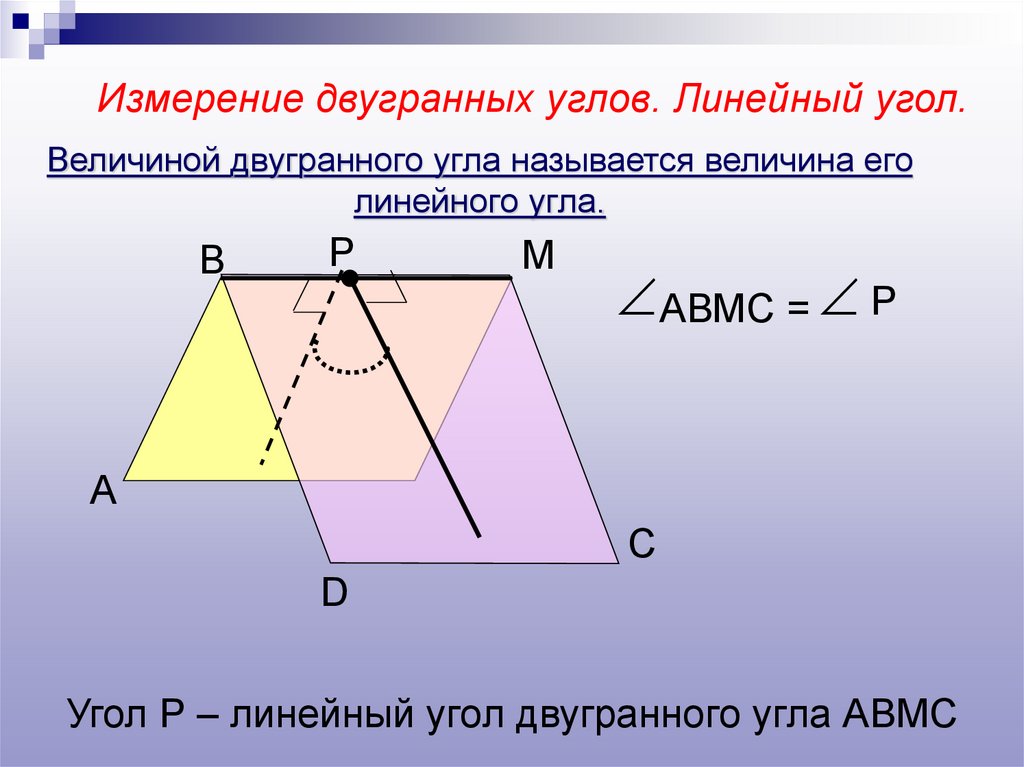
Измерение двугранных углов. Линейный угол.
Величиной двугранного угла называется величина его
линейного угла.
В
Р
М
АВМС = Р
А
С
D
Угол Р – линейный угол двугранного угла АВМС

7.

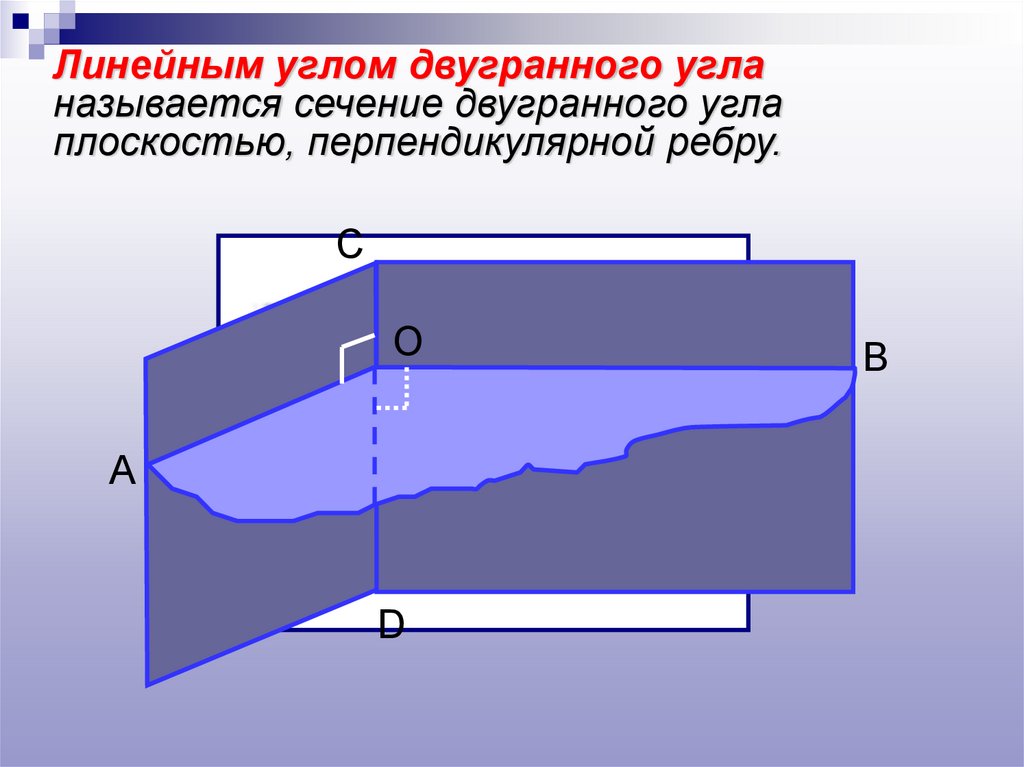
Линейным углом двугранного угла
называется сечение двугранного угла
плоскостью, перпендикулярной ребру.
С
О
А
D
В

8.

Способ нахождения (построения) линейного угла.
1. Найти ( увидеть) ребро и грани двугранного
угла
2. В гранях найти направления ( прямые)
перпендикулярные ребру
3. (при необходимости) заменить выбранные
направления параллельными им лучами с общим
началом на ребре двугранного угла
При изображении сохраняется параллельность и
отношение длин параллельных отрезков

9.

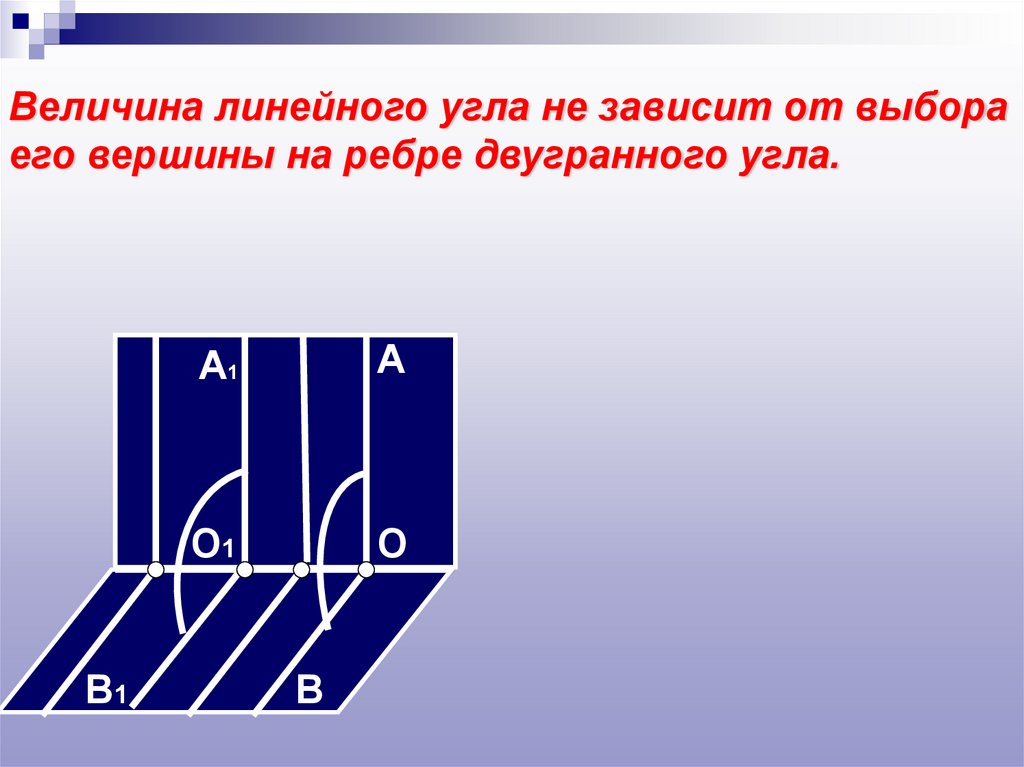
Величина линейного угла не зависит от выбора
его вершины на ребре двугранного угла.
B1
A1
A
O1
O
B

10.

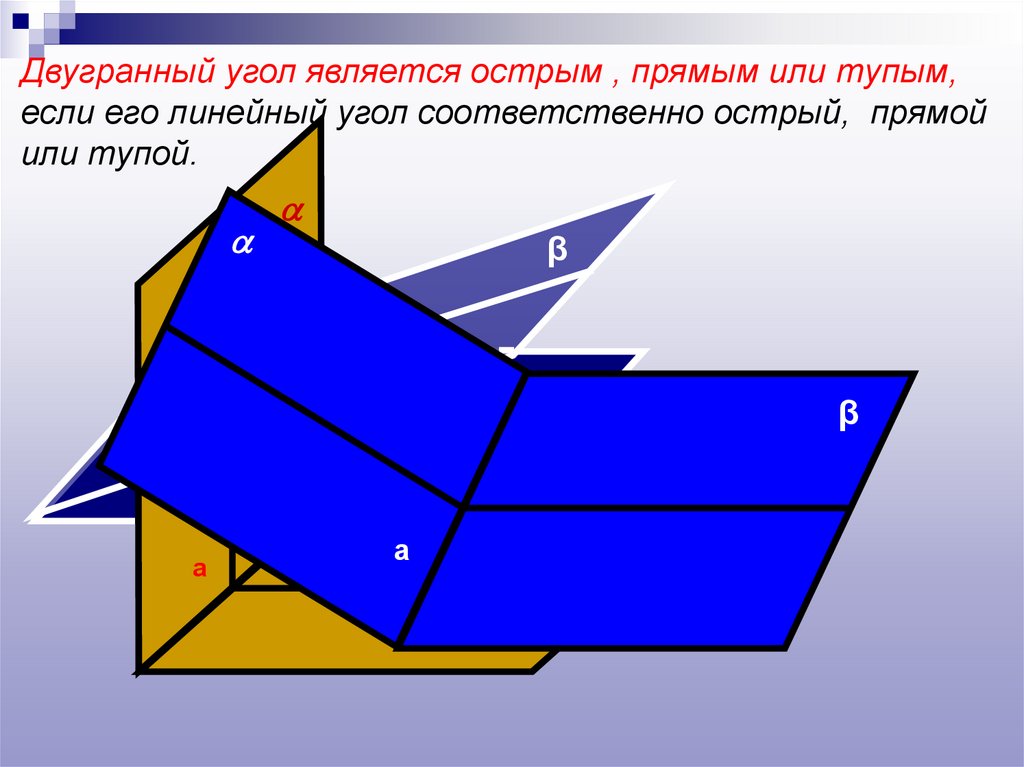
Двугранный угол является острым , прямым или тупым,
если его линейный угол соответственно острый, прямой
или тупой.
β
β
а
а
β

11.

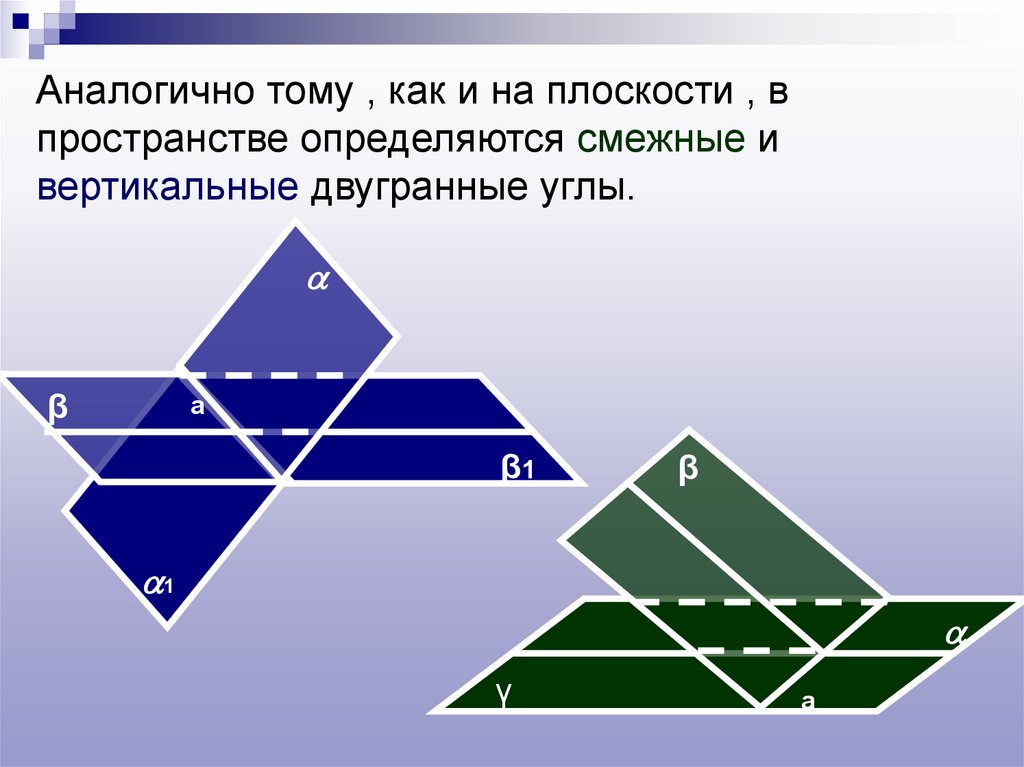
Аналогично тому , как и на плоскости , в
пространстве определяются смежные и
вертикальные двугранные углы.
β
а
β1
β
1
γ
а

12.

Углом между двумя пересекающимися
плоскостями называется наименьший из
двугранных углов, образованных при их
пересечении.
Угол между параллельными или совпадающими
плоскостями полагается равным нулю.

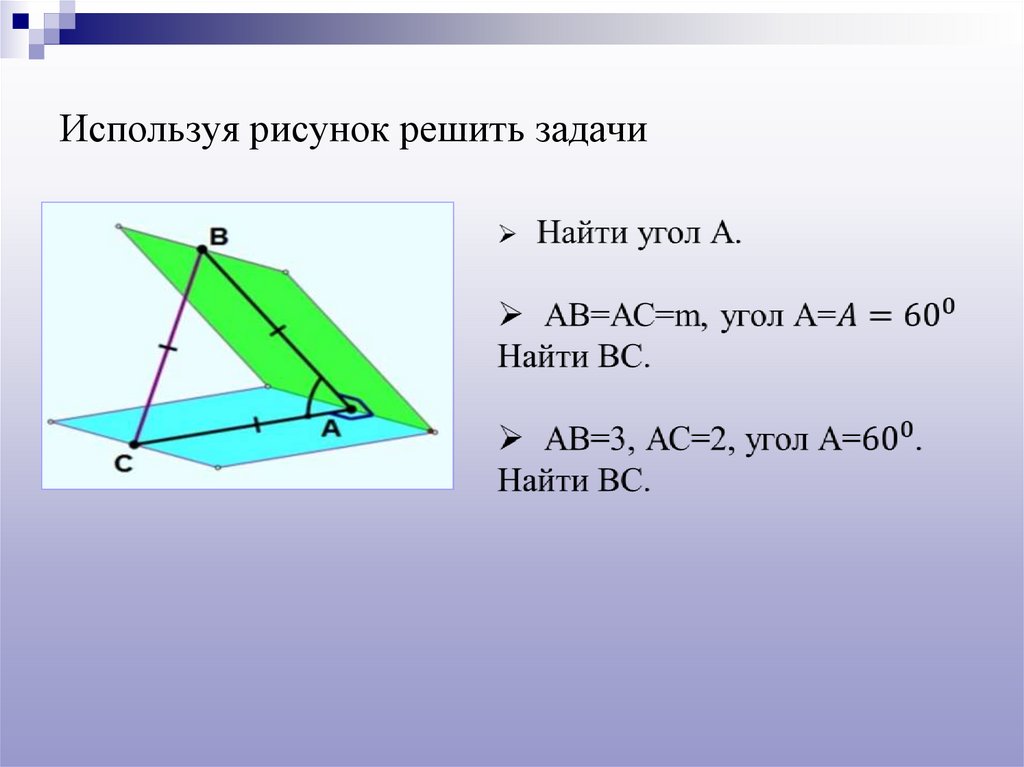
13. Используя рисунок решить задачи

14.

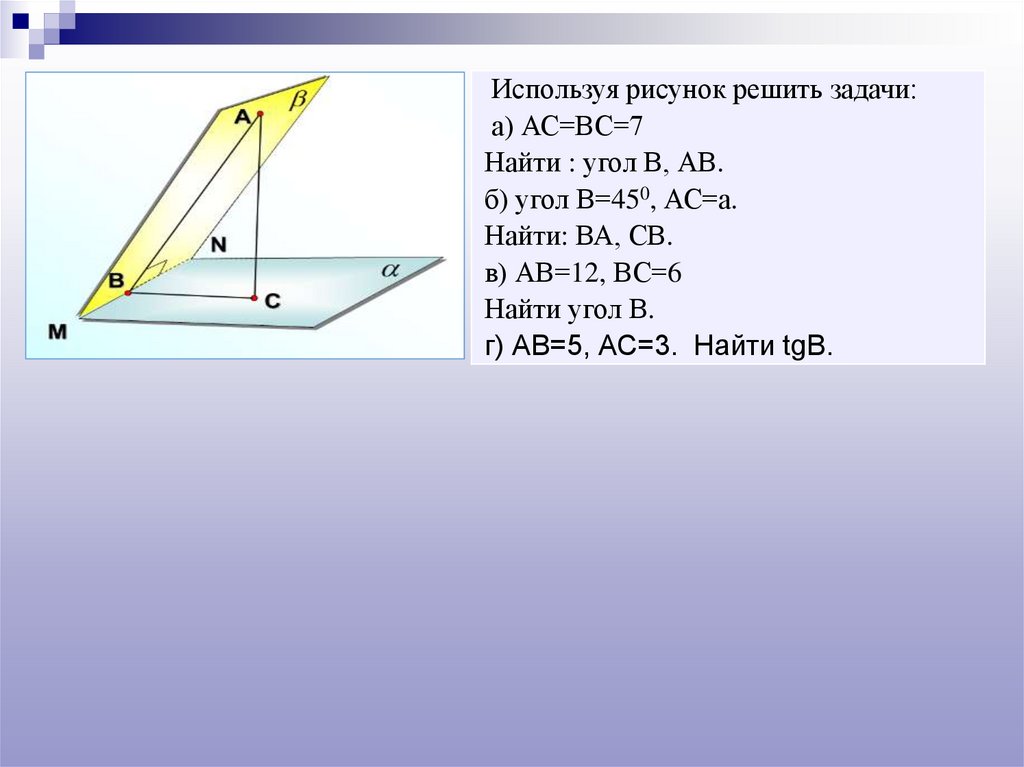
Используя рисунок решить задачи:
а) АС=ВС=7
Найти : угол В, АВ.
б) угол В=450, АС=а.
Найти: ВА, СВ.
в) АВ=12, ВС=6
Найти угол В.
г) АВ=5, АС=3. Найти tgB.