3. Содержание обучения мат-ке уч-хся с ТНР

1.

Содержание обучения
математике учащихся с
тяжелыми нарушениями речи
Лектор: Фатихова Лидия Фаварисовна, к.п.н., доцент
кафедры специальной педагогики и психологии БГПУ
им. М. Акмуллы

2.

План лекции:
1. Цели и задачи обучения математике детей с
тяжелыми нарушениями речи.
2. Образовательная программа по математике для
детей с тяжелыми нарушениями речи.
3. Методы и приемы обучения математике детей с
тяжелыми нарушениями речи.

3.

1.
Основные цели и
математике
детей
нарушениями речи.
задачи обучения
с
тяжелыми
Уровень
Описание целей (задач)
1. Общеобразовательная
цель
формирование системы доступных математических
знаний, умений и навыков, необходимых в повседневной
жизни и в будущей профессии
2. Основные задачи
1) сформировать у обучающихся стойкие
вычислительные навыки;
2) сформировать умение анализировать условие задачи,
определять связи между ее отдельными
компонентами, находить правильное решение задачи;
3) развивать математические способности;
4) способствовать развитию внимания, памяти,
восприятия, мышления, логических операций
сравнения, классификации, сериации, умозаключения.
3. Специальные задачи
1) формирование навыков фонетически правильной
разговорной речи;
2) расширение лексического запаса;
3) обучение грамматически правильному оформлению
высказывания, чтению и письму.

4.

1)
2)
3)
4)
5)
6)
7)
Формируемые умения и навыки в процессе обучения
математике
представления о натуральном числе, нуле, натуральном ряде
чисел, об обыкновенных и десятичных дробях;
представления об основных величинах (длине отрезка,
стоимости, массе предметов, площади фигуры, объеме и
емкости тел, времени), единицах измерения величин и их
соотношениях;
знание метрической системы мер, мер времени и умение
практически пользоваться ими;
умение производить основные арифметические действия с
многозначными числами и дробями;
умение вычислять значение числового выражения (со скобками
и без них), находить числовое значение простейшего буквенного
выражения при заданных числовых значениях входящих в него
букв;
умение решать простые и составные задачи в 3-4 действия;
представление о плоских и объемных геометрических фигурах,
знание их свойств, построение этих фигур с помощью
чертежных инструментов (линейки, циркуля, чертежного
треугольника, транспортира).

5.

1)
2)
3)
4)
Этапы формирования счетных операций
(по П. Я. Гальперину)
выполнение математического действия на основе
предметных действий с конкретными предметами (этап
материализации действия) сначала с помощью учителя,
затем самостоятельно;
выполнение математического действия с опорой на
наглядность и громкую речь, но без использования
практических действий с конкретными предметами;
выполнение математических действий только в речевом
плане;
выполнение математических действий в умственном плане,
во внутренней речи.

6.

2. Учебная программа по математике для
детей с тяжелыми нарушениями речи.
Отделение
Группы детей
I отделение
дети с алалией, афазией, ринолалией, дизартрией и
заиканием, имеющие общее недоразвитие речи и нарушения
чтения и письма, препятствующие обучению в
общеобразовательных организациях.
II отделение
дети с тяжелой степенью выраженности заикания при
нормальном развитии компонентов речевой функциональной
системы.
• Сроки получения начального образования обучающимися с ТНР
пролонгируются с учетом психофизиологических возможностей и
индивидуальных особенностей развития детей данной категории,
которые определяются Стандартом (ФГОС НО для обучающихся с ОВЗ - 5.1., 5.2.).
• Нормативный срок освоения адаптированной основной образовательной
программы начального общего образования для обучающихся с ТНР
(вариант В) составляет 5 лет в I отделении (подготовительный – IV
классы) и 4 года во II отделении (I-IV классы).

7.

Примерная основная образовательная программа,
рассчитанная на 4 года (5 лет), предполагает, что обучающиеся
на ступени начального образования овладеют основами
логического и алгоритмического мышления, пространственного
воображения и математической речи, приобретут необходимые
вычислительные умения. Программа по математике включает
следующие разделы:
1. Числа и величины;
2. Арифметические действия;
3. Работа с текстовыми задачами;
4. Пространственные отношения. Геометрические фигуры;
5. Геометрические величины;
6. Работа с информацией.
На изучение математики отводится: в подготовительном и I
классах – по 4 ч, по II, III, IV классах – по 6 ч, в V классе – по 7 ч
в неделю.

8.

1)
2)
3)
4)
5)
6)
Положения, реализуемые в построении программы
обучения математике и учебников по математике
излагать арифметический материал по концентрам;
рассматривать вопросы алгебраической и геометрической
пропедевтики не отдельно, а попутно и по возможности во
взаимосвязи с арифметическим материалом;
раскрывать вопросы теории в органической связи с
соответствующими практическими вопросами;
включать новый материал небольшими частями и
систематически повторять ранее изученное, раскрывая его
связи с новым, показывая применение его в новых
условиях;
рассматривать каждое понятие в развитии, постепенно
раскрывая его свойства и связи с другими понятиями,
обеспечивая на каждом этапе соответствующие обобщения;
широко использовать при изучении материала метод
сравнения и др.

9.

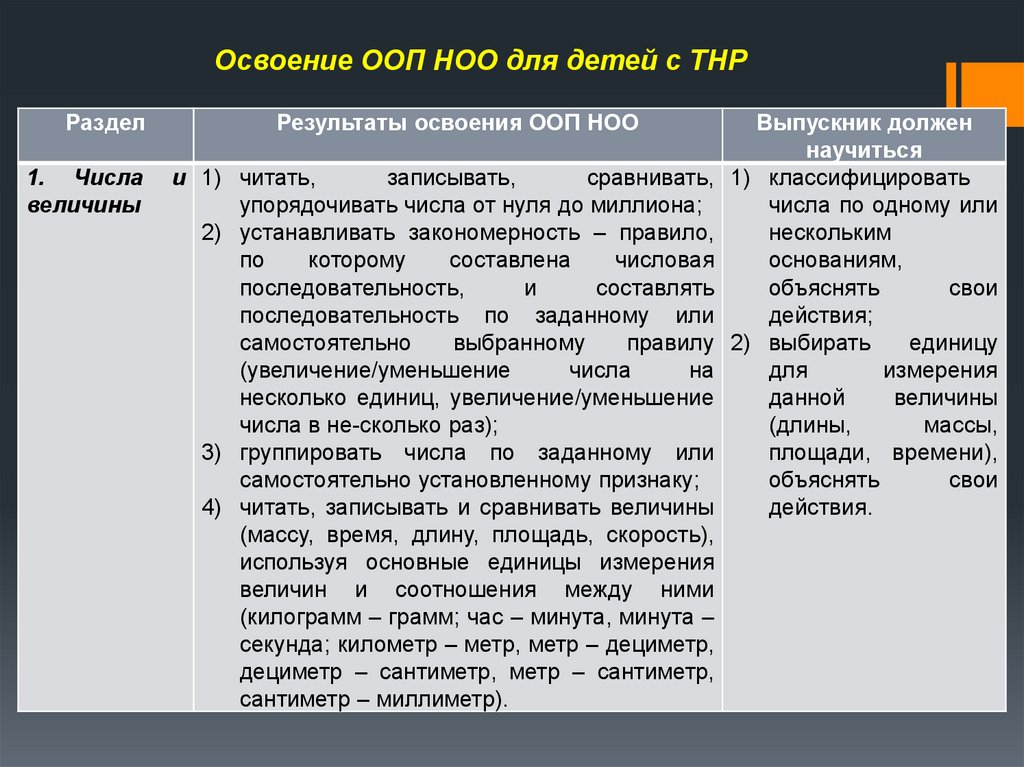
Освоение ООП НОО для детей с ТНР
Раздел
1. Числа
величины
Результаты освоения ООП НОО
и 1)
2)
3)
4)
Выпускник должен
научиться
читать,
записывать,
сравнивать, 1) классифицировать
упорядочивать числа от нуля до миллиона;
числа по одному или
устанавливать закономерность – правило,
нескольким
по
которому
составлена
числовая
основаниям,
последовательность,
и
составлять
объяснять
свои
последовательность по заданному или
действия;
самостоятельно
выбранному
правилу 2) выбирать
единицу
(увеличение/уменьшение
числа
на
для
измерения
несколько единиц, увеличение/уменьшение
данной
величины
числа в не-сколько раз);
(длины,
массы,
группировать числа по заданному или
площади, времени),
самостоятельно установленному признаку;
объяснять
свои
читать, записывать и сравнивать величины
действия.
(массу, время, длину, площадь, скорость),
используя основные единицы измерения
величин и соотношения между ними
(килограмм – грамм; час – минута, минута –
секунда; километр – метр, метр – дециметр,
дециметр – сантиметр, метр – сантиметр,
сантиметр – миллиметр).

10.

Раздел
2.
Арифметические
действия
Результаты освоения ООП НОО
1)
2)
3)
4)
Выпускник должен
научиться
выполнять письменно действия с
1) выполнять действия
многозначными числами (сложение,
с величинами;
вычитание, умножение и деление на
2) использовать
однозначное, двузначное числа в
свойства
пределах 10 000) с использованием
арифметических
таблиц сложения и умножения чисел,
действий для
алгоритмов письменных
удобства
арифметических действий (в том
вычислений;
числе деления с остатком);
3) проводить проверку
выполнять устно сложение,
правильности
вычитание, умножение и деление
вычислений (с
однозначных, двузначных и
помощью обратного
трёхзначных чисел в случаях,
действия, прикидки и
сводимых к действиям в пределах 100
оценки результата
(в том числе с нулём и числом 1);
действия и др.).
выделять неизвестный компонент
арифметического действия и находить
его значение;
вычислять значение числового
выражения (содержащего 2-3
арифметических действия, со
скобками и без скобок).

11.

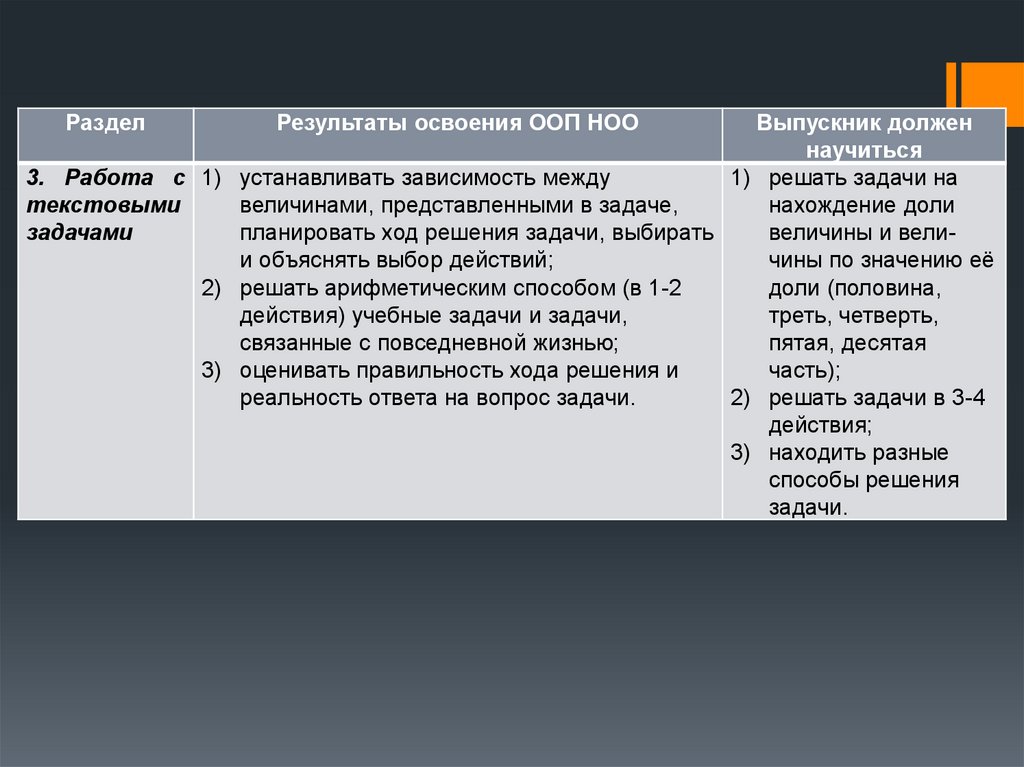
Раздел
Результаты освоения ООП НОО
Выпускник должен
научиться
3. Работа с 1) устанавливать зависимость между
1) решать задачи на
текстовыми
величинами, представленными в задаче,
нахождение доли
задачами
планировать ход решения задачи, выбирать
величины и велии объяснять выбор действий;
чины по значению её
2) решать арифметическим способом (в 1-2
доли (половина,
действия) учебные задачи и задачи,
треть, четверть,
связанные с повседневной жизнью;
пятая, десятая
3) оценивать правильность хода решения и
часть);
реальность ответа на вопрос задачи.
2) решать задачи в 3-4
действия;
3) находить разные
способы решения
задачи.

12.

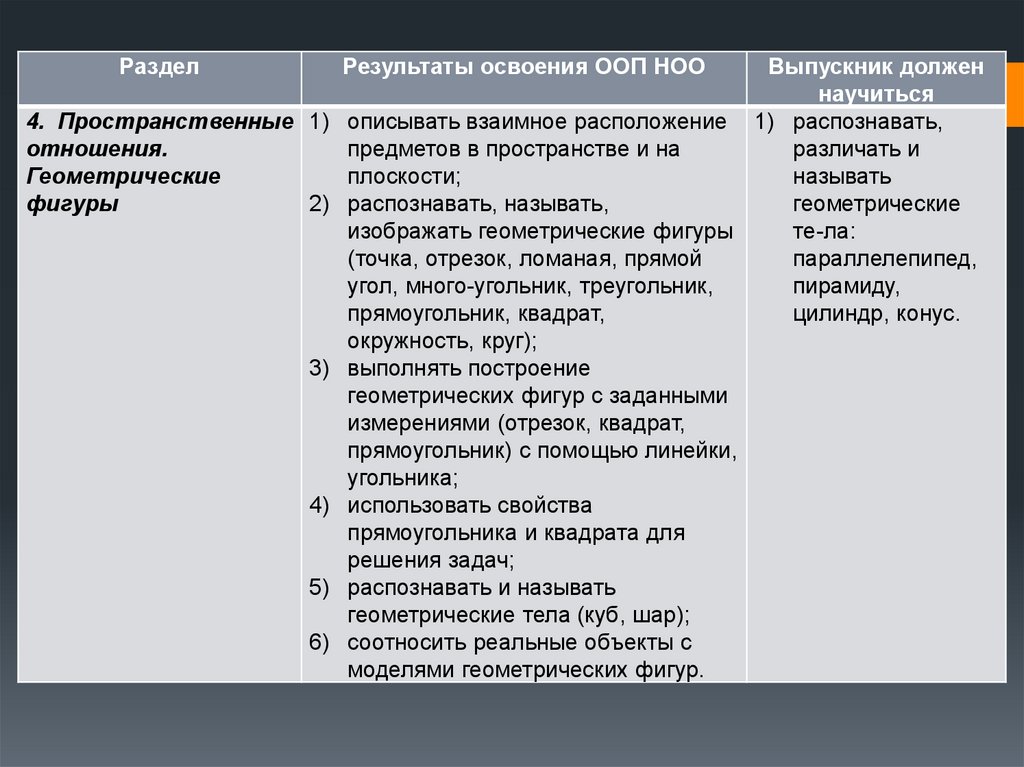
Раздел
Результаты освоения ООП НОО
4. Пространственные 1)
отношения.
Геометрические
фигуры
2)
3)
4)
5)
6)
Выпускник должен
научиться
описывать взаимное расположение 1) распознавать,
предметов в пространстве и на
различать и
плоскости;
называть
распознавать, называть,
геометрические
изображать геометрические фигуры
те-ла:
(точка, отрезок, ломаная, прямой
параллелепипед,
угол, много-угольник, треугольник,
пирамиду,
прямоугольник, квадрат,
цилиндр, конус.
окружность, круг);
выполнять построение
геометрических фигур с заданными
измерениями (отрезок, квадрат,
прямоугольник) с помощью линейки,
угольника;
использовать свойства
прямоугольника и квадрата для
решения задач;
распознавать и называть
геометрические тела (куб, шар);
соотносить реальные объекты с
моделями геометрических фигур.

13.

Раздел
Результаты освоения ООП НОО
5. Геометрические 1) измерять длину отрезка;
величины
2) вычислять периметр треугольника,
прямоугольника и квадрата,
площадь прямоугольника и
квадрата;
3) оценивать размеры геометрических
объектов, расстояния приближённо
(на глаз).
Выпускник должен
научиться
1) вычислять периметр
многоугольника,
площадь фигуры,
составленной из
прямоугольников.

14.

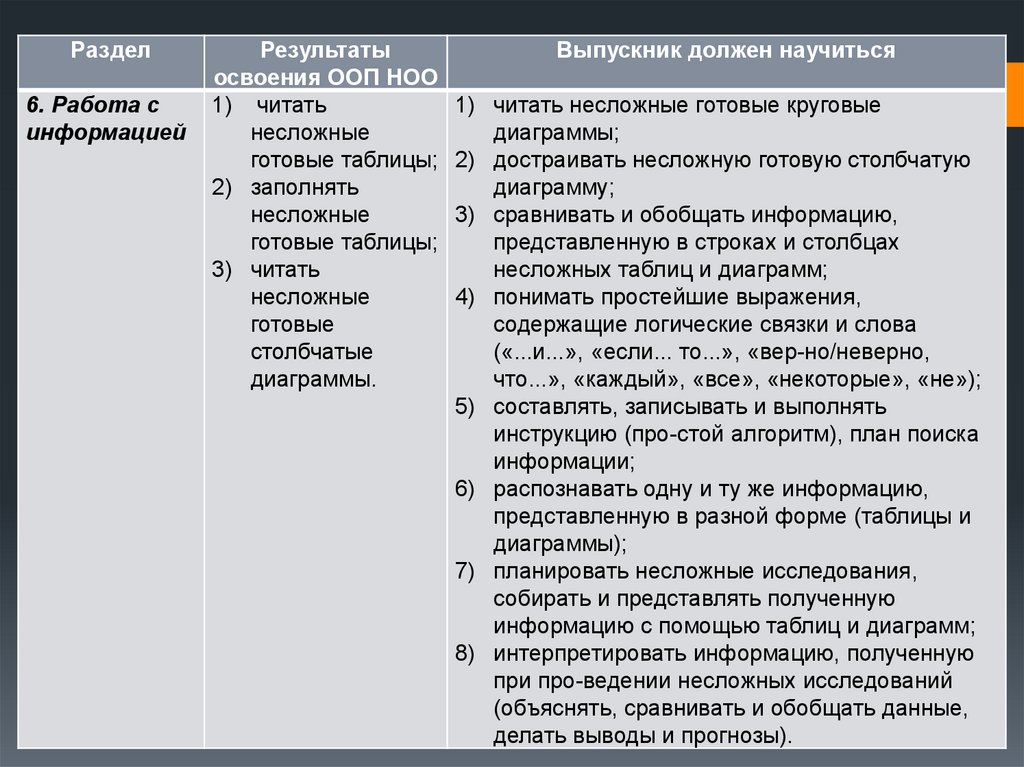
Раздел
6. Работа с
информацией
Результаты
освоения ООП НОО
1) читать
несложные
готовые таблицы;
2) заполнять
несложные
готовые таблицы;
3) читать
несложные
готовые
столбчатые
диаграммы.
Выпускник должен научиться
1) читать несложные готовые круговые
диаграммы;
2) достраивать несложную готовую столбчатую
диаграмму;
3) сравнивать и обобщать информацию,
представленную в строках и столбцах
несложных таблиц и диаграмм;
4) понимать простейшие выражения,
содержащие логические связки и слова
(«...и...», «если... то...», «вер-но/неверно,
что...», «каждый», «все», «некоторые», «не»);
5) составлять, записывать и выполнять
инструкцию (про-стой алгоритм), план поиска
информации;
6) распознавать одну и ту же информацию,
представленную в разной форме (таблицы и
диаграммы);
7) планировать несложные исследования,
собирать и представлять полученную
информацию с помощью таблиц и диаграмм;
8) интерпретировать информацию, полученную
при про-ведении несложных исследований
(объяснять, сравнивать и обобщать данные,
делать выводы и прогнозы).

15.

Используемые учебники и пособия
Используются традиционные учебники, авторами которых являются
М. А. Бантова, Г. В. Бельтюкова, С. И. Волкова, Н. Б. Истомина,
М. И. Моро и др. Авторы-составители предлагают пользоваться
учебными комплектами, которые традиционно включают
непосредственно сами учебники для 1–4 классов, а также рабочие
тетради для индивидуальной работы учащихся.
Типовые учебники по математике основываются на том, что курс
математики в начальной школе интегрированный, и содержит
арифметический, алгебраический и геометрический материал. В
объяснительной записке к курсу математики в начальных классах
рекомендуется формировать математические умения и навыки по
следующим направлениям: понятие числа – счётные операции –
решение задачи. Умение пользоваться операциями счёта, с одной
стороны, и умозаключениями с другой, способствует развитию
умения решать математические задачи.

16.

Приёмы учебной деятельности младших школьников,
формируемые в процессе обучения математики
Группа приемов
Приемы
1. Общеучебные
приёмы, не
зависящие от
специфики
предмета
математики
(используются в
разных учебных
предметах)
1) приёмы общей, внешней организации учебной деятельности –
организация внимания, планирование, работа с учебником,
самоконтроль, организация домашней работы и т. д.; их можно
также назвать приёмами управления учебной деятельностью;
2) приёмы мыслительной (внутренней) деятельности – овладение
и оперирование представлениями, понятиями, суждениями,
умозаключениями, мыслительными операциями.
2. Общие приёмы
1) приёмы работы с учебником математики и математическими
учебной
таблицами, приёмы организации домашней работы по
деятельности по
математике, ведение тетради по математике и т. д. Они
математике
незначительно отличаются от соответствующих общеучебных
(общематематическ
приёмов;
ие приёмы)
2) приёмы мыслительной деятельности в сфере математических
используются во
объектов: приёмы работы с математическими понятиями,
всех
суждениями (аксиомами и теоремами разных видов),
математических
умозаключениями (индуктивными и дедуктивными
дисциплинах
доказательствами теорем), приёмы характерных для
математики мыслительных операций (анализ,
абстрагирование, конкретизация и т. п.).

17.

Группа приемов
Приемы
3. Специальные приёмы
учебной деятельности по
отдельным математическим
дисциплинам (арифметике,
геометрии)
общематематические приёмы, которые принимают
свою особую форму в соответствии со спецификой
содержания курса и его специфических задач.
4. Частные приёмы учебной
деятельности
специальные приёмы, которые конкретизированы для
решения более узких задач.

18.

3 группы результатов обучения математике в начальной
школе
Группа
Умения
1. Личностные
1) готовность ученика целенаправленно использовать знания в
учении и в повседневной жизни для исследования
математической сущности предмета (явления, события, факта);
2) познавательный интерес к математической науке.
2. Метапредметные
1) способность анализировать учебную ситуацию с точки зрения
математических характеристик, устанавливать количественные
и пространственные отношения объектов окружающего мира,
строить алгоритм поиска необходимой информации,
определять логику решения практической и учебной задачи;
2) умение моделировать – решать учебные задачи с помощью
знаков (символов), планировать, контролировать и
корректировать ход решения учебной задачи.
3. Предметные
1) освоенные знания о числах и величинах, арифметических
действиях, текстовых задачах, геометрических фигурах;
2) умения выбирать и использовать в ходе решения изученные
алгоритмы, свойства арифметических действий, способы
нахождения величин, приемы решения задач,
3) умения использовать знаково-символические средства, в том
числе модели и схемы, таблицы, диаграммы для решения
математических задач.

19.

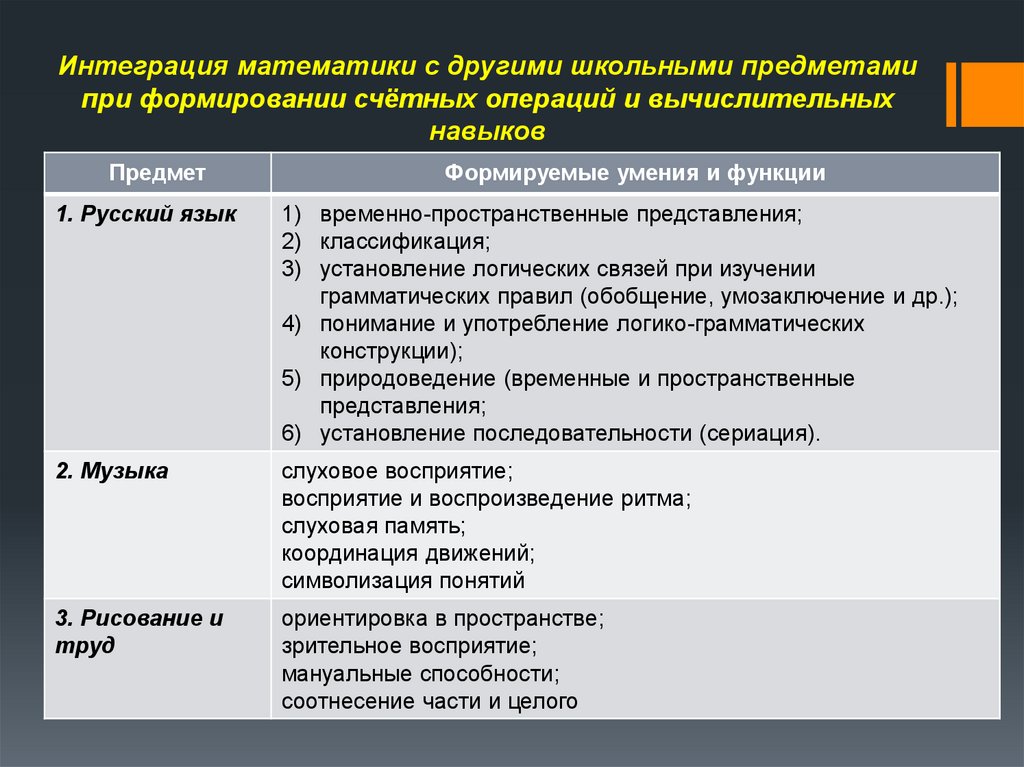
Интеграция математики с другими школьными предметами
при формировании счётных операций и вычислительных
навыков
Предмет
Формируемые умения и функции
1. Русский язык
1) временно-пространственные представления;
2) классификация;
3) установление логических связей при изучении
грамматических правил (обобщение, умозаключение и др.);
4) понимание и употребление логико-грамматических
конструкции);
5) природоведение (временные и пространственные
представления;
6) установление последовательности (сериация).
2. Музыка
слуховое восприятие;
восприятие и воспроизведение ритма;
слуховая память;
координация движений;
символизация понятий
3. Рисование и
труд
ориентировка в пространстве;
зрительное восприятие;
мануальные способности;
соотнесение части и целого

20.

3. Методы и приемы обучения математике
детей с тяжелыми нарушениями речи.
Метод (прием)
1. Объяснение
Характеристика
Применяется для овладения теоретическим учебным
материалом. Неотъемлемой частью данного метода является
постановка вопросов, помогающих понять затруднения учащихся
и устранить их.
Особенностью этого метода являются теоретические
доказательства, то есть:
постановка познавательной задачи, адекватной уровню знаний и
развития учащихся;
строгий подбор фактического материала;
определенная форма рассуждений (аналитическое и
синтетическое объяснение, наблюдения и выводы, индукция или
дедукция);
использование иллюстративного материала (схем, рисунков,
картин);
формулировка выводов;
дополнительные разъяснения, если они необходимы в связи с
конкретной ситуацией обучения.

21.

Метод (прием)
Характеристика
2. Демонстрация
Позволяет развивать элементарные представления учащихся, учит
детей наблюдать предмет, явление, выделять в них основные
черты, сравнивать и пр.
Требования:
1) демонстрируемый объект должен быть хорошо виден всем
учащимся;
2) нельзя допускать предварительный осмотр демонстрируемого
учащимися. В связи с их особенностями восприятия и
внимания необходимое пособие нужно показывать только в
момент объяснения;
3) каждый учащийся должен действовать в соответствии с
поставленной задачей и обращать внимание на те части
демонстрируемого объекта, которые связаны с изучаемой на
уроке темой;
4) учащимся необходимо давать задание описать объект
словесно, это способствует развитию наблюдательности и
формированию правильной, логичной речи;
5) дети должны формулировать итоги наблюдений на
максимально доступном для них уровне.
6) Демонстрировать объект можно перед или после объяснения
учебного материала.

22.

Метод (прием)
Характеристика
3. Беседа
Представляет собой вопросно-ответную форму овладения
материалом. Главным требованием является система
продуманных вопросов и предполагаемых ответов учащихся.
Вопросы должны быть взаимосвязаны, подчинены идее урока,
поставлены на доступном учащимся уровне. Для более слабых
учеников следует задавать конкретные вопросы, требующие
односложного, краткого ответа или ответа в форме картинки,
рисунка и пр. Вопрос, заданный более сильному учащемуся,
предполагает развернутый ответ. Вопросы могут быть заданы
как в устной, так и в письменной форме. Последняя форма
беседы позволяет работать не только над устной, но и над
письменной речью учащихся.
4. Сравнение
Направлен на формирование способов нахождения сходства и
различия, выделения существенных признаков и отвлечения от
несущественных, использовании приемов классификации и
дифференциации, установлении причинно-следственных связей
между понятиями.
5. Материализация
Направлен на овладение умением конкретизировать любое
отвлеченное понятие, использовать его в жизненных ситуациях.
6. Повторение речи Направлен на формирование устной речи учащихся, вводится
учителя
хоровое, а затем индивидуальное комментирование предметнопрактической деятельности и действий с числами.

23.

Метод (прием)
Характеристика
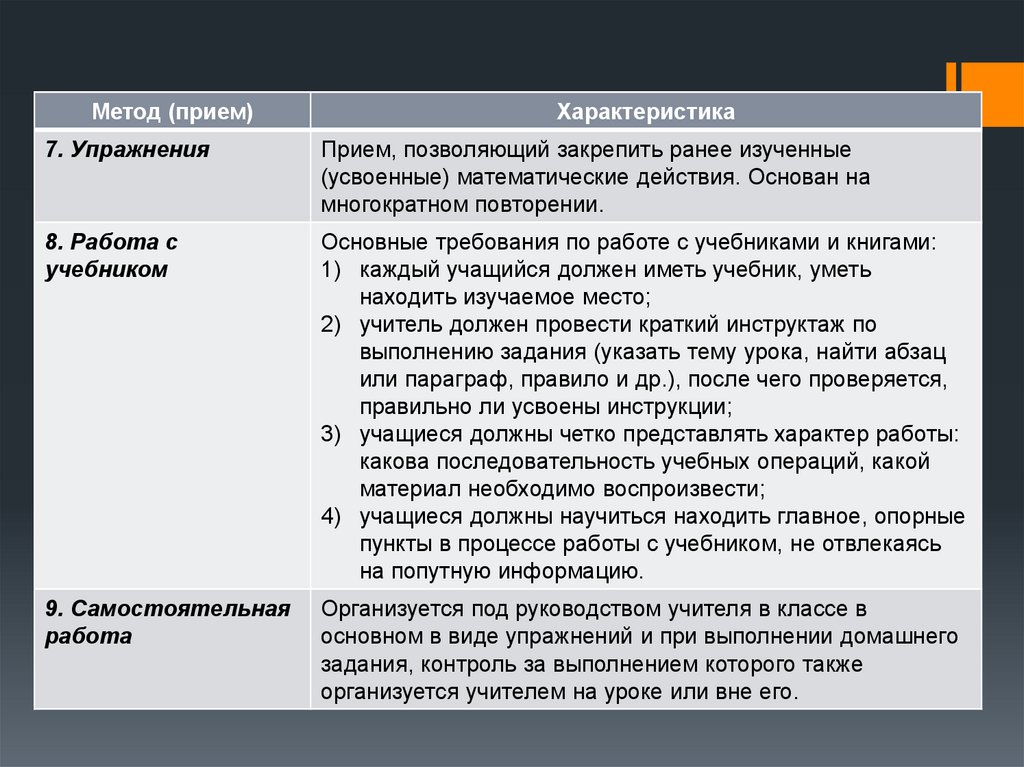
7. Упражнения
Прием, позволяющий закрепить ранее изученные
(усвоенные) математические действия. Основан на
многократном повторении.
8. Работа с
учебником
Основные требования по работе с учебниками и книгами:
1) каждый учащийся должен иметь учебник, уметь
находить изучаемое место;
2) учитель должен провести краткий инструктаж по
выполнению задания (указать тему урока, найти абзац
или параграф, правило и др.), после чего проверяется,
правильно ли усвоены инструкции;
3) учащиеся должны четко представлять характер работы:
какова последовательность учебных операций, какой
материал необходимо воспроизвести;
4) учащиеся должны научиться находить главное, опорные
пункты в процессе работы с учебником, не отвлекаясь
на попутную информацию.
9. Самостоятельная
работа
Организуется под руководством учителя в классе в
основном в виде упражнений и при выполнении домашнего
задания, контроль за выполнением которого также
организуется учителем на уроке или вне его.

24.

Спасибо за внимание!