Similar presentations:
УМК ПНШ. Инновационные подходы к программам начального общего образования
1.
900igr.net2. Инновационные подходы к программам начального общего образования
В целевой установке начального обучения – от усвоения знаний,умений, навыков к формированию универсальных учебных действий,
обеспечивающих умение школьников учиться;
В изложении учебного материала в учебниках – от изолированного
изучения учащимися системы научных понятий, составляющих
содержание учебного предмета, к включению содержания в общий
контекст системы межпредметных связей;
В технологии – от урочной системы обучения к интегрированной
системе урочной и внеурочной деятельности, которая стала
неотъемлемой частью образовательного процесса в школе;
В новом содержании программных требований к результатам обучения
– наряду с требованиями к усвоению предметных ЗУНов заложены
требования к формированию УУД, необходимых учащимся при
решении учебных творческих задач, в практической деятельности и
повседневной жизни;
В дифференциации содержания – в балансе основного и
ознакомительного материалов, способствующем расширению
кругозора младших школьников.
3. УМК «Перспективная начальная школа»
• Результат многолетней работысотрудников РАН, МГПУ, АПК и ППРО,
а так же сотрудников РАО.
• Программа прошла экспертизу в 2002
году в Министерстве образования РФ.,
полностью соответствует стандартам
второго поколения.
4. Цели изучения математики в начальной школе (стандарты второго поколения и УМК «ПНШ»)
Изучение математики в начальнойшколе направлено на достижение
следующих целей:
• Математическое развитие младших
школьников: использование
математических представлений для
описания окружающих предметов,
процессов, явлений; формирование
способности к продолжительной
умственной деятельности, основ
логического мышления,
пространственного воображения,
математической речи и аргументации.
Курс математики в УМК «ПНШ» имеет
цель не только ввести в ребенка в
абстрактный мир математических
понятий и их свойств, охватывающих
весь материал обязательного
минимума начального
математического образования, но и
дать первоначальные навыки
ориентации в той реальной
действительности, которая
описывается (моделируется) с
помощью этих понятий, а именно:
окружающий мир как множество форм,
множество предметов, отличающихся
величиной, которую можно выразить
числом, как разнообразие классов
конечных равночисленных множеств и
т.п., а так же предложить ребенку
соответствующие способы познания
окружающей действительности.
5. Цели изучения математики в стандартах второго поколения и в УМК «ПНШ»
Изучение математики в начальной школенаправлено на достижение следующих
целей:
Освоение начальных математических
знаний. Формирование умения решать
учебные и практические задачи
средствами математики: вести поиск
информации (фактов, сходств,
различий, закономерностей,
оснований для упорядочивания,
вариантов); понимать значение
величин и способов их измерения;
использовать арифметические
способы для разрешения сюжетных
ситуаций; работать с алгоритмами
выполнения арифметических
действий, решения задач, проведения
простейших построений. Проявлять
математическую готовность к
продолжению образования.
Воспитание критичности мышления,
интереса к умственному труду,
стремления использовать
математические знаниями в
повседневной жизни.
Имеется полное согласование целей
данного курса и целей,
предусмотренных обязательным
минимумом начального общего
образования, которое заключается в
овладении знаниями и умениями,
необходимыми для успешного
решения учебных и практических
задач и продолжения образования;
развитие личности ребенка, его
мышления как основы развития
других психических процессов:
памяти, внимания, воображения,
математической речи и способов
деятельности; формирование основ
общих учебных умений и способов
деятельности, связанных с методами
познания окружающего мира
(наблюдение, измерение,
моделирование), приемов
мыслительной деятельности (анализ,
синтез, сравнение, классификация,
обобщение), способов организации
учебной деятельности (планирование,
самоконтроль, самооценка).
6. Основное содержание (стандарты и УМК «ПНШ»)
• «Числа и величины»,«Арифметические
действия», «Текстовые
задачи»,
«Пространственные
отношения.
Геометрические
фигуры»,
«Геометрические
величины», «Работа с
данными»
• Содержание курса
УМК «ПНШ»взаимосвязанное
развитие пяти основных
содержательных линий:
арифметической,
геометрической,
величинной,
алгоритмической
(обучение решению
задач), и
алгебраической.
7. Стандарты второго поколения
• В результате освоения предметного содержания курса уучащихся формируются общие учебные умения и способы
познавательной деятельности; осуществляется знакомство с
математическим языком, формируются речевые умения;
развиваются организационные умения: планирование этапов
предстоящей работы, определение последовательности
учебных действий; осуществление контроля и оценка их
правильности, поиск путей преодоления ошибок. В процессе
обучения математике школьник учится участвовать в
совместной деятельности при решении математических задач
(распределять поручения для поиска доказательств, выбора
рационального способа, поиска и анализа информации),
проявлять инициативу и самостоятельность.
• Организуя обучение, целесообразно использовать
дифференцированный подход к учащимся. Это способствует
нормализации нагрузки обучающихся, обеспечивает их
посильное отношение к учебе. (работа в парах и тетради для
самостоятельной работы)
8. Основное содержание примерной программы
• Основное содержание примерной программыпредставлено в двух частях: собственно
содержание курса математики в начальной
школе и основные виды учебной
деятельности школьника. Преломление
видов деятельности в предметном
содержании отражено в тематическом
планировании в графе «Характеристика
деятельности учащихся»
• Раздел «Тематическое планирование»
представлен тремя вариантами: базовым
вариантом и двумя вариантами с
расширенным изучением отдельных
разделов курса.
9. «Тематическое планирование» (стандарты и УМК «ПНШ»)
1. Расширяетпредставления о
математических
отношениях и
закономерностях
окружающего
мира, расширяет
эрудицию,
воспитывает
математическую
культуру;
• Курс математики «ПНШ» имеет
цель не только ввести в ребенка в
абстрактный мир математических
понятий и их свойств, но и дать
первоначальные навыки
ориентации в той реальной
действительности, которая
описывается (моделируется) с
помощью этих понятий, а именно:
окружающий мир как множество
форм, множество предметов,
отличающихся величиной,
которую можно выразить числом.
• Особенностью данного курса
является строгое следование
математической сути понятий.
10. «Тематическое планирование» (стандарты и УМК «ПНШ»)
2. Усилениегеометрической
направленности курса
во втором варианте
планирования
способствует более
углубленному
рассмотрению
вопросов, связанных с
геометрией.
• Отличительной чертой курса
является значительное
увеличение роли изучения
геометрического материала
и изучения величин, в
которых затрагивается связь
математики с окружающим
миром. Без усиления этих
содержательных линий
невозможно достичь
указанных целей, т.к.
ребенок воспринимает
окружающий мир прежде
всего как совокупность
реальных предметов,
имеющих форму и величину.
11. «Тематическое планирование» (стандарты и УМК «ПНШ»)
Третий варианториентирован на
развитие умения
работать с
информацией. В нем
расширен раздел,
посвященный работе с
данными. Школьники
учатся самостоятельно
составлять различные
схемы, инструкции
работать с таблицей
(чтение и заполнение
таблицы), диаграммой
(чтение диаграмм)и т.д.
• В УМК «ПНШ» дети на
каждом уроке работают
с информацией, учатся
ее анализировать,
систематизировать,
отбирать нужную,
дополнять
недостающую. Такая
работа ведется при
работе над задачами
(запись данных в
таблицу, использование
диаграмм), при
изучении величин и т.д.
(учет перспективы)
12. Организация внеурочной деятельности учащихся
СтандартыВ сборник включены
«Рекомендации по организации
внеурочной деятельности
учащихся» по математике.
Внеурочная деятельность
направлена на расширение и
углубление математических
представлений учащихся
начальной школы и
предполагает три направления:
участие в кружковой работе,
факультативных занятиях и
проектную деятельность.
УМК «ПНШ»
В программе «ПНШ» имеется
программа факультативных занятий
по математике.
Основная цель внеурочной
деятельности на факультативных
занятиях – изучение окружающего
мира математическими средствами.
Практические задачи являются
средством и условием
формирования способности детей
применять полученные знания на
уроках по математике ЗНАНИЯ в
ситуациях, отличных от тех, в
которых происходило их
становление.
Программа факультативных занятия по
математике служит продолжением
уроков по математике и
окружающему миру и
предусматривает участие всех
учащихся.
13.
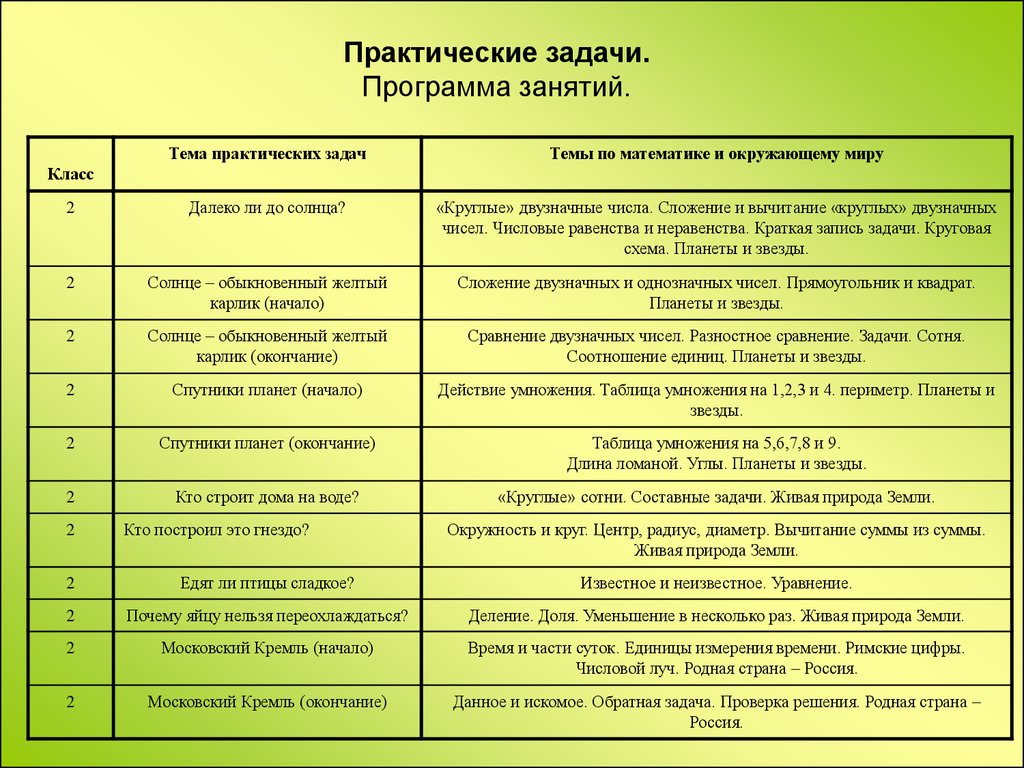
Практические задачи.Программа занятий.
Тема практических задач
Темы по математике и окружающему миру
2
Далеко ли до солнца?
«Круглые» двузначные числа. Сложение и вычитание «круглых» двузначных
чисел. Числовые равенства и неравенства. Краткая запись задачи. Круговая
схема. Планеты и звезды.
2
Солнце – обыкновенный желтый
карлик (начало)
Сложение двузначных и однозначных чисел. Прямоугольник и квадрат.
Планеты и звезды.
2
Солнце – обыкновенный желтый
карлик (окончание)
Сравнение двузначных чисел. Разностное сравнение. Задачи. Сотня.
Соотношение единиц. Планеты и звезды.
2
Спутники планет (начало)
Действие умножения. Таблица умножения на 1,2,3 и 4. периметр. Планеты и
звезды.
2
Спутники планет (окончание)
Таблица умножения на 5,6,7,8 и 9.
Длина ломаной. Углы. Планеты и звезды.
2
Кто строит дома на воде?
«Круглые» сотни. Составные задачи. Живая природа Земли.
Класс
2
Кто построил это гнездо?
Окружность и круг. Центр, радиус, диаметр. Вычитание суммы из суммы.
Живая природа Земли.
2
Едят ли птицы сладкое?
Известное и неизвестное. Уравнение.
2
Почему яйцу нельзя переохлаждаться?
Деление. Доля. Уменьшение в несколько раз. Живая природа Земли.
2
Московский Кремль (начало)
Время и части суток. Единицы измерения времени. Римские цифры.
Числовой луч. Родная страна – Россия.
2
Московский Кремль (окончание)
Данное и искомое. Обратная задача. Проверка решения. Родная страна –
Россия.
14. УМК «Перспективная начальная школа»
• Основная дидактическая идея курса – черезрассмотрение частного к пониманию общего
для решения частного. Знакомство с тем или
иным математическим понятием
осуществляется при рассмотрении
конкретной реальной ситуации,
соответствующий анализ которой позволяет
обратить внимание ученика на суть данного
математического понятия. (Пример: переместительное
свойство сложения и умножения 1 кл. ч. 2, стр.8; 2 кл., ч.1, стр.100)
15. Отличительная особенность курса математики УМК «ПНШ»
• Практическая направленность: привведении новых понятий анализируется
реальная правдоподобная ситуация
(Пример: знакомство с понятием площади 3кл. Стр.52,53)
• Прикладной характер текстовых
сюжетных задач, которые можно
решить опираясь на те понятия и
умения, которые узнали раньше (Пример: 3кл.
Стр.78)
16. Методическое основание курса математики УМК «ПНШ»
• Рассмотрение традиционных вопросовс использованием нетрадиционных
подходов (чему учить и как учить?).
• Традиционный перечень вопросов
рассматриваемый нетрадиционным
способом
• Научный подход к изучению предмета
(принцип научности). (Пример: изучение чисел
первого десятка в учебниках М.И.Моро 2 кл.стр.46 - понятие
«произведение»)
17. УМК «Перспективная начальная школа»
• Изучение арифметического материалаостается стержнем всего курса,
осуществляется с возможным паритетом
теоретической и прикладной составляющих,
а в вычислительном плане особое внимание
уделяется способам и технике устных
вычислений.
• Особенностью изучения арифметических
действий в настоящем курсе является
строгое следование математической сути
этого понятия (действие сложения вводится
после знакомства с числами от 1 до 5).
18. Арифметическая линия
• Изучение чисел- Натуральные числа от 1 до 10 и число 0 (1-е
полугодие 1-го класса);
- От 0 до 20 (2-е полугодие 1-го класса);
- Целые числа от 0 до 100 и «круглые» числа
до 1000 (2-й класс);
- Целые числа от 0 до 999999 (3-й класс);
- Целые числа от 0 до 1000000 и дробные
числа (4-й класс)
19. Арифметическая линия
• Числа от 1 до 5 и число 0 изучаются наколичественной основе.
• Числа от 6 до 10 на аддитивной основе
с опорой на число 5.
• Числа второго десятка и все остальные
натуральные числа изучаются на
основе принципов нумерации
(письменной и устной) десятичной
системы счисления.
20. Число 1
Это число должно восприниматься
детьми, как количественная
характеристика единичного объекта.
Число 1 является, с одной стороны,
базой для построения всех других
чисел, с другой – несет на себе
философскую нагрузку (нет
абсолютно одинаковых предметов,
каждый индивидуален и
представлен в единственном
числе).
Совокупность из нескольких
единичных предметов – новая
количественная реальность.
(Именно такой взгляд на
окружающую действительность
нашел отражение в канторовской
теории множеств)
См.стр.24,25,26,27
21. Число 0
• Это число рассматриваетсякак численность пустого
множества, т.е. число ,
которое позволяет ответить
на вопрос: сколько у нас
имеется того, чего у нас нет?
Объяснять ребенку суть
пустого множества
предлагается на основе
противопоставления с
единичным множеством,
которое является непустым
• См.стр.30,31,32,33
22. Числа 2,3,4,5
• Эти числа вводятся по однойсхеме, сначала детям
предлагается рассмотреть
ситуацию, в которой
фигурирует множество,
жестко количественно
связано с данным числом
(эталонное множество): 2крылья птицы,3-тройка
лошадей,4-лапы у кошки,5пальцы на руке.
• Каждое из этих чисел
предлагается рассматривать
как единый образ.
• См.стр.35,36,40,46,50
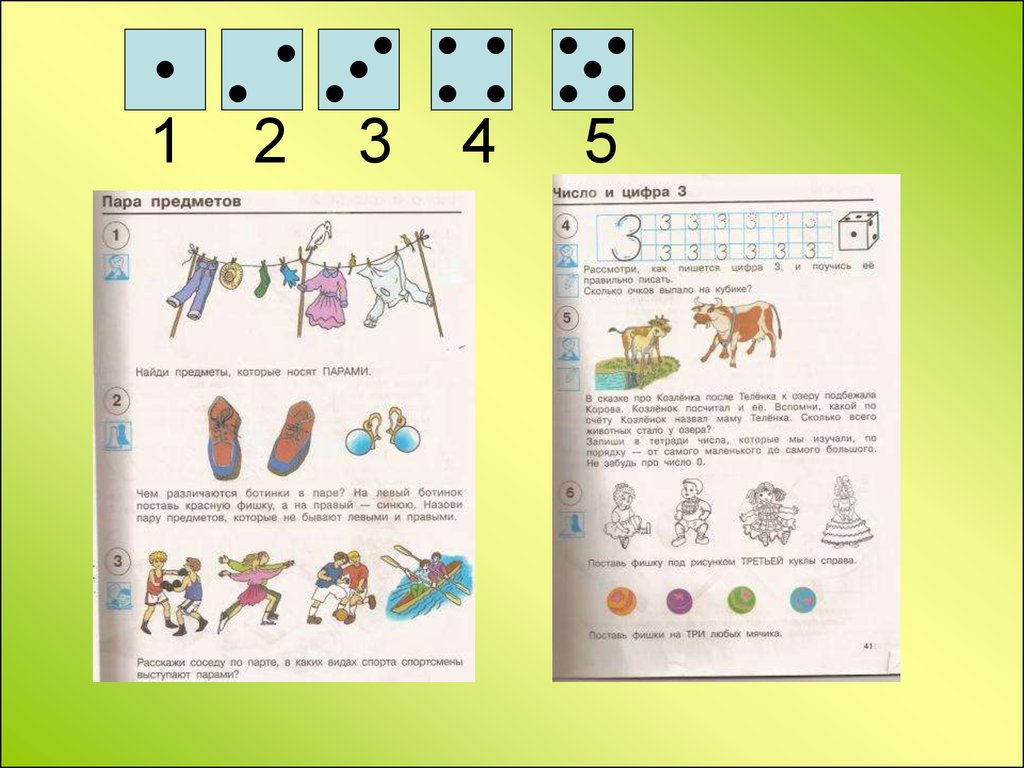
23. 1 2 3 4 5
24. Числа то 6 до 9
• Их возникновениеимеет аддитивную
природу, т.е. основано
на сложении.
• Поэтому сначала на
множестве изученных
чисел (0,1,2,3,4,5,)
вводится операция
сложения (объединение
непересекающихся
множеств).
• Стр. 58,62,66,70
25. 6 7 8 9 10
67
8
Новое число получается как
результат сложения числа 5 с
числами 1,2,3,4,5 и
рассматривается как
численность соответствующих
множеств, жестко связанных с
этим числом. (стр.58,62,66,70)
Такой подход согласуется
во-первых, с понятной и
доступной процедурой счета на
пальцах;
во-вторых, готовит детей к
введению чисел второго
десятка, только роль числа 5
будет выполнять число10;
в-третьих, дает нам
возможность в дальнейшем
обогатить арсенал приемов
устных вычислений
8+6=(5+3)+(5+1)=(5+5)+(3+1)=
=10+4=14
9
10
26. Порядковые числа
• Параллельно с введением чисел наколичественной основе предлагается
детям усвоить и порядковые
числительные, привлекая героев сказки
«про Козленка, который умел считать
до десяти».(см.методич.пособ.стр.11)
• См. 1 кл.,ч.1, стр.27,37,41,47,51,59,77
27. Действия над числами (действие сложения)
Теоретическая основаобъединение
непересекающихся множеств (в
логике подачи материала и в
подходе к построению и анализу
соответствующей ситуации)(52)
Сложение – это операция над
числами: кроме двух чисел,
которые нужно сложить, должно
присутствовать и третье число,
которое получится в результате
сложения. Если нет результата,
то нет и действия.
Сложение - объединение двух
множеств. В результате
сложения должно получиться
число, которое будет являться
количественной
характеристикой объединения
непересекающихся множеств.
28. Действия над числами
• После введения действия сложенияможно говорить о сумме чисел как о
записи , в которой указывается , что над
данными числами нужно выполнить
действие сложения; о слагаемых как о
числах, которые нужно сложить, и о
значении суммы как о числе, которое
получается в результате сложения
данных чисел. (1кл.,ч.1, стр.54,55)
29. Действия над числами действие вычитания
• Теоретическая основа – «вычитание подмножества»(связана с использованием диаграмм Эйлера-Венна
для моделирования соответствующей ситуации.)
• Вычитание-это операция над числами : кроме числа,
которое вычитают, должно обязательно
присутствовать и третье число, которое получается в
результате вычитания. Нет результата, то нет и
действия!
• В основу вычитания чисел положено вычитание
множества из подмножества
Стр.80,81
30. Действия сложения и вычитания
• В дальнейшем сложения и вычитанияосуществляются параллельно.
• Теоретическое обоснование – взаимосвязь
между этими действиями
• Сложение и вычитание изучается по двум
направлениям:
- Изучение различных свойств этих операций;
- Совершенствование вычислительных умений
учащихся за счет изучения «новых» способов
вычислений
31. Сложение и вычитание
• Тесная связь между этими действиями: с однойстороны, вычитая из значения суммы одно из
слагаемых, мы получаем другое слагаемое, а с
другой, - прибавляя к значению разности
вычитаемое, мы получаем уменьшаемое. В этом и
состоим взаимообратность операций сложения и
вычитания. Значимость данного свойства
объясняется тем, что , во-первых, на его основе
можно обучать учащихся выполнять вычитание; вовторых, на основе этого свойства учащиеся в
дальнейшем будут формулировать правила
нахождения неизвестного слагаемого и неизвестного
уменьшаемого; в-третьих, это свойство можно
использовать для проверки правильности
выполнения действий сложения и вычитания.
32. Свойства сложения и вычитания
33. Просчеты при планировании уроков УМК «ПНШ»
• В подборе содержания урока (основной недочет –привлечение дополнительных материалов и
использование организационных форм, не
запланированных учебником и , как показала практика
работы, не способствующих реализации предусмотренных
в УМК внутрипредметных и межпредметных связей );
• В логике подачи нового материала (основной недочет –
учитель не придерживается методики объяснения нового
материала, предложенной учебником. Тем самым не
реализуется прием пошагового предъявления нового
материала, рассчитанный на самостоятельное открытие
детьми правила, закономерности или причин того или
другого явления).
• В организации урока (основной недочет – увлечение
формами работы, переоценка значимости которых
приводит к снижению детской активности и
самостоятельности при формировании общих учебных
умений, навыков и способов деятельности)
• Субъектно-объектные отношения (учитель-ученик)
34.
Дидактические задачи урокаОсновные дидактические (обучающие ) задачи урока
Обеспечение осознания и усвоения понятий, законов, правил, алгоритмов,
закономерностей (усвоение =понимание + запонимание -- правильное
воспроизведение)
Формирование умений (навыков) применения теоретических положений
(закономерностей, понятий, законов, правил, алгоритмов) в условиях
решения учебных задач
(овладение = усвоение + применение ЗУНов в условиях решения учебных
задач)
Формирование общих учебных умений в условиях решения учебных задач
(познавательная деятельность, речевая деятельность и работа с
источником информации, организационная деятельность)
(овладение = усвоение + применение общих учебных умений в условиях
решения учебных задач)
Формирование общих учебных умений в условиях решения практических
задач
(овладение = усвоение общих учебных умений + применение ЗУНов по
математике в условиях решения практических задач)
Повторение (обобщение или систематизация )знаний, умений, навыков
Контроль за степенью усвоения ЗУНов
35. Каждому ученику должна быть предоставлена возможность:
•поработать с текстом учебника (поупражняться всамообразовании);
• самостоятельно поработать над учебным заданием
(возможна помощь со стороны учителя или соседа по
парте, учитывается мера помощи);
•поупражняться в коммуникативной деятельности;
•поупражняться в приемах мыслительной деятельности
(анализ, синтез, сравнение, обобщение, классификация и
т.д.);
•поупражняться в целеполагании.
•дать самооценку своей деятельности на уроке,
поупражняться в приеме самоконтроля, самооценке
взаимоконтроля и взаимооценке;
•поупражняться в способности понимать текст,
содержащий нужную информацию; текст, содержащий
нормативную информацию (инструкцию);
•поупражняться в речевой деятельности.
36. Алгоритмическая линия (решение арифметических сюжетных задач)
• Курс математики имеет прикладнуюнаправленность (умение применять
полученные знания на практике)
• Важно не только научить решать задачи, но и
правильно формулировать их.
• Под решением задачи понимается запись
(описание) алгоритма, дающего возможность
выполнить требование задачи (получение
ответа задачи относится прежде всего к
области вычислительных умений)
37.
38. Описание алгоритма решения задачи
1. По действиям (по шагам) спояснениями;
2. В виде числового выражения, которое
рассматривается, как свернутая
форма описания по действиям, но без
пояснений;
3. В виде буквенного выражения (в
некоторых случаях в виде формулы
или в виде уравнения)
39. Формирование умения решать задачи
1.2.
Учащиеся должны научиться работать с текстом и
иллюстрациями: определить, является ли текст задачей,
установить связь между данными и искомым, определить
последовательность шагов по установлению значения
искомого.
Проведение различных преобразований текста и наблюдение
за теми изменениями в ее решении , которые возникли в
результате этих преобразований: дополнение текстов до
задачи, представление одной и той же задачи в разных
формулировках; упрощение или усложнение исходной
задачи; поиск особых случаев изменения исходных данных,
приводящих к упрощению решения; установление задач,
которые можно решить при помощи уже решенной задачи,
что в дальнейшем становится основой классификации задач
по сходству математических отношений, заложенных в них.
40. Обучение решению задачи Методические подходы:
• Традиционные: составление краткой записи;• Нетрадиционные: моделирование с помощью
схемы, составленной на основе диаграммы
Эйлера-Венна; графическое моделирование
(диаграммы сравнения); составление краткой
записи в виде таблицы; схемы, на которой
каждая из двух неизвестных величин
изображается в виде полосы определенной
длины (полосы расположены так, что
образуют общую полосу, которая образует
сумму этих величин).
41. Краткая запись задачи
42. Схемы
43. Таблица и краткая запись задачи
• Такая форма записи имеетцелый ряд преимуществ:
- Запись в виде таблицы
более системна и
информативна;
- Учащиеся постоянно учатся
работать с таблицей;
- Учащиеся готовятся к
использованию таблицы при
осуществлении краткой
записи с
пропорциональными
величинами;
- Таблица – пропедевтика
изучения функциональной
зависимости
44. Круговые схемы. Составные задачи на сложение и вычитание
45. Графическое моделирование (диаграмма сравнения)
• Диаграмма сравненияустроена так, что в ее
конструкции задействован
луч, что позволяет готовить
учащихся к изучению
системы координат;
• Диаграммы сравнения – это
очень востребованный в
настоящее время
графический способ
представления числовых
данных (диаграммы можно
видеть на экранах
телевизора, в периодической
печати и т.д.);
• С помощью диаграмм
сравнения можно наглядно
представить как процедуру
увеличения, так и процедуру
уменьшения в несколько раз
46. Задачи с недостающими и избыточными данными
-
-
Это направление в работе с
понятием «задача» связано с
проведением различных
преобразований имеющего
текста и наблюдением за теми
изменениями в ее решении,
которые возникают в результате
этих преобразований.
Различные способы получения
недостающих данных:
действия, связанные с
получением недостающих
данных путем счета или
измерения;
Действия, которые заключены в
получении необходимой
информации из дополнительных
источников
47. Задачи, в которых известен результат сравнения
• Разностное сравнение • Кратное сравнение48. Задачи на куплю-продажу, на движение и на работу
• Изучение зависимостимежду величинами
(прямопропорциональный
характер);
• Математическая природа
таких величин, как «цена»,
«скорость»,
«производительность »
единая;
• Задачи на куплю-продажу, на
движение, и на работу
рассматриваются с опорой
на аналогию (общая
математическая сущность)
• Правильное употребление
терминов и наименований
















































 education
education








