Similar presentations:
Исследование функций методами дифференциального исчисления. Условие постоянства функции
1.
§19. Исследование функцийметодами
дифференциального
исчисления
п.1. Условие постоянства функции.
2.
Теорема 1. Для того, чтобы функция y f (x),дифференцируемая на X, была
постоянной на X, необходимо и
достаточно, чтобы
f ' ( x) 0 x X .
3.
Доказательство.Необходимость.
f ( x) C x X
f ' ( x) 0
Достаточность.
f ' ( x) 0 x X
Теорема
x0 X
Лагранжа (§9)
f ( x) f ( x0 ) f ' (c)( x x0 ) c ( x; x0 )
c ( x0 ; x)
f ( x) f ( x0 ) 0 f ( x) f ( x0 ) x X
4.
п.2. Монотонность функции.Теорема 2. (Достаточное условие
монотонности)
Пусть
функция y f (x) дифференцируема на
интервале (a; b),
f ' ( x) 0 x (a; b)
f ' ( x) 0 x (a; b) .
Тогда
функция y f (x) возрастает (убывает) на
интервале (a; b).
5.
Доказательство.f ' ( x) 0 x (a; b)
x1, x2 (a, b) x1 x2
Теорема Лагранжа §9
f ( x2 ) f ( x1) f ' (c) ( x2 x1), c ( x1; x2 )
0
0
f ( x2 ) f ( x1) 0
f ( x2 ) f ( x1)
функция y f (x) возрастает на
интервале (a; b).
6.
Самостоятельно: доказать теорему в случаеубывания функции.
7.
п.3. Локальный экстремум.Точка x0 называется точкой локального
максимума функции y f (x) , если
существует некоторая окрестность точки x0
такая, что для всех x x0 из этой окрестности
выполняется неравенство
f ( x) f ( x0 ).
Самостоятельно: определить точку локального
минимума.
8.
Точки локального максимума и локальногоминимума называются точками локального
экстремума.
Теорема 3. (Необходимое условие локального
экстремума)
Пусть
функция y f (x) дифференцируема,
x0 ─ точка локального экстремума.
Тогда
f ' ( x0 ) 0.
9.
Доказательство.x0 ─ точка локального максимума
f ( x) f ( x0 ) f ( x) f ( x0 ) 0
x x0 0
f ( x) f ( x0 )
f ' ( x0 ) lim
0
x x0
x x0
x x0 0
f ( x) f ( x0 )
f ' ( x0 ) lim
0
x x0
x x0
f ' ( x0 ) 0
10.
Самостоятельно: доказать теорему в случаеточки локального минимума.
11.
Замечание 1. Необходимое условие неявляется достаточным.
y x
Пример.
y ' 3x
3
x0 0
y
2
y' ( x0 ) y' (0) 0
O
x
x0 0 не является точкой
локального экстремума
12.
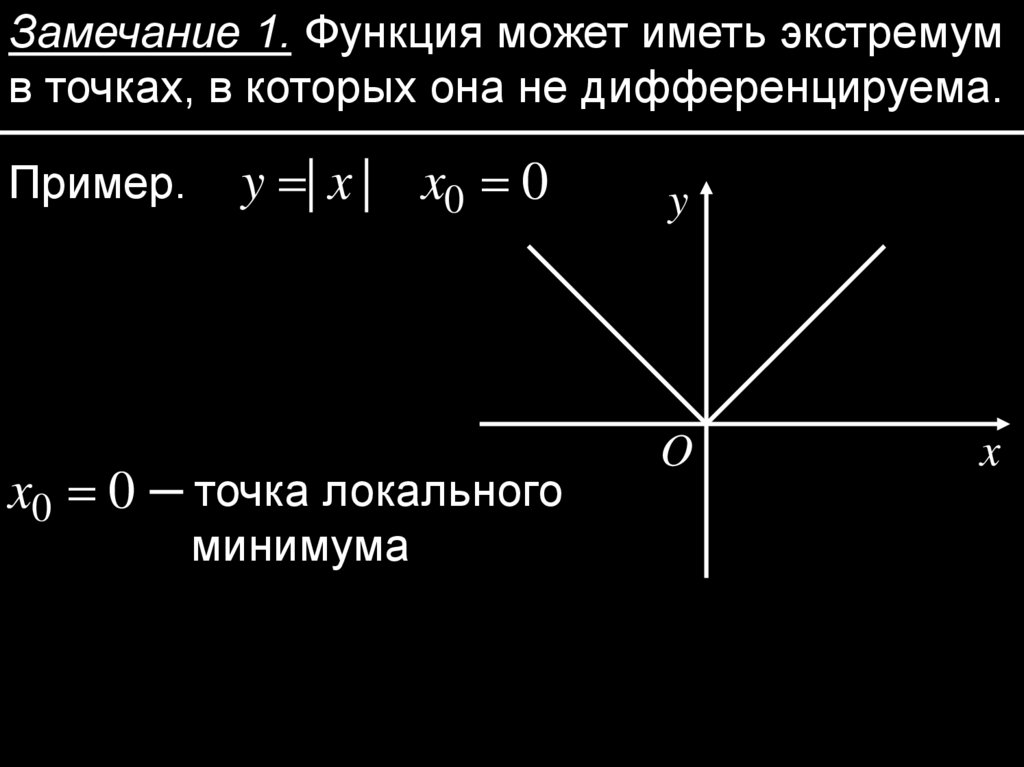
Замечание 1. Функция может иметь экстремумв точках, в которых она не дифференцируема.
Пример.
y | x | x0 0
x0 0 ─ точка локального
минимума
y
O
x
13.
Пример. yy'
3
x
2
x0 0
y
2
33 x
x0 0 ─ точка локального
минимума
O
x
14.
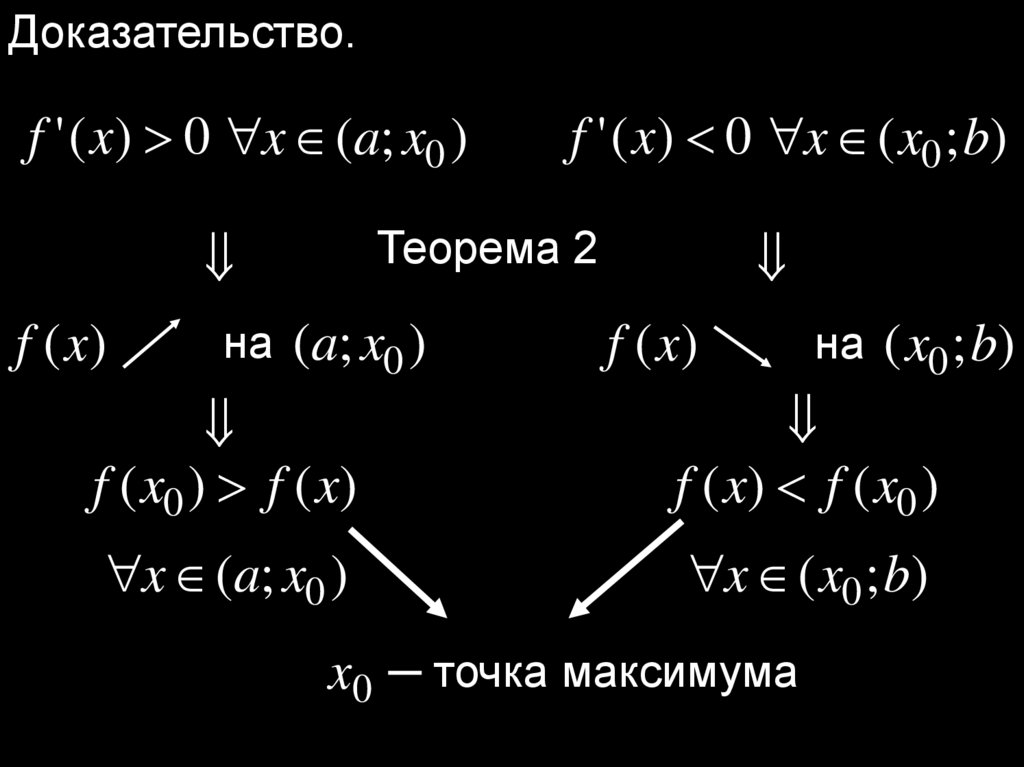
Теорема 4. (Первое достаточное условиелокального экстремума)
Если при переходе через точку x0
производная дифференцируемой
функции y f (x) меняет знак с плюса на
минус, то x0 ─ точка максимума, а если с
минуса на плюс, то x0 ─ точка минимума.
15.
Доказательство.f ' ( x) 0 x (a; x0 )
Теорема 2
f (x)
f ' ( x) 0 x ( x0 ; b)
на (a; x0 )
f (x)
на ( x0 ; b)
f ( x0 ) f ( x)
f ( x) f ( x0 )
x (a; x0 )
x ( x0 ; b)
x0 ─ точка максимума
16.
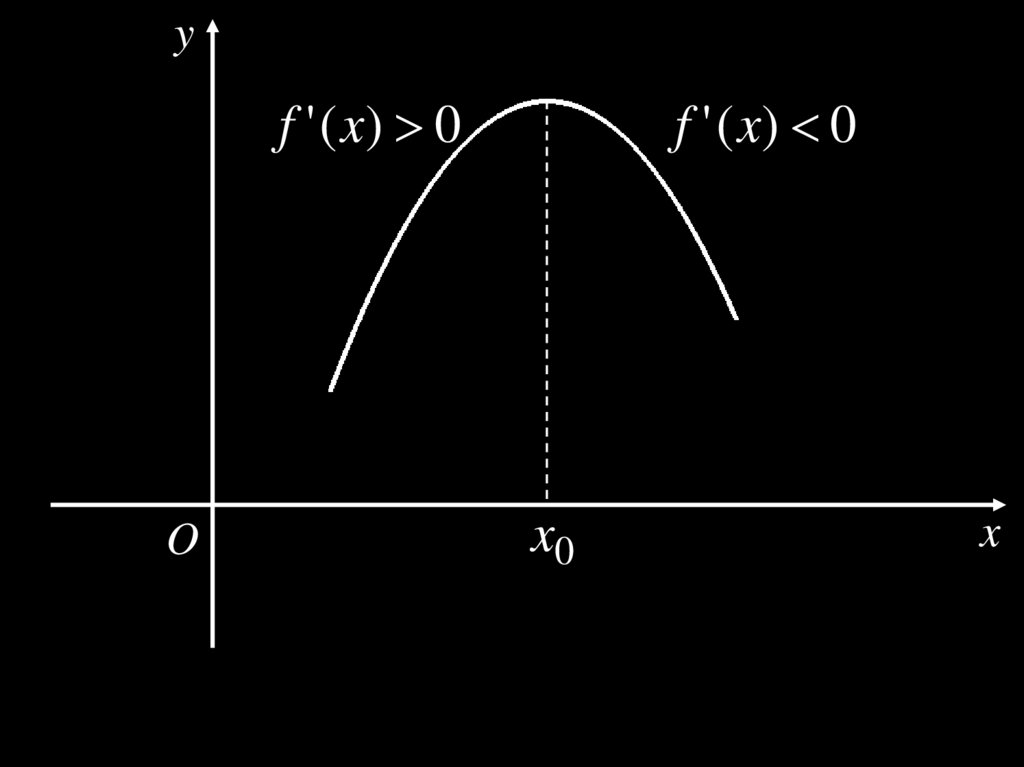
yf ' ( x) 0
O
f ' ( x) 0
x0
x
17.
Самостоятельно: доказать теорему в случаеточки минимума.
18.
Теорема 5. (Второе достаточное условиелокального экстремума)
Пусть
f ' ( x0 ) 0,
f ' ' ( x0 ) 0.
Тогда,
если f ' ' ( x0 ) 0, то x0 ─ точка максимума;
если f ' ' ( x0 ) 0, то x0 ─ точка минимума.
19.
Доказательство.f ' ( x0 x) f ' ( x0 )
f ' ' ( x0 ) lim
x 0
x
f ' ( x0 ) 0
f ' ( x0 x)
f ' ' ( x0 ) lim
x 0
x
f ' ' ( x0 ) 0 : x 0 f ' ( x0 x) 0
x 0 f ' ( x0 x) 0
Теорема 4
x0 ─ точка минимума
20.
Самостоятельно: доказать теорему в случаеточки максимума.
21.
п.4. Наибольшее и наименьшеезначение функции на отрезке.
Пусть функция y f (x) непрерывна на
отрезке [a; b].
По теореме Вейерштрасса она достигает на
этом отрезке своего наибольшего и
наименьшего значения.
Эти значения функция может принимать либо
во внутренней точке отрезка, либо на его
границе.
22.
Алгоритм поиска наибольшего инаименьшего значения функции
1. Найти критические точки (точки, в которых
производная функции равна нулю или не
существует) на интервале (a; b).
2. Вычислить значения функции в найденных
критических точках и на концах отрезка.
3. Среди вычисленных значений выбрать
наибольшее и наименьшее.
23.
п.5. Выпуклость (вогнутость) графикафункции.
Пусть
функция y f (x) дифференцируема на
интервале (a; b).
Тогда
в каждой точке ее графика существует
касательная.
24.
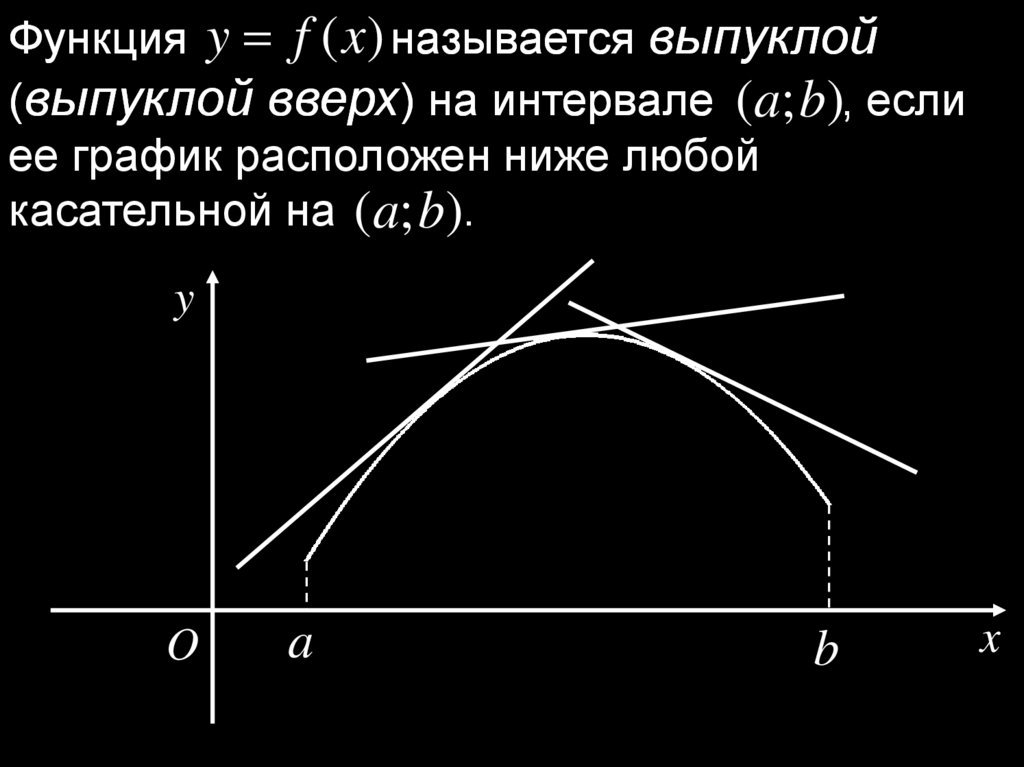
Функция y f (x) называется выпуклой(выпуклой вверх) на интервале (a; b), если
ее график расположен ниже любой
касательной на (a; b).
y
O
a
b
x
25.
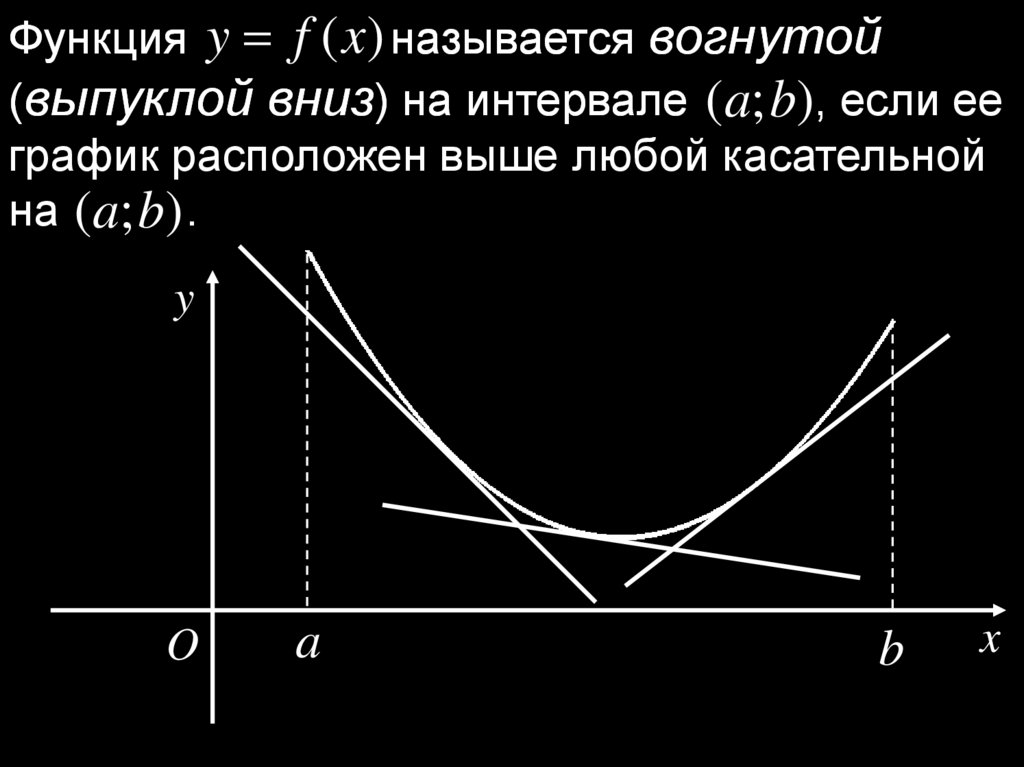
Функция y f (x) называется вогнутой(выпуклой вниз) на интервале (a; b), если ее
график расположен выше любой касательной
на (a; b) .
y
O
a
b
x
26.
Теорема 6. (Достаточное условие выпуклости)Пусть
функция y f (x) имеет вторую производную
на интервале (a; b);
f ' ' ( x) 0 x (a; b)
f ' ' ( x) 0 x (a; b) .
Тогда
функция y f (x) выпукла (вогнута) на
интервале (a; b).
27.
Доказательство.f ' ' ( x) 0 x (a; b)
x0 (a; b) §10 п.2
0
1
2
f ( x) f ( x0 ) f ' ( x0 )( x x0 ) f ' ' (c)( x x0 )
2
c ( x0 ; x) c ( x; x0 )
f ( x) f ( x0 ) f ' ( x0 )( x x0 )
yкас f ( x0 ) f ' ( x0 )( x x0 )
f ( x) yкас
28.
Самостоятельно: доказать теорему в случаевыпуклой функции.
29.
п.6. Точки перегиба.Точкой перегиба графика непрерывной
функции называется точка, если слева и
справа от нее функция имеет разные
направления выпуклости.
30.
Теорема 7. (Необходимое условие точкиперегиба)
Пусть
функция y f (x) дважды дифференцируема;
x0 ─ точка перегиба.
Тогда
f ' ' ( x0 ) 0.
31.
Замечание 3. Необходимое условие неявляется достаточным.
Пример.
y x
4
x0 0
y' 4 x
2
y' ' 12 x
y' ' ( x0 ) y' ' (0) 0
y
3
x0 0 не является точкой
перегиба.
O
x
32.
Замечание 4. Точки перегиба ─ это точкиэкстремума первой производной функции.
33.
Теорема 8. (Достаточное условие точкиперегиба)
Если при переходе через точку x0 вторая
производная дважды дифференцируемой
функции y f (x) меняет знак, то x0 ─ точка
перегиба.
y
3
Пример. y x
y ' 3x y ' ' 6 x
y ' ' 0 x ( ;0)
y ' ' 0 x (0; )
x0 0 ─ точка перегиба
2
O
x
34.
п.7. Асимптоты.Асимптотой кривой называется прямая,
расстояние до которой от точки, лежащей на
кривой, стремится к нулю при неограниченном
удалении от начала координат этой точки по
кривой.
35.
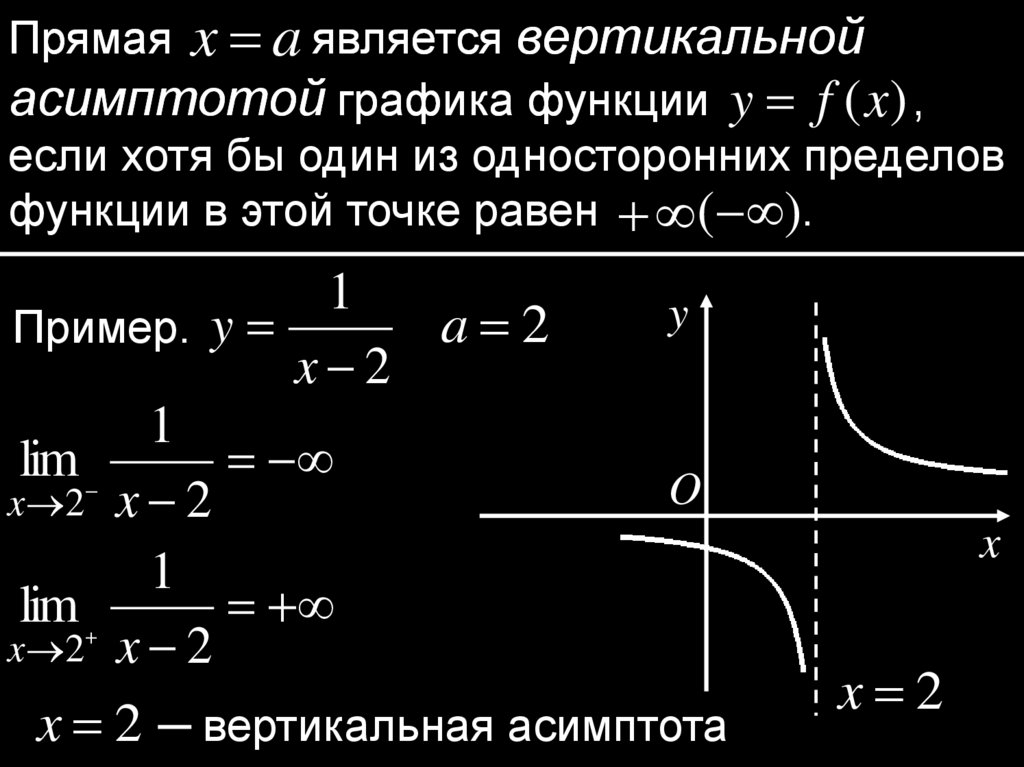
Прямая x a является вертикальнойасимптотой графика функции y f (x) ,
если хотя бы один из односторонних пределов
функции в этой точке равен ( ).
1
y
a 2
Пример. y
x 2
1
lim
O
x 2 x 2
1
lim
x 2 x 2
x 2 ─ вертикальная асимптота
x
x 2
36.
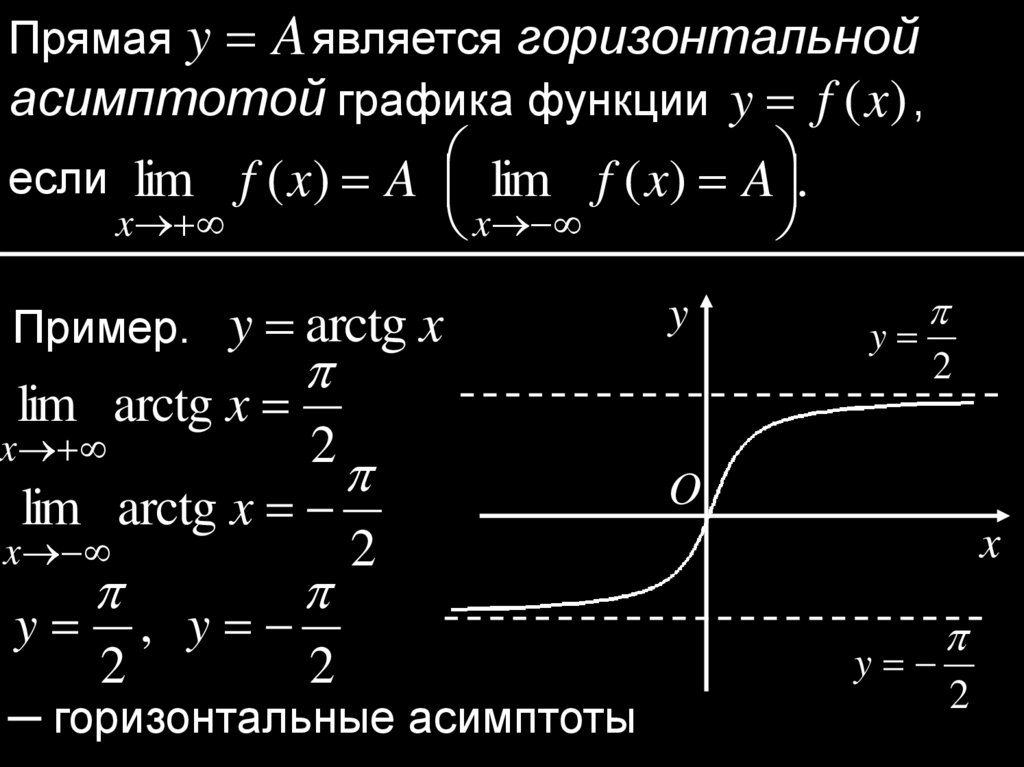
Прямая y A является горизонтальнойасимптотой графика функции y f (x) ,
если lim f ( x) A lim f ( x) A .
x
x
Пример. y arctg x
lim arctg x
x
2
lim arctg x
x
2
y
2
, y
2
─ горизонтальные асимптоты
y
y
2
O
x
y
2
37.
Уравнение наклонной асимптоты: y kx b.Теорема 9. Для того, чтобы график
функции y f (x) имел наклонную
асимптоту при x ( x )
необходимо и достаточно, чтобы
существовали конечные пределы
f ( x)
lim
k,
x x
f ( x)
k,
lim
x x
lim ( f ( x) kx) b
x
lim ( f ( x) kx) b
x
38.
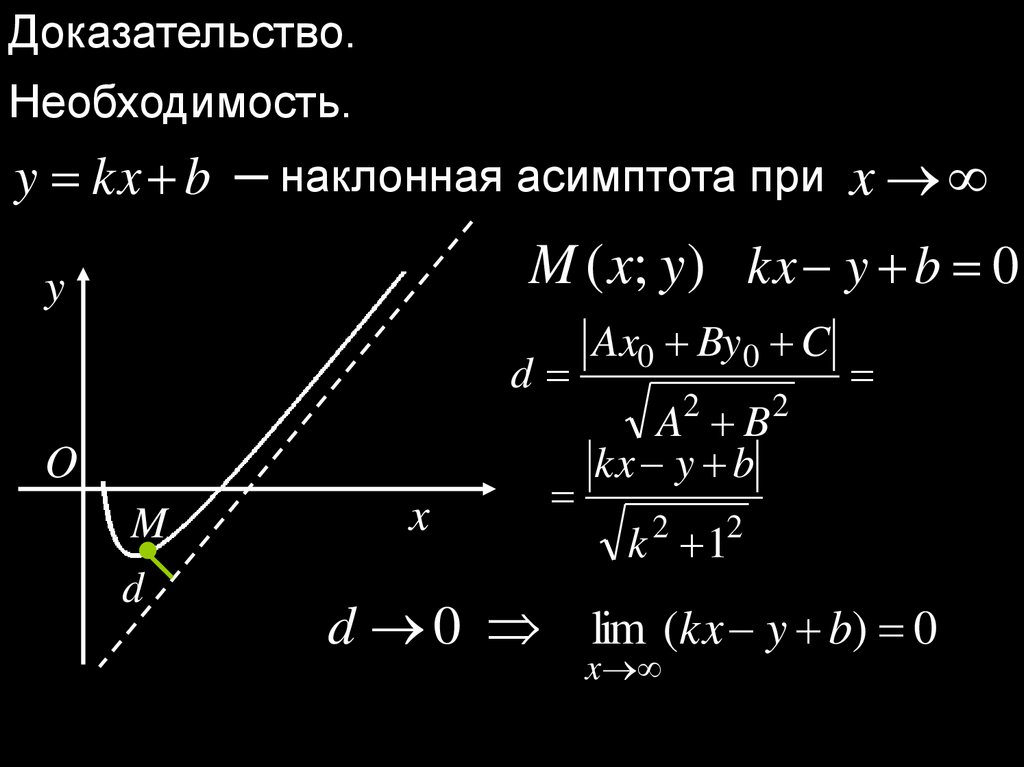
Доказательство.Необходимость.
y kx b ─ наклонная асимптота при x
M ( x; y ) kx y b 0
y
d
O
M
d
x
Ax0 By 0 C
A2 B 2
kx y b
k 2 12
d 0 lim (kx y b) 0
x
39.
Теорема 2 §6kx y b (x)
(x) ─ БМФ при x
y f ( x) kx b ( x)
f ( x)
kx b ( x)
lim
lim
k
x x
x
x
lim ( f ( x) kx) lim (b ( x)) b
x
x
40.
Достаточность.f ( x)
lim
k
x x
lim ( f ( x) kx) b
x
Теорема 2 §6
f ( x) kx b ( x)
(x) ─ БМФ при x
f ( x) (kx b) ( x)
y kx b ─ наклонная асимптота





















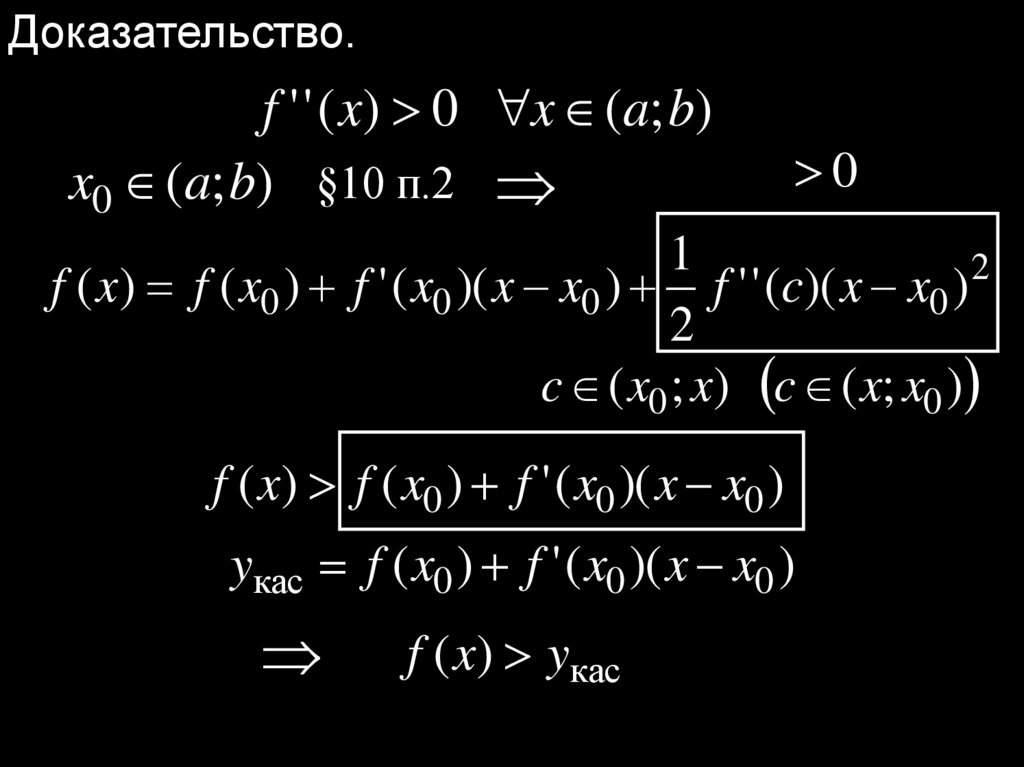








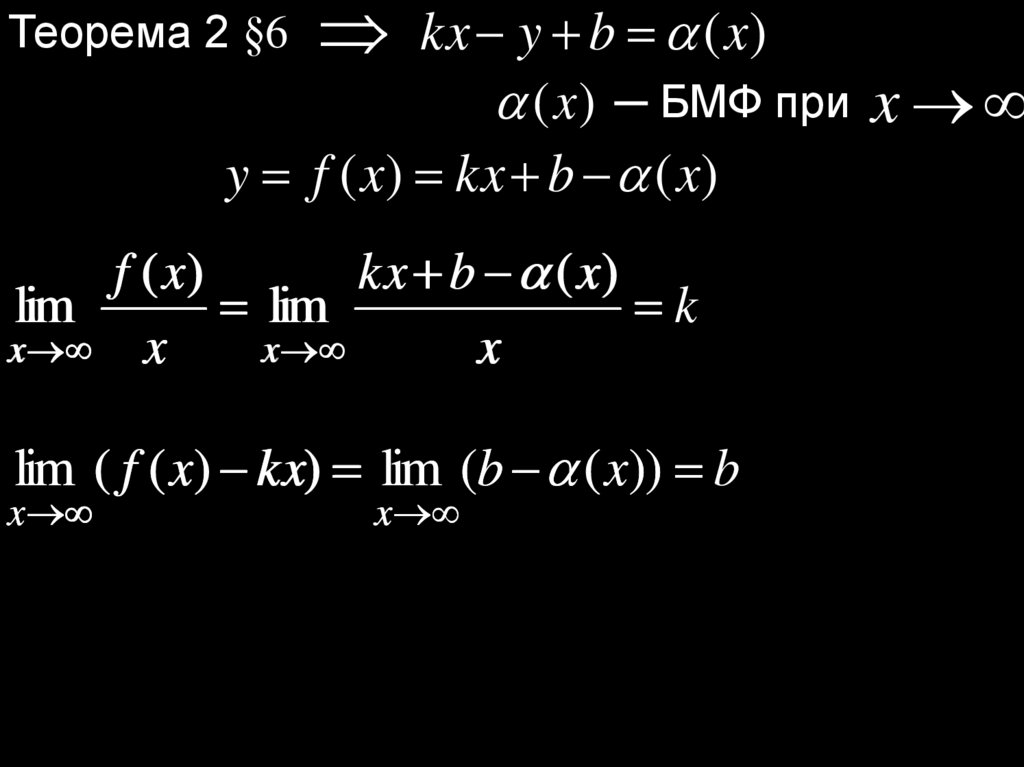

 mathematics
mathematics








