Тема 3.3 Перпендикулярность прямой и плоскости

1.

«Упорство вороны,
выдержка цапли,
чутьё и бдительность собаки,
умеренность в еде,
скромность – таковы
5 условий успеха в учёбе»
Священные писания

2.

Тема 3.3
Перпендикулярные прямая и
плоскость

3.

Перпендикулярные прямая и
плоскость
Определение:
Прямая, пересекающая плоскость, называется
перпендикулярной
плоскости,
если
она
перпендикулярна каждой прямой, лежащей в этой
плоскости. Если прямая a перпендикулярна
плоскости β, то пишут, как обычно:

4.

Свойства перпендикулярных
прямой и плоскости
Теорема 1. Если одна из двух параллельных
прямых перпендикулярна плоскости, то и другая
прямая перпендикулярна этой плоскости.

5.

Свойства перпендикулярных
прямой и плоскости
Теорема
2
(о
параллельности
прямых,
перпендикулярных плоскости). Если две прямые
перпендикулярны одной плоскости, то они
параллельны.

6.

Признак перпендикулярности
прямой и плоскости
Теорема 3 (признак перпендикулярности прямой
и плоскости). Если прямая перпендикулярна
двум пересекающимся прямым, лежащим в
плоскости, то она перпендикулярна этой
плоскости.

7.

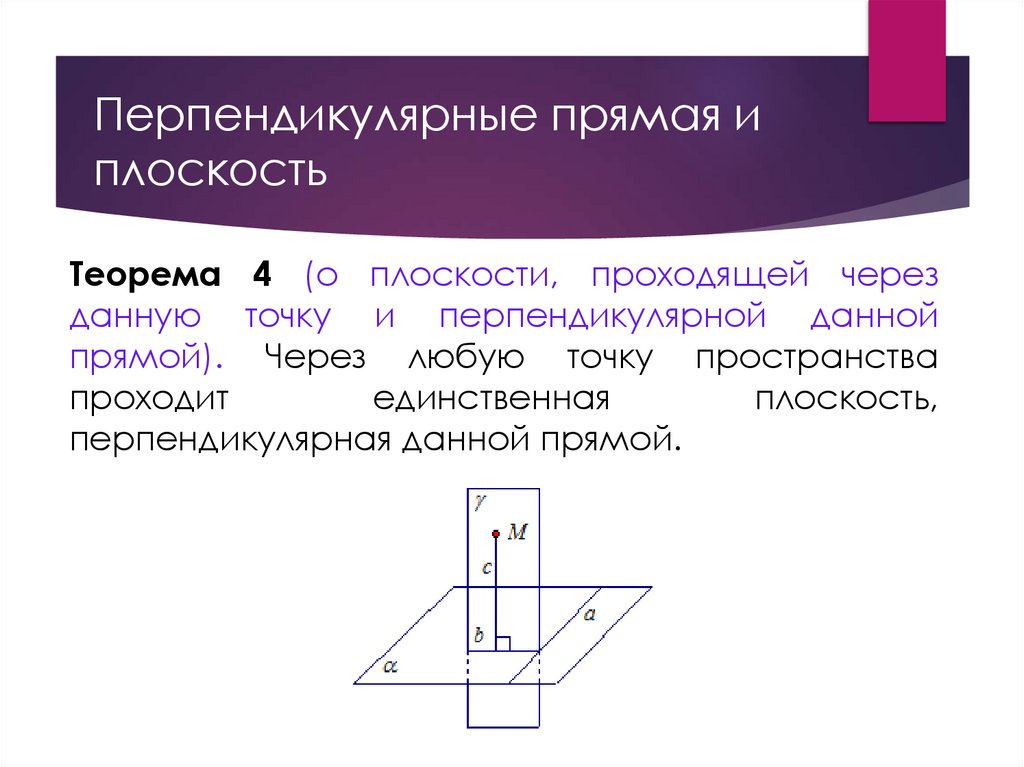
Перпендикулярные прямая и
плоскость
Теорема 4 (о плоскости, проходящей через
данную точку и перпендикулярной данной
прямой). Через любую точку пространства
проходит
единственная
плоскость,
перпендикулярная данной прямой.

8.

Перпендикулярные прямая и
плоскость
Теорема 5 (о прямой, проходящей через данную
точку и перпендикулярной данной плоскости).
Через любую точку пространства проходит
единственная прямая, перпендикулярная данной
плоскости.

9.

Тема 3.3
Задачи

10.

Докажите, что если две плоскости α и β
перпендикулярны к прямой а, то они
параллельны.
Доказательство:
Проведем прямую с параллельно прямой а. По лемме,
если одна из двух параллельных прямых пересекает
плоскость, то и другая прямая тоже пересекает плоскость.
Прямая а пересекает плоскости α и β по условию. Значит
прямая с пересекает плоскость α в некоторой точке А и
плоскость β в точке В.
Прямая а перпендикулярна плоскостям α и β, а значит и
параллельная ей прямая с перпендикулярна плоскостям
α и β.
Предположим, что плоскости α и β пересекаются.
Точка М – общая точка плоскостей α и β. Но тогда в
треугольнике АМВ угол МАВ равен 90° и угол АВМ равен
90°, что невозможно. Значит, предположение о том, что
плоскости α и β пересекаются было неверным. Значит,
плоскости α и β параллельны.

11.

Докажите, что через любую точку
пространства проходит только одна
плоскость, перпендикулярная данной прямой.
Доказательство:
Пусть дана прямая а и точка М. Согласно утверждению,
существует плоскость γ, проходящая через точку М,
перпендикулярная прямой а. Докажем ее
единственность.
Предположим, что существует плоскость γ1,
проходящая через точку М, перпендикулярная прямой
а. Две плоскости γ и γ1 перпендикулярны одной и той
же прямой а, а значит, плоскости γ и γ1 параллельны
(как мы доказали в задаче 1). Но точка М принадлежит
и плоскости γ и γ1. Получили противоречие. Значит,
через любую точку пространства проходит только одна
плоскость, перпендикулярная данной прямой а, что и
требовалось доказать.

12.

Задание: пройти тест и показать
результат
Перпендикулярные прямая и
плоскость тест:
https://onlinetestpad.com/ru/test/
627638-perpendikulyarnostpryamoj-i-ploskosti

13.

Тема 3.3
Домашняя работа

14.

Домашняя работа (обязательно к выполнению)
Решить задачи:

15.

Благодарю всех за работу!
Желаю успеха в учёбе!