Перпендикулярность прямых и плоскостей в пространстве

1. Уважаемые обучающиеся! Задание по математике на 16.05.2020. ТЕМА: Перпендикулярность прямых и плоскостей в пространстве. План

занятия:
1) Записать в тетрадь конспект (определения, теоремы +
рисунки)
2) Ответить на вопросы

2. Перпендикулярность прямых и плоскостей.

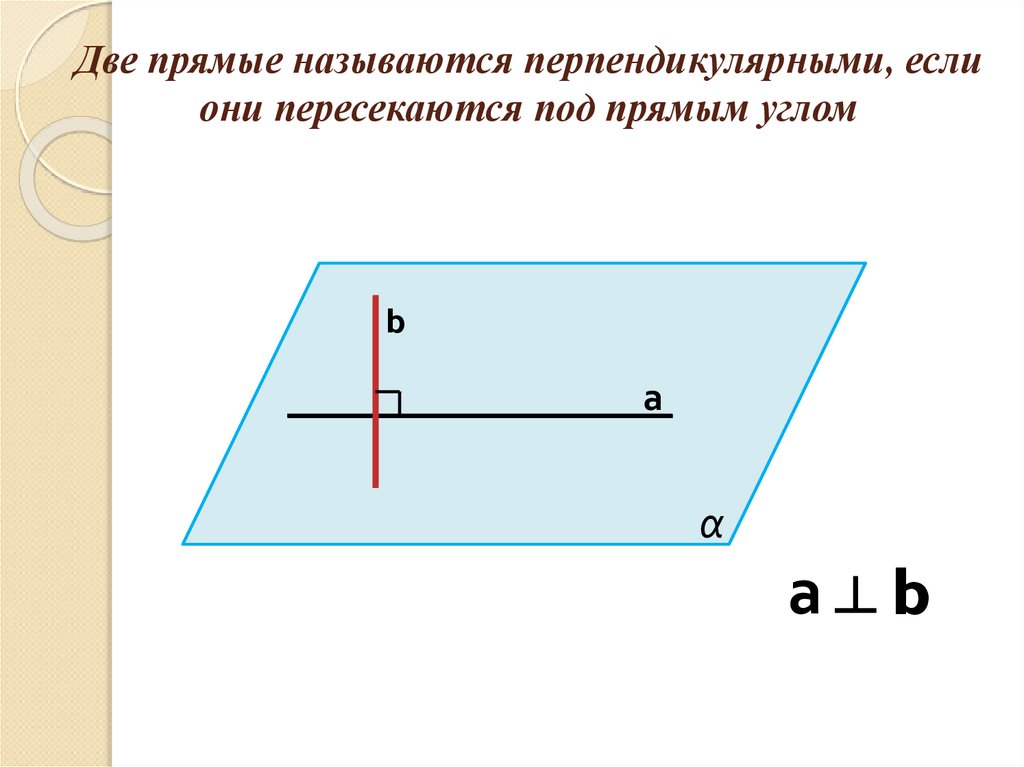
3. Две прямые называются перпендикулярными, если они пересекаются под прямым углом

b
а
α
а┴b

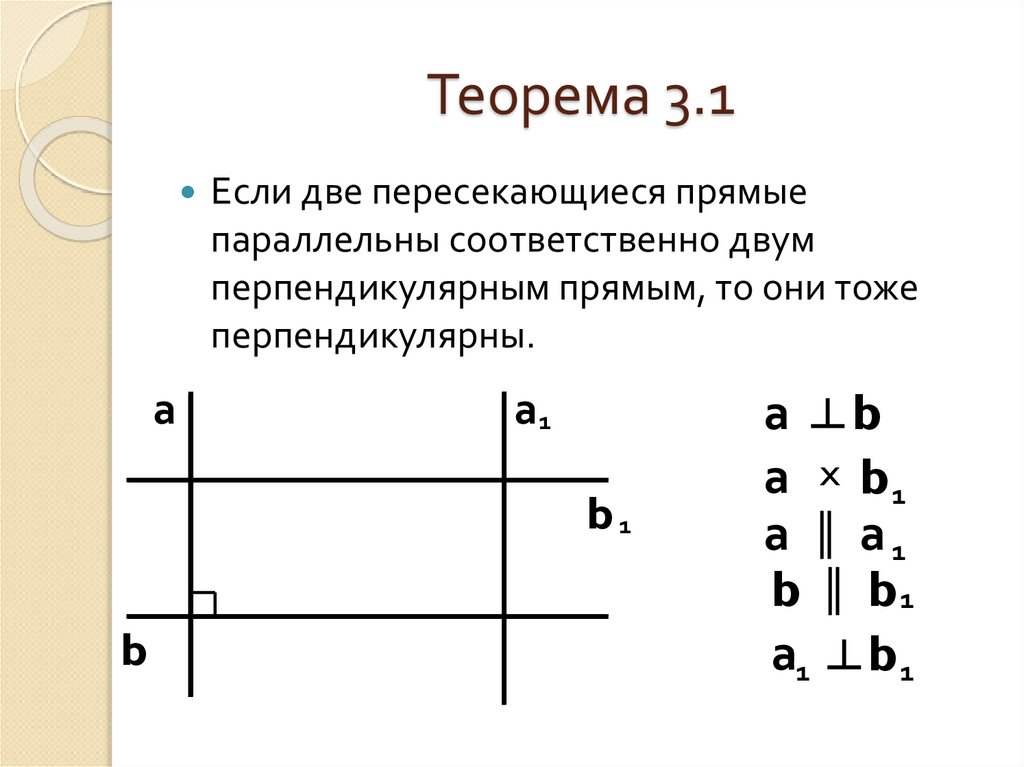
4. Теорема 3.1

а
Если две пересекающиеся прямые
параллельны соответственно двум
перпендикулярным прямым, то они тоже
перпендикулярны.
а1
b1
b
а ┴b
а X b1
а ║ а1
b ║ b1
а1 ┴ b 1

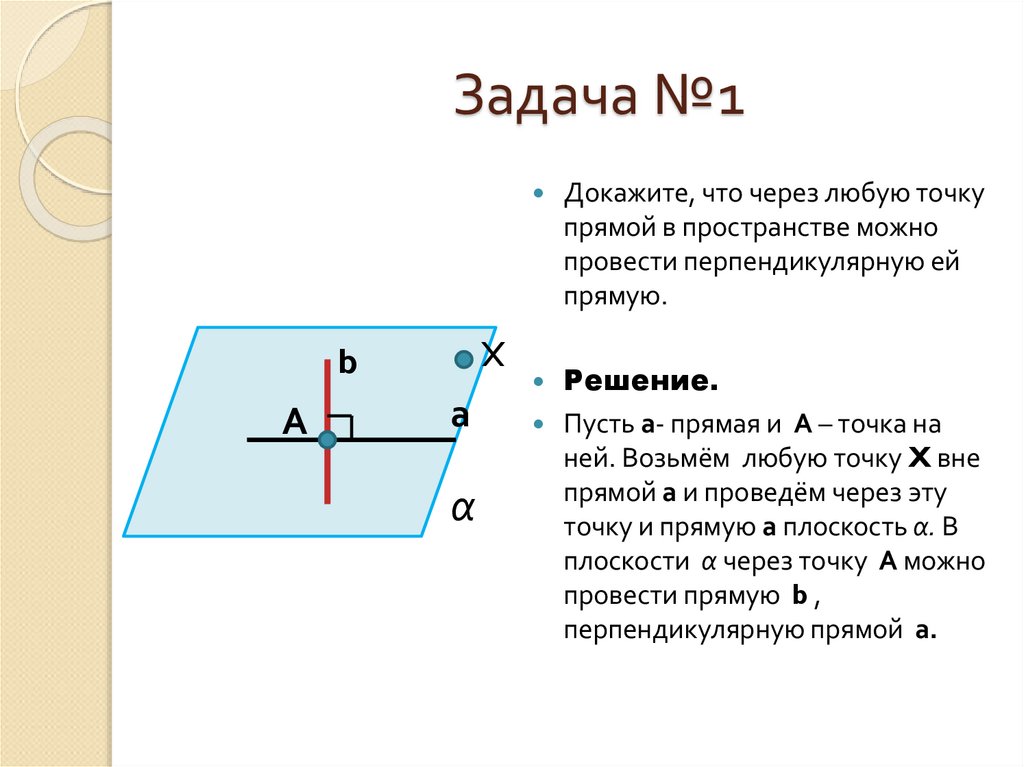
5. Задача №1

X
b
А
А
а
α
Докажите, что через любую точку
прямой в пространстве можно
провести перпендикулярную ей
прямую.
Решение.
Пусть а- прямая и А – точка на
ней. Возьмём любую точку X вне
прямой а и проведём через эту
точку и прямую а плоскость α. В
плоскости α через точку А можно
провести прямую b ,
перпендикулярную прямой а.

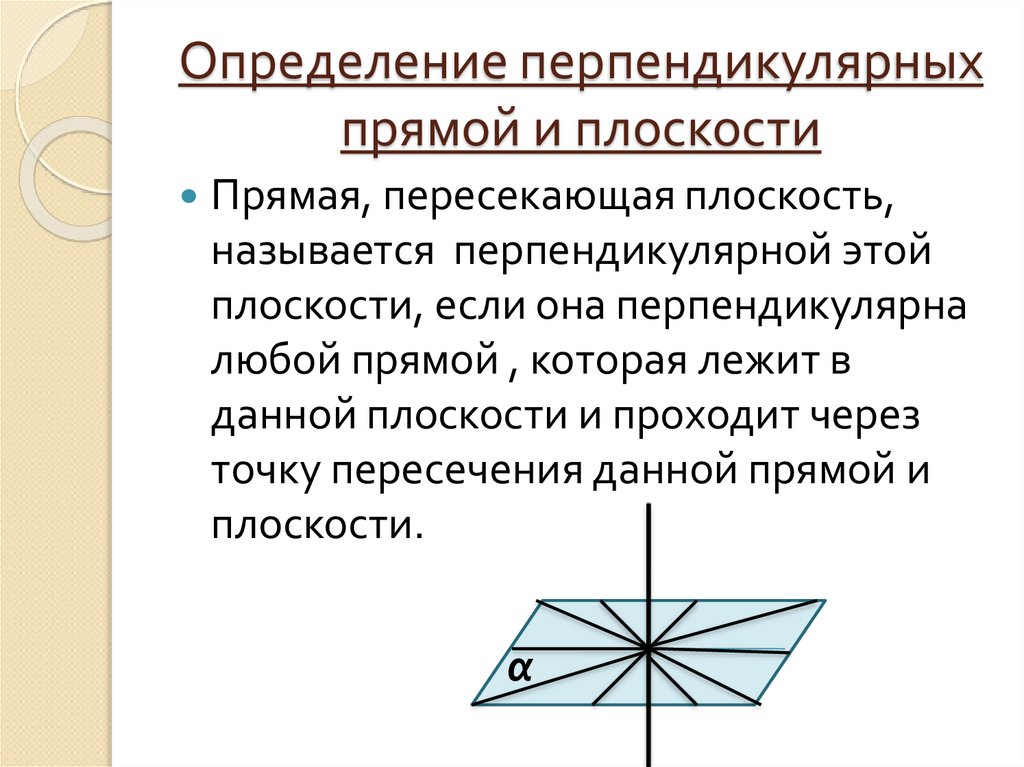
6. Определение перпендикулярных прямой и плоскости

Прямая, пересекающая плоскость,
называется перпендикулярной этой
плоскости, если она перпендикулярна
любой прямой , которая лежит в
данной плоскости и проходит через
точку пересечения данной прямой и
плоскости.
α

7. Теорема 3.2

Если прямая
перпендикулярна
двум
пересекающимся
прямым, лежащим в
плоскости, то она
перпендикулярна
данной плоскости.
а
b
C
α
а ┴ b
а ┴ C
а ┴ α

8. Свойства перпендикулярных прямой и плоскости

Теорема 3.3
а1
Если плоскость
перпендикулярна
одной из двух
параллельных
прямых, то она
перпендикулярна и
другой.
а2
α
а1 ┴ α
а1 ║ а 2
а2 ┴ α

9. Свойства перпендикулярных прямой и плоскости

Теорема 3.4
а1
а2
Две прямые,
перпендикуляр
ные одной и
той же
плоскости ,
параллельны.
α
а1 ┴ α
а2 ┴ α
а1 ║ а 2

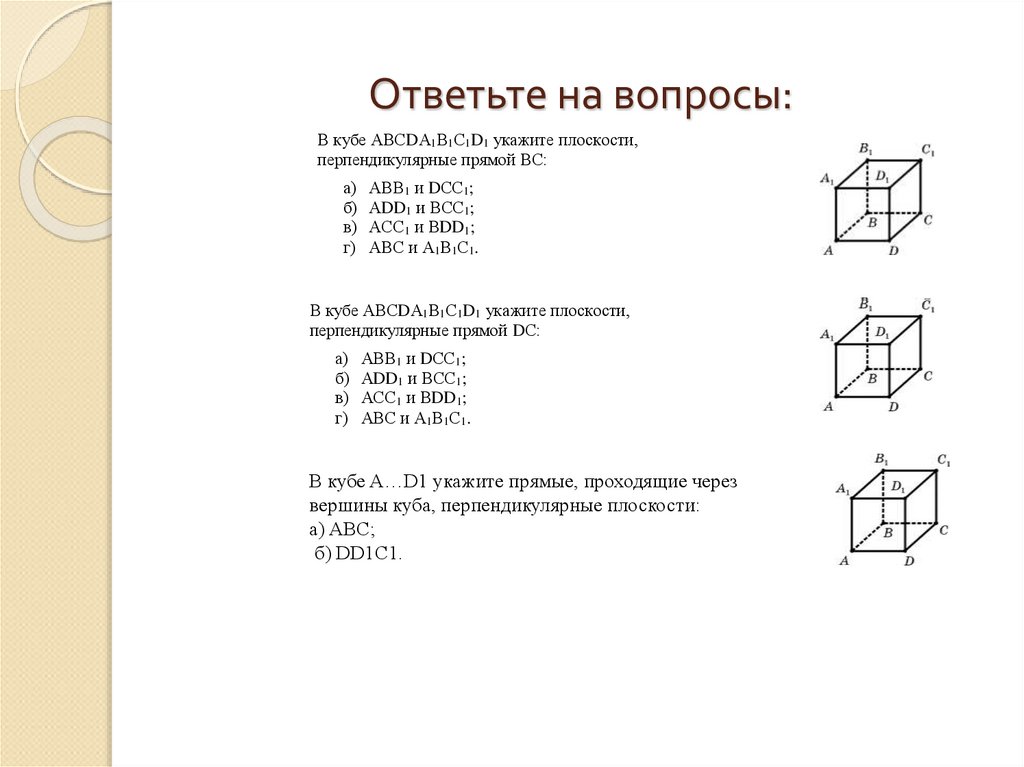
10. Ответьте на вопросы:

В кубе АВСDА1В1С1D1 укажите плоскости,
перпендикулярные прямой ВС:
а)
б)
в)
г)
АВВ1 и DСС1;
АDD1 и ВСС1;
АСС1 и ВDD1;
АВС и А1В1С1.
В кубе АВСDА1В1С1D1 укажите плоскости,
перпендикулярные прямой DС:
а)
б)
в)
г)
АВВ1 и DСС1;
АDD1 и ВСС1;
АСС1 и ВDD1;
АВС и А1В1С1.
В кубе A…D1 укажите прямые, проходящие через
вершины куба, перпендикулярные плоскости:
а) ABC;
б) DD1C1.