Similar presentations:
Определённый интеграл
1.
МатематикаПреподаватели:
Кормилицына Елена Анатольевна,
Федотова Екатерина Алексеевна
2.
Тема 12.Определённый
интеграл
3.
План лекции1. Задача о нахождении
площади криволинейной
трапеции.
2. Понятие определённого
интеграла.
4.
1. Задача о нахожденииплощади криволинейной
трапеции.
Рассмотрим задачу, которая
приводит к понятию
определённого интеграла.
В элементарной геометрии
рассматривались площади
криволинейных фигур,
5.
ограниченных прямолинейнымиотрезками, а также площадь
плоской фигуры.
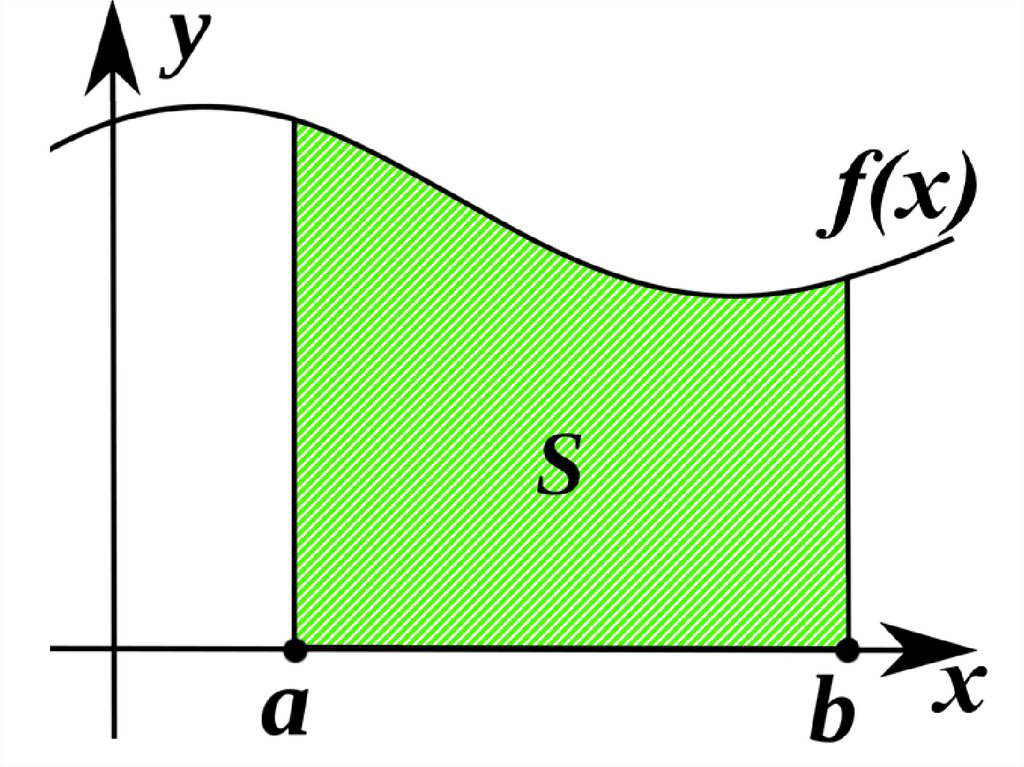
Поставим задачу о
вычислении площади S
криволинейной трапеции,
ограниченной произвольной
замкнутой линией.
6.
Опр. Криволинейной трапециейрасположенной над осью Ox
называется плоская фигура
ограниченная графиком
функции f(x) сверху, осью Ox
снизу, прямой слева x = a и
прямой справа x = b.
7.
8.
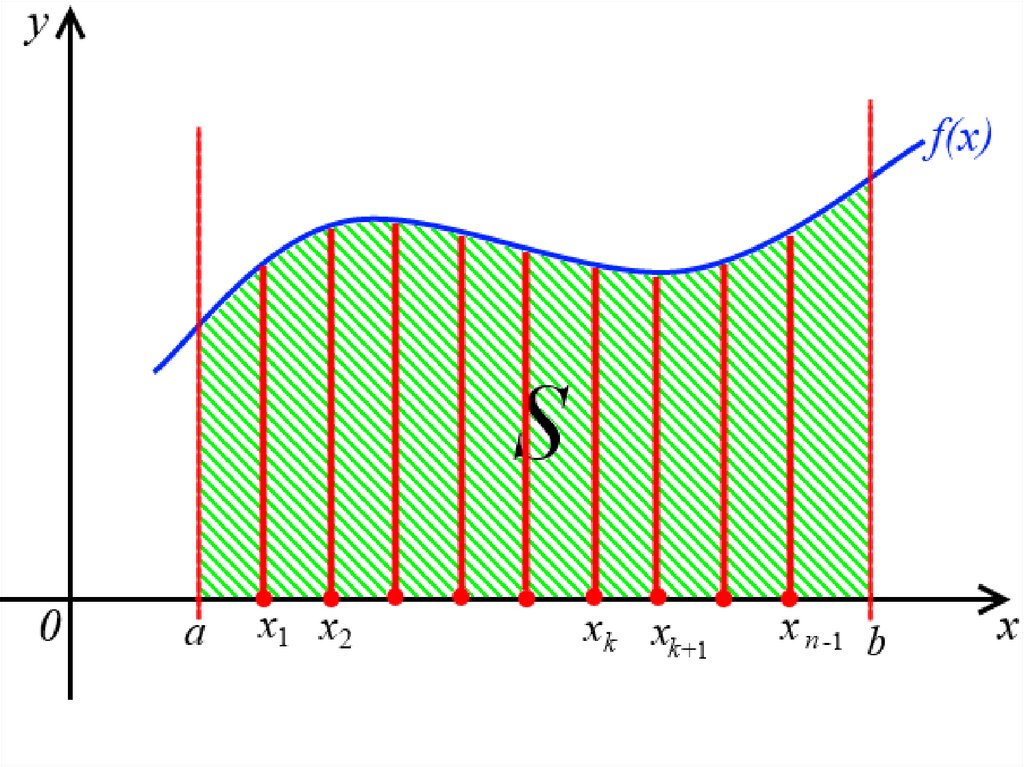
Задача: вычислить площадь Sданной криволинейной
трапеции.
Решение: Разобьём отрезок
[a;b], который является
основанием криволинейной
трапеции на n равных частей.
Данное разбиение осуществим с
помощью точек
9.
x1 , x2 , , xk , xk 1 , xn 1пологая, что
a x0 , b xn .
Проведём через эти точки
прямые параллельные оси Oy.
10.
Тогда данная криволинейнаятрапеция разобьётся на n
различных столбиков.
Площадь всей трапеции будет
равна сумме площадей всех
столбиков.
11.
12.
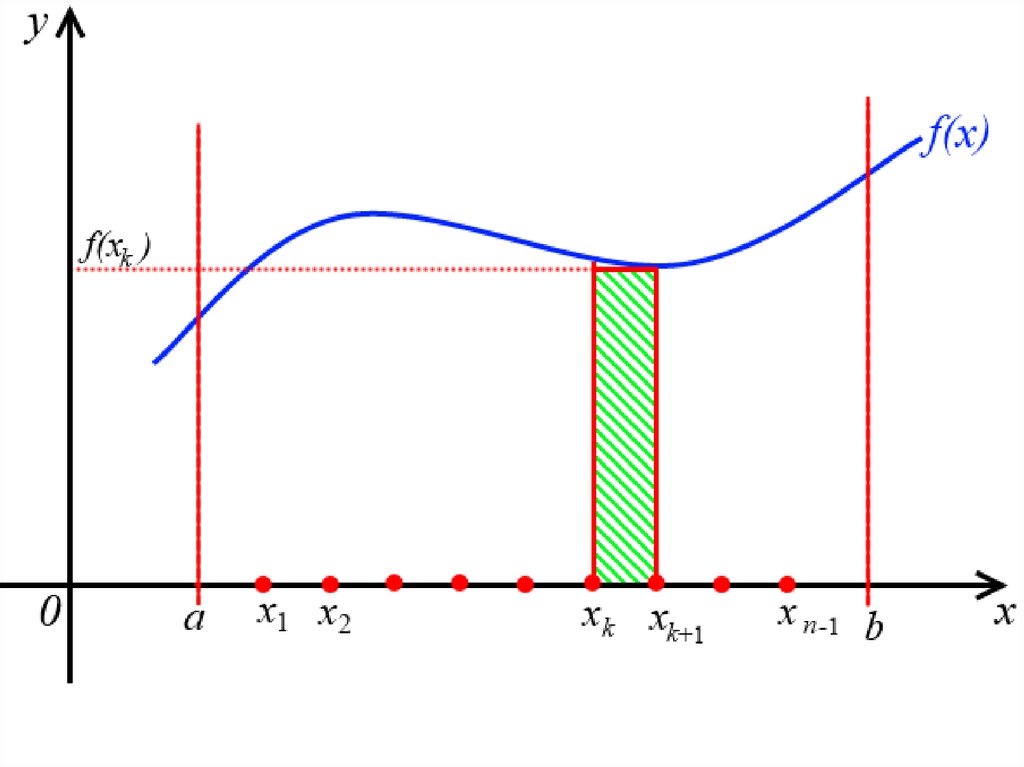
Рассмотрим отдельно одиниз столбиков – k−ый
столбик, то есть
криволинейную трапецию с
основанием
[ xk ; xk 1 ]
13.
Заменим его на прямоугольник стем же основанием, длина
которого равна
xk 1 xk xk
и высотой
f ( xk )
14.
15.
Sk16.
17.
18.
19.
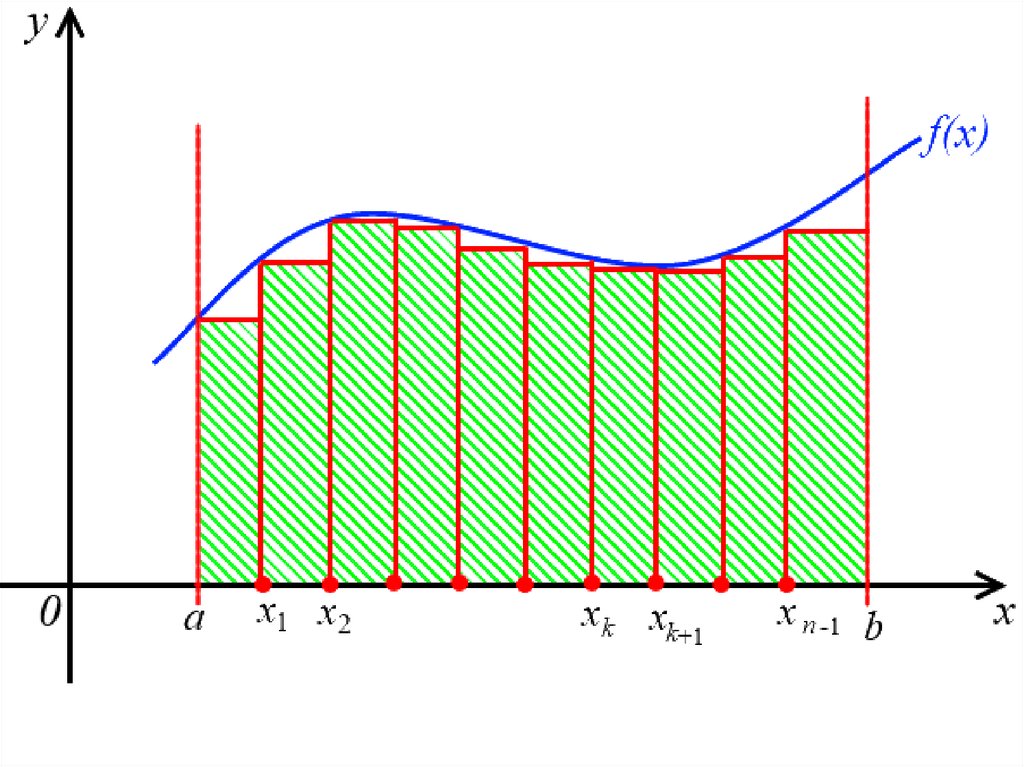
Sn f ( x0 ) x0 f ( x1 ) x1 f ( xn 1 ) xn 1S0 S1 Sk Sn 1
где x0 x1 x0
длина отрезка [ x0 ; x1 ]
20.
x1 x2 x1длина отрезка [ x1 ; x2 ] и т.д.
Выше было обговорено, что
отрезок [a; b] делится на
равные части, а это значит,
что
x0 x1 xn 1
21.
22.
23.
24.
25.
Опр. ПриращениеF(b)−F(a)
любой из первообразных F(x)
+ C при изменении аргумента
от x = a до x = b называется
определённым интегралом
от a до b
26.
27.
Числа a и b называютсяпределами интегрирования,
a−нижний предел, b−верхний
предел. Отрезок [a; b]
называется отрезком
интегрирования. Таким образом
по определению имеем
28.
bb
a
a
f
(
x
)
dx
F
(
x
)
F
(
b
)
F
(
a
)
|
b
| двойная подстановка.
a
29.
30.
Данная формула называетсяформулой Ньютона-Лейбница.
Данная формула
выражает связь между
определенными и
неопределенными
интегралами.
31.
32.
33.
34.
Теорема(Свойстваопределённого интеграла)
Пусть f(x) и g(x)
интегрируемы на [a,b]. Тогда
справедливы следующие
свойства определённого
интеграла
35.
36.
37.
38.
4. Определённый интегралот суммы(разности) равен
сумме(разности)
определённых интегралов
39.
40.
c [ a; b ]41.
СПАСИБО ЗАВНИМАНИЕ!




















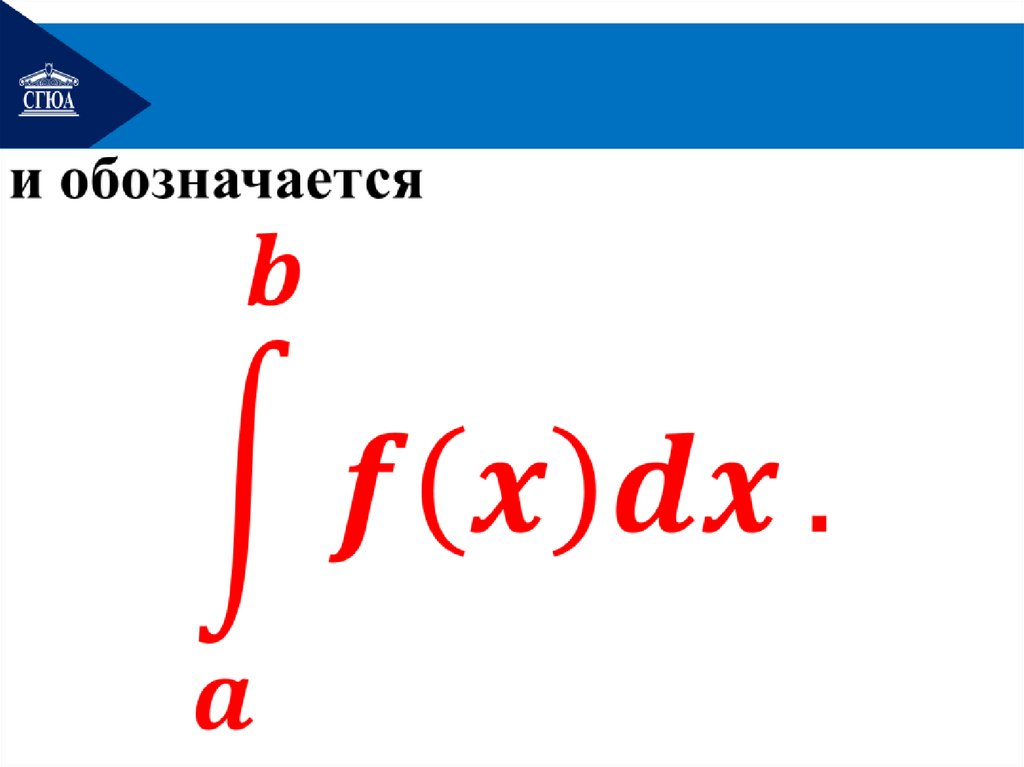











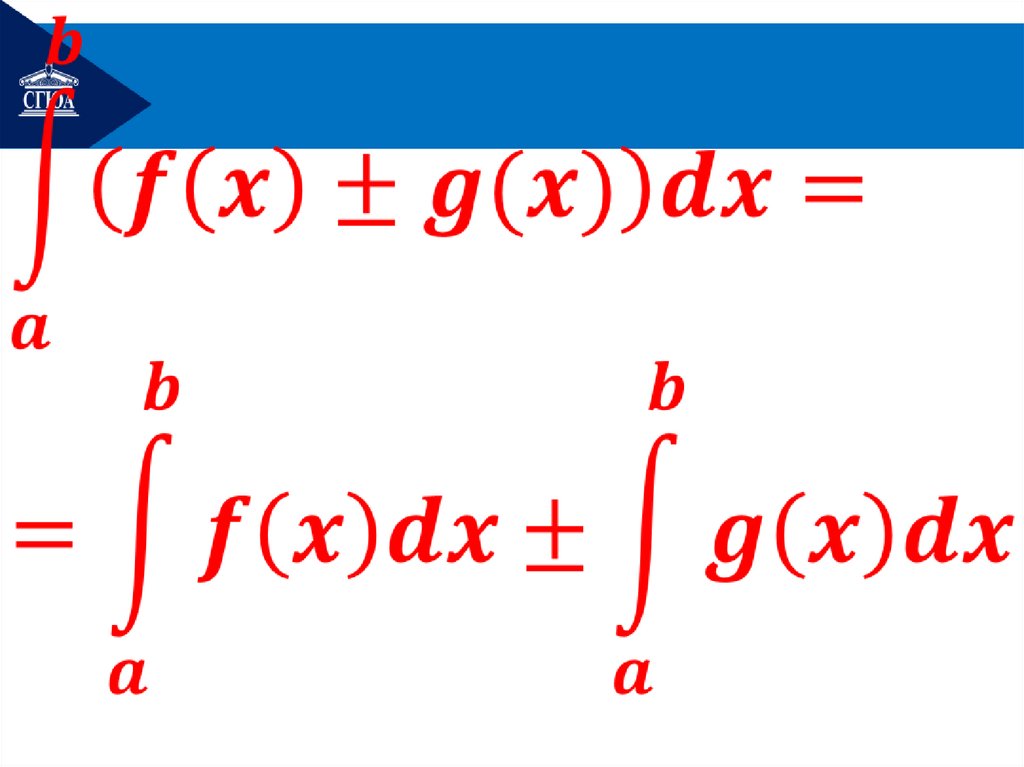


 mathematics
mathematics








