Similar presentations:
Решение систем двух уравнений, одно из которых линейное, а другое – второй степени
1.
Решение систем двухуравнений, одно из
которых линейное, а
другое – второй степени.
2.
Алгоритм решения системы двухуравнений с двумя
переменными методом подстановки:
1) из более простого уравнения системы выразить одно
неизвестное через другое;
2) подставить полученное выражение в другое уравнение вместо
выраженной переменной;
3) найти корень полученного уравнения с одним неизвестным;
4) подставить найденное значение в уравнение, полученное на
первом шаге, и найти вторую переменную;
5) записать ответ.
3.
Задание 1х + у = 3,
ቊ
ху = 10;
у = 3 − х,
ቊ
х ∙ 3 − х = −10;
3х – х2 = – 10
– х2 + 3х + 10 = 0
х2 – 3х – 10 = 0
х1 = 5
х2= – 2
у1 = 3 – 5 = – 2
Ответ: (5; – 2) (– 2; 5)
у2 = 3 – (– 2) = 5
4.
Задание 2х2 + у2 = 9,
ቊ
х + 2у = 3;
х = 3 − 2у,
ቊ
3 − 2у 2 + у2 = 9;
9 – 12у + 4у2 + у2 = 9
5у2 – 12у = 0
у(5у – 12) = 0
у1 = 0 у2 = 2,4
х1=3 – 2 0 = 3
х2 = 3 – 2 2,4 = 3 – 4,8 = – 1,8
Ответ: (3; 0); (– 1,8; 2,4)
5.
Задание 34х − у = 6,
ቊ 2
4х + у2 = 8;
у = 4х − 6,
ቊ 2
4х + 4х − 6 2 = 8.
4х2 + 16х2 – 48х + 36 – 8 = 0
20х2 – 48х + 28 = 0
5х2 – 12х + 7 = 0
Д = (– 12)2 – 4 5 7 = 144 – 140 = 4,
12+2
х1 =
= 1,4
10
у1 = 4 1,4 – 6 = – 0,4;
Ответ: (1,4; – 0,4), (1; – 2).
Д=2
12−2
х2 =
=1
10
у2 = 4 1 – 6 = – 2.
6.
Задание 4у = 3х − 4,
3х − у = 4,
ቊ 2
ቊ 2
х − 2ху = 3;
х − 2х(3х − 4) = 3.
х2 – 6х2 + 8х – 3 = 0
– 5х2 + 8х – 3 = 0
Д = 82 – 4 (– 5) (– 3) = 64 – 60 = 4,
−8+2
х1 =
= 0,6
−10
у1 = 3 0,6 – 4 = – 2,2;
Ответ: (0,6; - 2,2), (1; – 1).
−8−2
х2 =
=1
−10
Д=2
у2 = 3 1 – 4 = – 1.
7.
Задание 5х2 + ху = 8,
ቊ
2х + у = 6;
х2 + х 6 − 2х = 8,
ቊ
у = 6 − 2х.
х2 + 6х – 2х2 – 8 = 0
– х2 + 6х – 8 = 0
х2 – 6х + 8 = 0
х1 = 4
х2 = 2
у1 = 6 – 2 4 = – 2;
Ответ: (4; – 2), (2; 2).
у2 = 6 – 2 2 = 2.


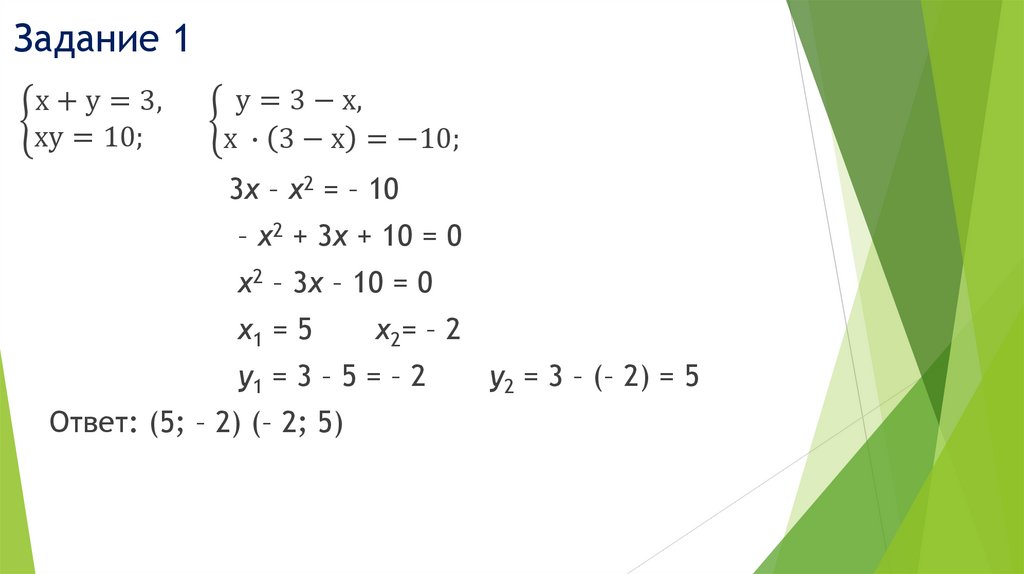


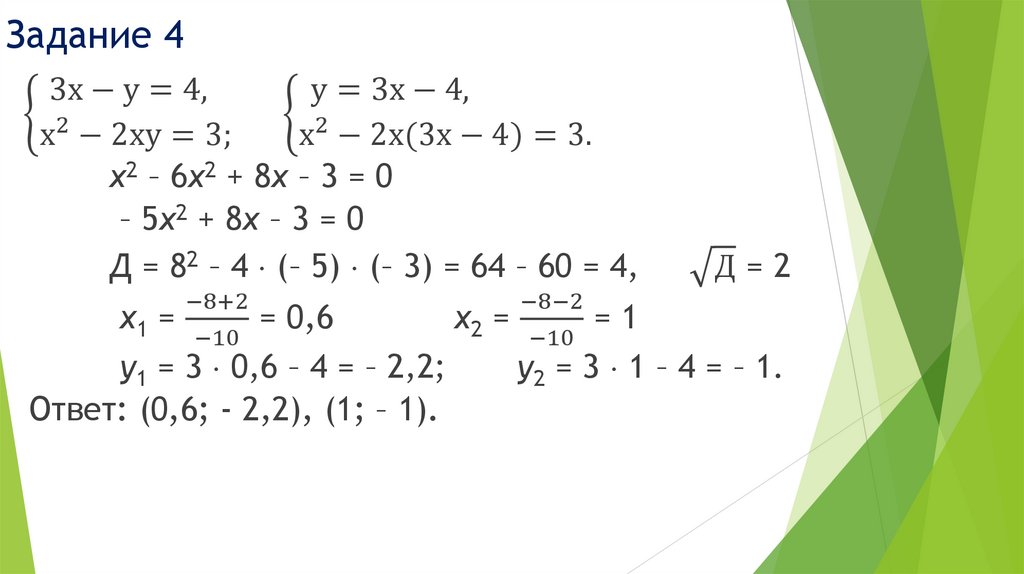
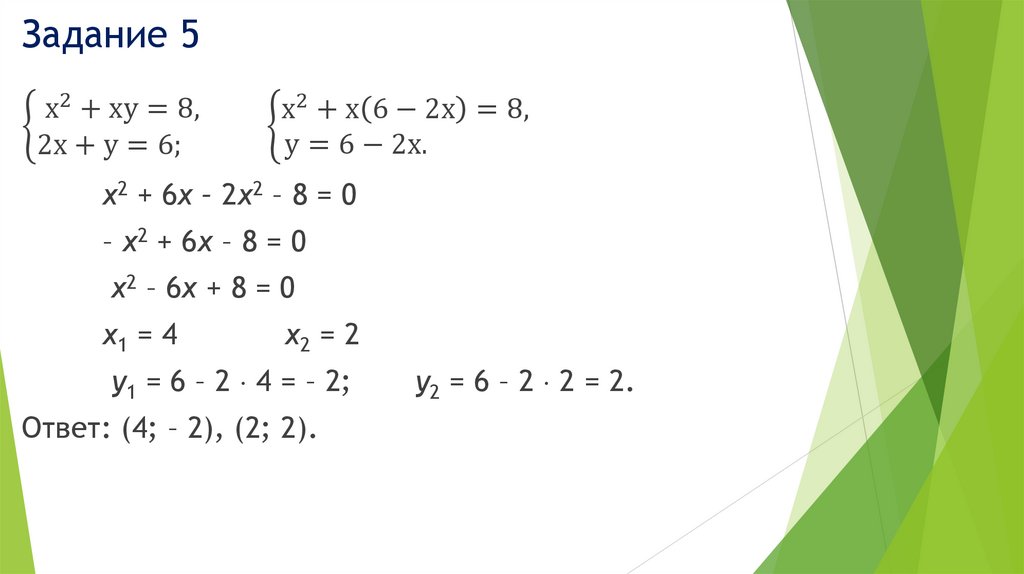
 mathematics
mathematics








