Similar presentations:
Квадратные уравнения. Урок изучения нового материала. 8 класс
1. Квадратные уравнения
КВАДРАТНЫЕ УРАВНЕНИЯУрок изучения нового материала.
8 класс
2. Если ты услышишь, что кто-то не любит математику, не верь. Её нельзя не любить - её можно только не знать.
3. Устный счёт
Решите уравнения:• X2
= 25
• X2
= 169
• X2
= 2,25
• X2
= -9
• X2
= 1,44
• X2
=3
• X2
=-4
• X2
= 17
4. Определение
Квадратным уравнением называется уравнениеах2 + bx + c = 0
где х – переменная;
а, b и с – действительные числа, причем а ≠ 0
a, b, с – коэффициенты квадратного уравнения
а - первый коэффициент
b - второй коэффициент
с - свободный член
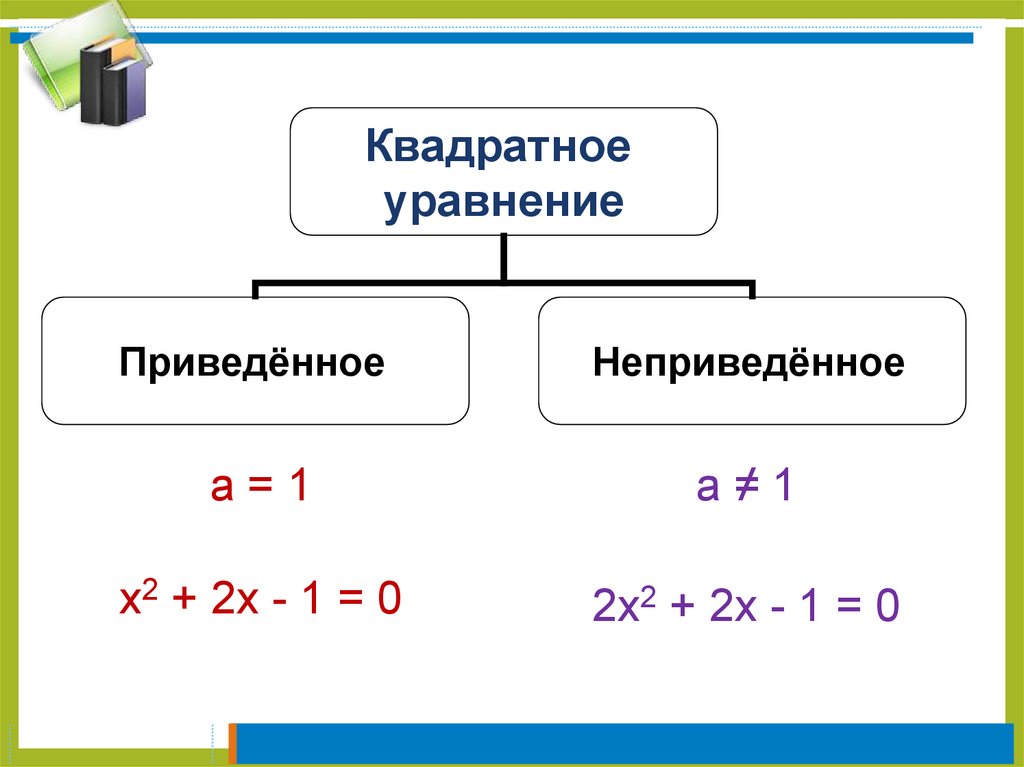
5.
Квадратноеуравнение
Приведённое
Неприведённое
а=1
а≠1
х2 + 2х - 1 = 0
2х2 + 2х - 1 = 0
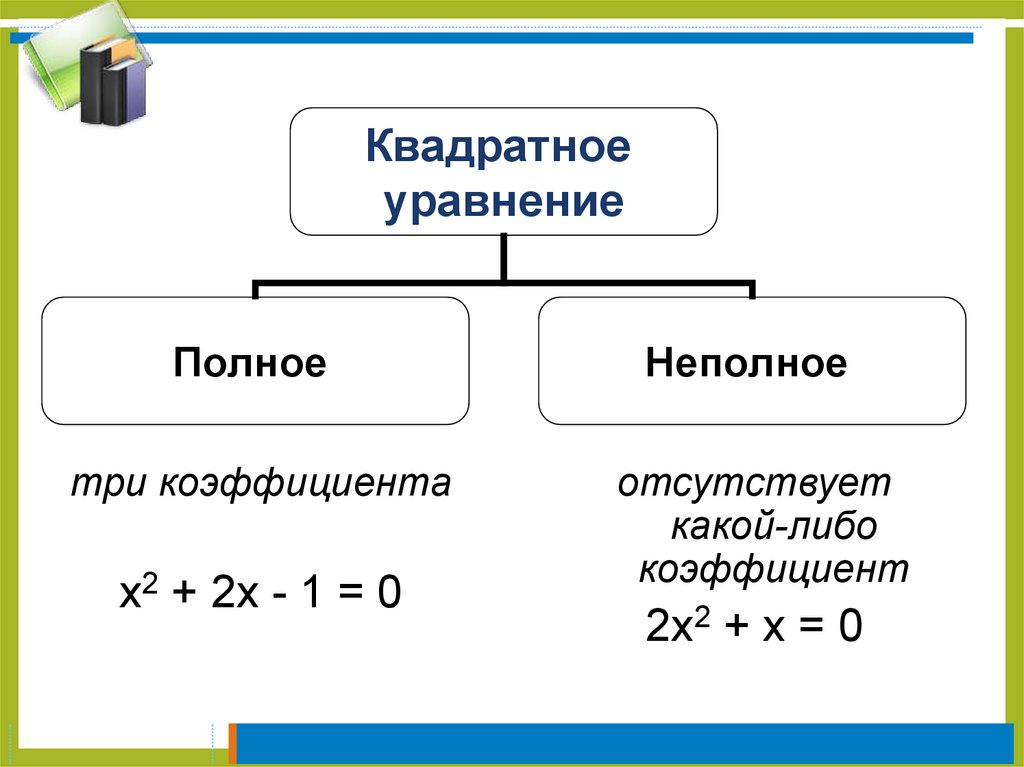
6.
Квадратноеуравнение
Полное
три коэффициента
х2 + 2х - 1 = 0
Неполное
отсутствует
какой-либо
коэффициент
2х2 + х = 0
7. Является ли уравнение квадратным?
а) 2,8х2 - 5х + 13 = 0б) 48х2 - 2х3 - 19 = 0
в) 2,3х2 + 2,6х - 0,16 = 0
г) 11 - 12х = 0
д) 27х2 - 15 = 0
е) -3х2 = 0
8. Определите коэффициенты квадратного уравнения:
• а)6х2 – х + 4 = 0
• б)
12х - х2 = 0
• в)
8 + 5х2 = 0
• г)
7х2 – х= 0
• д)
2х - 3х2 + 8= 0
• е)
25 + 16х2 = 0
9. Определение
Если в квадратном ах2 + bx + c=0 уравнениихотя бы один из коэффициентов b или с равен
0, то такое уравнение называется
неполным квадратным уравнением.
Виды:
• Если b = 0, то уравнение имеет вид
ах2 + c = 0
• Если с = 0, то уравнение имеет вид
ах2 + bx = 0
• Если b = 0 и с = 0, то уравнение имеет вид
ах2 = 0
10. Способы решения неполных квадратных уравнений ах2 + c = 0
Пример №1Пример №2
-3х2 +75=0
4х2 +8=0
-3х2 = -75
4х2 = -8
х2 = -75:(-3)
х2 = -8:4
х2 =25
х2 = -2
х1 = 5
х2 = -5
Ответ: х1 = 5
Ответ: корней нет
х2 = -5
11. Способы решения неполных квадратных уравнений
ах2 + bx =0ах2 =0
4х2 +12х = 0
0,2х2 =0
х (4х + 12) = 0
х2 =0 : 0,2
х = 0 или 4х + 12 = 0
х2 = 0
4х = - 12
х=0
х = -12 : 4
Ответ: х = 0
х = -3
Ответ: х1 = 0
х2 = -3
12. Самостоятельное решение примеров
а) 4х2 - 9 = 0б) -0,1х2 +10 = 0
в) 6а2 + 24 = 0
г) -5х2 + 6х = 0
д) 6а2 - 3а = 0
е) 2у + у2 =0
з) 10 - 3х2 = х2 + 10 – х
к) 1 - 2у + 3у2 = у2 - 2у + 1
13. Самопроверка решённых примеров
а) 4х2 – 9 = 0 б) -0,1х2 +10 = 04х2 = 9
-0,1х2 = -10
х2 = 9/4
х2 = -10:(-0,1)
х1 = 3/2
х2 = 100
х2 = -3/2
х1 = 10
х2 = -10
в) 6а2+ 24 = 0
6а2 = -24
а2 = -24:6
а2 = -4
корней нет
14. Самопроверка решённых примеров
г) -5х2 + 6х = 0х(-5х + 6) = 0
х = 0 или -5х + 6 = 0
-5х = -6
х = -6:(-5)
х = 1,2
Ответ:х1 =0; х2 =1,2
е) 2у + у2 =0
у(2+у) = 0
у = 0 или 2 + у = 0
у = -2
Ответ:у1 =0; у2 =1,2
д) 4а2 - 3а = 0
а(4а - 3) = 0
а = 0 или 4а - 3 = 0
4а = 3
а = 3/4
Ответ:х1 = 0; х2 = 3/4
15. Самопроверка решённых примеров
з) 10 - 3х2 = х2 + 10 - хк) 1-2у +3у2 = у2-2у+1
-3х2 - х2 - х =10 - 10
-2у +3у2 -у2+2у = 1-1
-4х2 - х = 0
2у2 = 0
-х(4х + 1) = 0
у2 = 0
-х = 0 или 4х + 1=0
у=0
х=0
4х = -1
х = -1/4
Ответ:х1 = 0; х2 = -1/4
Ответ: у = 0
16. Итог урока:
• Сформулируйте• Какое
определение квадратного уравнения.
уравнение называется неполным квадратным уравнением?
Приведите примеры.
• Сколько
корней может иметь неполное квадратное уравнение?
17. Рефлексия:
18. Домашнее задание
•Глава•№
4, п. 24
24.9, 24.10, 24.11 (в, г)
















 mathematics
mathematics