Similar presentations:
Теория вероятностей. Случайные величины
1. Лекция № 5 Теория вероятностей
Случайные величины2.
Опр. Случайной называетсявеличина, которая в результате
опыта может принять одно и
только одно возможное
значение, неизвестно заранее,
какое именно.
Сокращенно – СВ.
3.
Например, посеяно 100 зеренпшеницы для определения ее
всхожести. Число взошедших
зерен есть СВ, которая может
принять одно из значений: 0, 1,
2, …, 100.
4.
Еще примеры СВ:• число очков, выпавших при бросании
игральной кости;
• число выстрелов до первого попадания в
цель;
• время безотказной работы прибора;
• рост человека;
• курс доллара;
• количество бракованных деталей в партии;
• температура воздуха;
• выигрыш игрока;
• координата точки при случайном выборе ее
на [0; 1];
• прибыль фирмы, и т.п.
5.
Случайныеобозначают
латинскими
(или строчными
буквами ξ (кси), η
θ (тэта), ψ (пси) и
т.д.) , а
принимаемые ими
значения
соответственно
6.
Опр. СВназывается
дискретной, если
она принимает
отдельные,
изолированные
друг от друга
возможные
значения,
которые можно
7.
Опр. Непрерывнойслучайной
величиной
называется такая
СВ, возможные
значения которой
непрерывно
заполняют какойто промежуток,
конечный или
8.
Опр. Закономраспределения СВ
называется
соотношение
(правило, таблица,
функция, график),
устанавливающее
связь между
возможными
значениями СВ и
9.
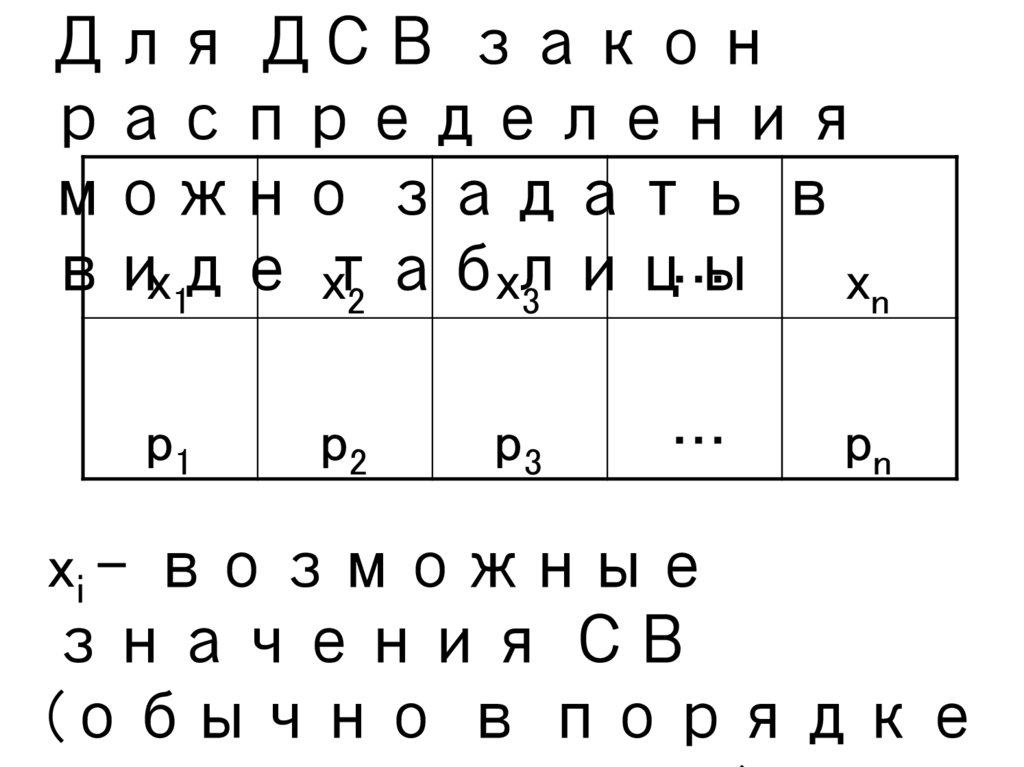
Для ДСВ законраспределения
можно задать в
виде
таблицы
x1
x2
x3
…
xn
p1
p2
p3
…
pn
xi – возможные
значения СВ
(обычно в порядке
10.
Такую таблицуназывают рядом
распределения.
Т.к. события {X = x1}, {X =
x2}, ... несовместны и
образуют полную
группу, то сумма
их вероятностей
pi 1
равна единице
,
т.е.
i
11.
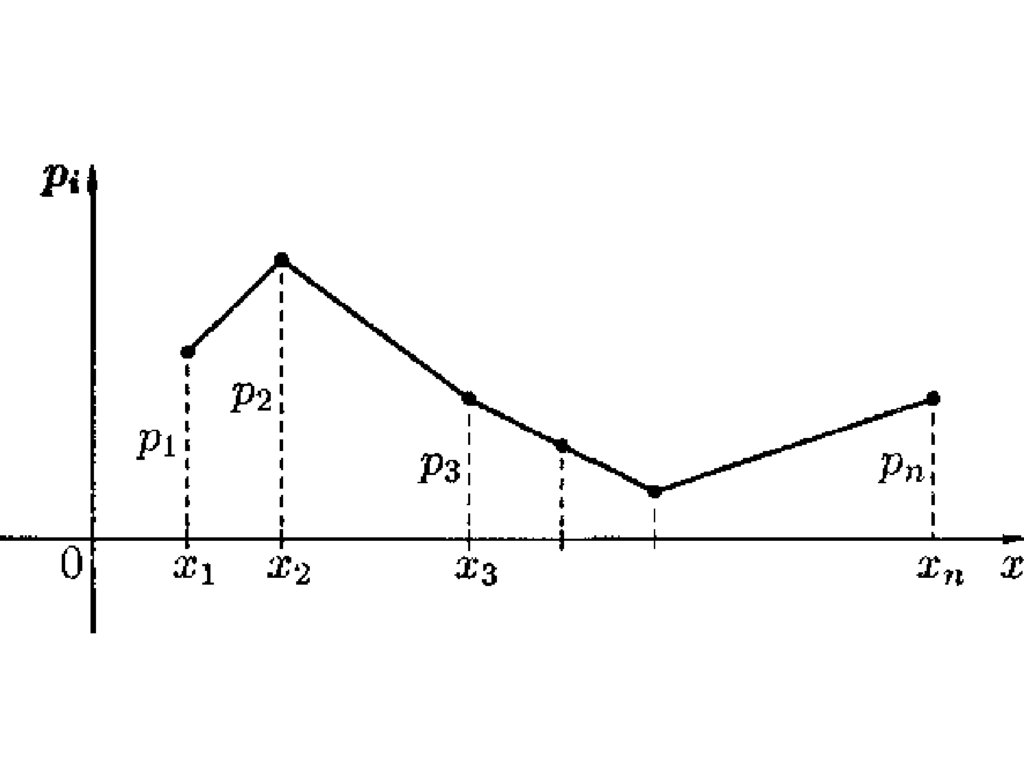
Законраспределения
ДСВ можно задать
графически, если
на оси абсцисс
отложить
значения СВ, а на
оси ординат —
вероятности этих
значений.
Ломаную,
12.
13. Пример
В урне 8 шаров, изкоторых 5 белых,
остальные —
черные. Из нее
вынимают наудачу
3 шара. Найти
закон
14. Решение
Возможныезначения СВ
X — числа белых
шаров в выборке
равны
x1 = 0, x2 = 1, x3 = 2, x4 = 3.
15.
C C1
p1 P{ X 0}
3
C8
56
0
5
3
3
C C
15
p2 P{ X 1}
3
C8
56
1
5
2
3
16.
C C30
p3 P{ X 2}
3
C8
56
2
5
1
3
C C
10
p4 P{ X 3}
3
C8
56
3
5
0
3
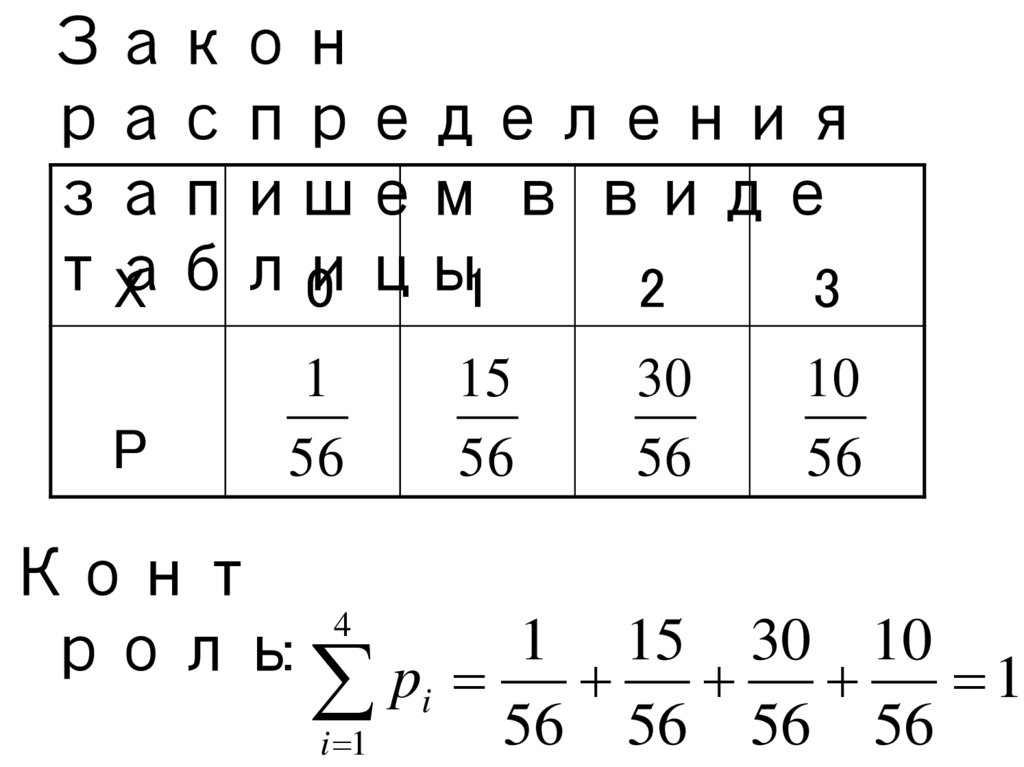
17.
Законраспределения
запишем в виде
таблицы
X
0
1
2
3
P
1
56
15
56
30
56
10
56
Конт
4
1 15 30 10
роль:
pi
1
56 56 56 56
i 1
18. Интегральная функция распределения (функция распределения)
Интегральнаяфункция
распределения
(функция
распределения
)
19.
Универсальнымспособом задания
закона
распределения
вероятностей,
пригодным как
для ДСВ, так и для
НСВ, является
функция
20.
Опр.Интегральной
функцией
распределения
СВ X называется
функция F(x),
выражающая
F ( x) P( X x).
вероятность
того, что СВ X
примет значение,
21. Свойства интегральной функции F(x).
1. Значенияинтегральной
функции
принадлежат
отрезку [0; 1].
22.
2. F(x) - неубывающаяфункция, т.е. F(x2) ≥ F(x1),
если x2 > x1.
lim F ( x) 0,
3. x
lim F ( x) 1.
x
23.
4. Вероятностьтого, что СВ X
примет значение
в интервале (a; b),
равна приращению
интегральной
функции на этом
интервале:
P(a < X < b) = F(b) – F(a).
24.
5. Вероятностьтого, что НСВ X
примет одно
конкретное
значение, равна
нулю,
т.е. P(x = x0) = 0.
⇒ для НСВ
25. Пример.
По условиюпредыдущего
примера найти
функцию
распределения F(x)
и построить ее
график.
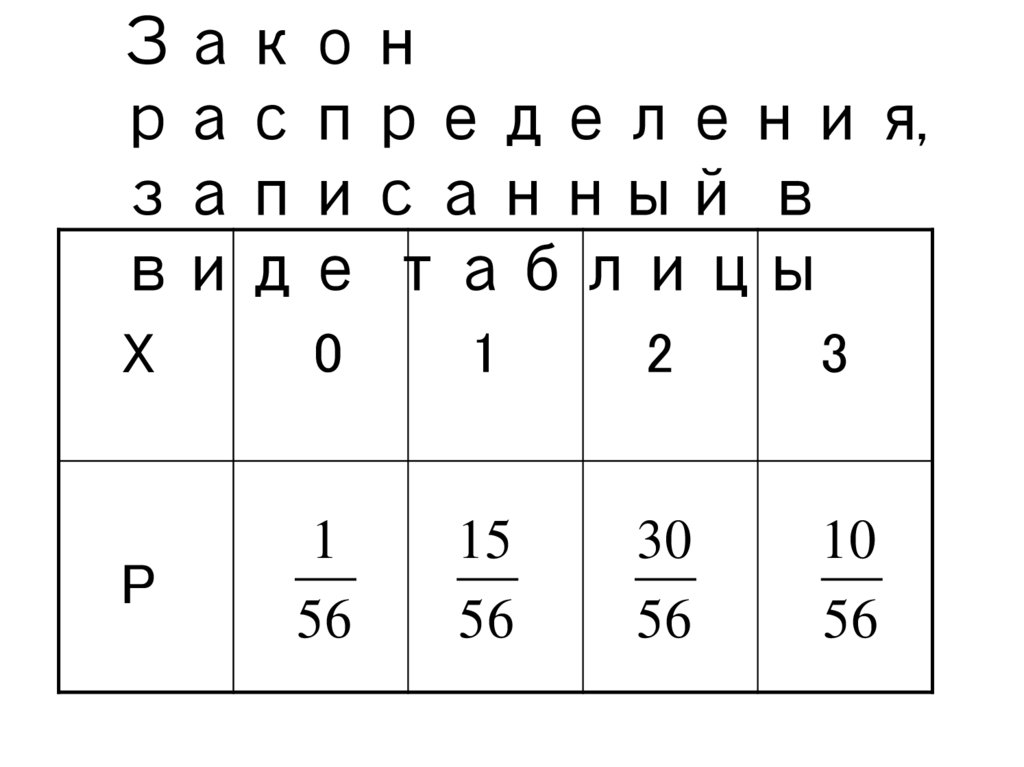
26.
Законраспределения,
записанный в
виде таблицы
X
0
1
2
3
P
1
56
15
56
30
56
10
56
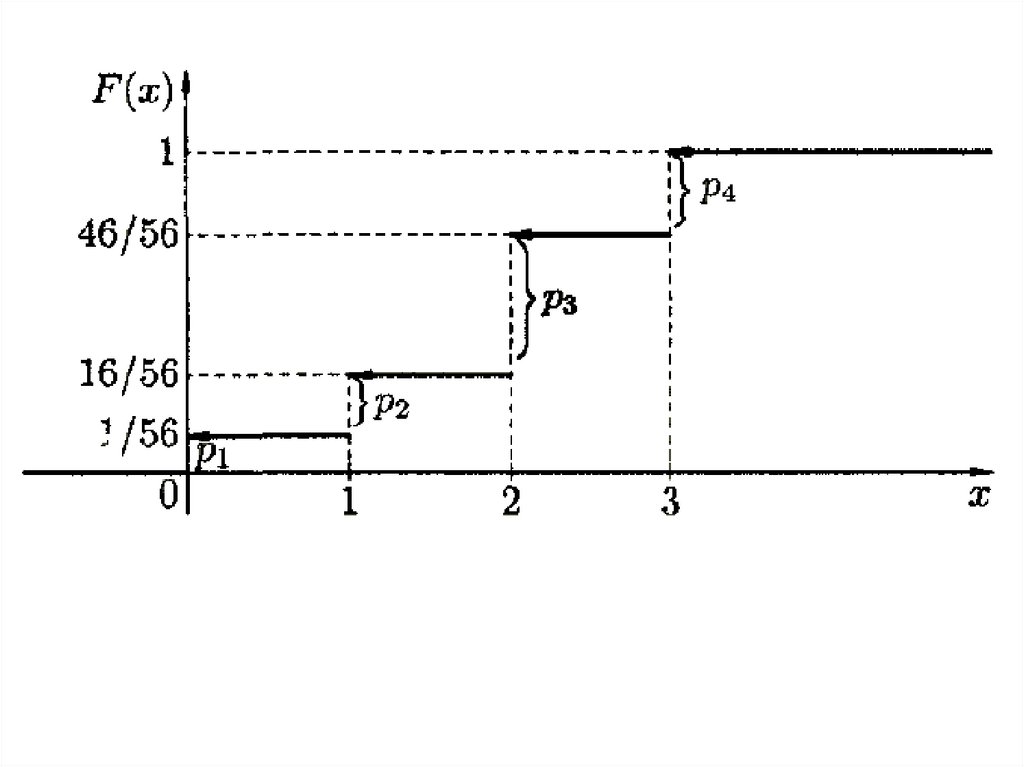
27.
Решение.Будем задавать
различные
значения х и
находить для них
F(x) = P(X < x):
28.
• 1. Если х ≤ 0, то,очевидно,
F(x) = P(X
< 0) = 0;
• 2. Если 0 < х ≤ 1, то
F(x) = P(X < x) = P(X = 0) = 1/56;
• 3. Если 1 < х ≤ 2, то
F(x) = P(X = 0) + P(X = 1) = 1/56 +
29.
• 4. Если 2 < х ≤ 3, тоF(x) = P(X = 0) + P(X = 1) +
P(X = 2) = 1/56 + 15/56 + 30/56 =
46/56.
• 5. Если 3 < х, то
F(x) = P(X = 0) + P(X = 1) +
P (X
= 2) + P(X = 3) = 46/56 + 10/56 = 1.
30.
0,1 / 56,
F ( x) 16 / 56,
46 / 56,
1,
если
x 0;
если 0 x 1;
если 1 x 2;
если 2 x 3;
если
3 x.
31.
32. Дифференциальная функция распределения (плотность распределения)
Дифференциальная
функция
распределен
ия
(плотность
распределен
ия)
33.
Важнейшейхарактеристико
й НСВ (помимо
функции
распределения)
является
плотность
распределения
вероятностей.
34.
Опр. Плотностьюраспределения
вероятностей
(плотностью
распределения,
плотностью
вероятностей или
просто
плотностью) НСВ X
называется
35.
Интегральнаяфункция
выражается через
дифференциальну
x :
ю формулой
F ( x) f (t )dt
36. Свойства дифференциальной функции распределения
Свойствадифференциаль
ной функции
распределения
• 1. f (x) ≥ 0, т.е.
дифференциальна
я функция
неотрицательна.
37.
• 2. Вероятностьтого, что СВ
примет значение,
принадлежащее
интервалу
(-∞; ∞),
равна
единице:
f
(
x
)
d
x
1
38.
• 3. Вероятностьтого, что НСВ X
примет значение
в интервале (a; b),
равна
определенному
интегралу от
b
дифференциально
P(a X b) f ( x)dx
й функции
распределения
,
a
39.
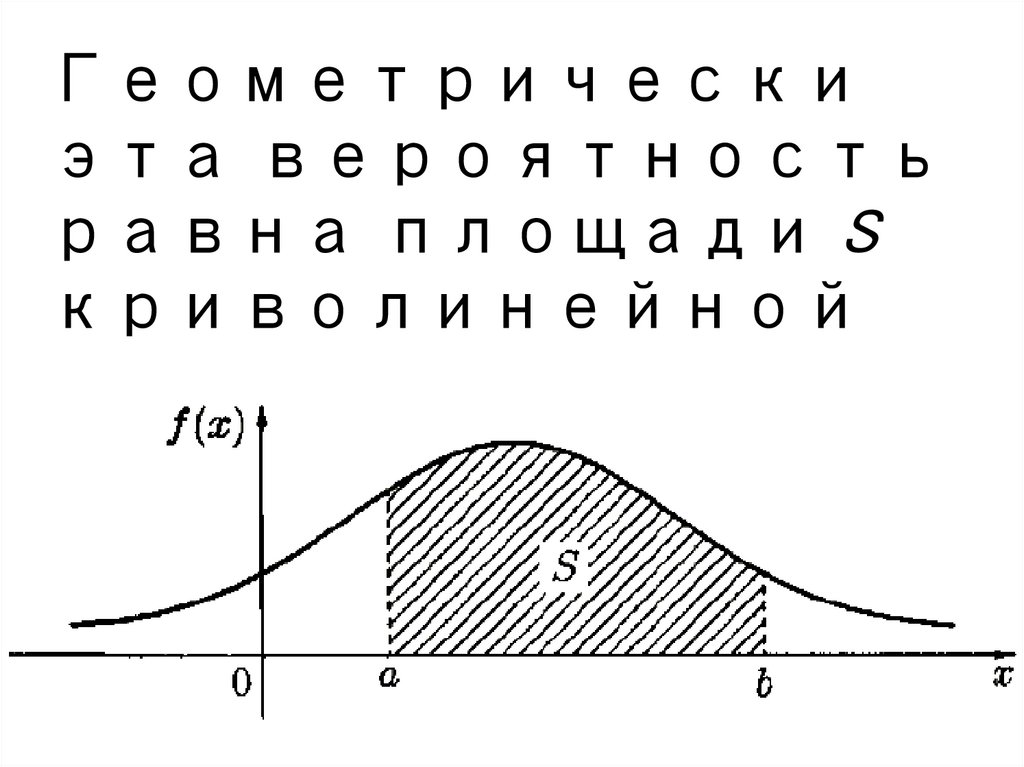
Геометрическиэта вероятность
равна площади S
криволинейной
трапеции:












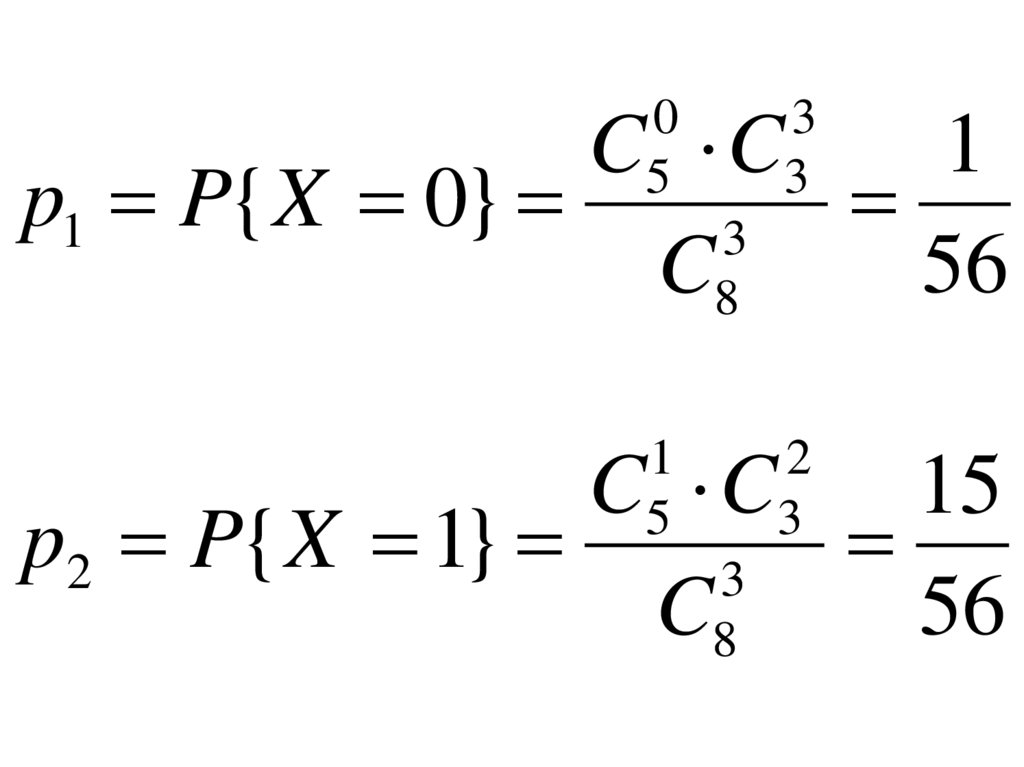
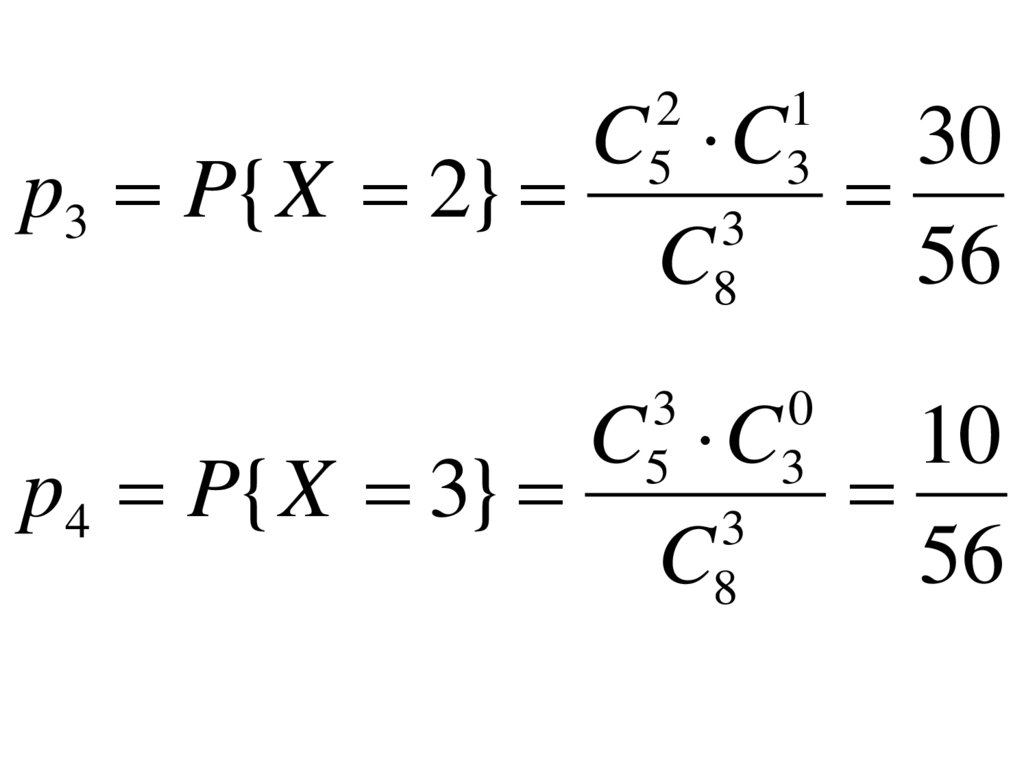




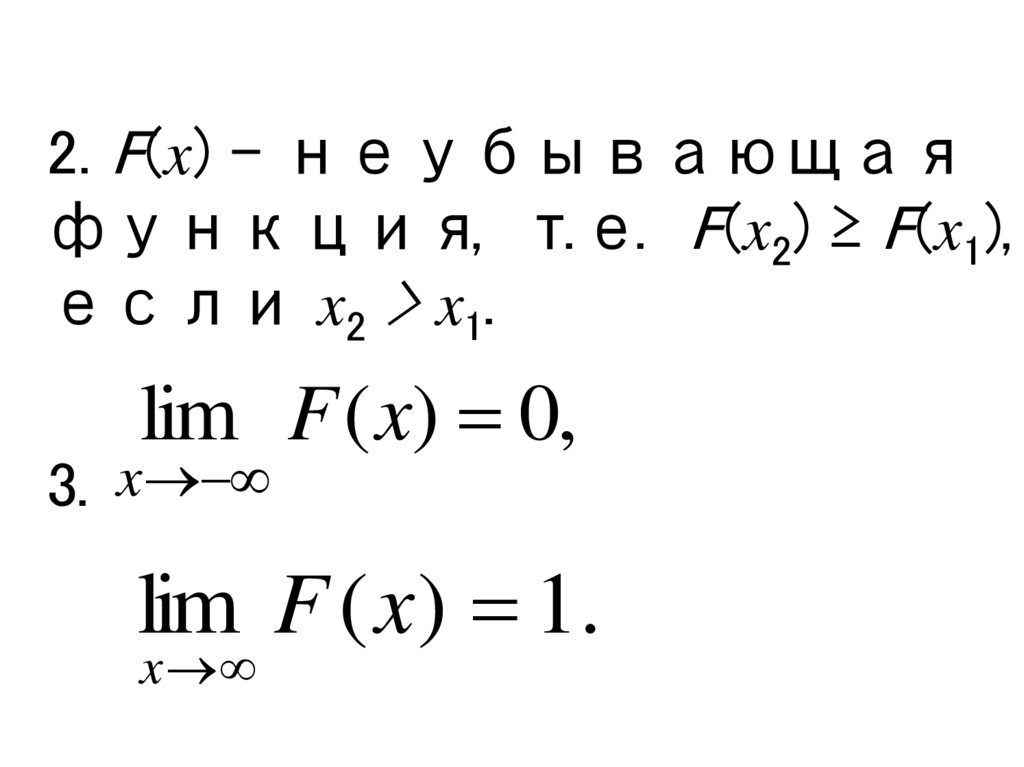




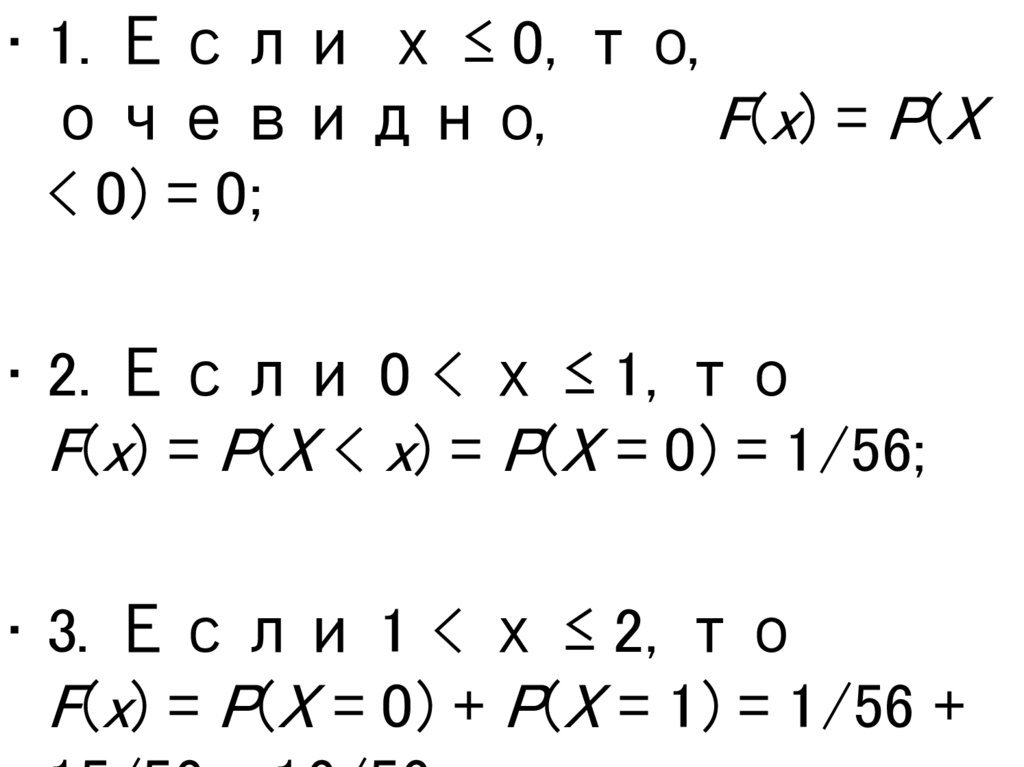
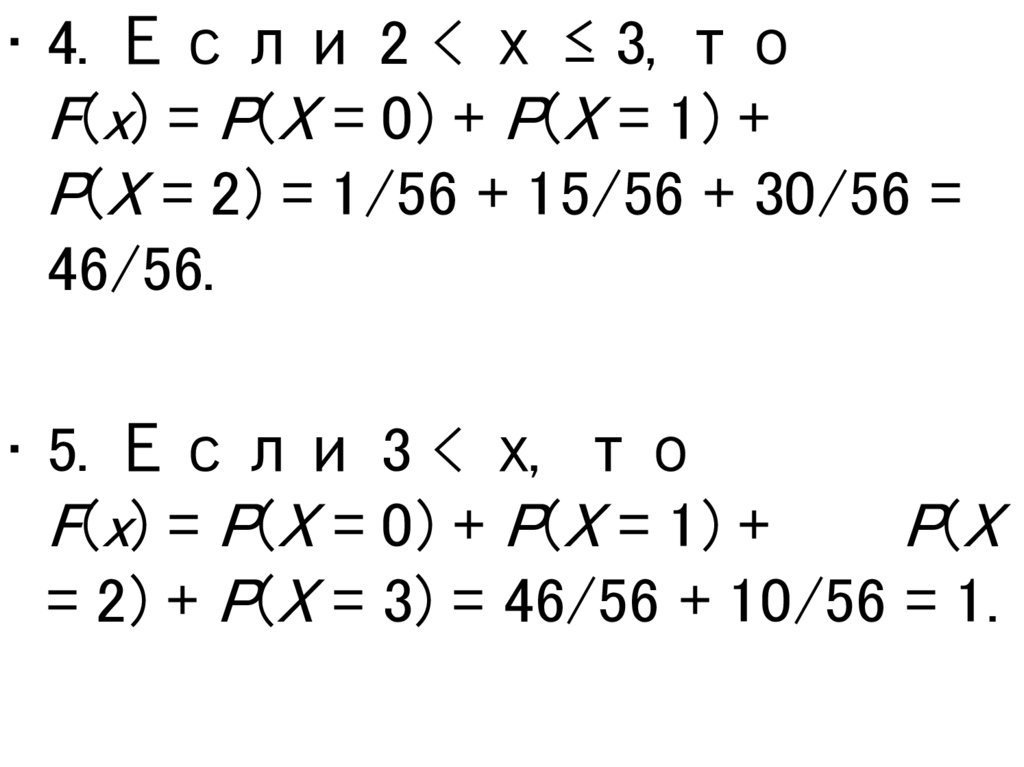
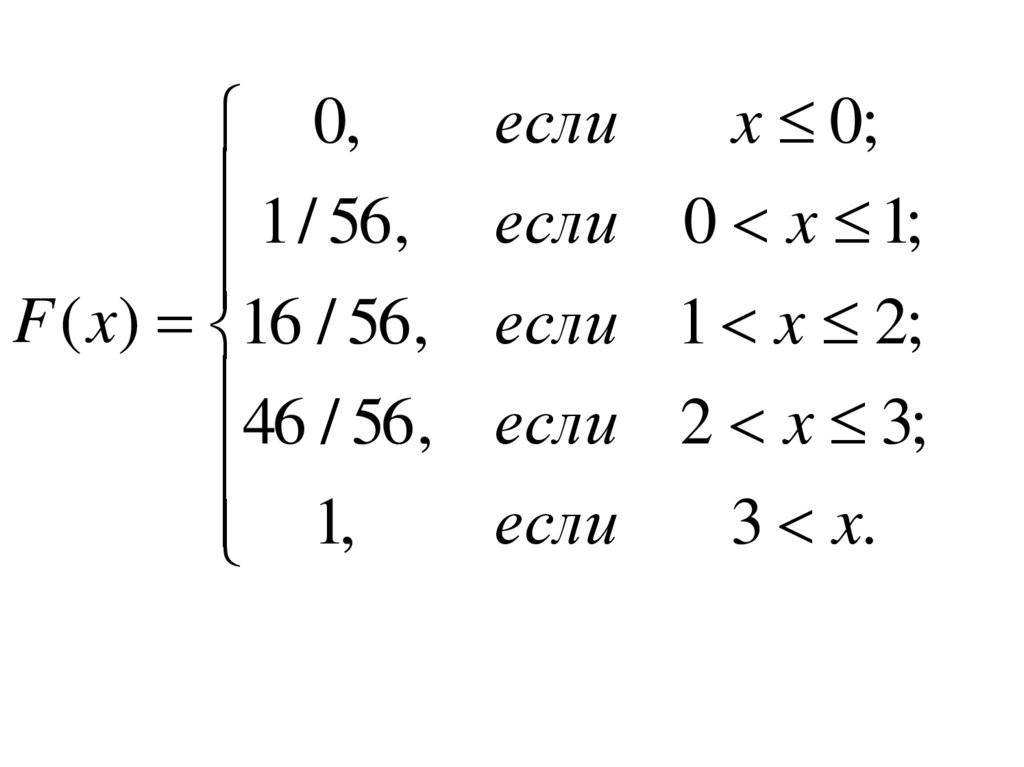



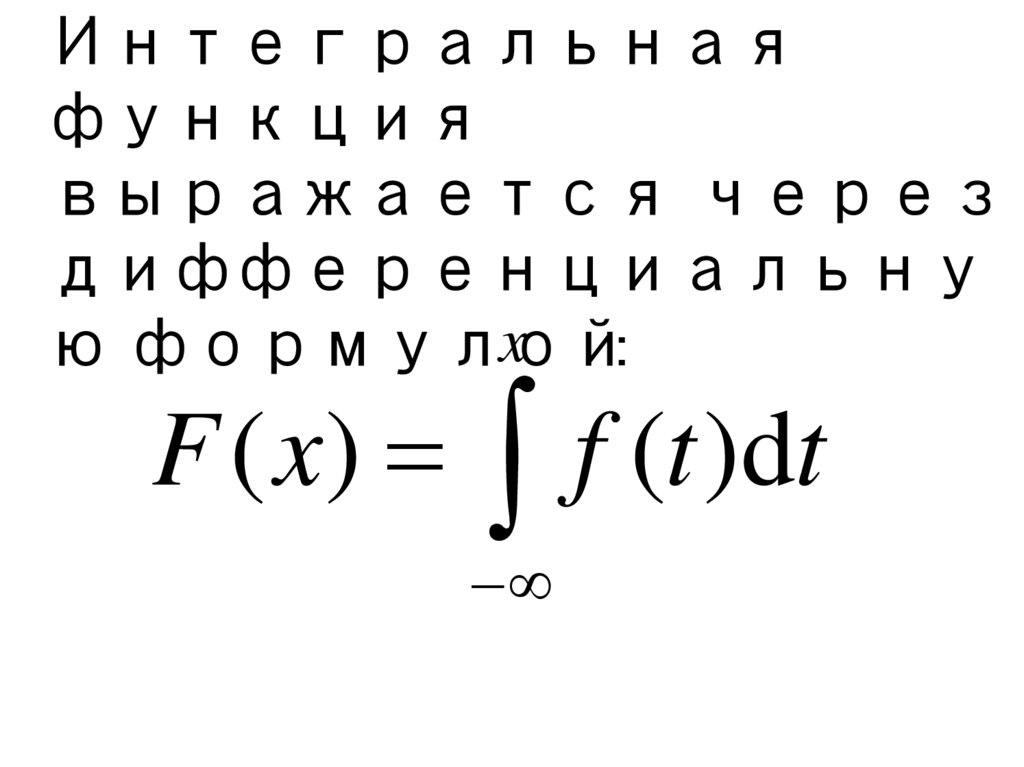



 mathematics
mathematics








