Similar presentations:
Усечённый конус
1. Усеченный конус
2.
3.
4.
5.
6.
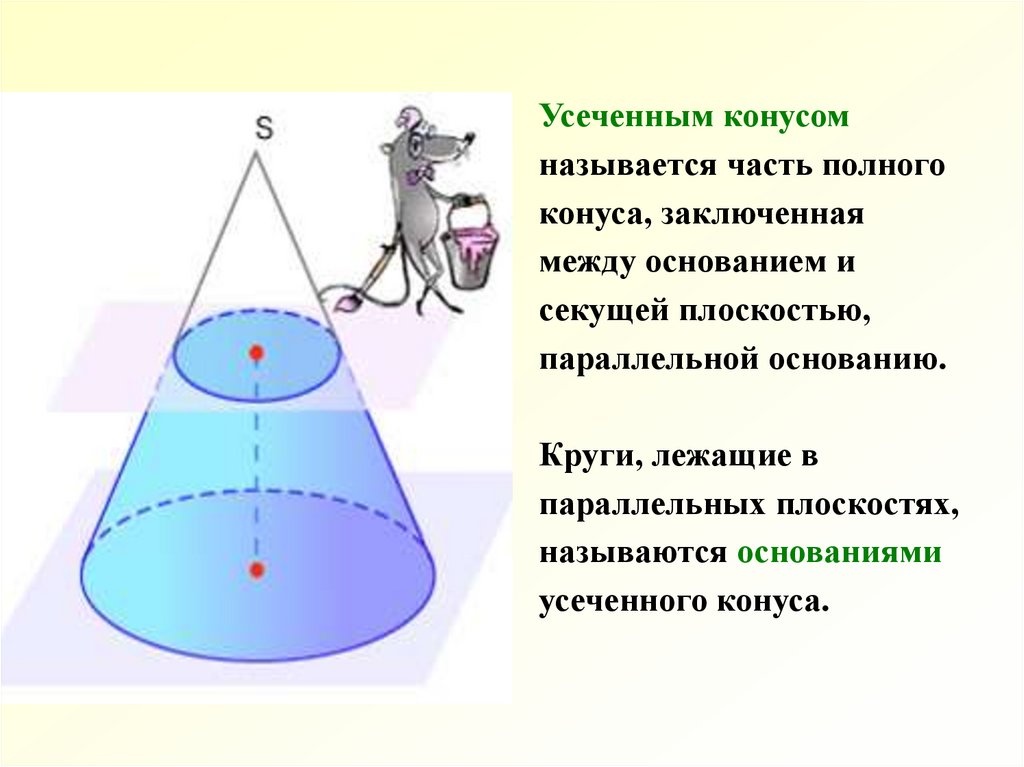
Усеченным конусомназывается часть полного
конуса, заключенная
между основанием и
секущей плоскостью,
параллельной основанию.
Круги, лежащие в
параллельных плоскостях,
называются основаниями
усеченного конуса.
7.
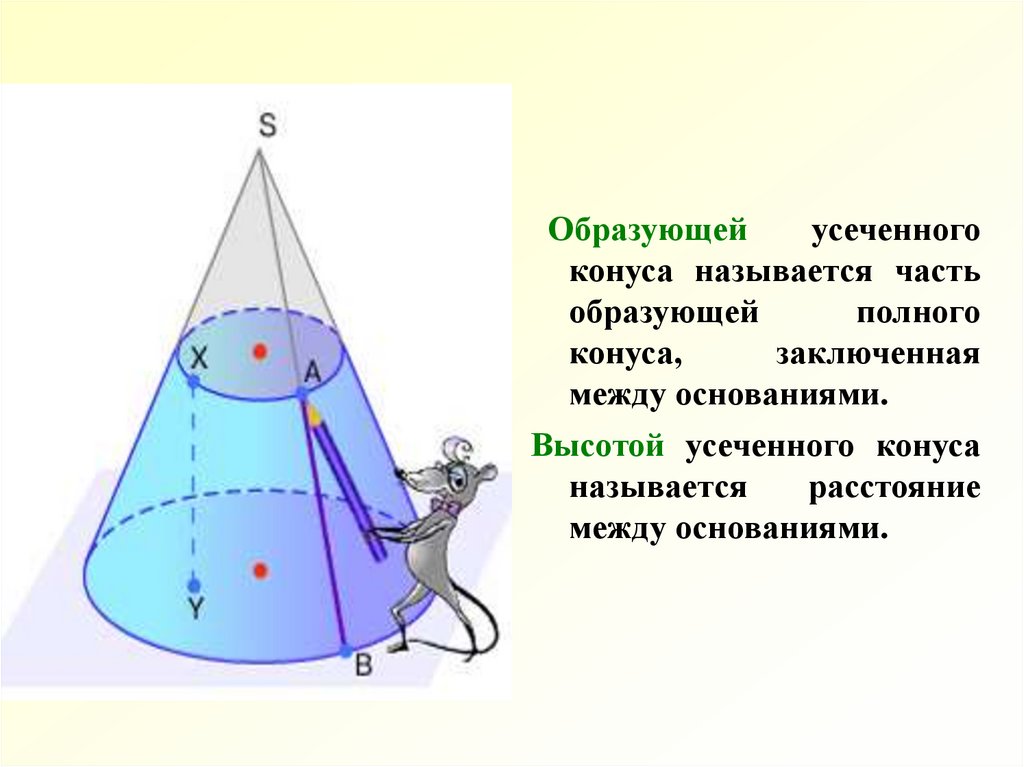
Образующейусеченного
конуса называется часть
образующей
полного
конуса,
заключенная
между основаниями.
Высотой усеченного конуса
называется
расстояние
между основаниями.
8.
Пусть в конусе,высота которого
известна,
проведено сечение,
находящееся
на
расстоянии три от
вершины.
Чему
равна образующая
получившегося
усеченного конуса,
если
известна
образующая
полного конуса?
?
8
9.
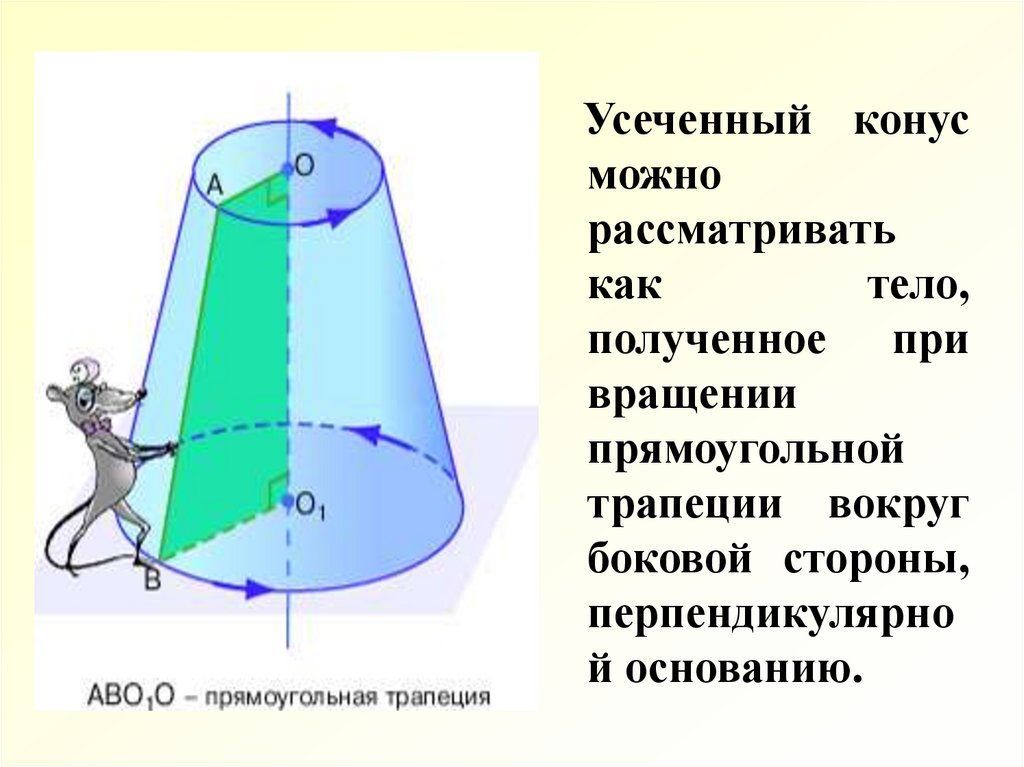
Усеченный конусможно
рассматривать
как
тело,
полученное при
вращении
прямоугольной
трапеции вокруг
боковой стороны,
перпендикулярно
й основанию.
10.
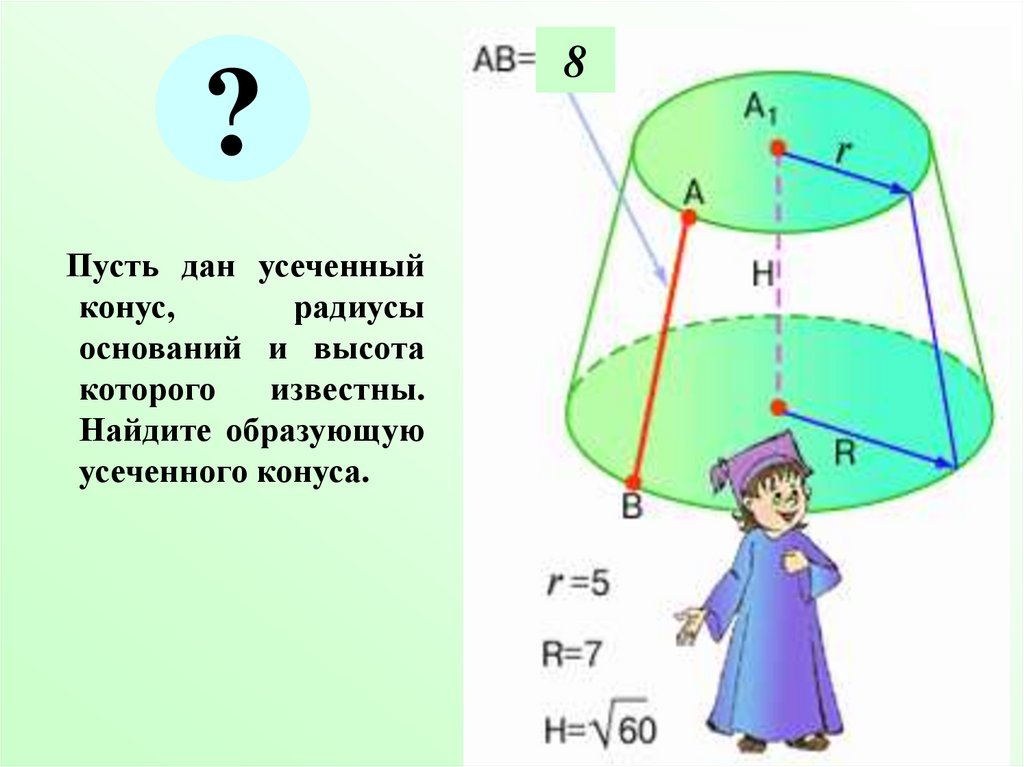
?Пусть дан усеченный
конус,
радиусы
оснований и высота
которого
известны.
Найдите образующую
усеченного конуса.
8
11.
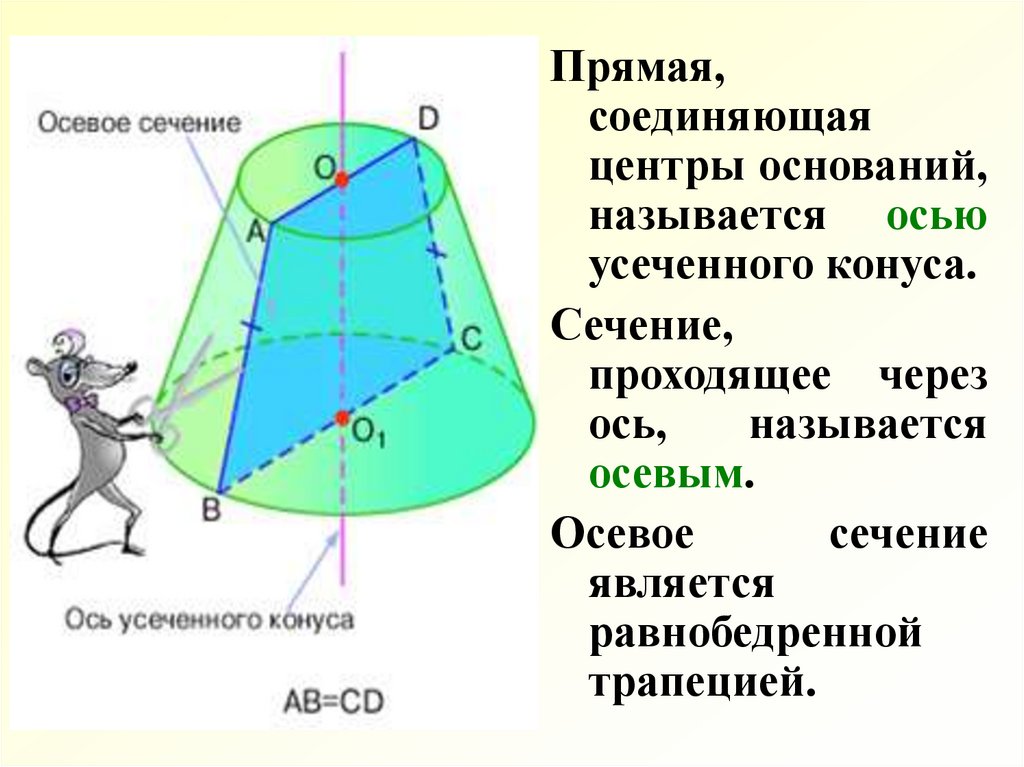
Прямая,соединяющая
центры оснований,
называется осью
усеченного конуса.
Сечение,
проходящее через
ось,
называется
осевым.
Осевое
сечение
является
равнобедренной
трапецией.
12.
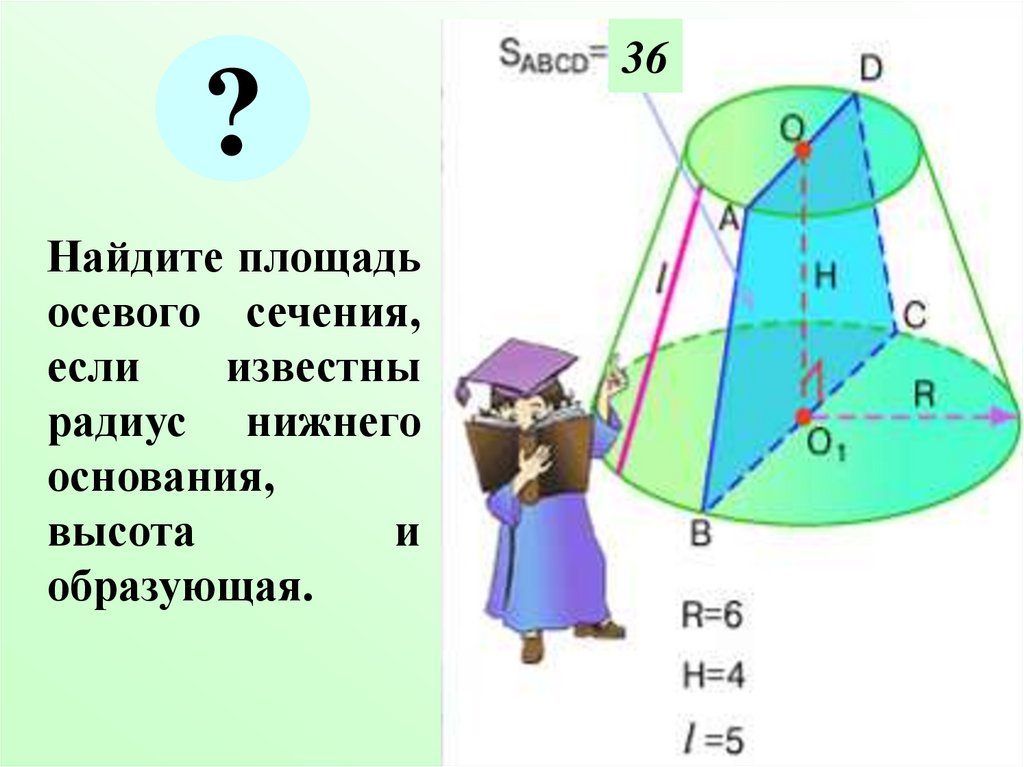
?Найдите площадь
осевого сечения,
если
известны
радиус нижнего
основания,
высота
и
образующая.
36
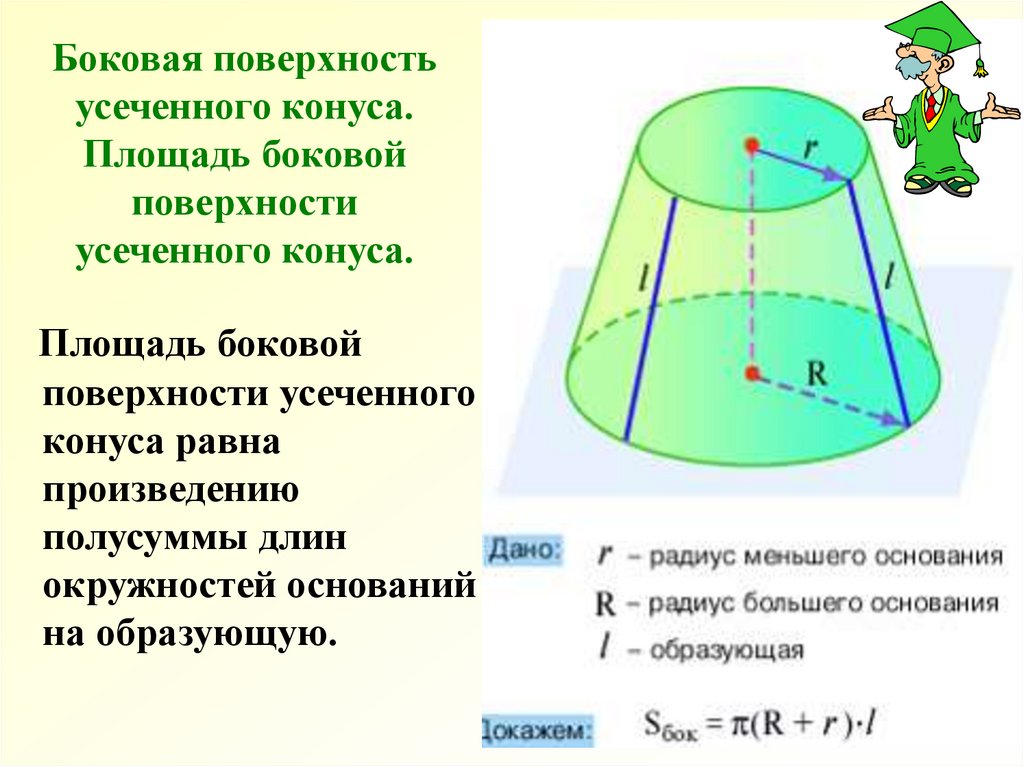
13. Боковая поверхность усеченного конуса. Площадь боковой поверхности усеченного конуса.
Площадь боковойповерхности усеченного
конуса равна
произведению
полусуммы длин
окружностей оснований
на образующую.
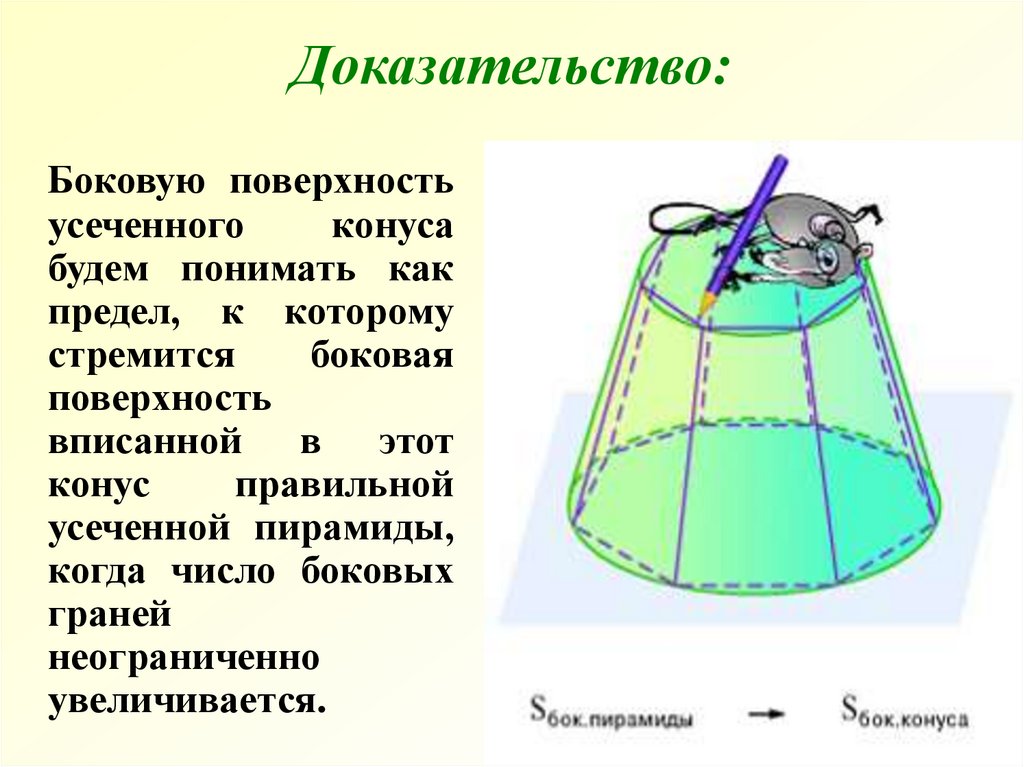
14. Доказательство:
Боковую поверхностьусеченного
конуса
будем понимать как
предел, к которому
стремится
боковая
поверхность
вписанной в этот
конус
правильной
усеченной пирамиды,
когда число боковых
граней
неограниченно
увеличивается.
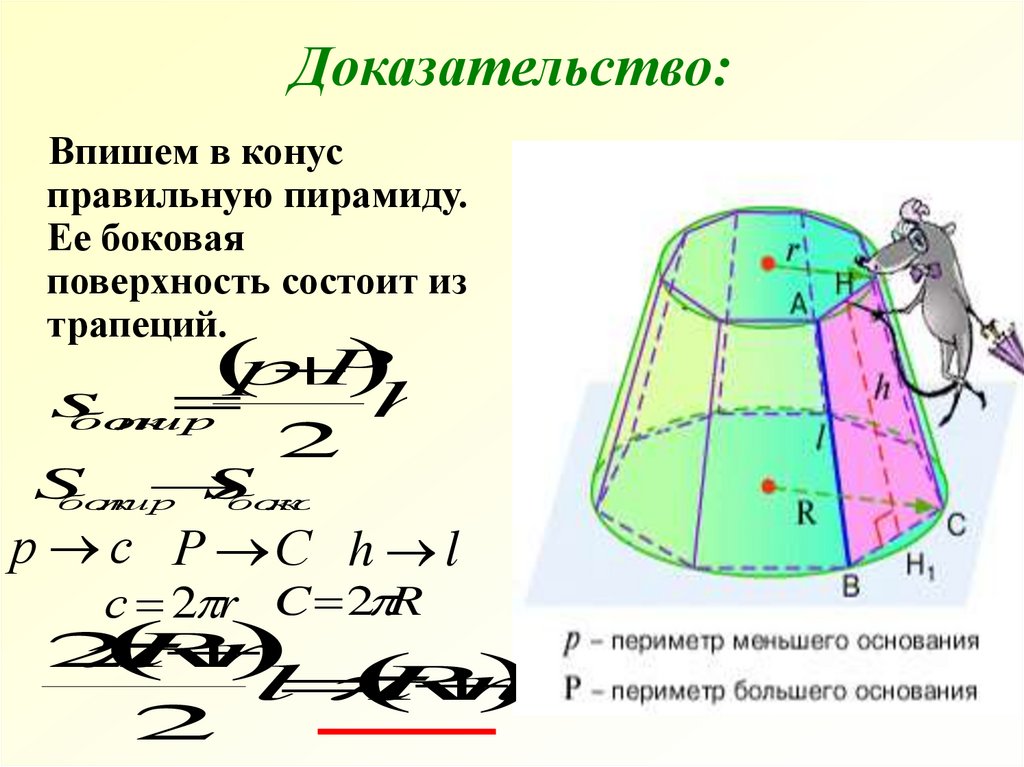
15. Доказательство:
Впишем в конусправильную пирамиду.
Ее боковая
поверхность состоит из
трапеций.
р
Р
h
s
бок
.пир
2
S
S
бок
.пир
бок
.кон
р с Р С h l
с 2 r C 2 R
2
R
r
l
R
r
l
2
16.
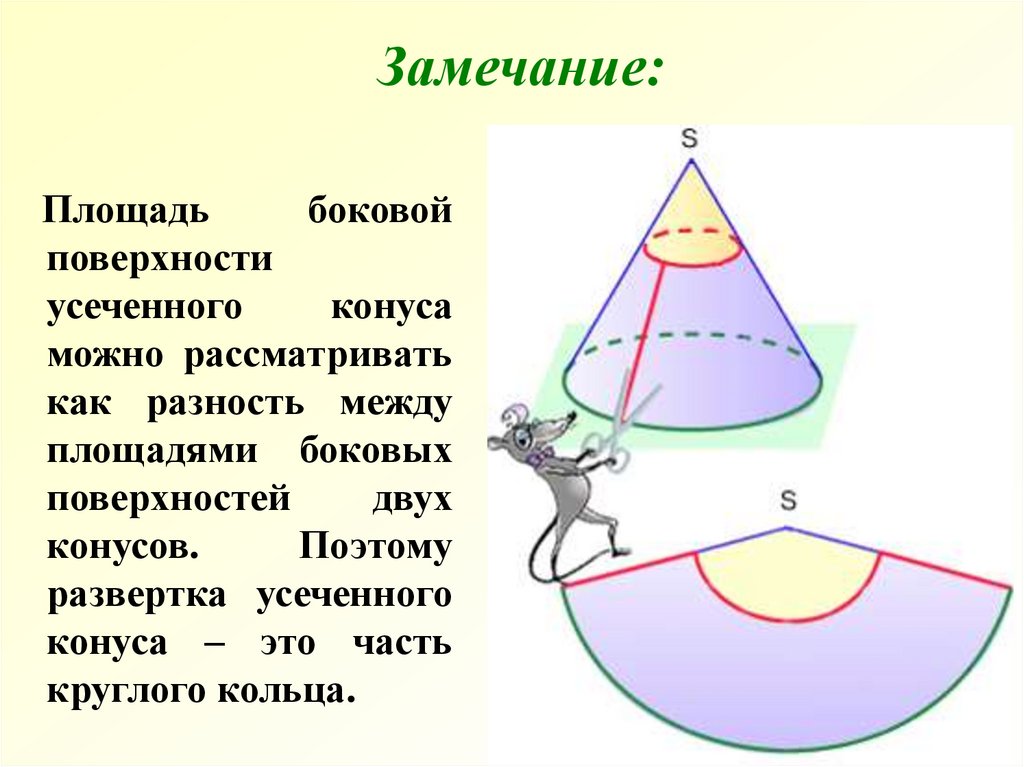
Замечание:Площадь
боковой
поверхности
усеченного
конуса
можно рассматривать
как разность между
площадями боковых
поверхностей
двух
конусов.
Поэтому
развертка усеченного
конуса – это часть
круглого кольца.
17.
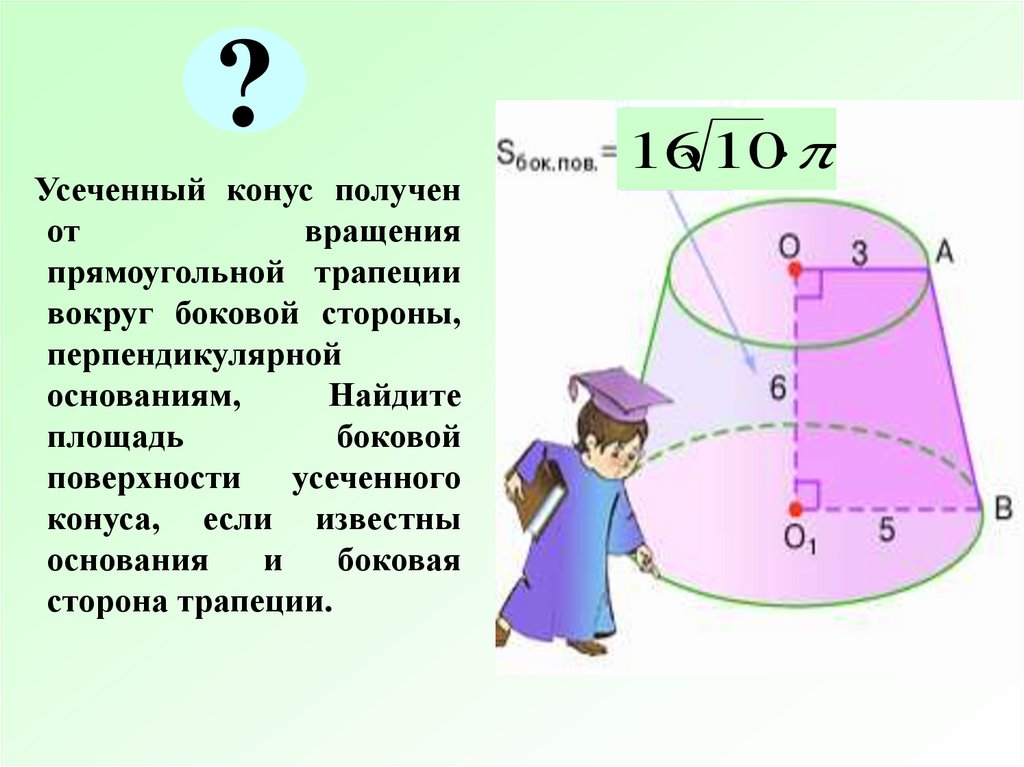
?Усеченный конус получен
от
вращения
прямоугольной трапеции
вокруг боковой стороны,
перпендикулярной
основаниям,
Найдите
площадь
боковой
поверхности усеченного
конуса, если известны
основания
и
боковая
сторона трапеции.
16 10
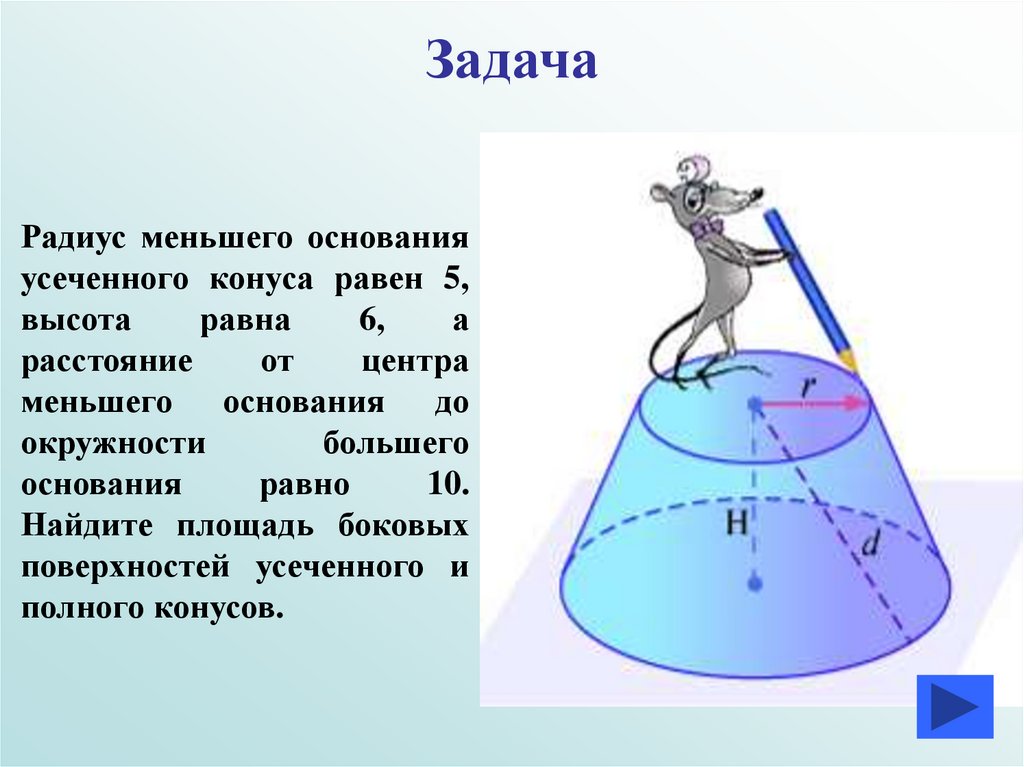
18. Задача
Радиус меньшего основанияусеченного конуса равен 5,
высота
равна
6,
а
расстояние
от
центра
меньшего основания до
окружности
большего
основания
равно
10.
Найдите площадь боковых
поверхностей усеченного и
полного конусов.
19.
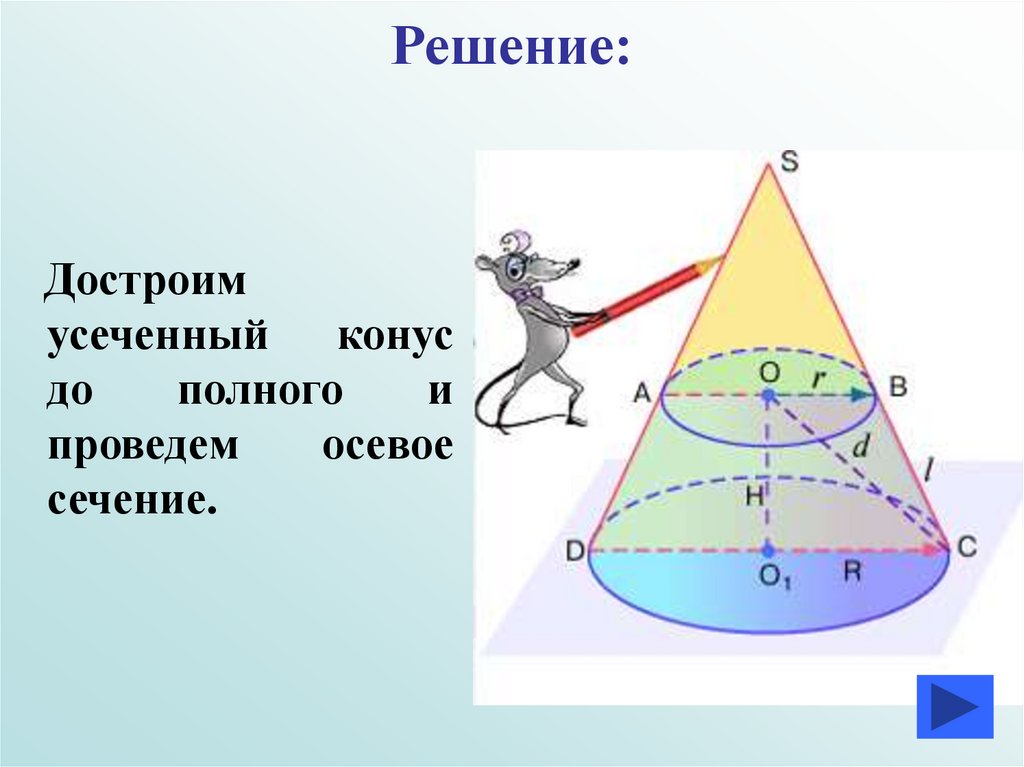
Решение:Достроим
усеченный конус
до
полного
и
проведем
осевое
сечение.
20.
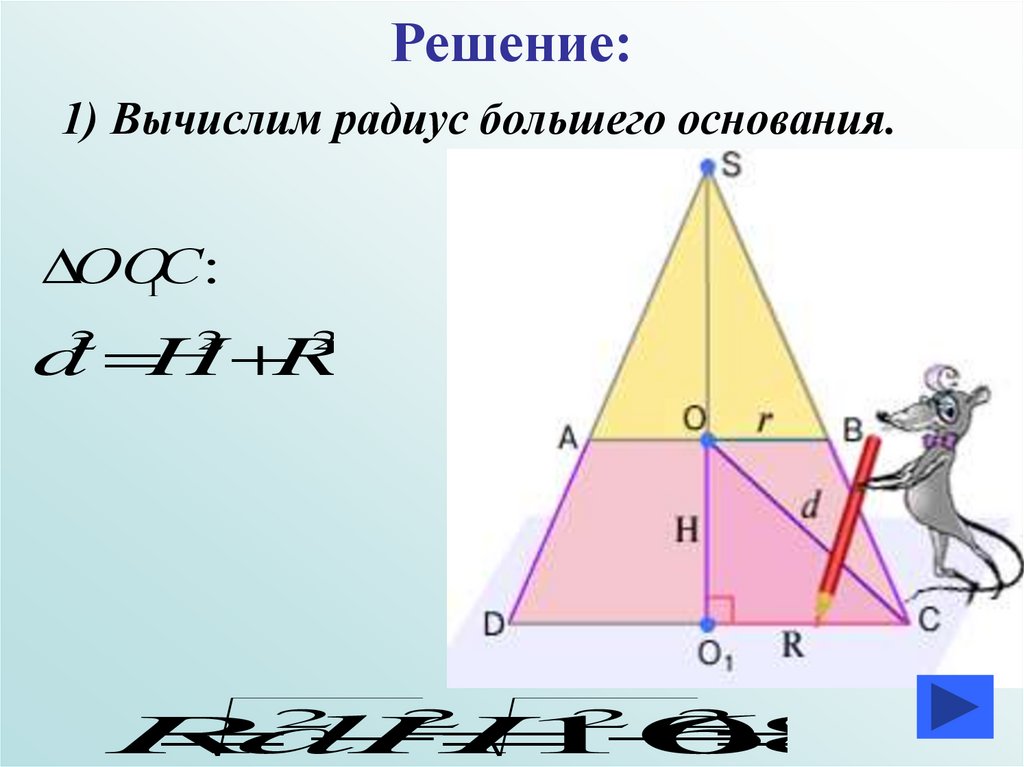
Решение:1) Вычислим радиус большего основания.
ОО1С:
d H R
2
2
2
R
d
H
10
6
8
2
2
2
2
21.
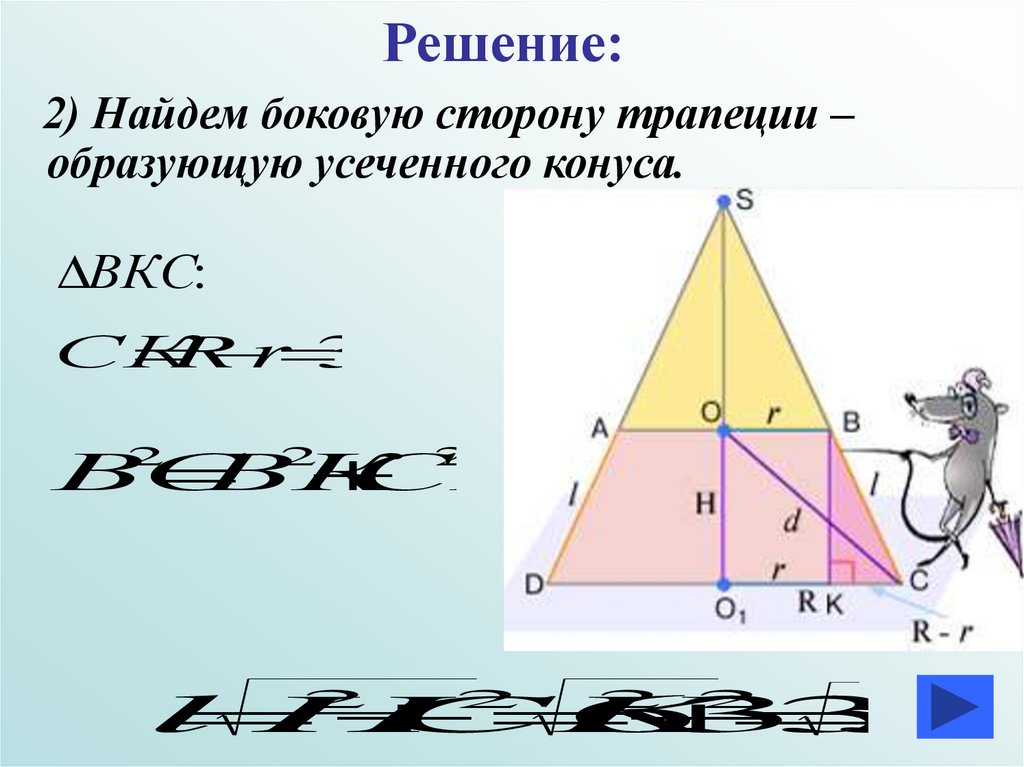
Решение:2) Найдем боковую сторону трапеции –
образующую усеченного конуса.
ВКС:
СК
R
r 3
ВС
ВК
СК
2
2
2
l
H
CK
6
3
3
5
2
2
2
2
22.
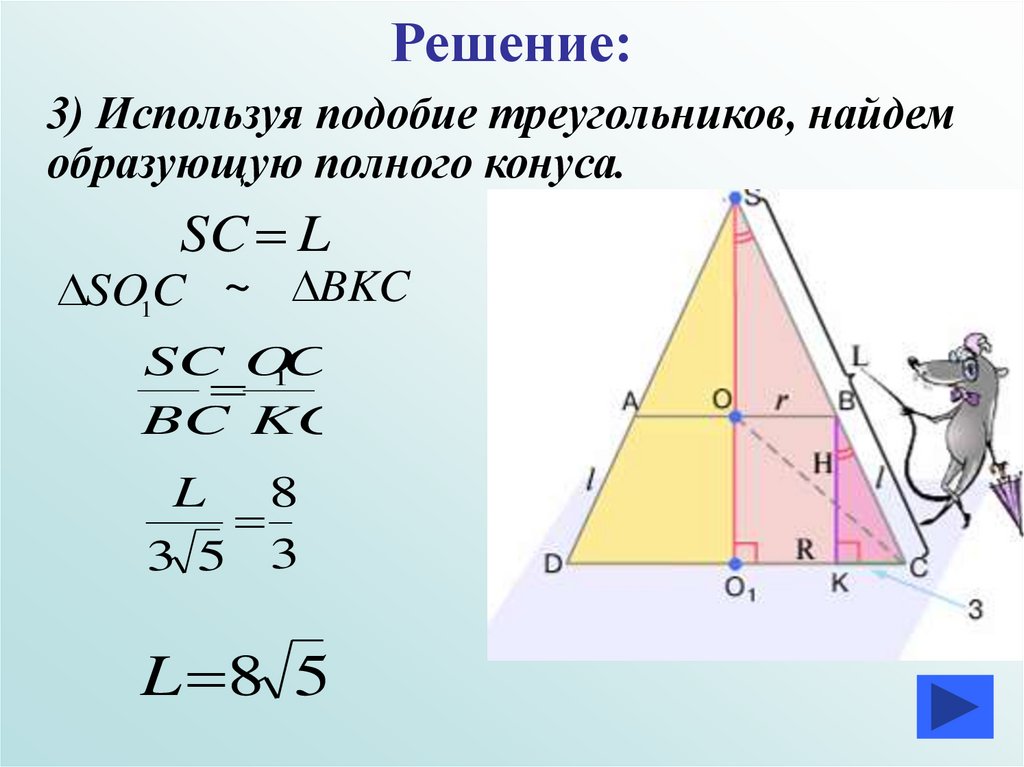
Решение:3) Используя подобие треугольников, найдем
образующую полного конуса.
SC L
SO1C ~ BKC
SC O
1C
BC KC
L 8
3 5 3
L 8 5
23.
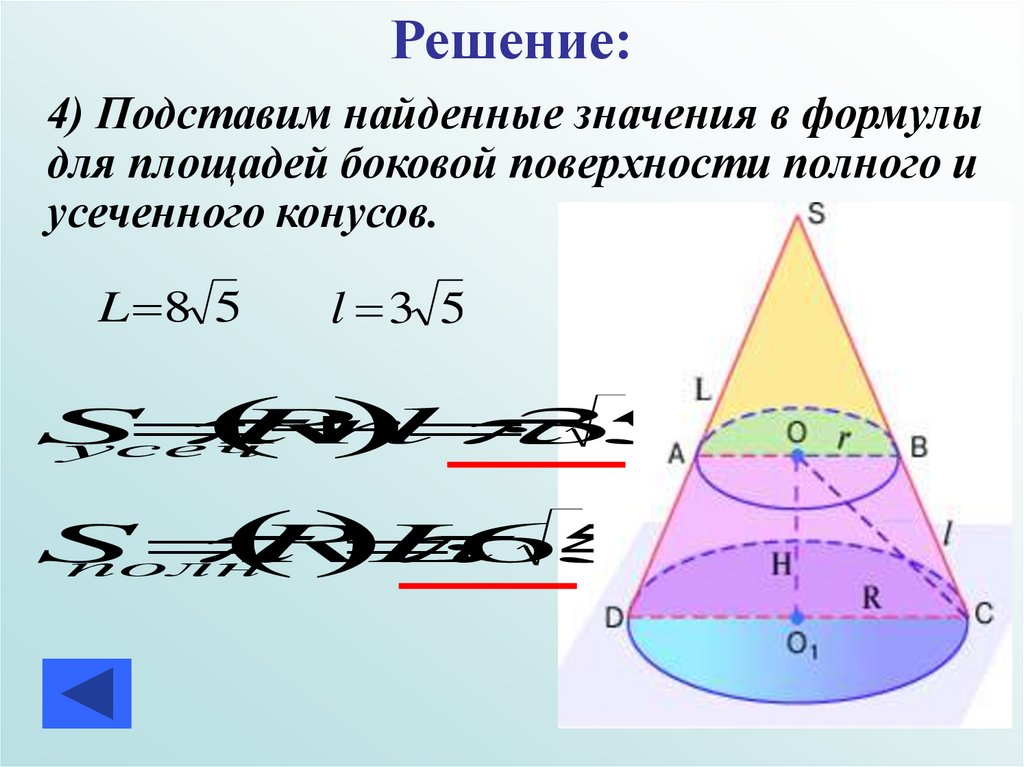
Решение:4) Подставим найденные значения в формулы
для площадей боковой поверхности полного и
усеченного конусов.
L 8 5
l 3 5
S
RL
64
5
S
R
r
l
39
5
усеч
полн
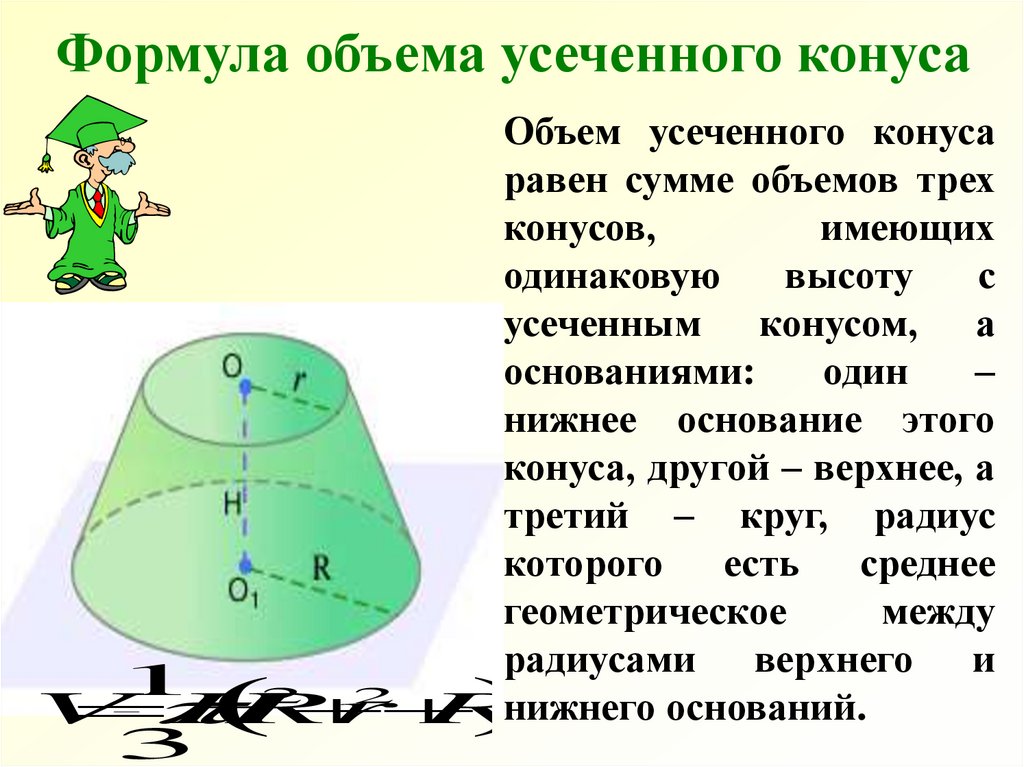
24. Формула объема усеченного конуса
Объем усеченного конусаравен сумме объемов трех
конусов,
имеющих
одинаковую
высоту
с
усеченным конусом, а
основаниями:
один
–
нижнее основание этого
конуса, другой – верхнее, а
третий – круг, радиус
которого есть среднее
геометрическое
между
радиусами верхнего и
1 2 2
нижнего оснований.
V
H
R
r
Rr
3
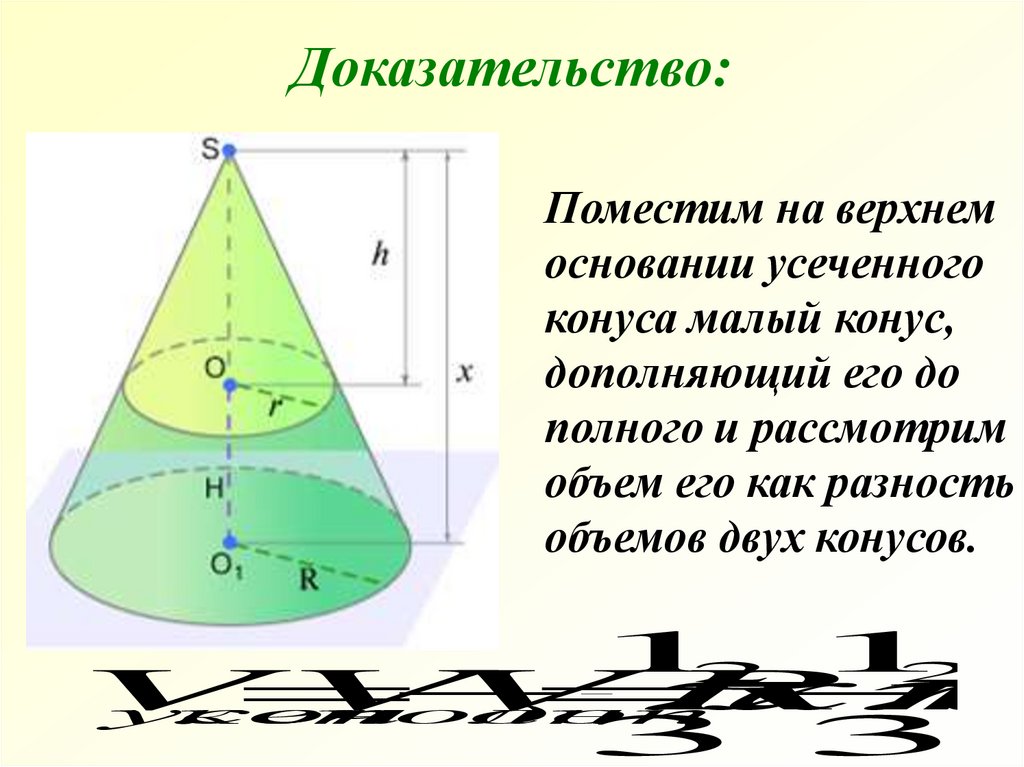
25. Доказательство:
Поместим на верхнемосновании усеченного
конуса малый конус,
дополняющий его до
полного и рассмотрим
объем его как разность
объемов двух конусов.
1
2 1
2
V
V
V
R
x
r
h
усеч
.
кон
полн
доп
3 3
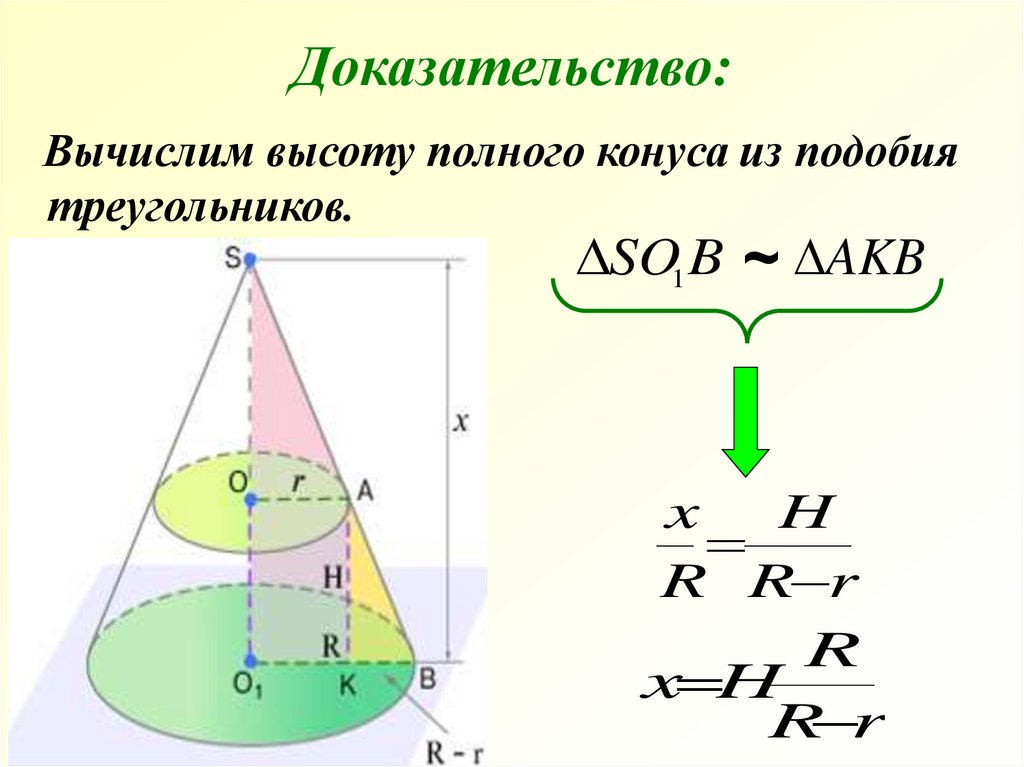
26.
Доказательство:Вычислим высоту полного конуса из подобия
треугольников.
SO1 B ~ AKB
x
H
R R r
R
x H
R r
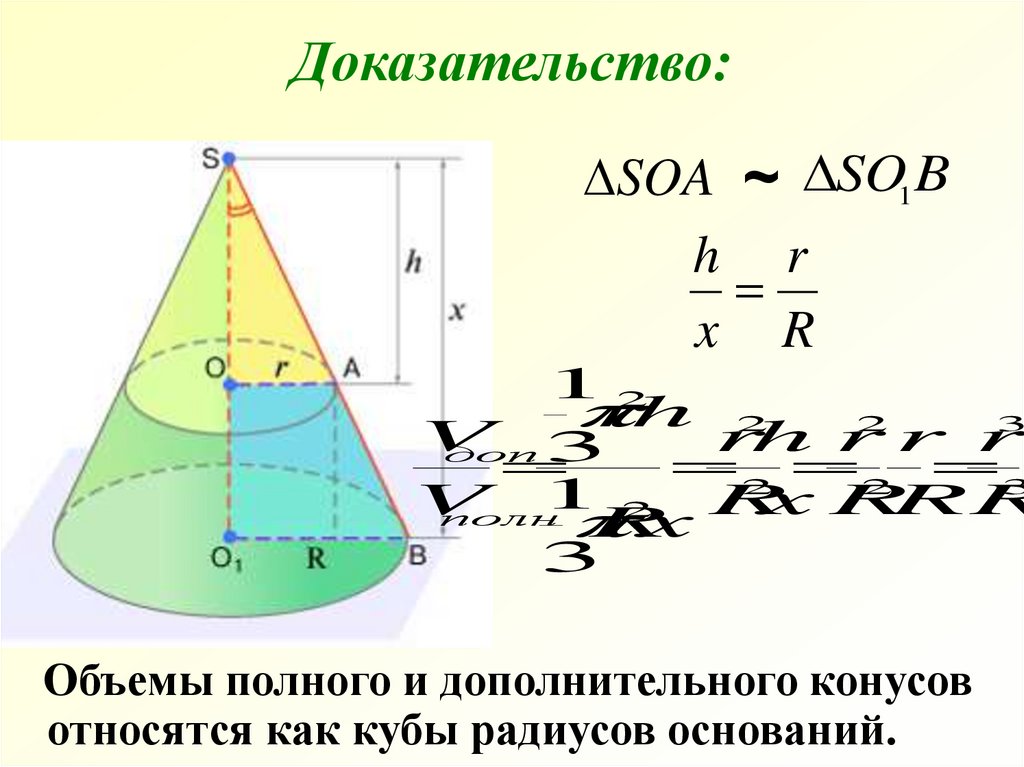
27.
Доказательство:SOA ~ SO1 B
h r
x R
12
rh 2
2
3
V
rh r r r
доп 3
2 2 3
1 2 R
V
x
R
R
R
полн
R
x
3
Объемы полного и дополнительного конусов
относятся как кубы радиусов оснований.
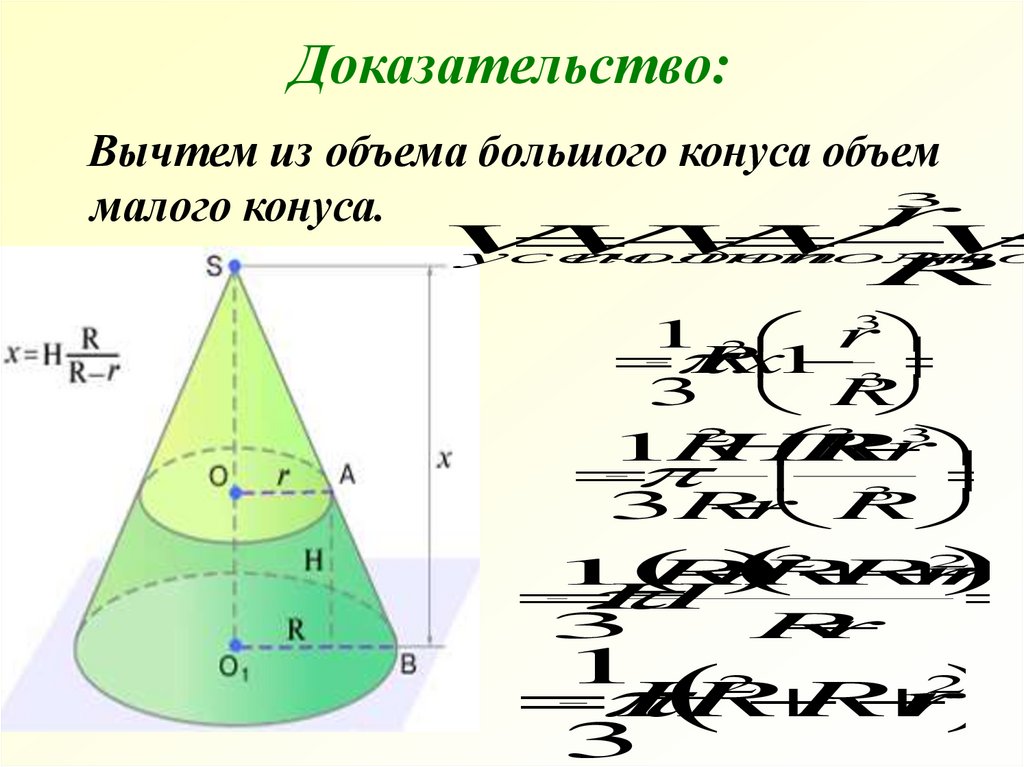
28.
Доказательство:Вычтем из объема большого конуса объем
3
малого конуса.
r
V
V
V
V
V
усеч
полн
доп
полн
3по
R
3
1 2 r
R
x
1
3
3 R
2
3
3
1R
HR
R
r
3
3R
r
R
2
2
1
R
r
R
Rr
r
H
3
R
r
1 2
2
R
H
Rr
r
3
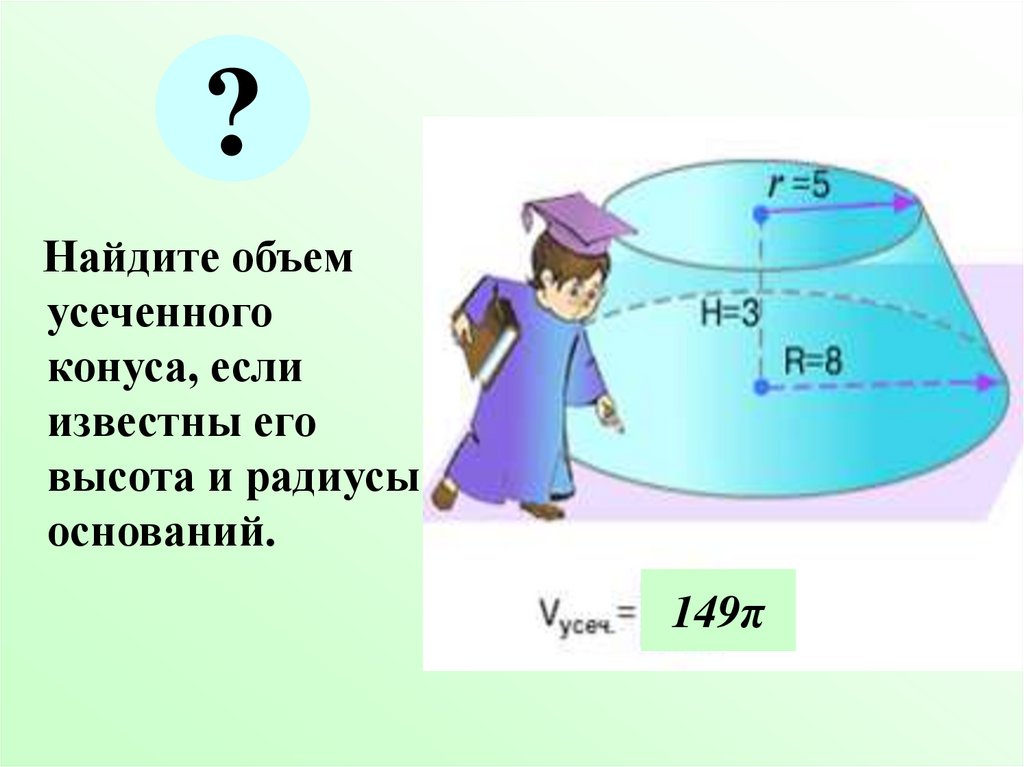
29.
?Найдите объем
усеченного
конуса, если
известны его
высота и радиусы
оснований.
149π
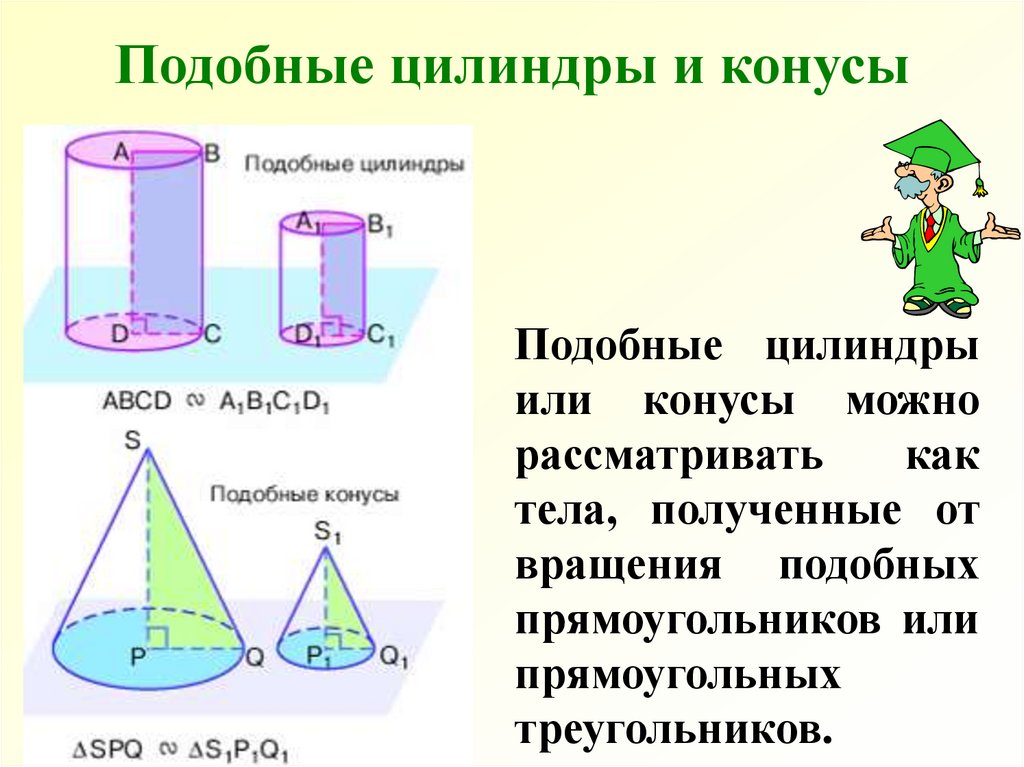
30. Подобные цилиндры и конусы
Подобные цилиндрыили конусы можно
рассматривать
как
тела, полученные от
вращения подобных
прямоугольников или
прямоугольных
треугольников.
31.
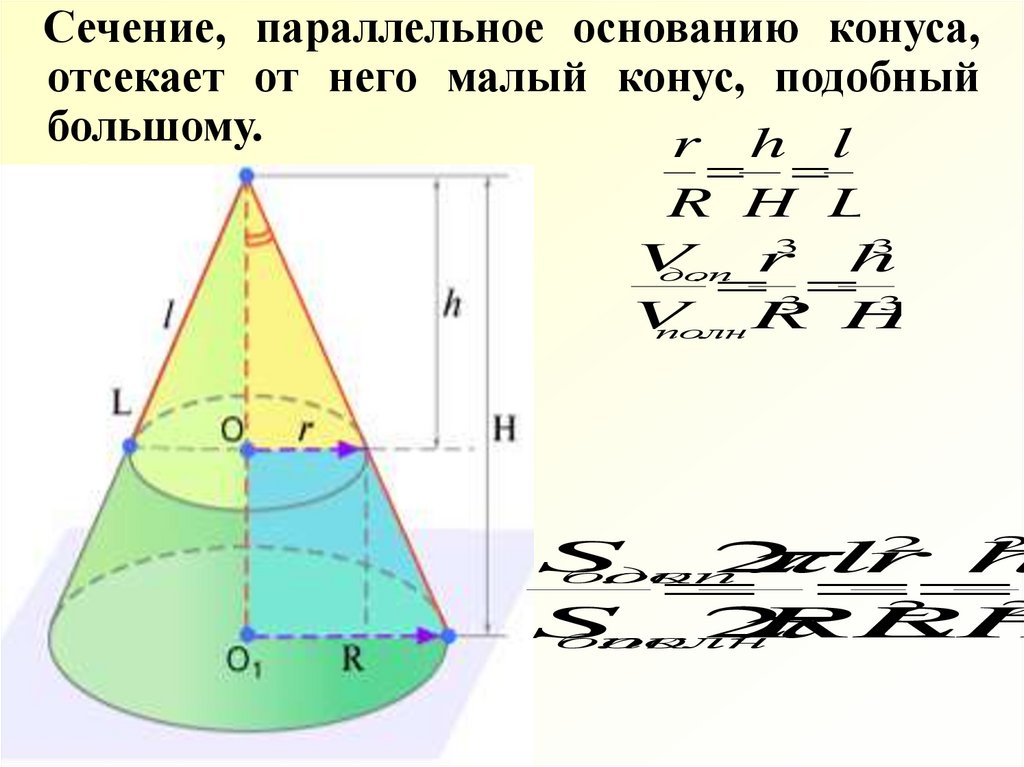
Сечение, параллельное основанию конуса,отсекает от него малый конус, подобный
большому.
r h l
R H L
3
3
V
r
h
доп
.
3 3
V
R H
полн
.
2
2
S
2
rlr h
бок
.
доп
2
2
S
2
RL
RH
бок
.
полн
32.
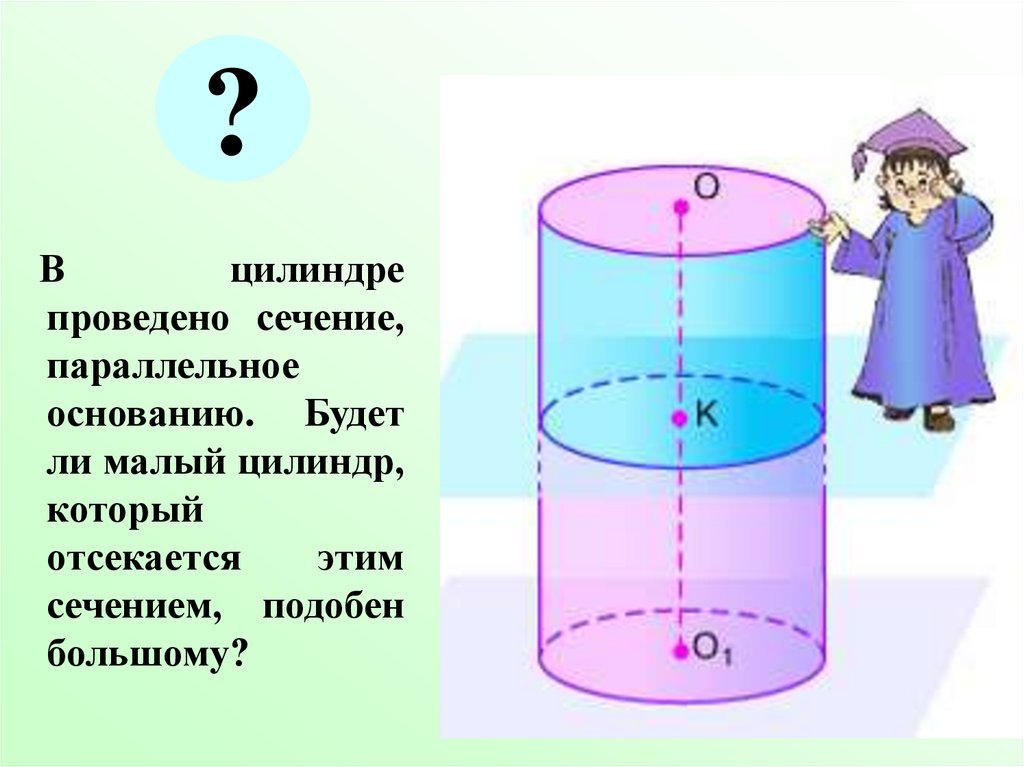
?В
цилиндре
проведено сечение,
параллельное
основанию. Будет
ли малый цилиндр,
который
отсекается
этим
сечением, подобен
большому?
33.
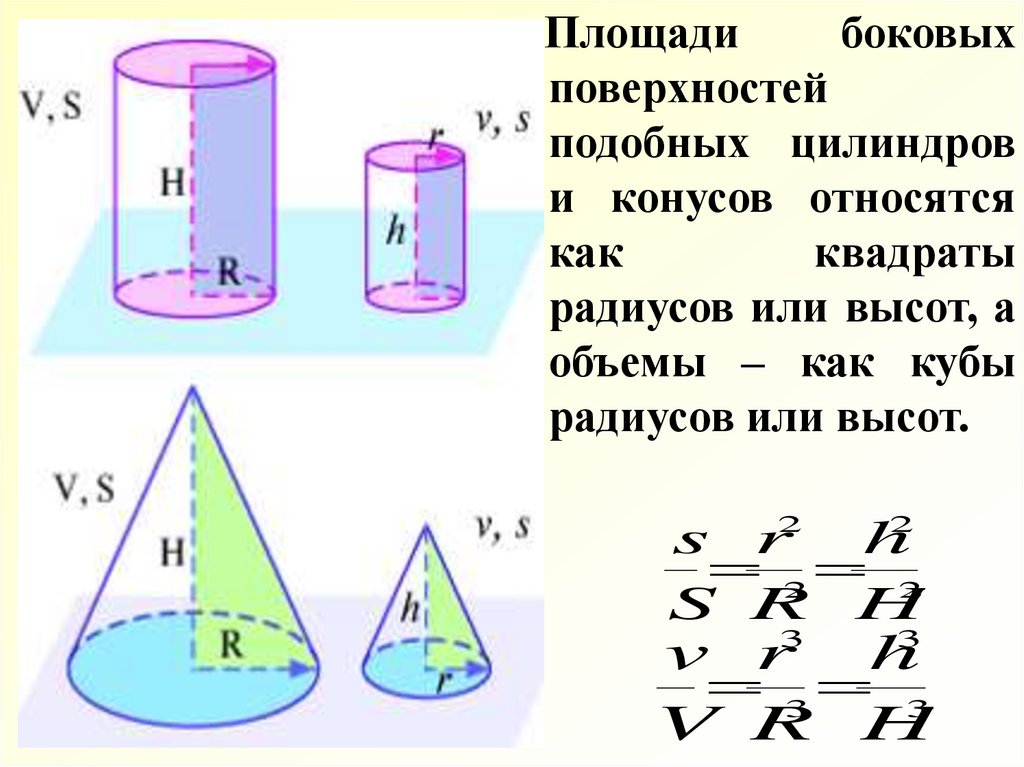
Площадибоковых
поверхностей
подобных цилиндров
и конусов относятся
как
квадраты
радиусов или высот, а
объемы – как кубы
радиусов или высот.
2
2
3
3
s r
h
2 2
S R H
v r h
3 3
V R H
34.
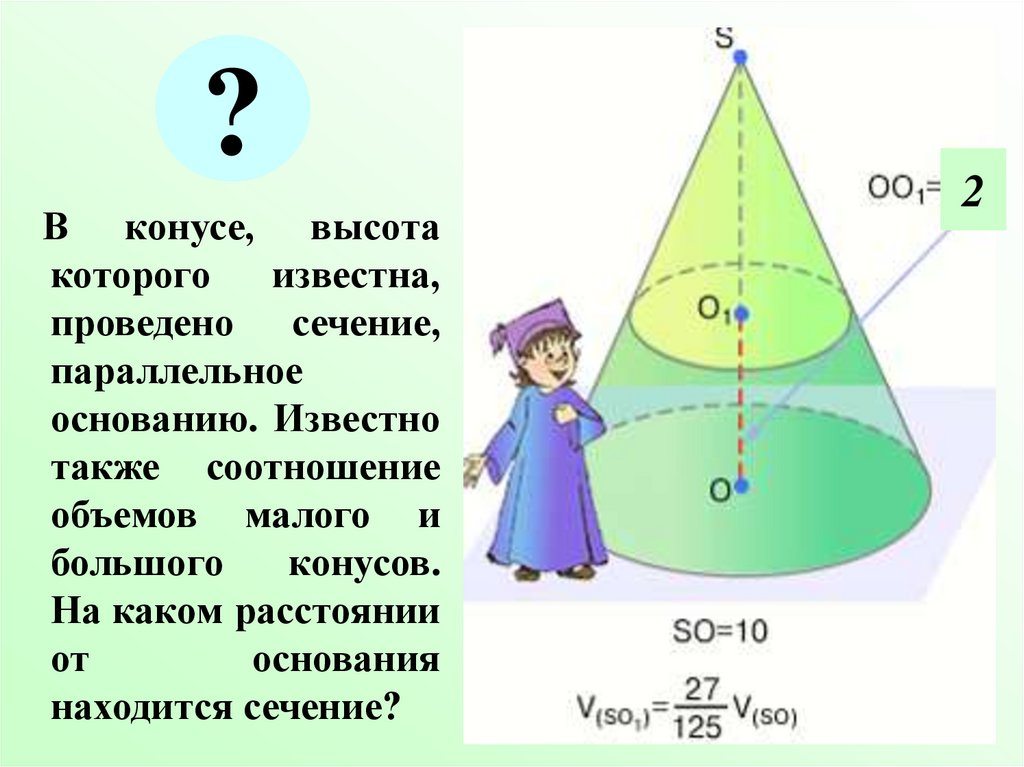
?В конусе, высота
которого
известна,
проведено сечение,
параллельное
основанию. Известно
также соотношение
объемов малого и
большого
конусов.
На каком расстоянии
от
основания
находится сечение?
2
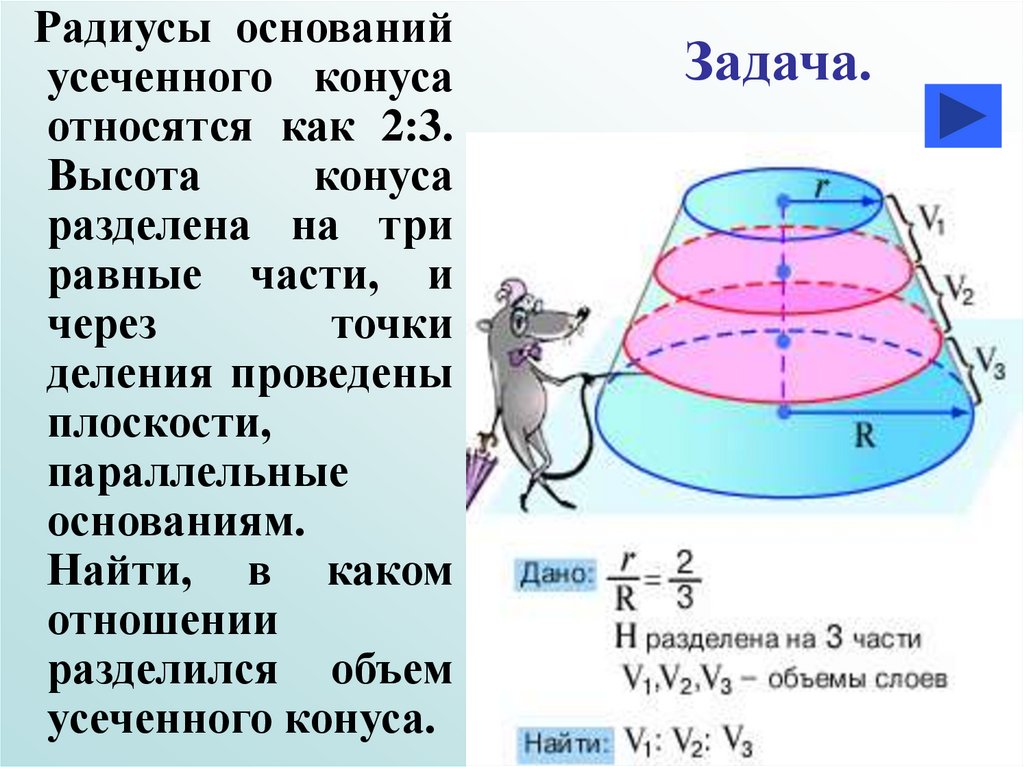
35.
Радиусы основанийусеченного конуса
относятся как 2:3.
Высота
конуса
разделена на три
равные части, и
через
точки
деления проведены
плоскости,
параллельные
основаниям.
Найти, в каком
отношении
разделился объем
усеченного конуса.
Задача.
36.
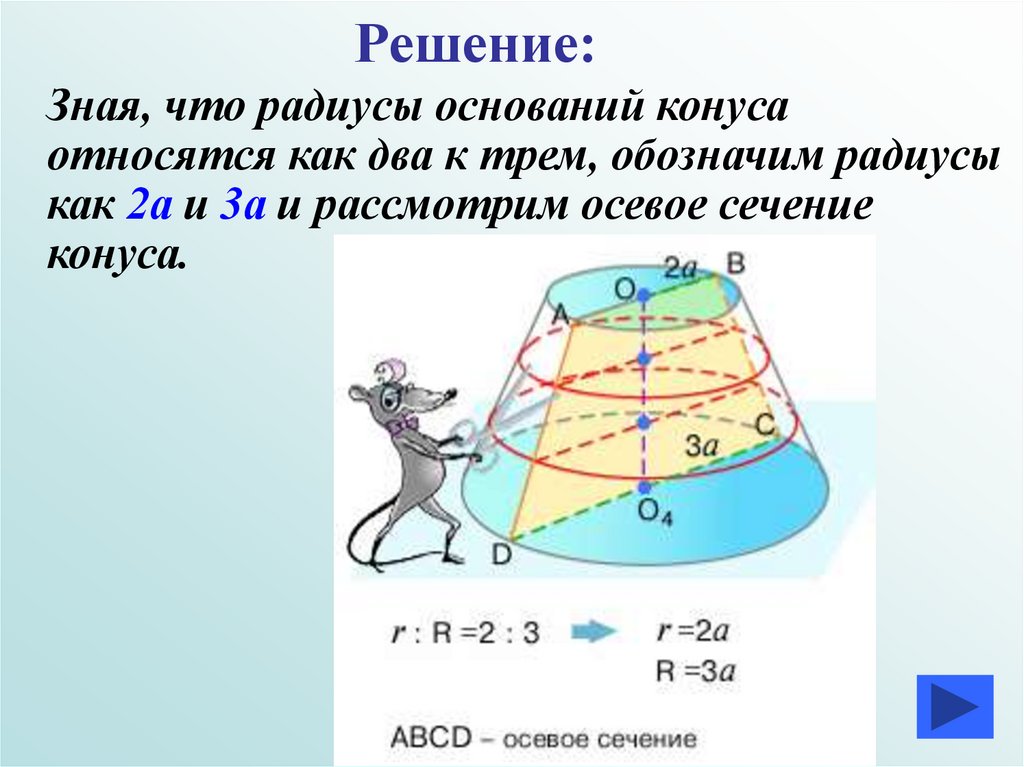
Решение:Зная, что радиусы оснований конуса
относятся как два к трем, обозначим радиусы
как 2а и 3а и рассмотрим осевое сечение
конуса.
37.
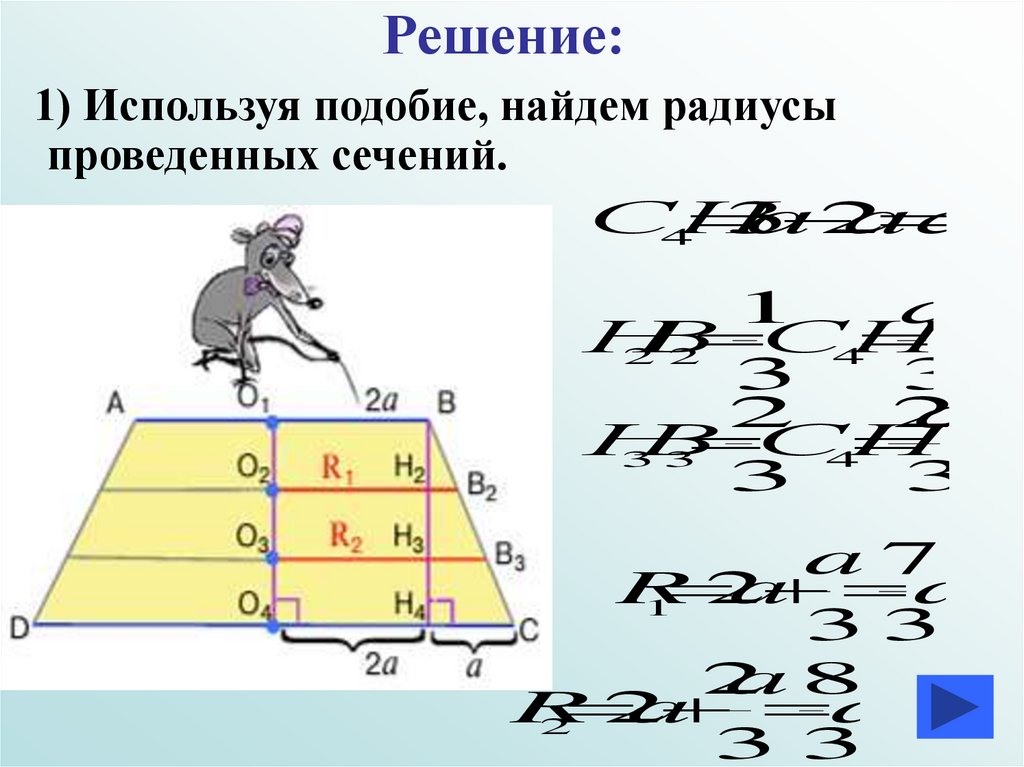
Решение:1) Используя подобие, найдем радиусы
проведенных сечений.
СН
3
а
2
а
а
4
1
а
Н
В
2
2 СН
4
3
3
2
2
а
Н
В
3
3 СН
4
3
3
a7
R
2
a
a
1
33
2
a8
R
2
a
a
2
3 3
38.
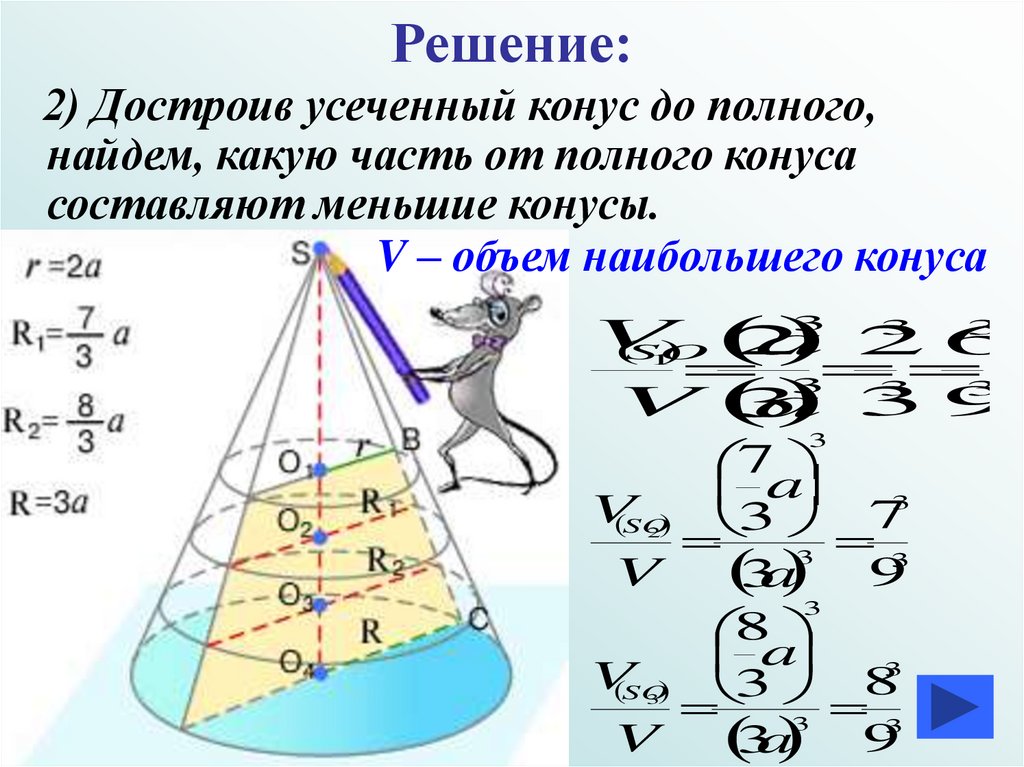
Решение:2) Достроив усеченный конус до полного,
найдем, какую часть от полного конуса
составляют меньшие конусы.
V – объем наибольшего конуса
3
3
3
V
2
a
26
SO
3 3 3
V
39
3
a
1
3
7
a
3
V
7
3
SO
3
3
V
3a 9
3
8
a
3
V
8
3
SO
3
3
V
3a 9
2
3
39.
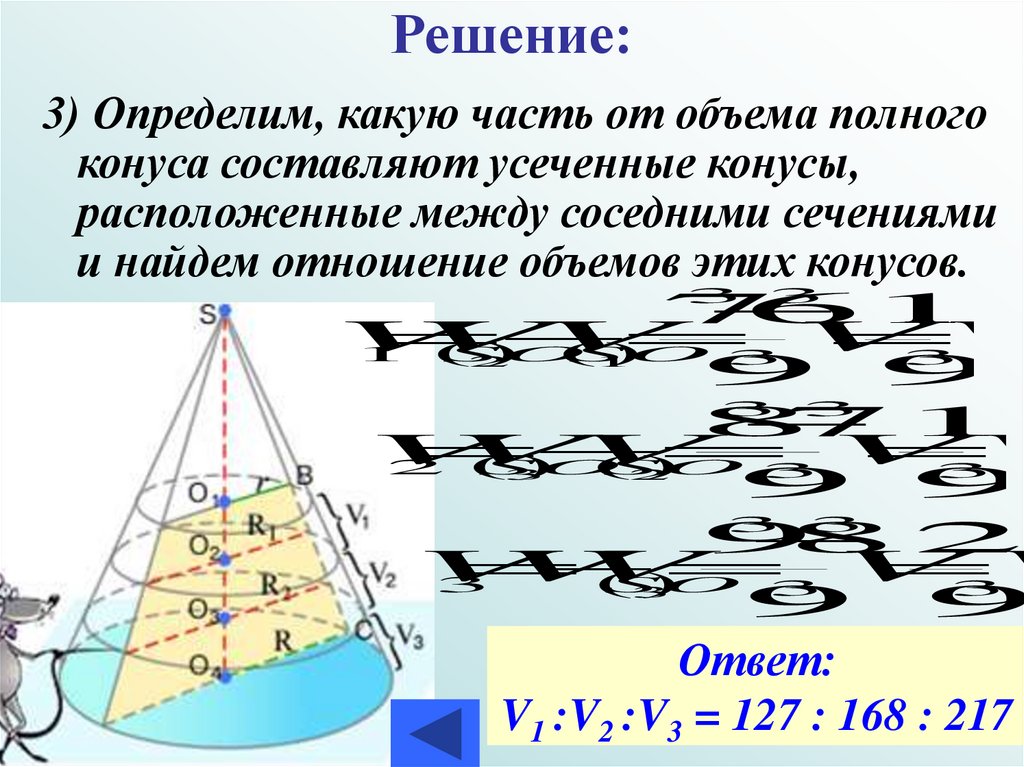
Решение:3) Определим, какую часть от объема полного
конуса составляют усеченные конусы,
расположенные между соседними сечениями
и найдем отношение объемов этих конусов.
3 3
7
612
V
V
V
V
V
1
SO
SO
3
3
9 9
3 3
8
716
V
V
V
V
V
2
SO
SO
3
3
9 9
3 3
9
8 21
V
V
V
3 V
V
3
SO
3
9
9
Ответ:
V1 :V2 :V3 = 127 : 168 : 217
2
3
1
2
3






 mathematics
mathematics