geo_7_treug_2

1.

2.

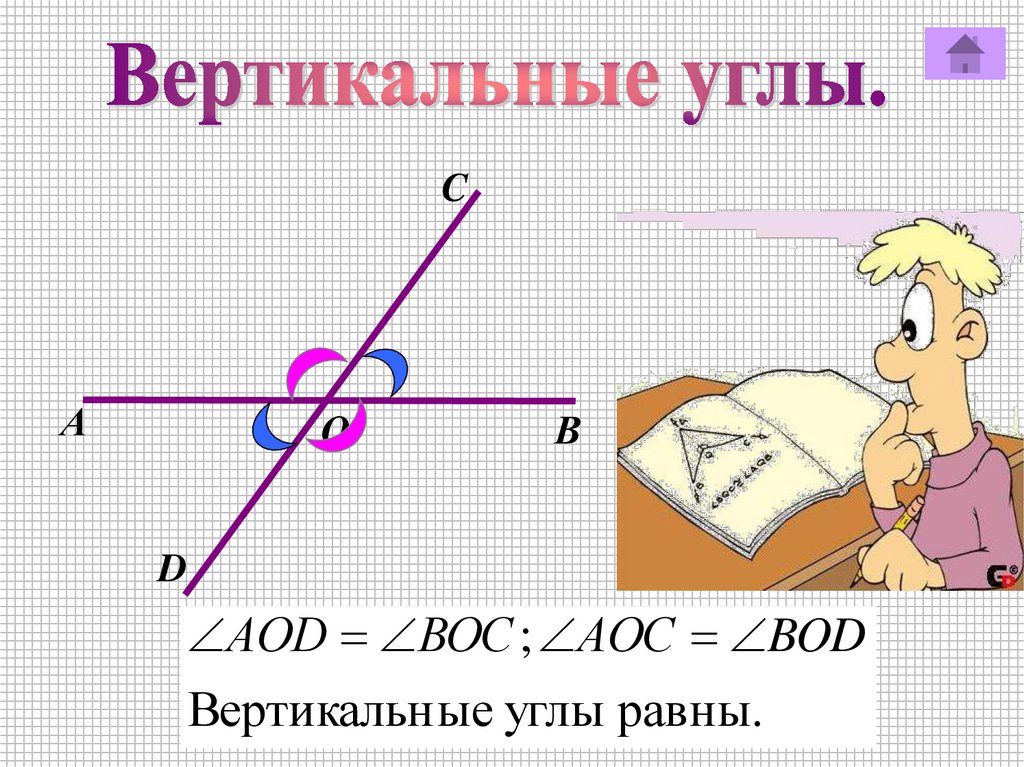
C
А
О
В
D
АОD ВОC ; АОС BOD
Вертикальн ые углы равны.

3.

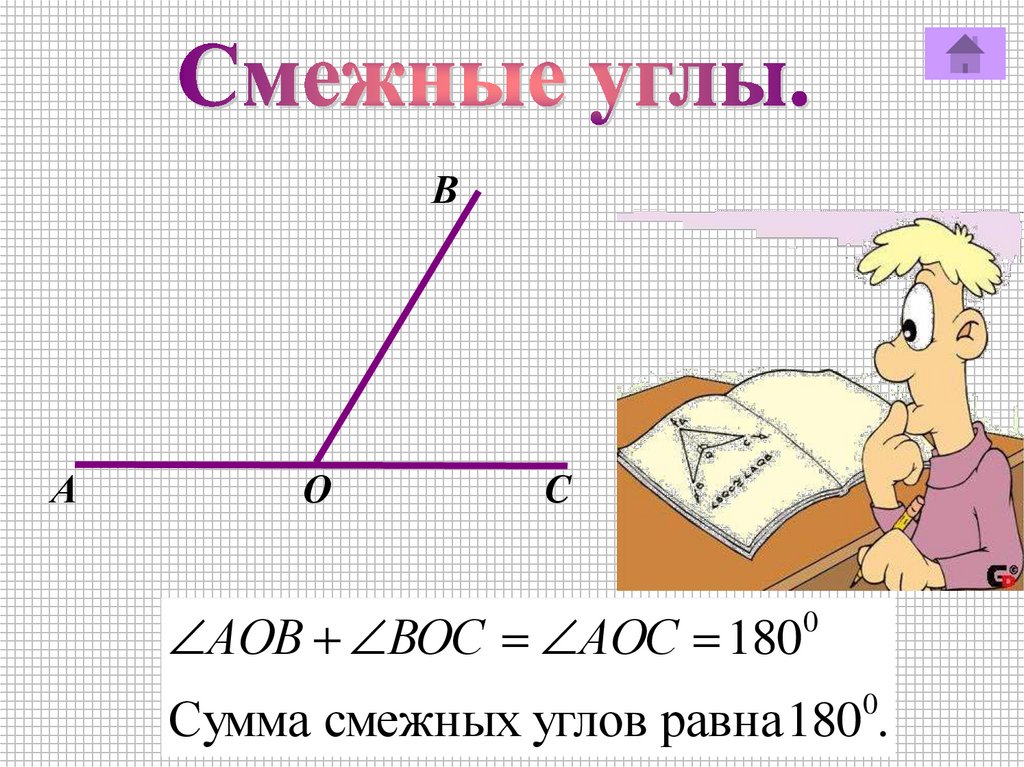
В
А
О
C
АОB ВОC АОС 180
0
Сумма смежных углов равна 180 .
0

4.

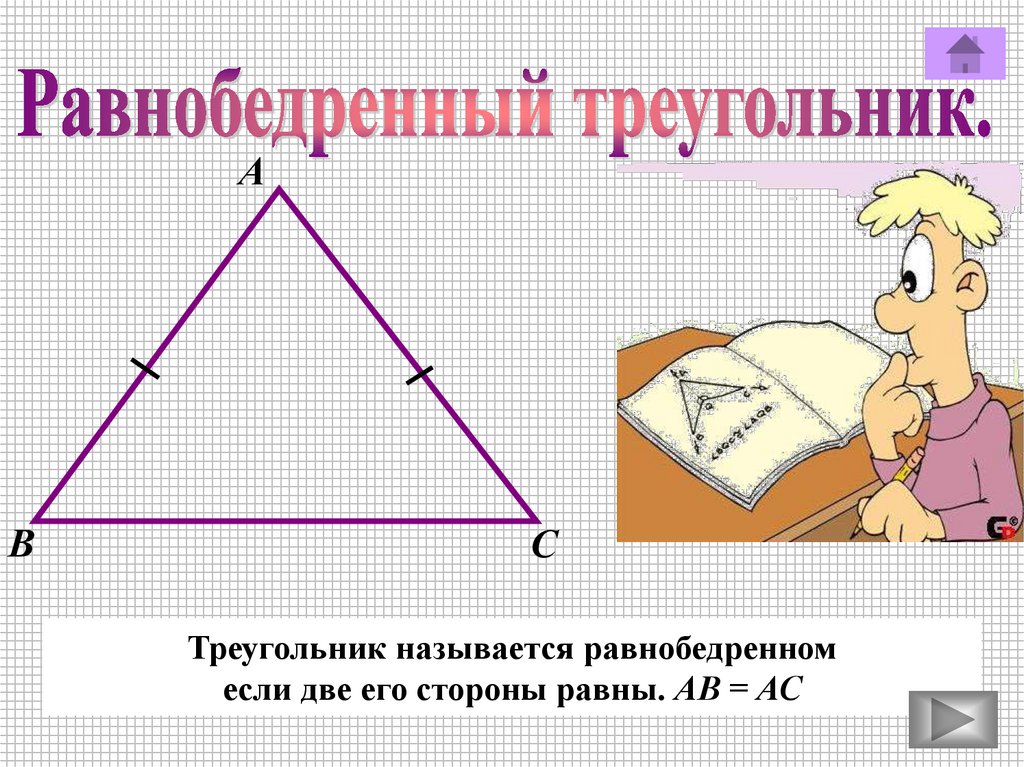
А
В
С
Треугольник называется равнобедренном
если две его стороны равны. АВ = АС

5.

А
В
М
С
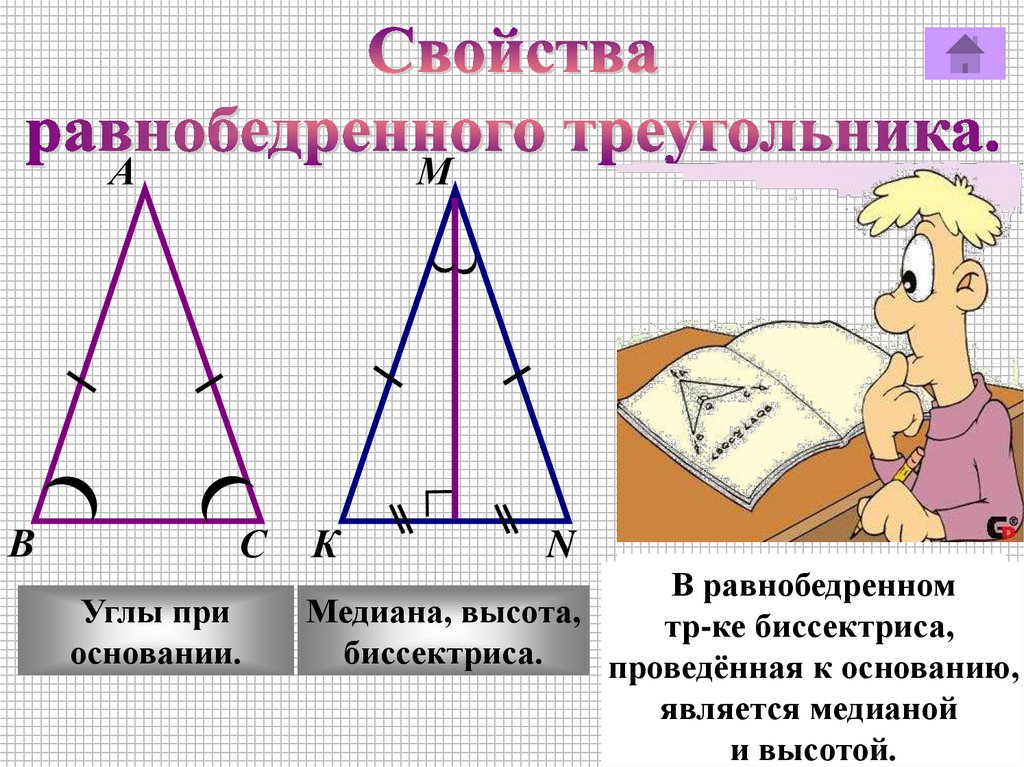
Углы при
основании.
К
N
В равнобедренном
Медиана, высота,
В равнобедренном
тр-ке
биссектриса,
биссектриса.
треугольнике
углы
проведённая
к основанию,
при
основании
равны.
является
медианой
и высотой.

6.

А
А1
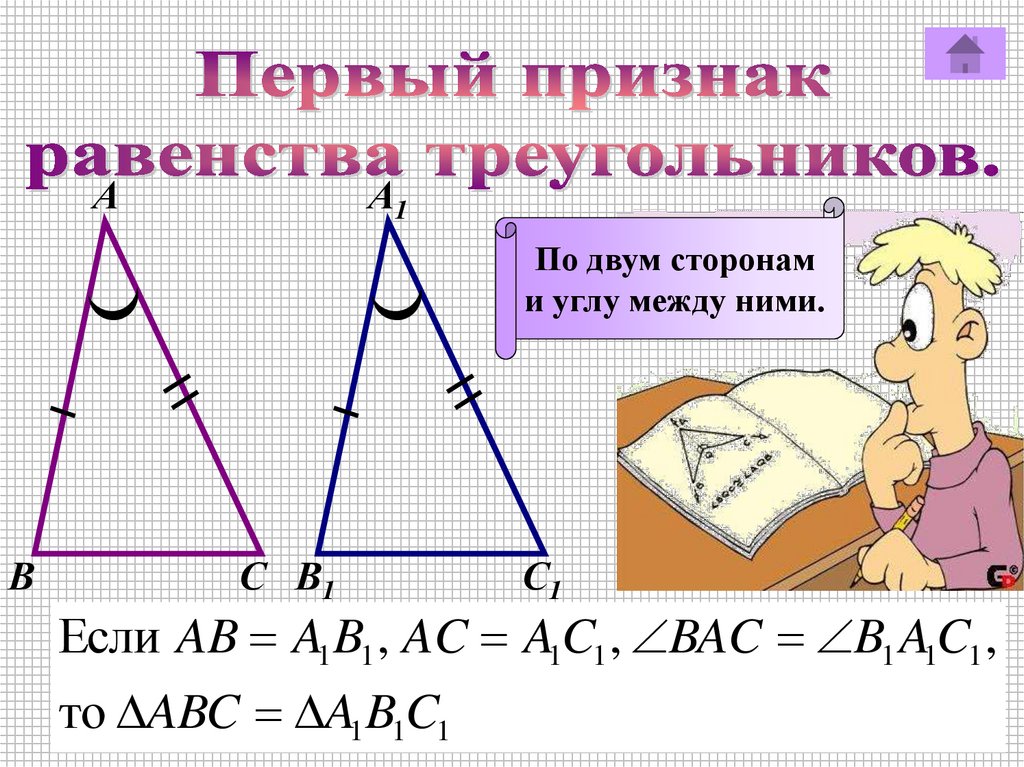
По двум сторонам
и углу между ними.
В
С В1
С1
Если AB A1 B1 , AC A1C1 , BAC B1 A1C1 ,
то ABC A1 B1C1

7.

А
В
А1
С В1
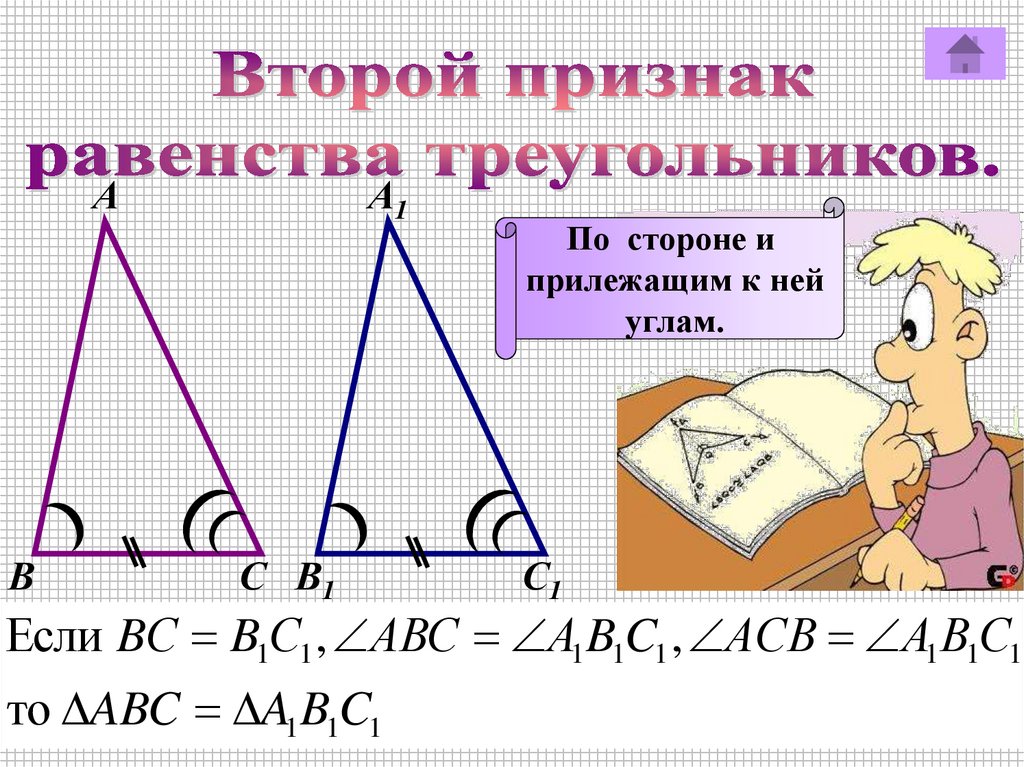
По стороне и
прилежащим к ней
углам.
С1
Если BС B1С1 , АBC А1 B1C1 , АСВ А1 В1С1
то ABC A1 B1C1

8.

А
А1
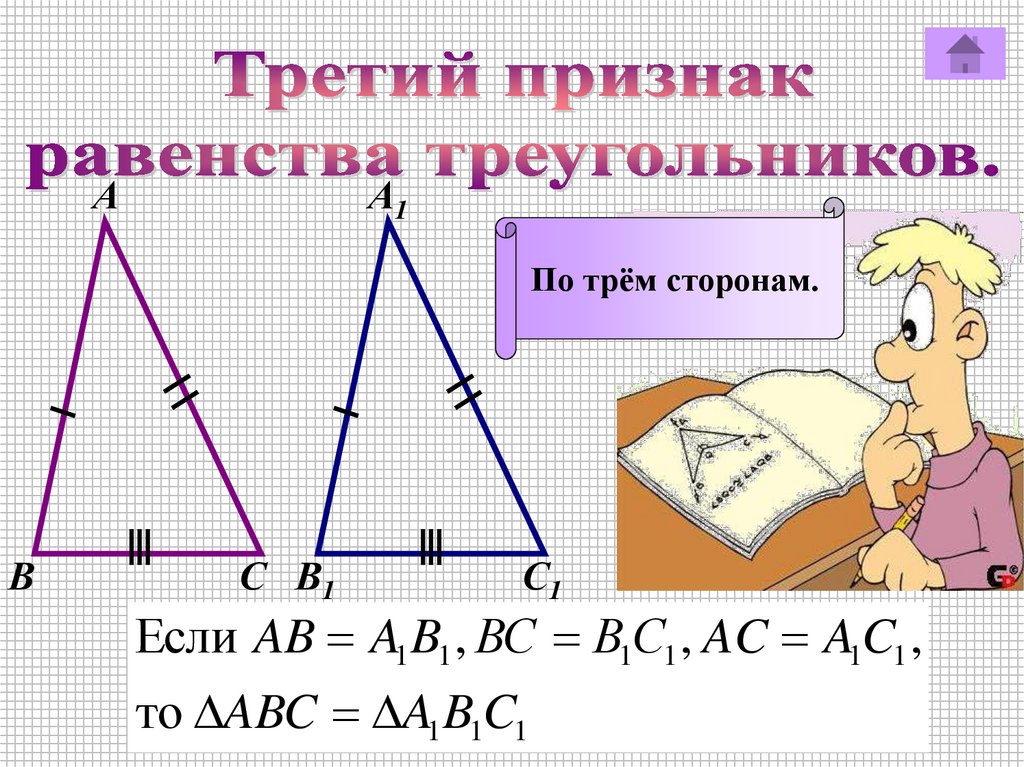
По трём сторонам.
В
С В1
С1
Если AB A1 B1 , ВС В1С1 , AC A1C1 ,
то ABC A1 B1C1

9. Задание от 12.11

Выполнить решение задачи №1,2,3,4
придерживаясь общей структуры
решения геометрических задач(т.е. в
тетради должно быть: дано, чертеж,
найти(доказать),
решение(доказательство), ответ (что и
требовалось доказать)
Фото решения прислать на почту
[email protected]
Не забудьте подписать работу!!!

10.

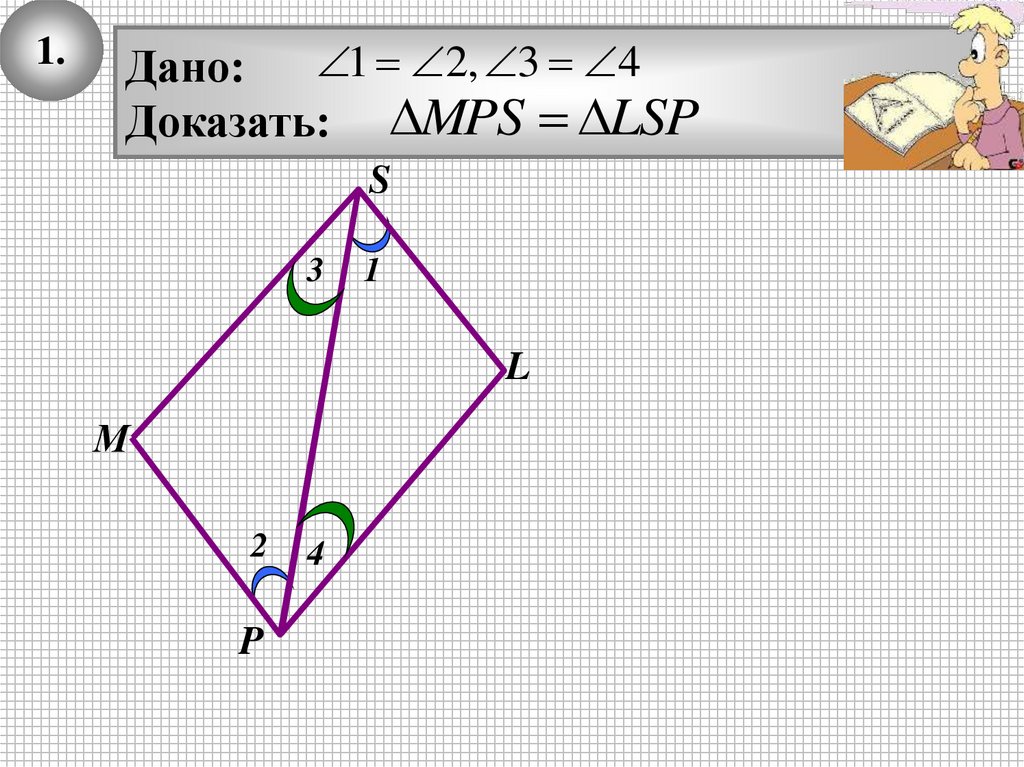
1.
1 2, 3 4
Дано:
Доказать: MPS LSP
S
3
1
L
М
2
P
4

11.

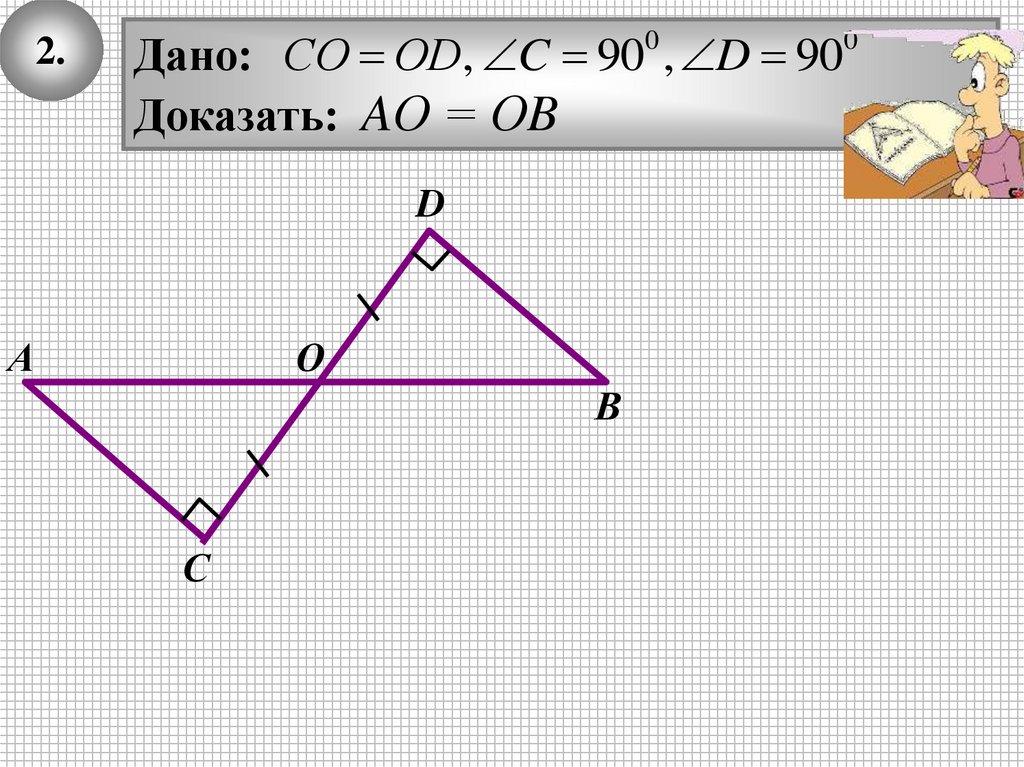
2.
Дано: СО ОD, C 90 , D 90
Доказать: AО = ОB
0
D
А
О
В
С
0

12.

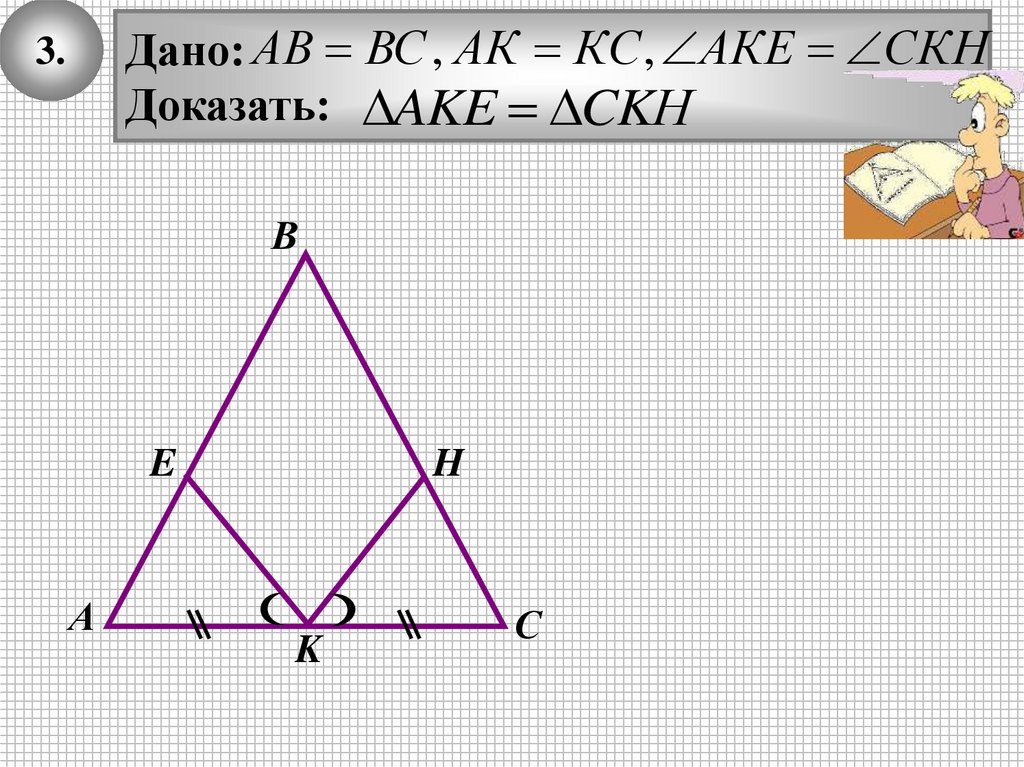
Дано: АB ВС , АК КС, АКЕ СКН
Доказать: AKE CKН
3.
В
E
А
H
K
С

13.

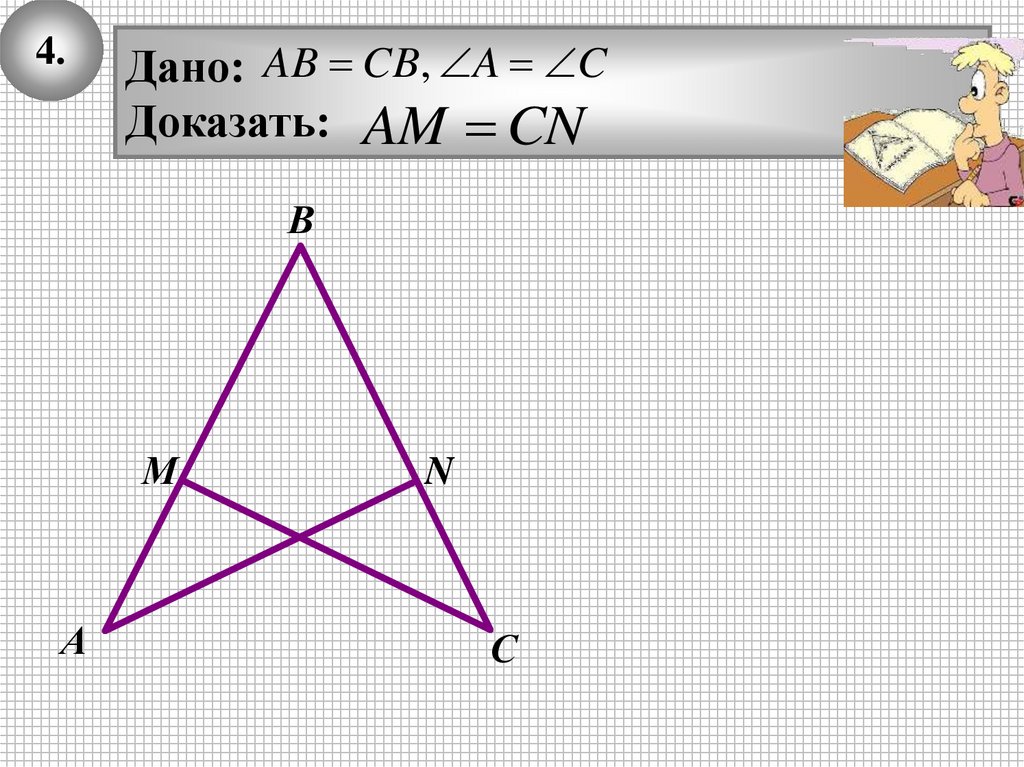
4.
Дано: AB CB, A C
Доказать: AM CN
В
М
А
N
С

14. Задание от 14.11

Выполнить решение задачи №5,6,7
придерживаясь общей структуры
решения геометрических задач(т.е. в
тетради должно быть: дано, чертеж,
найти(доказать),
решение(доказательство), ответ (что и
требовалось доказать)
Фото решения прислать на почту
[email protected]
Не забудьте подписать работу!!!

15.

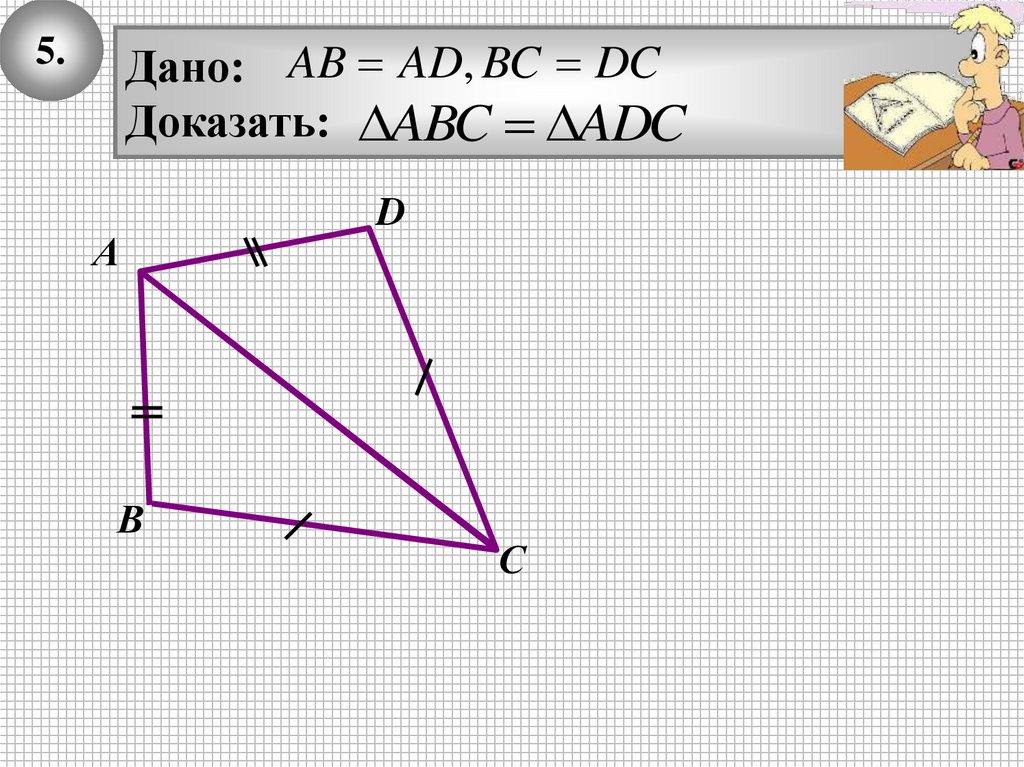
Дано: AB AD, BC DC
Доказать: ABC ADC
5.
А
В
D
С

16.

Дано: AB AК , BCD KFD
Доказать: ACК AFB
6.
С
В
D
А
K
F

17.

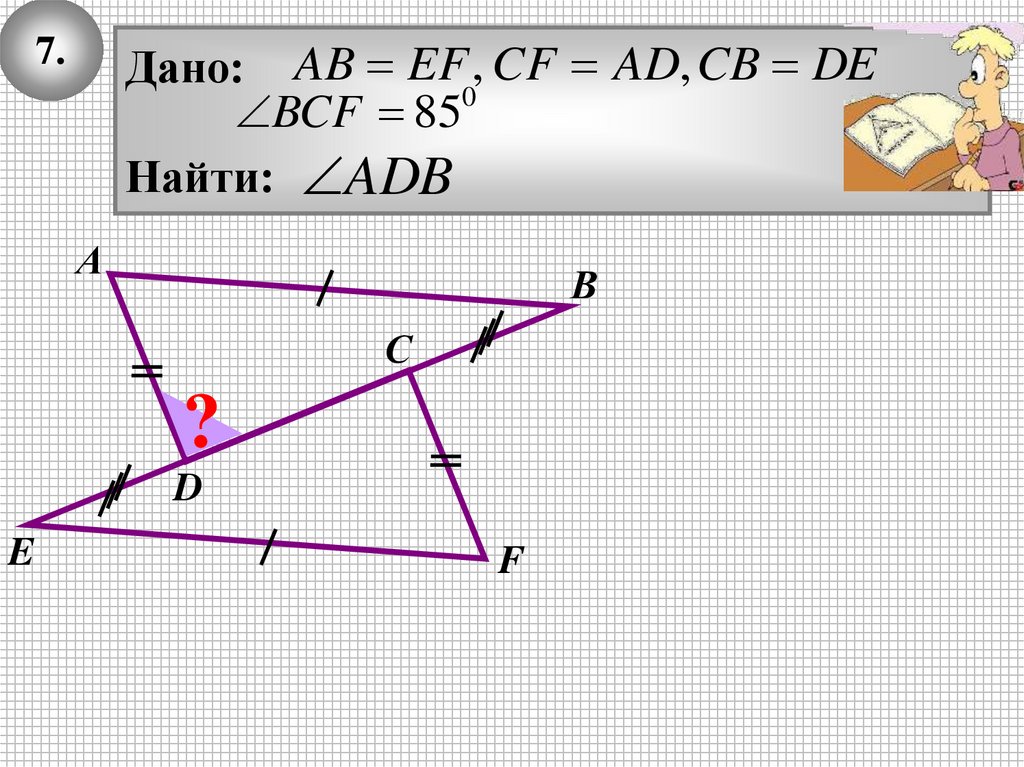
Дано: AB EF , CF AD, CB DE
0
BCF 85
Найти: ADB
7.
А
В
С
?
D
E
F