2.16M

Category: $mathematics$ mathematics

Декартовы координаты в пространстве. Понятие вектора в пространстве. Действия с векторами_ (10-11 класс)

1.

Декартовы координаты в пространстве.
Понятие вектора в пространстве.
Действия с векторами.
2024

Декартовы координаты в пространстве
Прямоугольная система координат в пространстве образована
тремя попарно перпендикулярными прямыми, с выбранными
направлениями и единицами измерения.
z
1
0
x
1
1
y
Ох – ось абсцисс;
Оy – ось ординат;
Оz – ось аппликат;
Oxyz

3.

Декартовы координаты в пространстве.
z
z
Оху
1
1
0
1
0
1
1
y
x
x 1
z
1
х
Оуz
1
Оzх
0
1
y
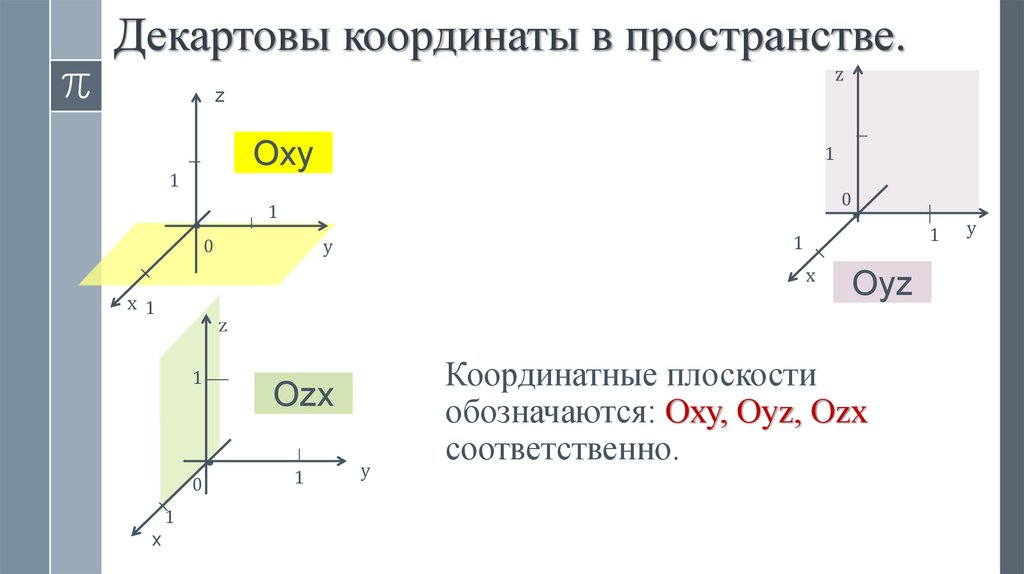
Координатные плоскости
обозначаются: Оху, Оуz, Оzх
соответственно.
y

4.

Декартовы
координаты в пространстве.
z
y
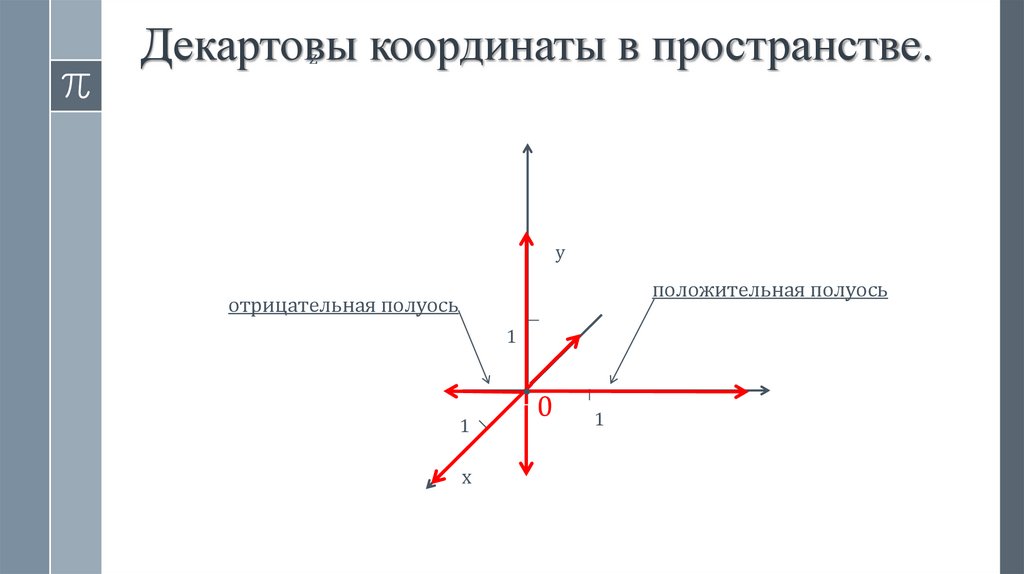
положительная полуось
отрицательная полуось
1
1
x
0
1

5.

z
M
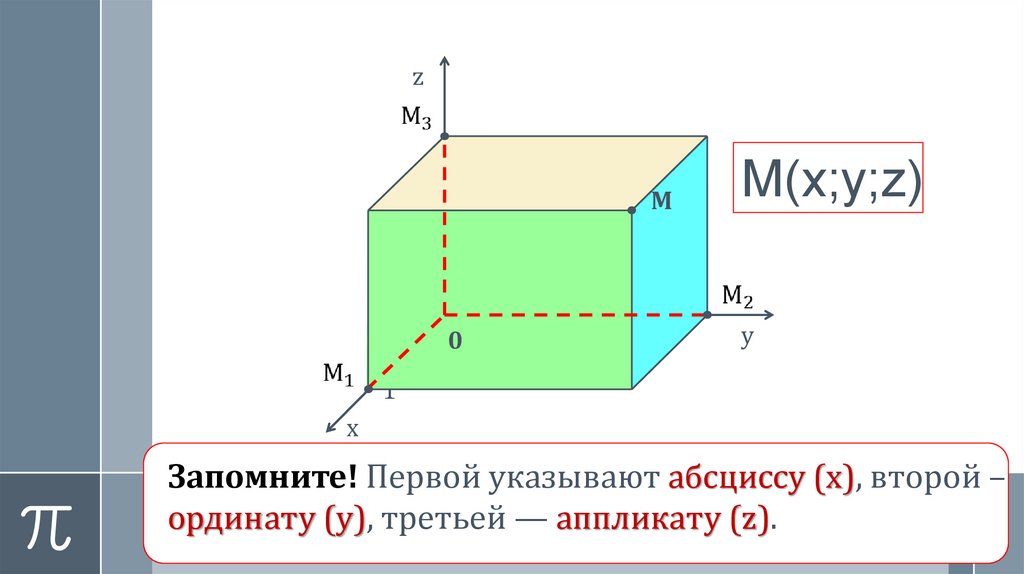
М(х;у;z)
1
00
1
y
1
x
Запомните! Первой указывают абсциссу (х), второй –
ординату (у), третьей — аппликату (z).

6.

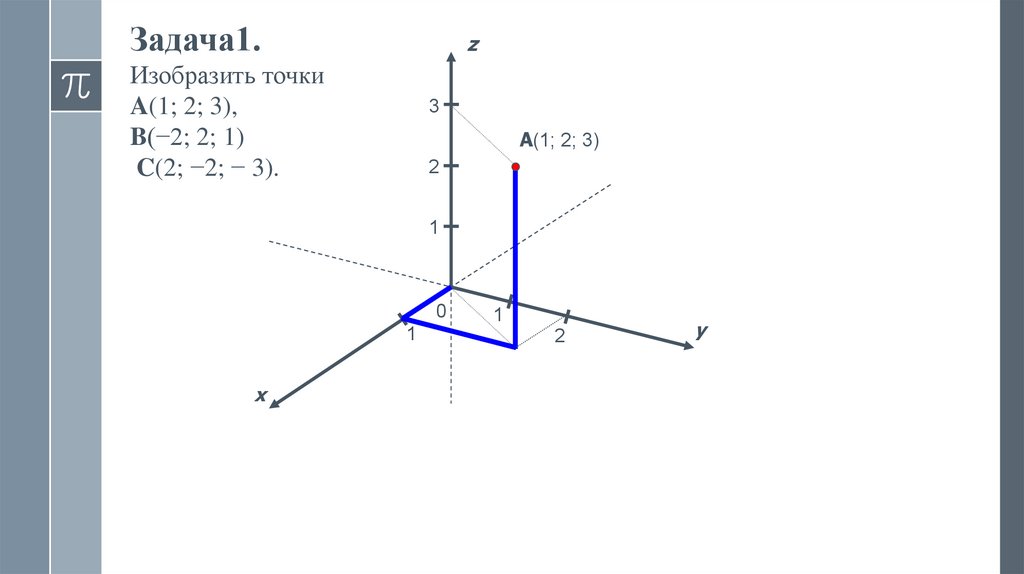
Задача1.
z
Изобразить точки
A(1; 2; 3),
B(−2; 2; 1)
C(2; −2; − 3).
3
A(1; 2; 3)
2
1
0
1
x
1
2
y

7.

z
3
A(1; 2; 3)
A
2
B
1
−2
B(−2; 2; 1)
−2
C(2; −2; − 3)
0
1
1
2
2
x
−3
C
y

8.

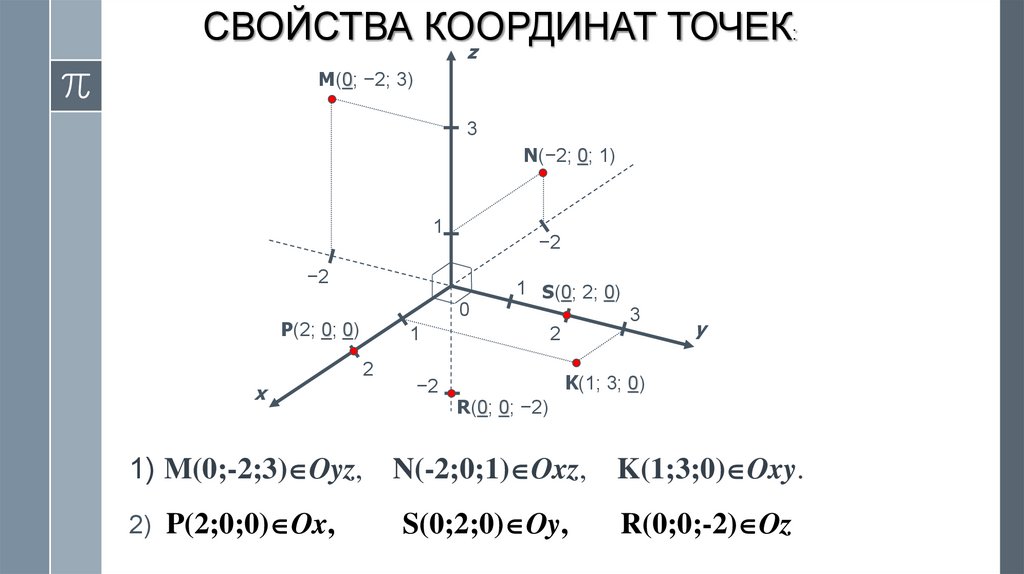
СВОЙСТВА КООРДИНАТ
ТОЧЕК
:
z
M(0; −2; 3)
3
N(−2; 0; 1)
1
−2
−2
1 S(0; 2; 0)
0
P(2; 0; 0)
1
2
x
−2
3
2
y
K(1; 3; 0)
R(0; 0; −2)
1) M(0;-2;3) Oyz, N(-2;0;1) Oxz,
K(1;3;0) Oxy.
2) P(2;0;0) Ox,
R(0;0;-2) Oz
S(0;2;0) Oy,

9.

Вектора на плоскости

10.

Определение вектора. Координаты вектора.
Вектор - это направленный отрезок.

11.

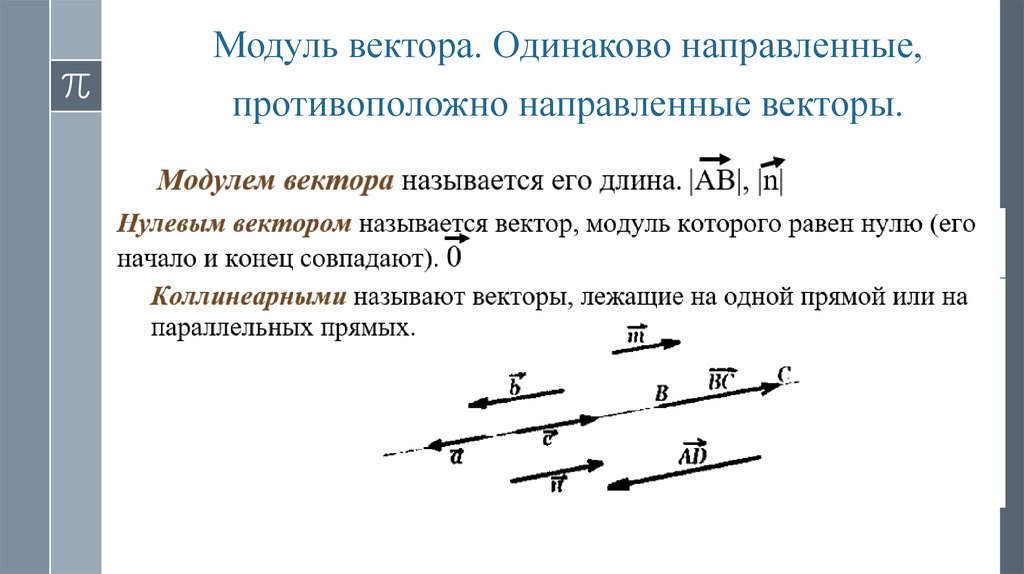
Модуль вектора. Одинаково направленные,
противоположно направленные векторы.

12.

Модуль вектора. Одинаково направленные,
противоположно направленные векторы.

13.

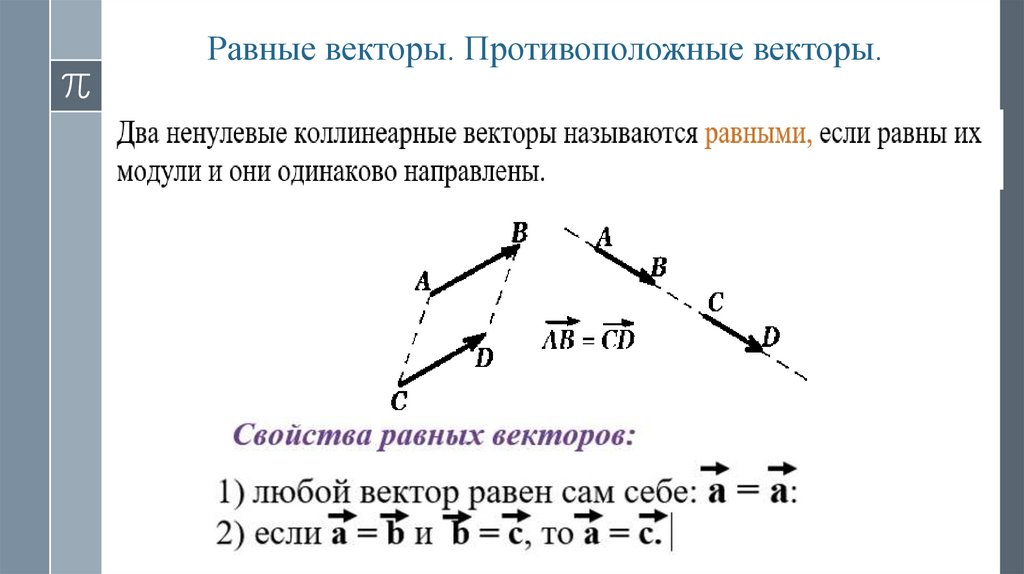
Равные векторы. Противоположные векторы.

14.

Равные векторы. Противоположные векторы.

15.

Вектора в пространстве.

16.

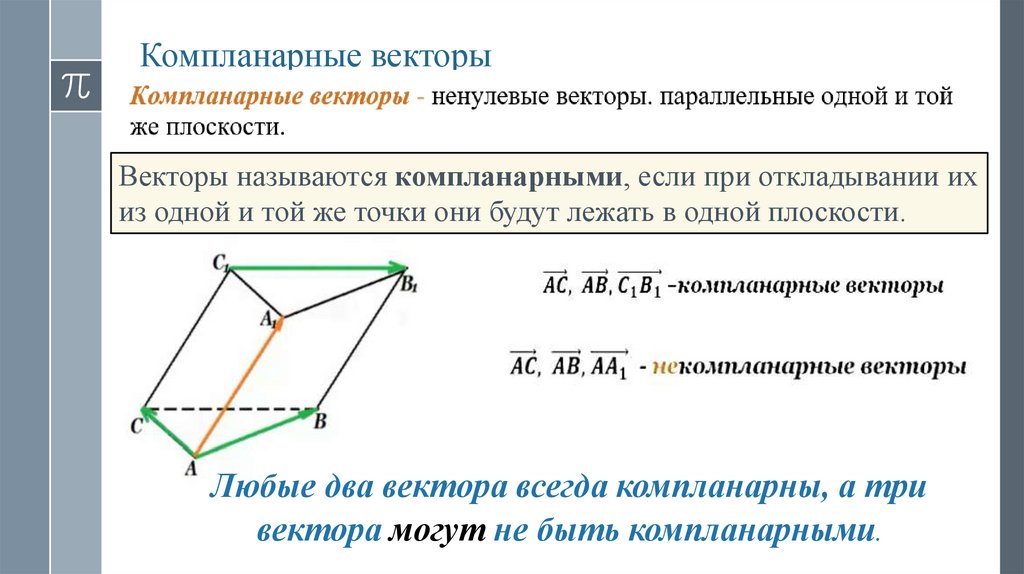
Компланарные векторы
Векторы называются компланарными, если при откладывании их
из одной и той же точки они будут лежать в одной плоскости.
Любые два вектора всегда компланарны, а три
вектора могут не быть компланарными.

17.

Определение
z
1
0
x
1
1
y

18.

z
1
0
x
1
1
y

19.

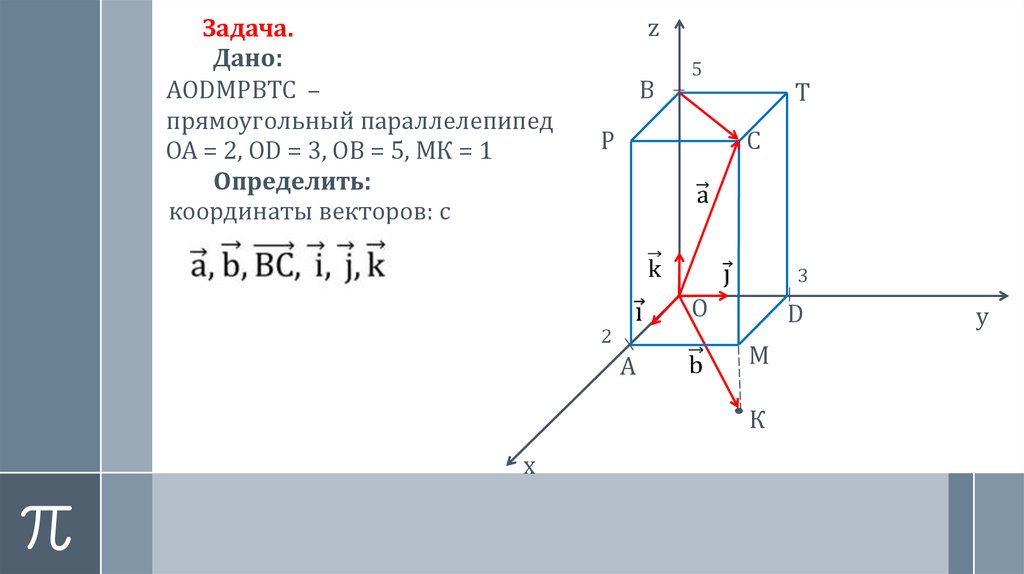
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1
Определить:
координаты векторов: c
z
B
5
P
T
C
3
O
2
A
D
M
К
x
y

20.

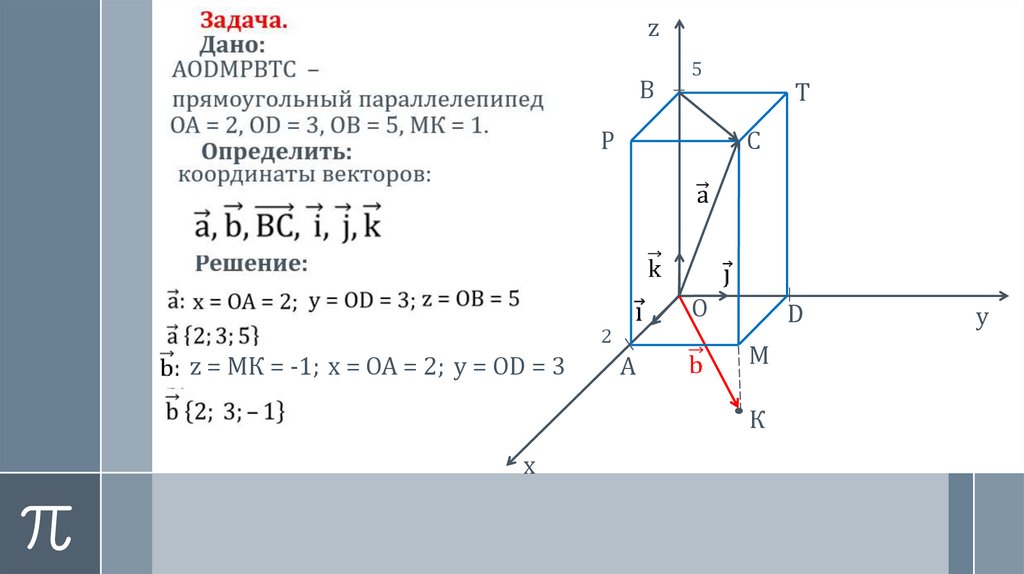
Задача.
Дано:
AODMPBTC –
прямоугольный параллелепипед
ОА = 2, ОD = 3, ОB = 5, МК = 1.
Определить:
координаты векторов:
z
B
5
P
T
C
Решение:
O
2
A
D
M
К
x
y

21.

z
B
5
P
T
C
O
2
z = МК = -1; х = ОА = 2; у = ОD = 3
A
D
M
К
x
y

22.

z
B
5
P
T
C
O
2
A
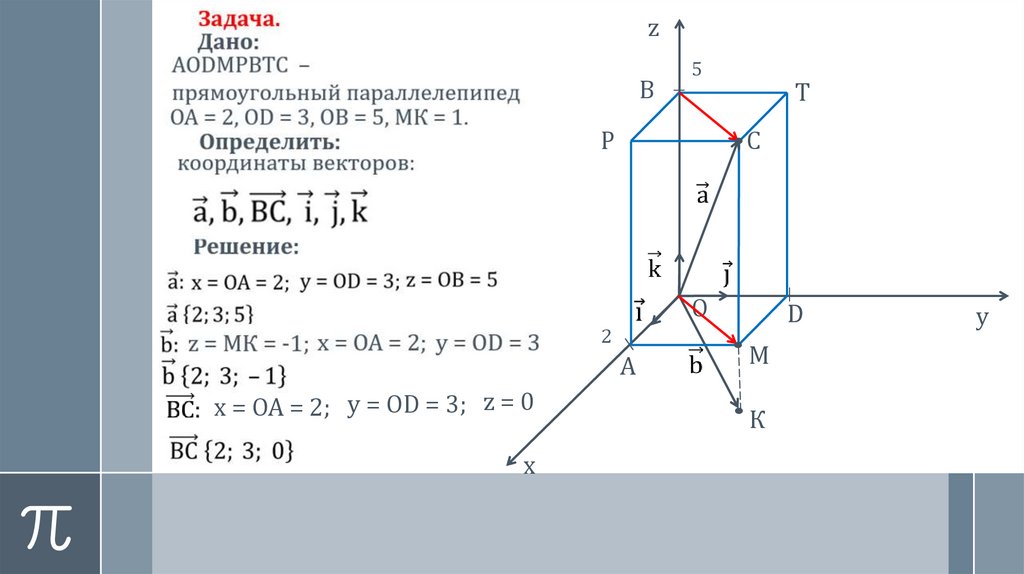
х = ОА = 2; у = ОD = 3; z = 0
x
D
M
К
y

23.

z
B
5
P
T
C
O
2
A
х = ОА = 2; у = ОD = 3; z = 0
x
D
M
К
y

24.

Нулевой вектор
z
y
х

25.

Действия с векторами

26.

СЛОЖЕНИЕ ВЕКТОРОВ
1)Правило треугольника.

27.

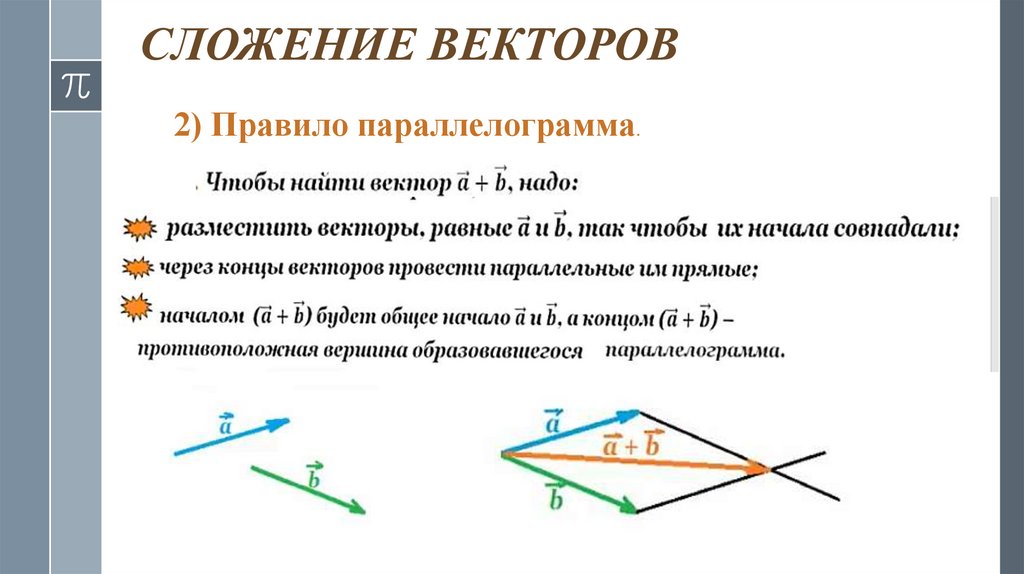
СЛОЖЕНИЕ ВЕКТОРОВ
2) Правило параллелограмма.

28.

СЛОЖЕНИЕ ВЕКТОРОВ
3) Правило многоугольника

29.

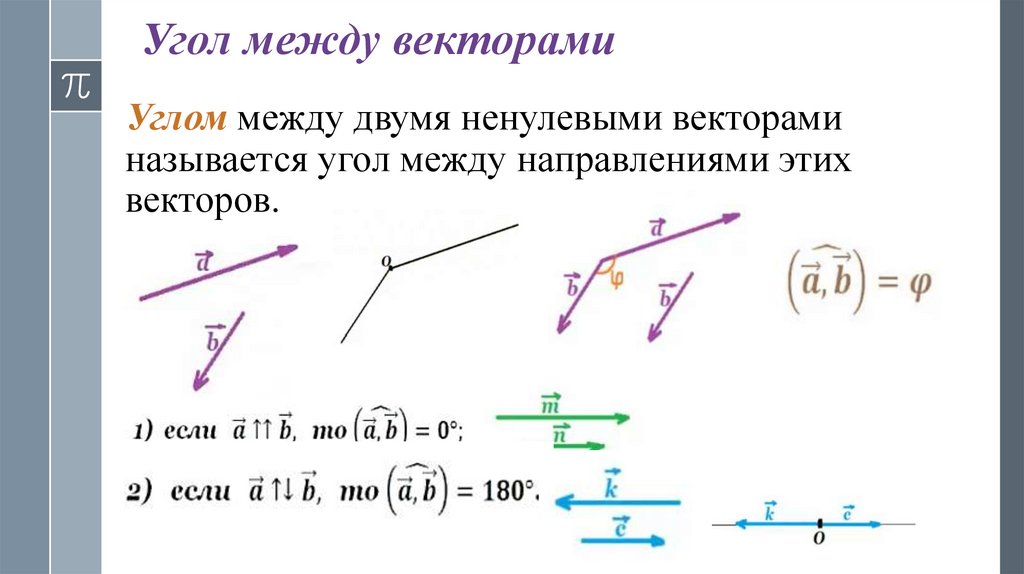
Угол между векторами
Углом между двумя ненулевыми векторами
называется угол между направлениями этих
векторов.

30.

СЛОЖЕНИЕ ВЕКТОРОВ
4) Правило параллелепипеда.
Для сложения трех некомпланарных векторов
применяют правило параллелепипеда.

31.

Связь между координатами
точки и вектора в
пространстве

32.

Два ненулевых вектора называются коллинеарными,
если они лежат на одной прямой или на параллельных
прямых.

33.

Вектор, конец которого совпадает с данной точкой, а
начало – с началом координат, называется радиусвектором данной точки
z
1
радиус-вектор
0
1
x
1
y

34.

Нулевой вектор
z
y
х

35.

Координаты равных векторов
соответственно равны.
х₁ = х₂, у₁ = у₂, z₁ = z₂

36.

Каждая координата суммы двух или более
векторов равна сумме соответствующих
координат этих векторов.

37.

Каждая координата разности двух векторов
равна разности соответствующих
координат этих векторов.

38.

Каждая координата произведения
вектора на число равна произведению
соответствующей координаты вектора на
это число.
данный вектор, α - данное число,

39.

Задача 1.
Дано:
Решение:
1)
2)
Найти:
3)
х = 2 - 0 –2 = 0
у = –4 –1 + 3 = –2
z=0+2+1=3

40.

Задача 2.
Дано:
z
ОА = 4, ОВ = 9, ОС = 2
Найти: координаты
C (0; 0; 2)
Решение:
O
x
A (4; 0; 0)
В y
(0; 9; 0)

41.

Простейшие задачи в
координатах.

42.

1) Длина вектора

43.

2) Расстояние между двумя точками в
пространстве (длина вектора).
Длина вектора AB в пространстве – это расстояние
между точками А и В.

44.

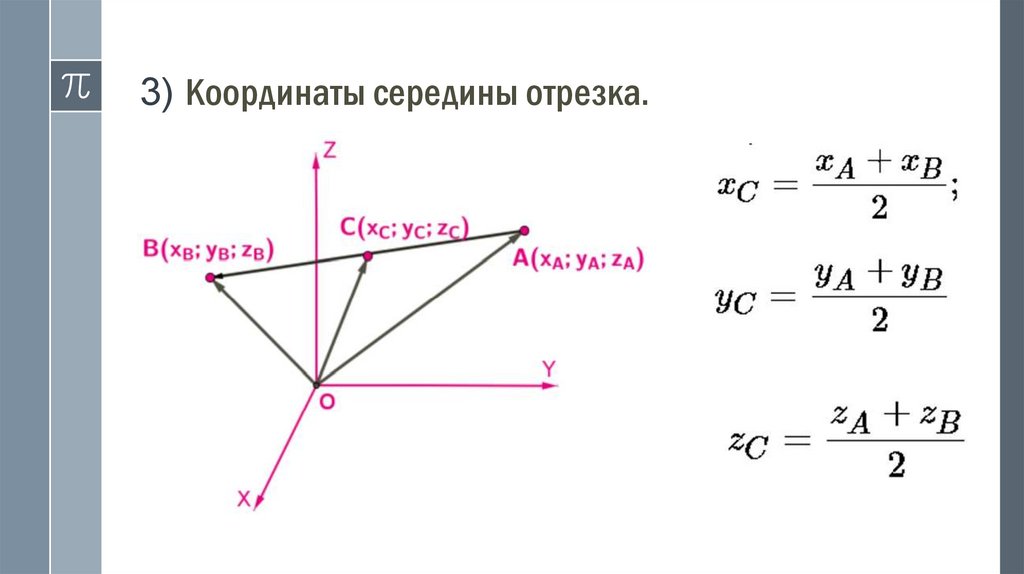
3) Координаты середины отрезка.

45.

4)Скалярное произведение векторов
Скалярным произведением двух векторов называется
число, равное произведению длин этих векторов на
косинус угла между ними.
Скалярное произведение ненулевых векторов равно нулю,
тогда и только тогда, когда эти вектора перпендикулярны.