Similar presentations:
Алгоритмы улучшения качества аудиозаписей
1.
АЛГОРИТМЫ УЛУЧШЕНИЯ КАЧЕСТВААУДИОЗАПИСЕЙ
Коновалов Н.A. ПРИб-221
Научный руководитель: ст. преп. каф. ИСКМ A.C. Астахов
2.
ЦельРеализация и сравнительный анализ методов
спектрального вычитания и Винеровского
оценивания для устранения шумов в
аудиосигналах.
2
3.
Задачи• Рассмотреть основные характеристики
аудиосигналов и особенности их цифрового
представления.
• Описать и реализовать алгоритмы спектрального
вычитания и Винеровского оценивания для
подавления шума.
• Провести сравнительный анализ эффективности
данных методов на искусственном аудиосигнале
при помощи визуализации результатов.
3
4.
Математическая модельЧисленная модель была построена на основе биотеплового
уравнения Пеннеса :
(1)
где
• λ – коэффициент теплопроводности биологической ткани [Вт/(м*К)],
• ρ – плотность биологической ткани [кг/м3],
• с – теплоемкость биологической ткани [Дж/(кг*К)],
• Tb – артериальная температура [K],
• ρb – плотность крови [кг/м3], cb – теплоемкость крови [Дж/(кг*К)], ωb –
перфузия крови [1/c],
• Qmet – объемное внутреннее тепловыделение [Вт/м3].
4
5.
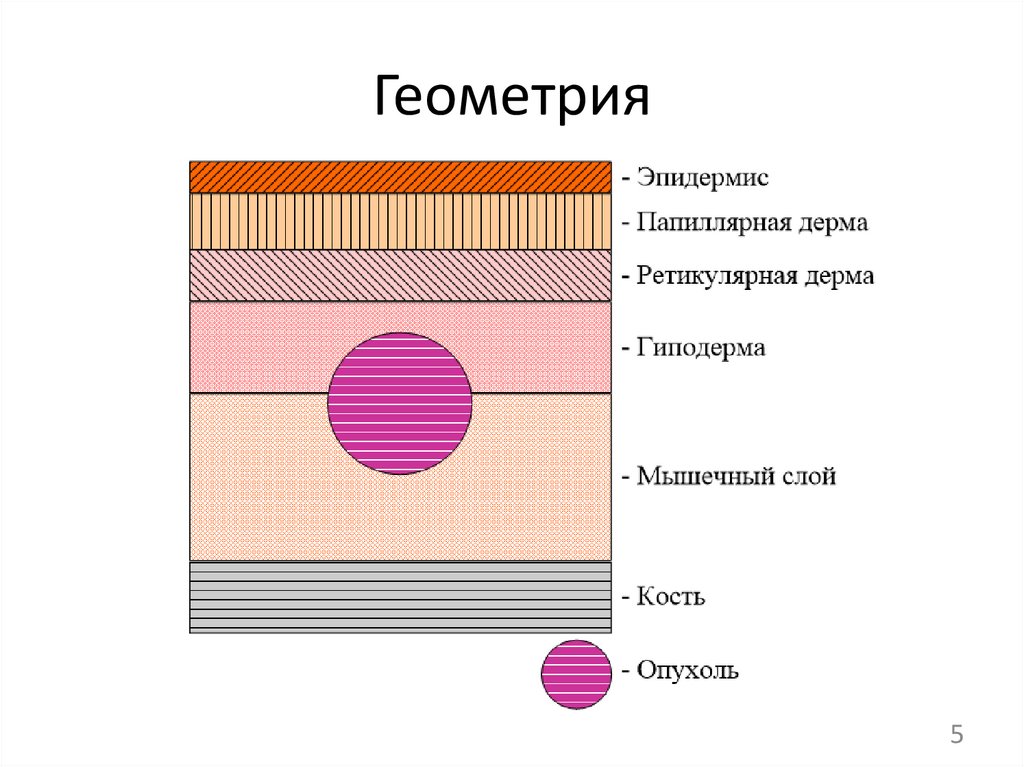
Геометрия5
6.
Физические характеристики биотканейρ[кг/м3]
с [Дж/(Кг * К)]
λ[Вт/(м * К)]
ωb[1/c]
Qmet[Вт/м3]
Эпидермис
1200
3589
0,235
0
0
Папиллярная дерма
1200
3300
0,445
0,0002
368,1
Ретикулярная дерма
1200
3300
0,445
0,0013
368,1
Гиподерма
1000
2674
0,185
0,0001
368,3
Мышечный слой
1085
3800
0,51
0,0027
684,2
Кость
1920
3852
0,44
-
-
Зона опухоли
1030
1440
0,558
0,0063
3700
Кровь
1060
3700
–
–
–
6
7.
Численный методДля численного решения уравнения (1) была выбрана неявная схема Метода
Конечных Разностей (МКР).
Неявная схема является более трудоёмкой, чем явная. Однако неявная схема
абсолютно устойчива.
7
8.
МКРКонечно-разностная аппроксимация биотеплового уравнения (1):
(2)
(3)
Полученная для (2) трёхдиагональная СЛАУ (4) решается методом
прогонки:
(4)
Ход решения для уравнения (3) аналогичен.
8
9.
Тестовая задачаt = 0 c.
t = 400 c.
t = 800 c.
t = 1200 c.
9
10.
Влияние объемного внутреннего тепловыделенияна среднюю температуру биоткани
Однородный квадратный фрагмент биоткани со стороной 10 см.
НУ: 36.6 °С на всем фрагменте биоткани.
ГУ:
1. 1-го рода на границе y = 0 см (T = 37 °С),
2. 2-го рода на границе x = 0 см и x = 10 см
,
3. 3-го рода на границе с окружающей средой y = 10 см (Te = 21 °С).
10
11.
Влияние глубины погружения опухоли радиусом 4мм на температуру слоя кожи, граничащего с
окружающей средой
• Неоднородный квадратный фрагмент кожи со стороной 4 см. Толщина
слоёв биоткани в мм:
Эпидермис
0,2
Папиллярная Ретикулярная
дерма
дерма
0,9
0,9
Гиподерма
Мышечный
Кость
слой
10
20
8
• НУ: 36.6 °С на всем фрагменте биоткани.
• ГУ:
1. 1-го рода на границе y = 0 см (T = 37 °С),
2. 2-го рода на границе x = 0 см и x = 4 см
,
3. 3-го рода на границе с окружающей средой y = 4 см (Te = 21 °С),
4. 4-го рода на границе 2 различных типов биоткани.
11
12.
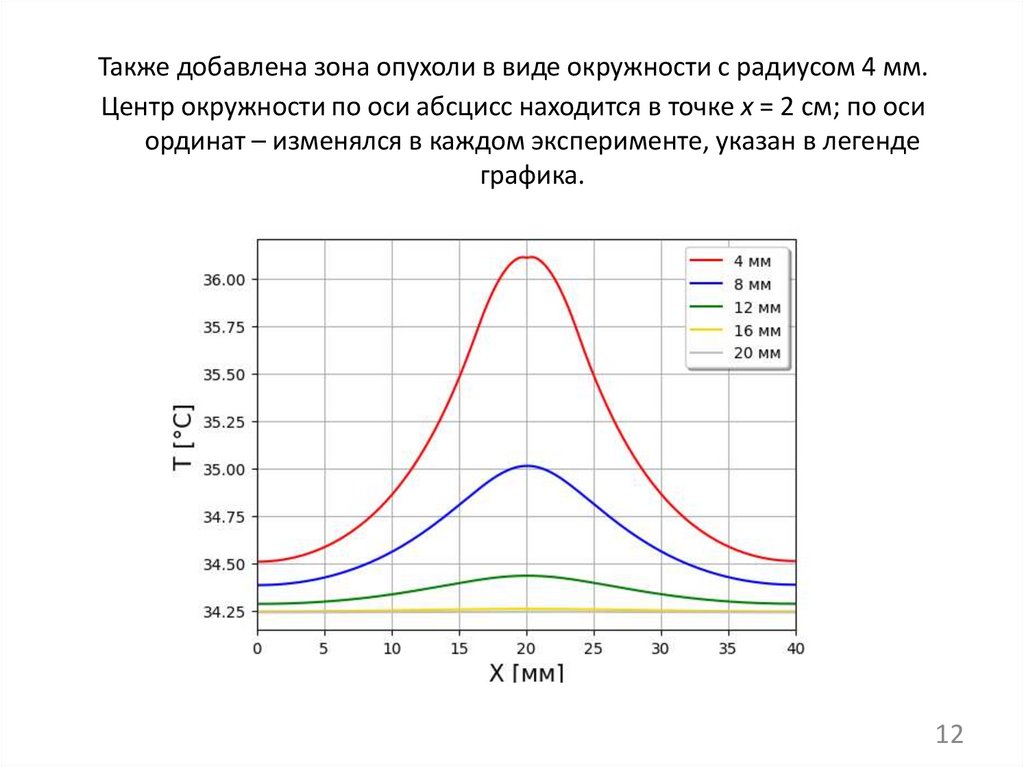
Также добавлена зона опухоли в виде окружности с радиусом 4 мм.Центр окружности по оси абсцисс находится в точке x = 2 см; по оси
ординат – изменялся в каждом эксперименте, указан в легенде
графика.
12
13.
Влияние учёта теплового поля вокруг руки натемпературу слоя кожи, граничащего с окружающей
средой
Условия аналогичны 2 задаче.
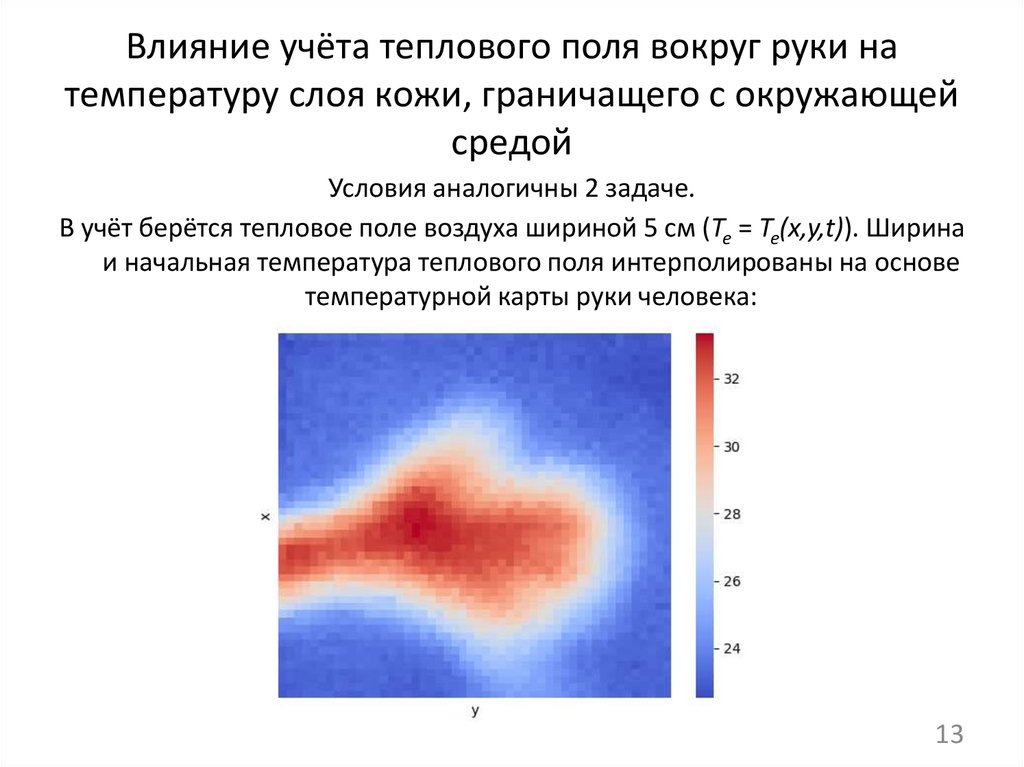
В учёт берётся тепловое поле воздуха шириной 5 см (Te = Te(x,y,t)). Ширина
и начальная температура теплового поля интерполированы на основе
температурной карты руки человека:
13
14.
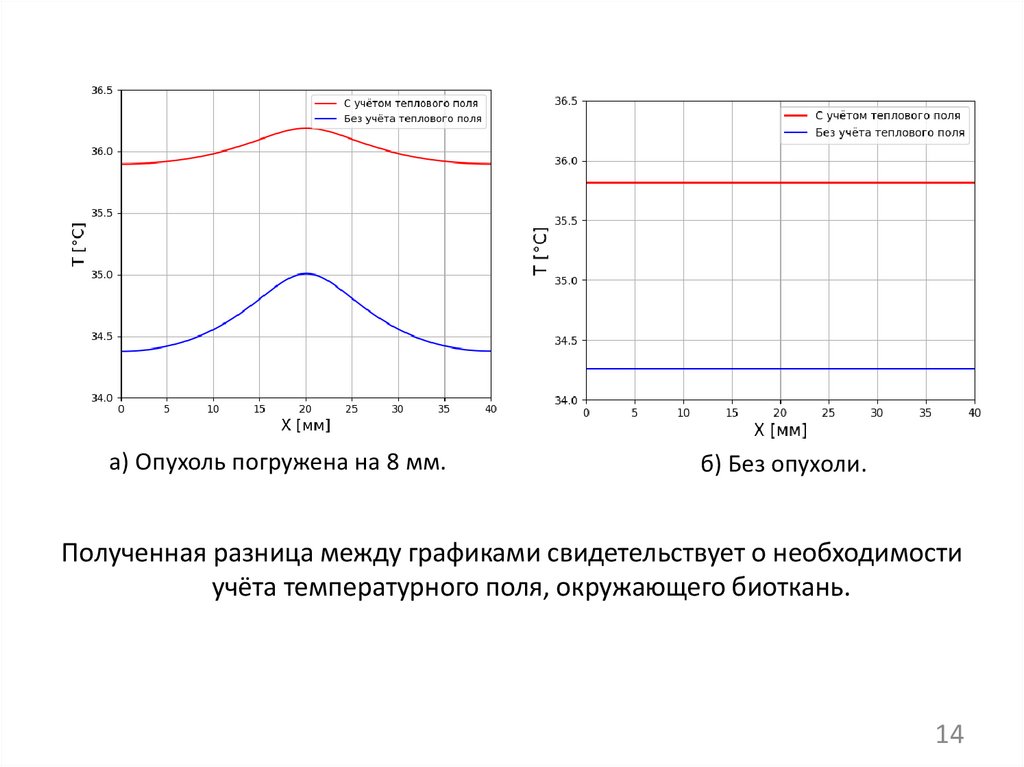
а) Опухоль погружена на 8 мм.б) Без опухоли.
Полученная разница между графиками свидетельствует о необходимости
учёта температурного поля, окружающего биоткань.
14
15.
Заключение• Исследованы зависимости температуры
биоткани от объемного внутреннего
тепловыделения.
• Исследовано влияние опухоли на
температуру внешнего слоя кожи.
• Исследовано влияние теплового поля
вокруг человека на температуру внешнего
слоя кожи.
15











 physics
physics