Similar presentations:
Реальные газы, влажность. Свойства жидкостей (лекция)
1.
Реальные газы, влажность.Свойства жидкостей
2.
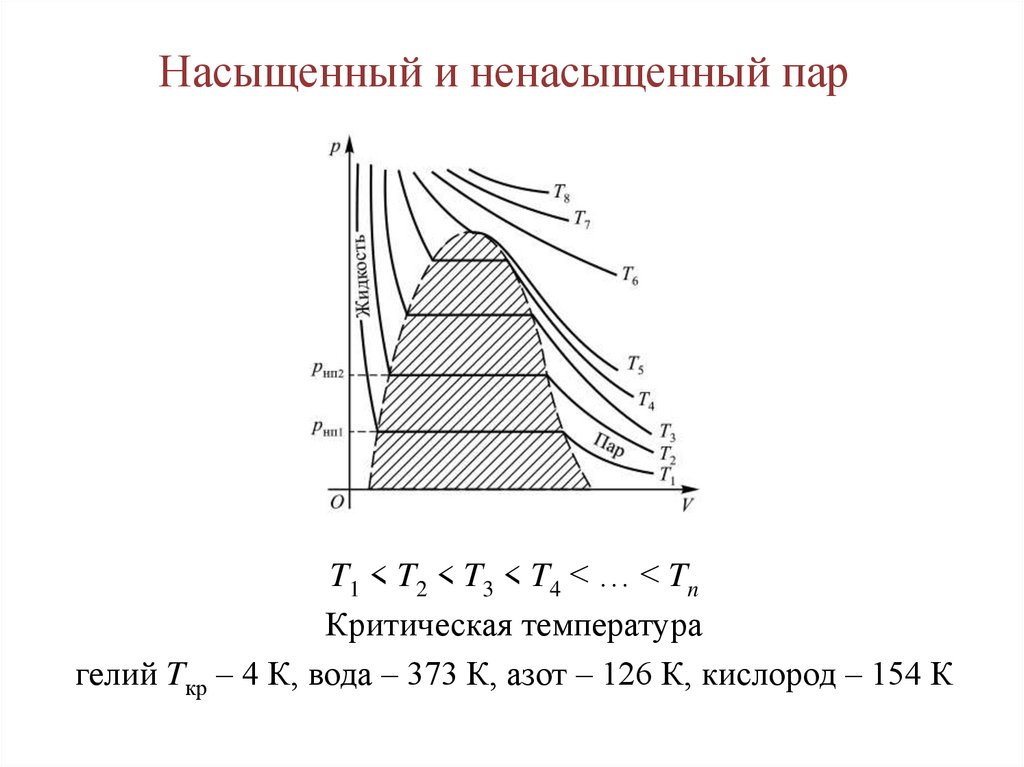
Насыщенный и ненасыщенный парT1 < T2 < T3 < T4 < … < Tn
Критическая температура
гелий Tкр – 4 К, вода – 373 К, азот – 126 К, кислород – 154 К
3.
Реальный газp V b RT
V
p b RT
V
v объем,занимаемый одним молем газа( удельный объем )
RT
RT
p
V
b v b
Cилы взаимодействия молекул
RT
a
p
2
v b v
4.
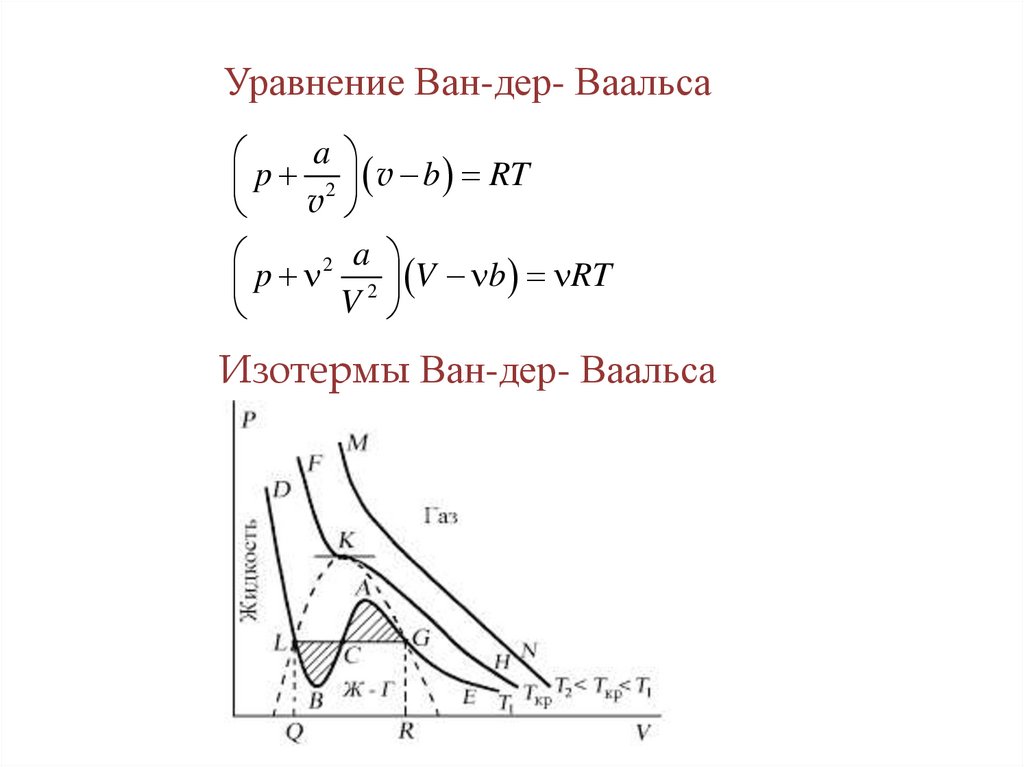
Уравнение Ван-дер- Ваальсаa
p 2 v b RT
v
2 a
p 2 V b RT
V
Изотермы Ван-дер- Ваальса
5.
Внутренняя энергия реального газаadV
a
U 2 const
V
V
a
U CV T
V
6.
Свойства насыщенного пара1. Насыщенный пар находится
в динамическом равновесии с жидкостью.
2. Насыщенный пар не подчиняется газовым законам.
p RT / М
7.
ВлажностьДавление воздуха
ратм = рс.в + рп
рп << рс.в, ратм рс.в
Абсолютная влажность определяется количеством
паров воды в воздухе (плотностью п).
8.
Относительная влажность определяетсяотношением плотности пара к плотности
насыщенного пара нп при той же температуре,
или отношением парциального давления пара
к давлению насыщенного пара рнп при той же
температуре:
pп
ρп
100% =
100%
pн.п
ρ н.п
Единица относительной влажности – процент.
9.
Температура, при которой ненасыщенный парпри данной абсолютной влажности становится
насыщенным, называется точкой росы.
10.
Примеры решения задачРекомендации к решению задач
1) В формулу для определения относительной влажности
входят давление или плотность насыщенного пара, которые
определяем по таблице, если в условии задачи этих данных нет.
2) Для определения массы пара в некотором объеме воздуха
используем определение относительной влажности через
плотность пара.
3) Если известна точка росы tр, то давление пара в воздухе
равно давлению насыщенного пара при tр.
4) При температуре кипения воды 100 С давление насыщенного
пара равно атмосферному давлению.
11.
Задача 1. Определите относительную влажность воздухапри температуре t1 =20 С, если точка росы равна tр = 5 С.
Давление насыщенного пара при температурах t1 и tр,
соответственно равны рнп1 = 2,33 кПа, рнп. р = 0,88 кПа.
Решение.
pнп р / pнп 1 100% 40%
Замечания.
Мы не учли изменение давления при увеличении
температуры, но Т1/Тр = 1,05. Однако в пределах точности
расчета этим отношением можно пренебречь.
12.
Задача 2. Относительная влажность воздуха в помещении60%, а температура 18 С. До какой температуры надо
охладить металлический предмет, чтобы его поверхность
«запотела»?
Решение.
p
100%
pнп
Давление пара при 18 С должно стать равным давлению
насыщенного пара при искомой температуре:
pн.п
p
1, 24 104 Па
100%
рнп 1, 23 104 Па при 10 C
13.
Задача 3. В комнате объемом 40 м3 температура воздуха20 С, его относительная влажность 1 = 20%. Сколько
надо испарить воды, чтобы относительная влажность 2
достигла 50%?
Решение.
m = пV
Mpп
Mpнп φ
pп
п
(
100%)
RT
RT 100%
pнп
Mpнп φ1
Mpнп φ 2
m1
V;
m2
V
RT 100%
RT 100%
MpнпV
m = m2 – m1
φ 2 φ1 0, 21 кг
RT 100%
14.
Задача 4. В комнате при температуре 15 С относительнаявлажность 1 = 10%. Как изменится относительная
влажность, если температура в комнате повысится на 10 С?
Решение.
Влажности воздуха при температурах t1 и t2 равны:
p2
p1
100%
100%; 2
1
pнп2
pнп1
рнп.1 = 1, 71 кПа, рнп2 = 1, 23 кПа
p2
p1
2 1
100%
pн.п2 pн.п1
p1 p2
φ1 pнп1
;
p1
T1 T2
100%
15.
p1T2 φ1 pнп1T2p2 =
T1100%
T1
φ1 pнп1T2
2 =
pнп2T1
pн.п1T2
φ1 pн.п1T2
1 3, 7%
φ1 φ1
Δφ =
pн.п2T1
pн.п2T1
16.
Задача 5. В сосуд объема V = 10-2 м3, наполненный сухимвоздухом при давлении р0 = 105 Па и температуре 0 С,
вводят m = 3 г воды. Сосуд нагревают до 100 С. Каково
давление влажного воздуха в сосуде при этой температуре?
Решение.
р = рв + рп
Предположим, что вся вода испарилась, давление паров
определим из уравнения:
m RT 0, 003 8,31 373
4
рп
Па
=
5,
2
10
Па
2
M V
0, 018 10
По закону Шарля:
p0
105
pв T
373 Па 1,37 105 Па
T0
273
р рв рп р 1,89 105 Па
17.
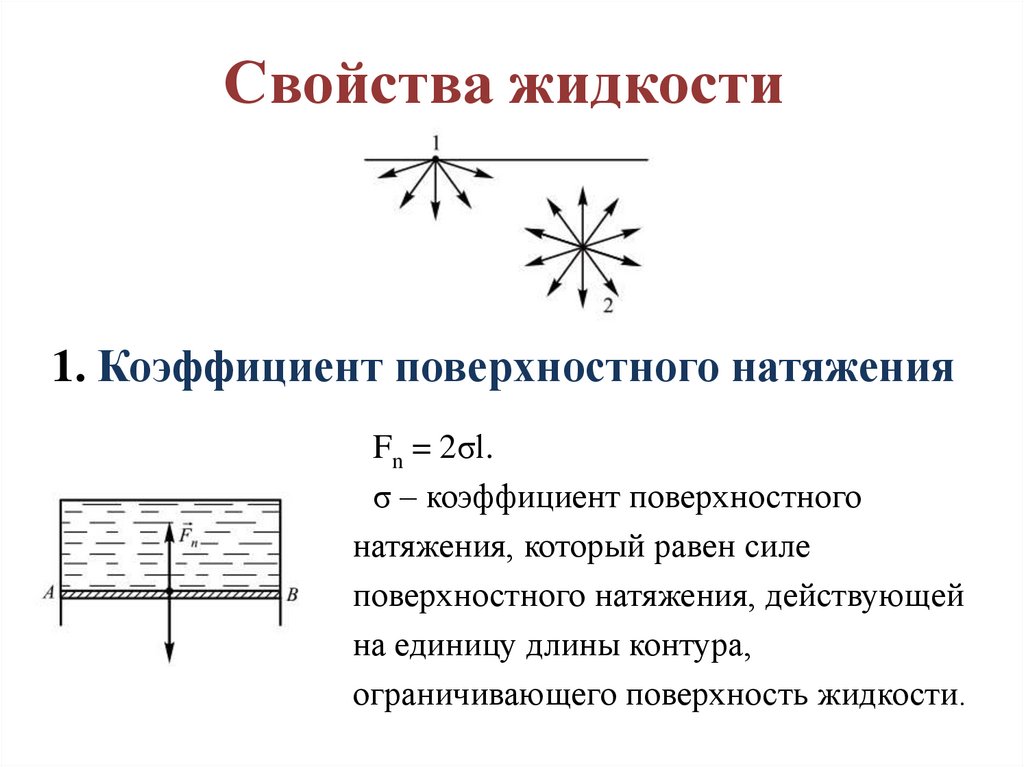
Свойства жидкости1. Коэффициент поверхностного натяжения
Fn = 2σl.
σ – коэффициент поверхностного
натяжения, который равен силе
поверхностного натяжения, действующей
на единицу длины контура,
ограничивающего поверхность жидкости.
18.
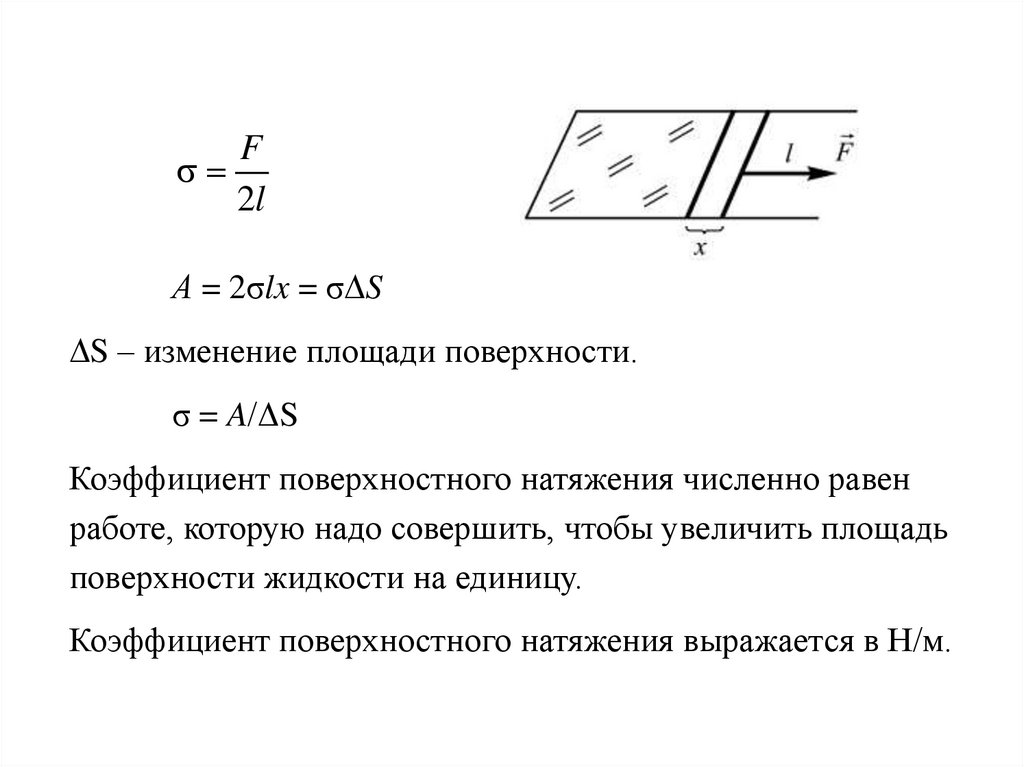
F2l
А = 2σlx = σ S
S – изменение площади поверхности.
σ = A/ΔS
Коэффициент поверхностного натяжения численно равен
работе, которую надо совершить, чтобы увеличить площадь
поверхности жидкости на единицу.
Коэффициент поверхностного натяжения выражается в Н/м.
19.
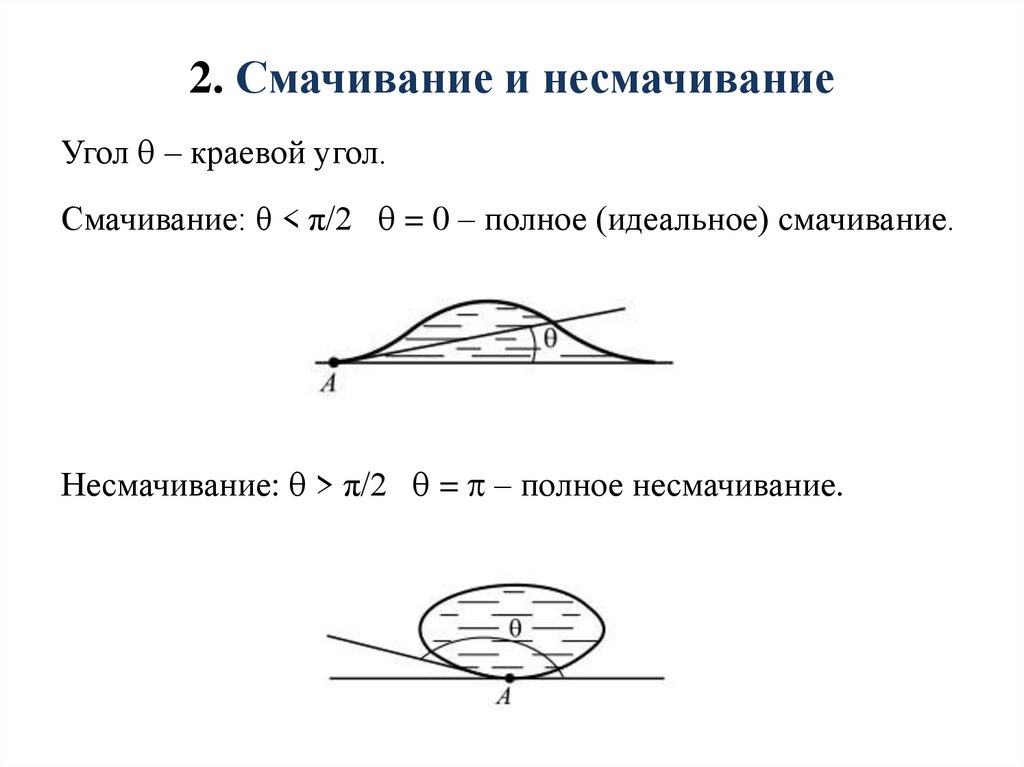
2. Смачивание и несмачиваниеУгол – краевой угол.
Смачивание: θ < π/2 = 0 – полное (идеальное) смачивание.
Несмачивание: > π/2 = – полное несмачивание.
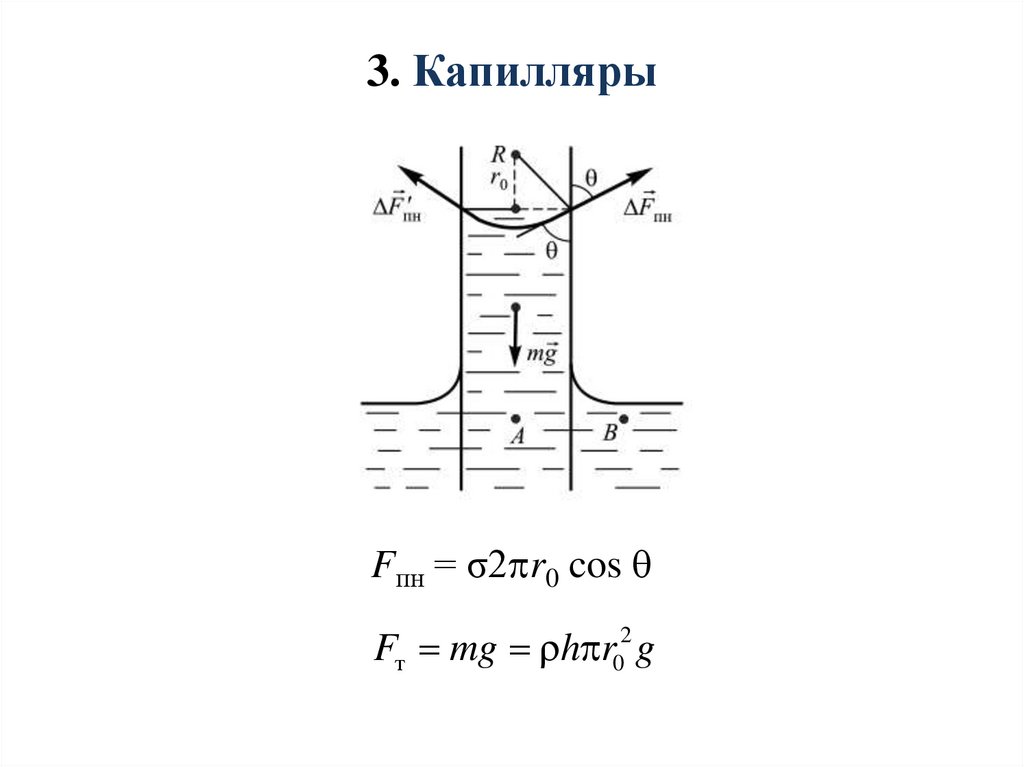
20.
3. КапиллярыFпн = σ2 r0 cos
Fт mg h r02 g
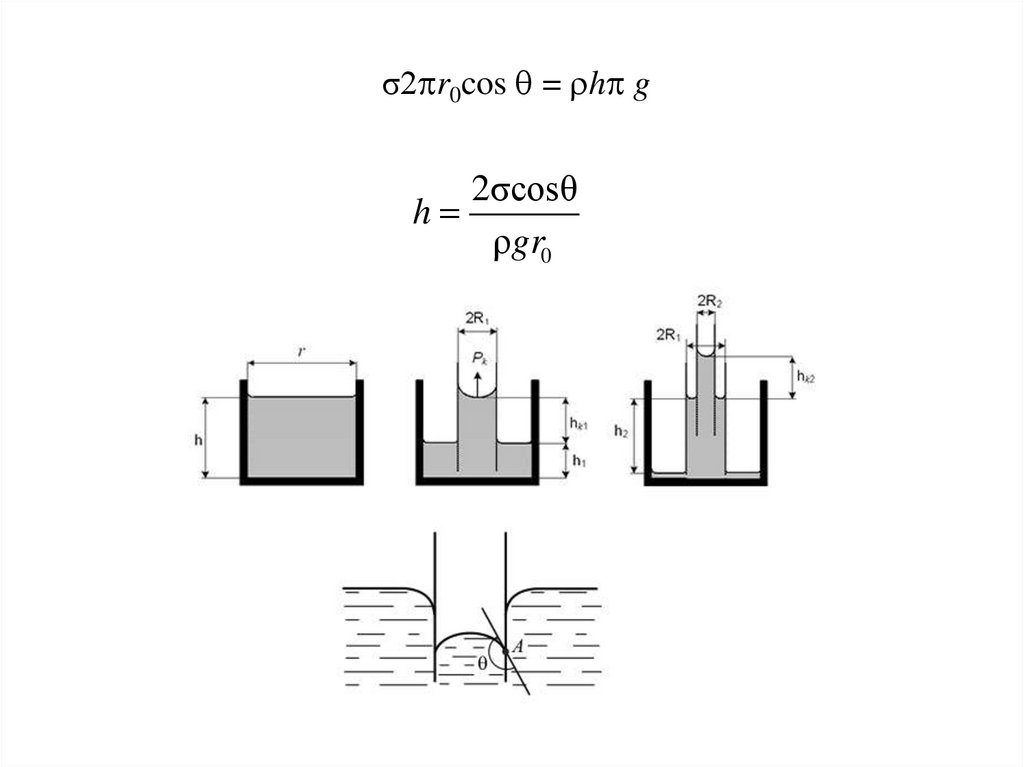
21.
σ2 r0cos = h g2σcosθ
h
ρgr0
22.
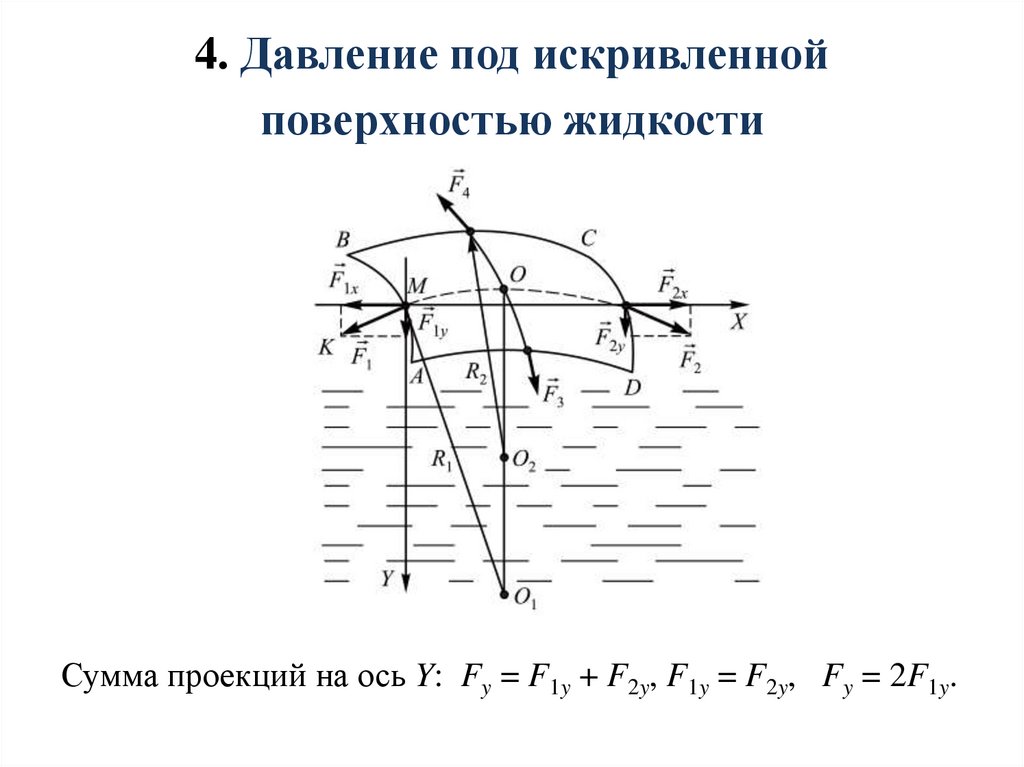
4. Давление под искривленнойповерхностью жидкости
Сумма проекций на ось Y: Fy = F1y + F2y, F1y = F2y, Fy = 2F1y.
23.
МO F1 y, F1y = F1(МO)/R1
R1
F1
F1 = σlAB
Fy = 2 F1y = 2σlAB(МO)/R1= σ S/R1
р1 = σ/R1
р2 = σ/R2
Суммарное добавочное давление равно (формула Лапласа):
1
1
р р1 р2 σ
R1 R2
24.
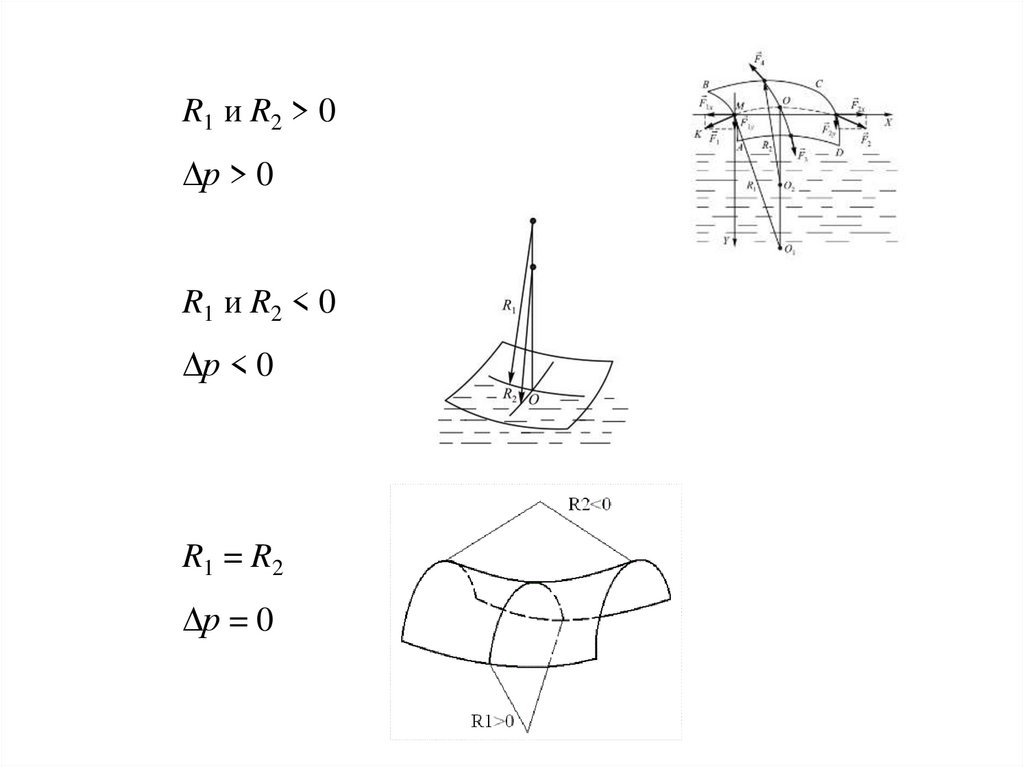
R1 и R2 > 0р > 0
R1 и R2 < 0
р < 0
R1 = R2
р = 0
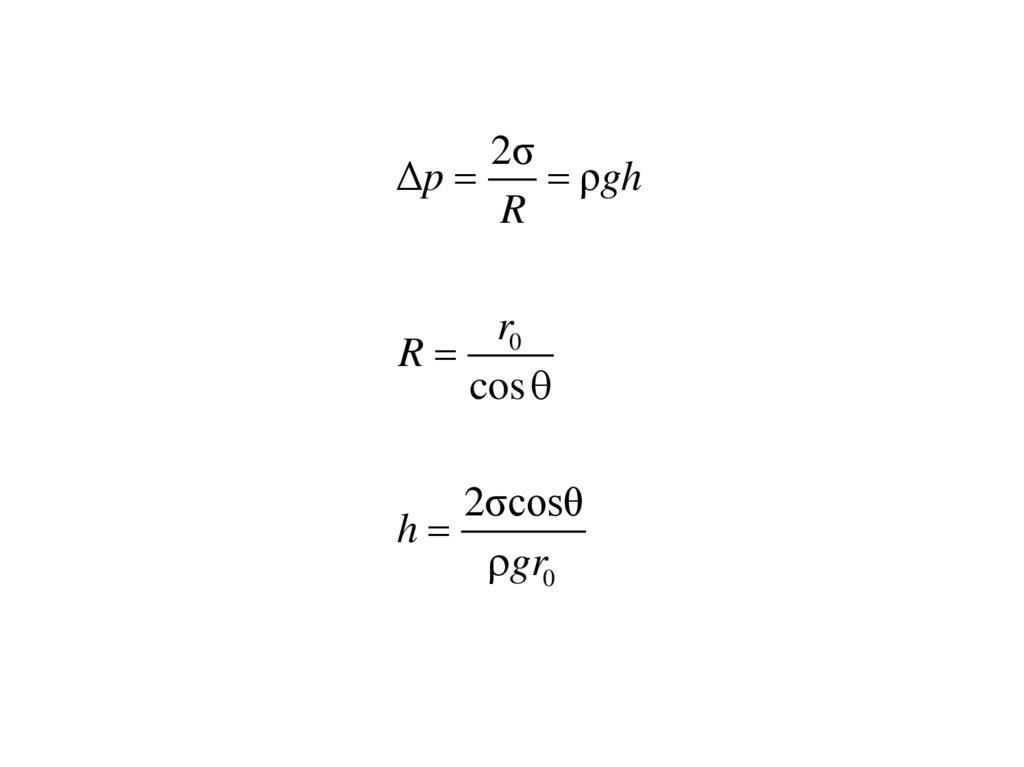
25.
2σΔp
ρgh
R
r0
R
cos
2σcosθ
h
gr0
26.
Примеры решения задачЗадача 1. С какой минимальной высоты должна упасть капля
радиуса R, чтобы она разбилась на n одинаковых маленьких капель?
Коэффициент поверхностного натяжения σ, плотность жидкости .
Температура жидкости не изменяется.
Решение.
S n 4 r 2 – 4 R 2
A 4 r 2 n – R 2
– Eп mgh
m r 4 / 3 R 3
4 / 3 R3 n 4 / 3 r 3 r R / n1/ 3
r 4 / 3 R 3 gh s 4 R 2 ( 3 n – 1)
h
3 3 n 1
Rg
27.
Задача 2. Левое колено U-образной трубки имеет радиус0,5 мм, а правое – 1 мм. Какова разность уровней воды в
этой трубке? Коэффициент поверхностного натяжения
воды равен 0,073 Н/м, краевой угол = 0 .
Решение.
2
p1
cos
r1
p2
2
cos (cos 1)
r2
1 1
g h 2
r1 r2
2 1 1
h
0 ,0146 м
g r1 r2
28.
Задача 3. Определите силу, с помощью которой можно растащитьдва стекла, между которыми попала капля воды массой m.
Расстояние между стеклами d, коэффициент поверхностного
натяжения воды σ, плотность воды .
Вода полностью смачивает поверхность стекол.
Решение.
R1 d / 2 0, R2 0
V
m
R2
m
d
R2 R1
1 1
p 0
R2 R1
F F р S р R22
d 2 m
F
d d
m
29.
Задача 4. В двух длинных открытых с обеих сторон капиллярах,расположенных вертикально, находятся столбики воды длинами 2
и 4 см. Найдите радиусы кривизны нижнего мениска в каждом из
капилляров. Внутренний диаметр капилляра 0,5 мм, смачивание
полное.
Решение.
2
h0
( 0 , cos 1)
gr0
2 0 ,073
м 0, 0298 м
3
3
10 9 ,8 0 ,5 10
h1 h0 h2
h0
F1 F2 mg 0
30.
F1 – mg – F2 0где F1 d 0 ,F2 d 0 cos
d 02
m
h1
4
r0
cos
R1
r0 d 02
F2 d 0
R1
2 R1
d 02 h1
d 02
d 0
d 0 –
g
0 R1
0, 74 мм
gd 0 h1
4
2 R1
2
4
31.
F1 F2 – mg 0d 02
d 02
d 0
h2 g 0
2 R2
4
d 0
R2
0 , 73 мм
gd 0 h2
2
4
32.
Тепловое расширение жидких и твердых телl = l0 (1 + t C),
где l и l0 – размеры тела при температурах t C и 0 С
соответственно, α – коэффициент линейного расширения.
l2 l1( 1 t ),
l1
l1
l0
l2 l0 (1 t2 ) =
(1 t2 )
1 t1
1 t1
1
1 – t1
1 t1
33.
V V0 ( 1 t )V l 3 ( 1 t )
l l0 ( 1 t ) l 3 l03 ( 1 t )3
1 3 t 3( t )2 ( t )3 1 t, 3
m
V
0
m
V0 1 t 1 t
34.
Примеры решения задачЗадача 1. Стержень длиной l10, сделанный из материала с
коэффициентом линейного расширения 1, и стержень длиной l20,
сделанный из материала с коэффициентом линейного расширения
2, спаяли, и получился стержень длиной l10 + l20. Определите
эффективный коэффициент линейного расширения стержня.
Решение.
l1 l10 (1 1t ) ,l2 l20 (1 2t )
l l10 l20 (1 t ) l1 l2
l10 l20 (1 t ) l10 (1 1t ) l20 (1 2t )
1l10 2l20
l10 l20
35.
Задача 2. На сколько изменится вес тела, помещенного в керосин,если керосин нагреть на 50 С? Тело представляет собой медный
шарик радиусом r = 2 см. Коэффициент линейного расширения
меди м = 1,7 10–5 К–1, плотность керосина к = 0,8 103 кг/м3 при
t = 20 C.
Решение.
P Fвыт
Fвыт1 к1V1 g Fвыт 2 к 2V2 g
V1 4 / 3 r 3 ,V2 V1( 1 м t )
м 3 м ,V2 V1 (1 3 м t )
к 2
к1
1 к t
к1
4 3 1 3 м t
P
V1 1 3 м t к1V1 g к1 r
1 g 0, 25 Н
3
1 к t
1 к t
36.
Задача 3. Стальной бензобак автомобиля емкостью V0 = 70 лполностью заполнили бензином при температуре 20 С. После этого
автомобиль оставили на солнце и бак разогрелся до 50 С. Сколько
бензина вытечет из бака? Коэффициент объемного расширения
бензина 1 10–3 К–1, коэффициент линейного расширения стали 1,2
10–5 К–1.
Решение.
Объем бензина при нагревании изменяется по закону V1 = V0(1+ б t).
Изменение объема бензина: V1 = V1 – V0 = V0 б t.
Изменение объема бака: V2 = V2 – V0 = V0 t ст.
Объем вытекшего бензина равен V = V1 – V2 = V0 t( б – ст).
ст = 3 ст = 3,6 10–5 К–1.
V = 7 10–2 30(10–3 – 3,6 10–5) = 2,02 10–3 м3 2 л.
37.
Задача 4. Стальная балка закреплена между двумя стенами притемпературе 10 С. С какой силой концы балки будут давить на стену
при температуре 35 С? Площадь поперечного сечения балки
S = 50 см2. Модуль упругости стали E = 2,1 1011Н/м2.
Решение.
Сила, с которой балка давит на стену, равна F = S, где –
напряжение, возникающее в балке при ее деформации.
l 1
l1 E
l l2 – l1
l2 l1( 1 t )
l l1 t
t / Е E t
F S E S t 3Н
38.
Фазовые превращенияВсе вещества могут существовать в трех агрегатных состояния:
твердом, жидком и газообразном.
Плавление – процесс превращения кристаллического тела в
жидкость. Процесс плавления происходит при постоянной
температуре, при этом поглощается определенное количество
теплоты.
Удельная теплота плавления равна количеству теплоты,
необходимому для того, чтобы расплавить единицу массы
кристаллического вещества, взятого при температуре плавления Tп
Q
Q m
m
Q U
Процесс кристаллизации – это процесс, обратный процессу
плавления.
39.
Испарение – это процесс превращения жидкости в пар.Испарение происходит с поверхности жидкости.
Удельная теплота испарения – количество теплоты, которое
необходимо сообщить жидкости при испарении единицы массы
жидкости для того, чтобы ее температура оставалась постоянной.
Q
m
U Q rисп m
rисп
Конденсация – процесс, обратный процессу испарения.
При этом выделяется теплота.
Количество теплоты, необходимое для превращения единицы
массы жидкости в пар при температуре кипения, называется
удельной теплотой парообразования:
Q
rп Q rп m
m
40.
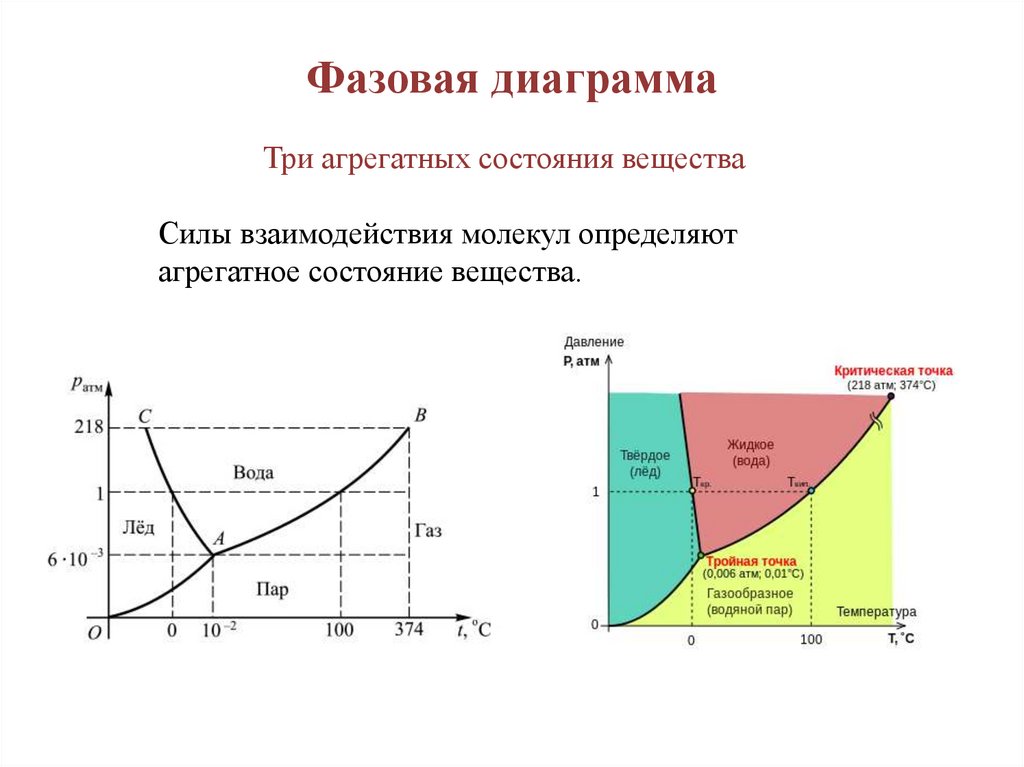
41.
Фазовая диаграммаТри агрегатных состояния вещества
Силы взаимодействия молекул определяют
агрегатное состояние вещества.
42.
Часть кривой АВ показывает зависимость температуры кипенияот давления, при этом жидкость и пар будут в равновесии.
Кривая AC описывает зависимость температуры плавления льда
от давления. При температурах и давлениях, соответствующих
точкам этой кривой, лед и вода будут в равновесии.
Кривая ОА представляет зависимость температуры точек
сублимации от давления (сублимация – процесс, при котором
твердое тело переходит в пар, минуя жидкое состояние).
Точка А – тройная точка, соответствующая тем значениям
температуры и давления, при которых могут одновременно
существовать все три фазы в состоянии равновесия.
43.
Уравнение теплового балансаЕсли система изолирована, то очевидно, что при переходе
в равновесное состояние какие-то части системы отдают
тепло (Q1 < 0), какие-то получают (Q2 > 0). При этом,
поскольку Q = 0 (система изолирована), то
Q1 Q2 0
Qотд Q1 Qпол Q2
Qотд Qпол
44.
Рекомендации к решению задач по теме:Уравнение теплового баланса.
1) Определяем возможные фазовые переходы.
2) Если неизвестно окончательное агрегатное состояние
вещества, то вычисляя Qотд и Qпол и сравнивая значения, делаем
вывод о состоянии системы. Так, если исходные состояния пар
и лед, то при Qпол > Qотд возможное конечное состояние
лед + вода, если Qпол < Qотд, то конечное состояние системы
пар + вода, если Qпол >> Qотд, то в конечном состоянии может
быть только лед и т.д.
3) Составляем уравнение теплового баланса и затем определяем
неизвестную величину.
4) Если при решении получено значение не соответствующее
предполагаемому фазовому состоянию, например, вода при
-20 С, то это означает, что предположение было неверно.
45.
Задача 1. В калориметре находится 1 кг льда при температуре-40 С. В калориметр пускают 1 кг пара при температуре 120 С.
Определите установившуюся температуру и фазовое состояние
системы. Нагреванием калориметра пренебречь.
Решение.
Прежде чем составлять уравнение теплового баланса, Qотд = Qпол,
оценим, какое количество теплоты могут отдать одни элементы
системы, а какое количество теплоты могут получить другие.
Очевидно, что тепло отдают пар при 1) охлаждении до 100 С,
2) при конденсации и вода, сконденсировавшаяся из пара, при
остывании от 100 С. Тепло получают лед при 1) нагревании,
2) при плавлении и вода, полученная из льда, при нагревании
до какой-то температуры.
46.
Оценим количество теплоты, отданное паром при процессах 1 и 2:Qотд = cпm2(t2 – 100 C) + rm2,
Qотд = (2,2 103 1 20 + 2,26 106) Дж = 2,30 106 Дж.
Количество теплоты, получаемое льдом при процессах 1 и 2:
Qпол = cлm1(0 C – t1) + m1,
Qпол = (2,1 103 40 + 3,3 105) Дж = 4,14 105 Дж.
Qотд > Qпол.
Определим, какое количество теплоты нужно дополнительно,
чтобы вода, образовавшаяся из льда, нагрелась до 100 С.
Qпол1 = cвm1(100 – 0 ) = 4,2 103 1 100 Дж = 4,2 105 Дж.
47.
Следовательно, суммарное количество теплоты, которое можетполучить лед в результате процессов 1-3, равно
Qпол
Qпол
8,34 105 Дж
Qотд
Часть оставшегося пара можно определить из соотношения:
mп
Qотд Qпол
rп
0, 65 кг
Температура tx = 100 C,
mп = 0,65 кг, mв = 1,35 кг, mл = 0.
48.
Задача 2. В кастрюлю налили холодной воды с 10 С ипоставили на плиту. Через 10 мин вода закипела. Через какое
время t2 она полностью испарится?
Решение.
Q q 2 rп m
Q1 q 1 св m( tк – t1 )
m
q 1
cв tк t1
q 1
q 2 rп
cв tк t1
2 , 26 106 600
3
2
с
3
,
59
1
0
с 1 ч
3
4 , 2 10 90
49.
Задача 3. Под колоколом воздушного насоса находится вода,масса которой 40 г, а температура 0 С. Воздух из-под колокола
быстро откачивается. Благодаря интенсивному испарению части
воды (насос откачивает пар), остальная вода замерзает.
Определить массу образовавшегося льда, если его температура
также t = 0 C, r = 2,26 106 Дж/кг, = 3,3 105 Дж/кг.
Решение.
Qпол rmп , Qотд mл
Qпол Qотд
rmп mл
m mп mл
mп ( / r )mл
mл ( 1 / r ) m
mл m / ( 1 / r ) 0,035 кг
50.
Задача 4. На электрической плитке мощности 1 кВт кипит водав чайнике. Найдите скорость истечения пара из носика чайника
V, если считать пар идеальным газом. Давление пара p на конце
носика 1 атм, сечение носика 1 см2. Считать, что вся энергия
плитки передается воде.
Решение.
Q mr
Nt
m
r
р 1 атм ( t C 100 C )
m
RT vtS
V
Mp
NRT
NtRT
mRT
7 ,5 м / с
v=
MpSt rMpSt rMpS



















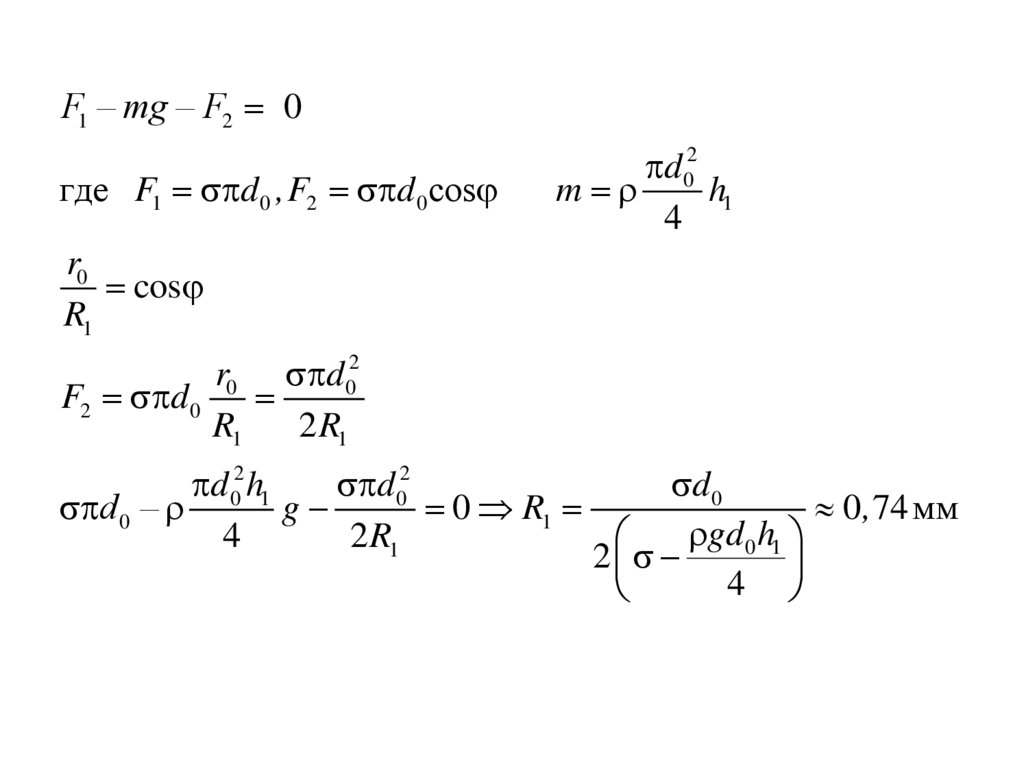
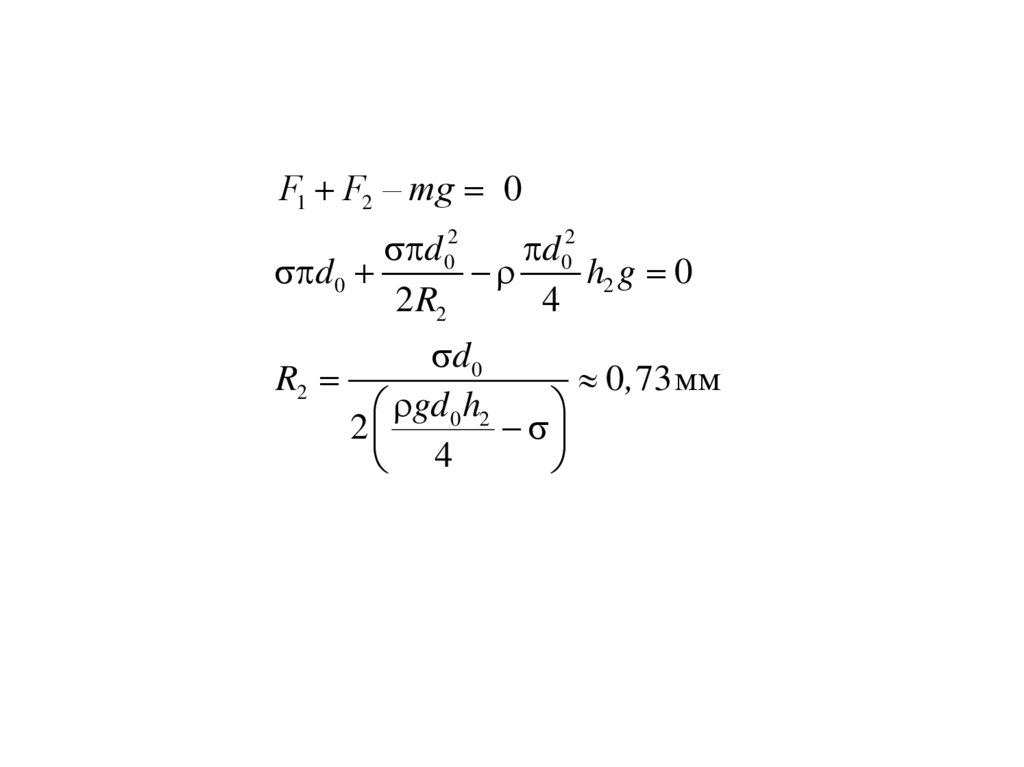

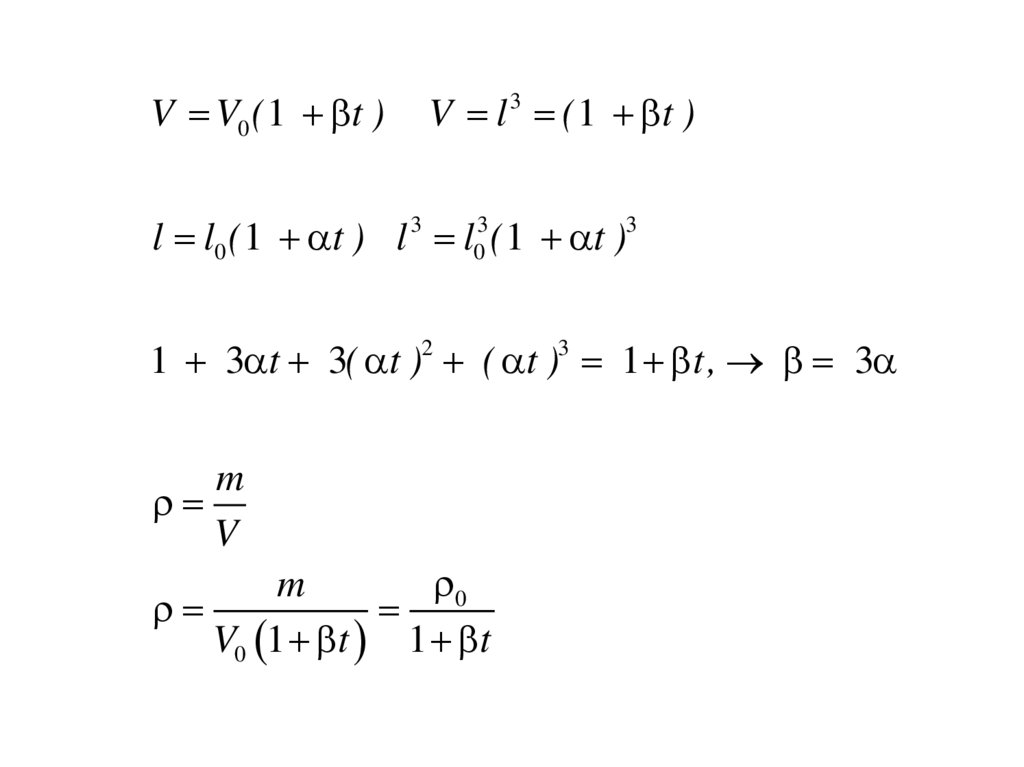
















 physics
physics








