Основные физические свойства жидкостей и газов. Параметры, определяющие свойства жидкостей и газов

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра водопользования и экологии
Механика жидкости и газа
Тема 1
Основные физические свойства
жидкостей и газов. Параметры,
определяющие свойства жидкостей
и газов. Силы
Федоров Святослав Викторович
к.т.н., доцент, доцент

2.

ОПРЕДЕЛЕНИЕ ЖИДКОСТИ
2
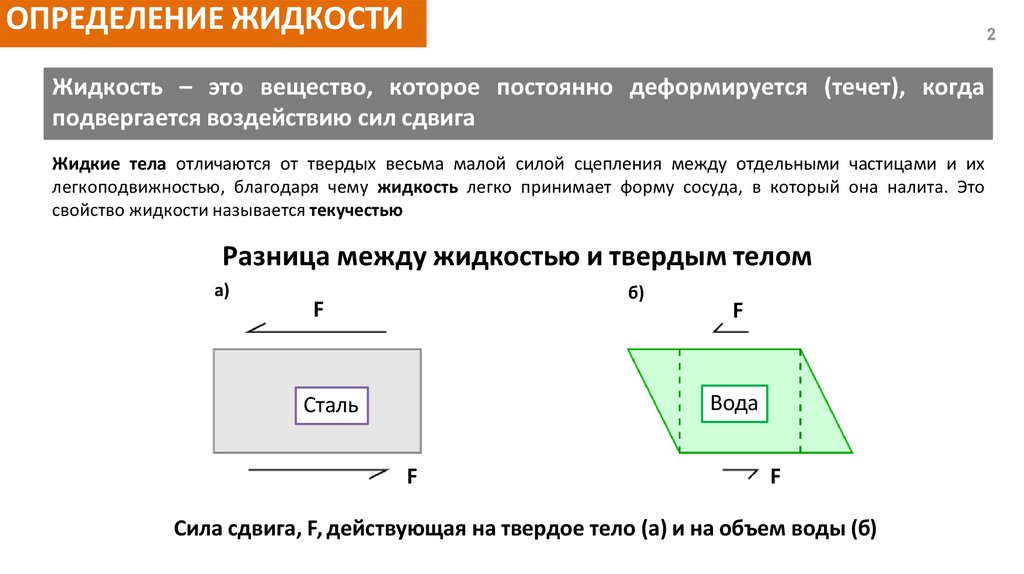
Жидкость – это вещество, которое постоянно деформируется (течет), когда
подвергается воздействию сил сдвига
Жидкие тела отличаются от твердых весьма малой силой сцепления между отдельными частицами и их
легкоподвижностью, благодаря чему жидкость легко принимает форму сосуда, в который она налита. Это
свойство жидкости называется текучестью
Разница между жидкостью и твердым телом
а)
б)
F
F
Вода
Сталь
F
F
Сила сдвига, F, действующая на твердое тело (а) и на объем воды (б)

3.

ОСНОВНЫЕ ФИЗИЧЕСКИЕ СВОЙСТВА ЖИДКОСТЕЙ И ГАЗОВ
Жидкость
Капельная жидкость
Газы
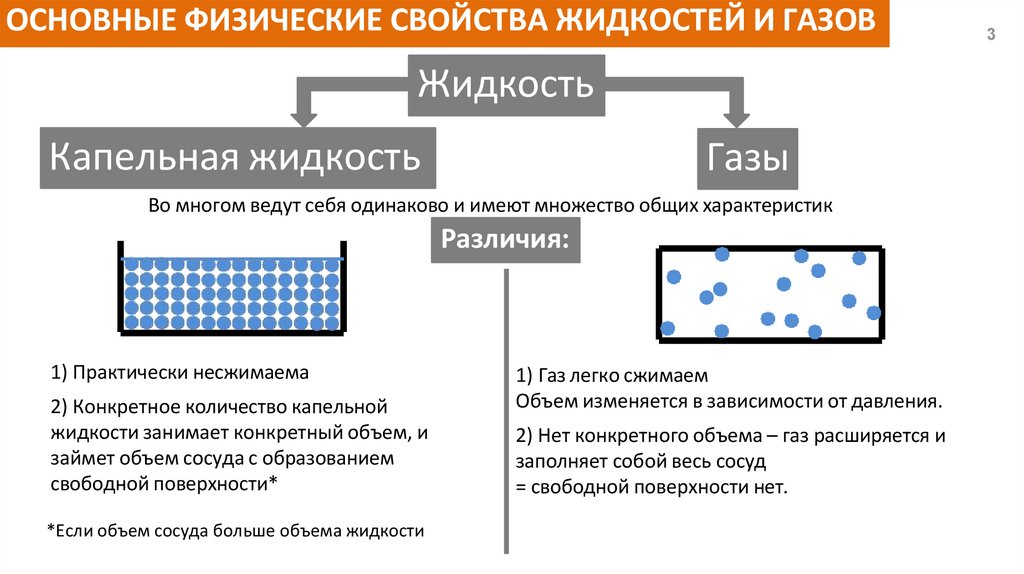
Во многом ведут себя одинаково и имеют множество общих характеристик
Различия:
1) Практически несжимаема
2) Конкретное количество капельной
жидкости занимает конкретный объем, и
займет объем сосуда с образованием
свободной поверхности*
*Если объем сосуда больше объема жидкости
1) Газ легко сжимаем
Объем изменяется в зависимости от давления.
2) Нет конкретного объема – газ расширяется и
заполняет собой весь сосуд
= свободной поверхности нет.
3

4.

ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ СВОЙСТВА ЖИДКОСТИ
1) вязкость
4
τ=max
Касательные
напряжения
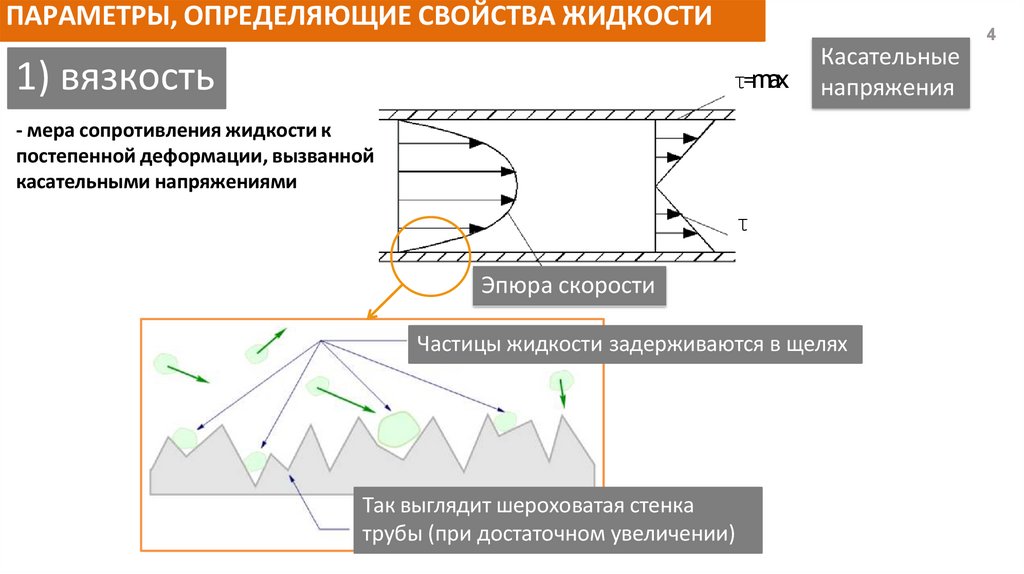
- мера сопротивления жидкости к
постепенной деформации, вызванной
касательными напряжениями
τ
Эпюра скорости
Частицы жидкости задерживаются в щелях
Так выглядит шероховатая стенка
трубы (при достаточном увеличении)

5.

ВЛИЯНИЕ ВЯЗКОСТИ НА ПРОЦЕСС ТЕЧЕНИЯ ЖИДКОСТИ
5
Моделирование движения жидкостей с
различной вязкостью. Жидкость слева обладает
меньшей вязкостью, нежели жидкость справа
НАПРИМЕР:
Вода
И
Клей

6.

ЗАКОН ВЯЗКОСТИ
6
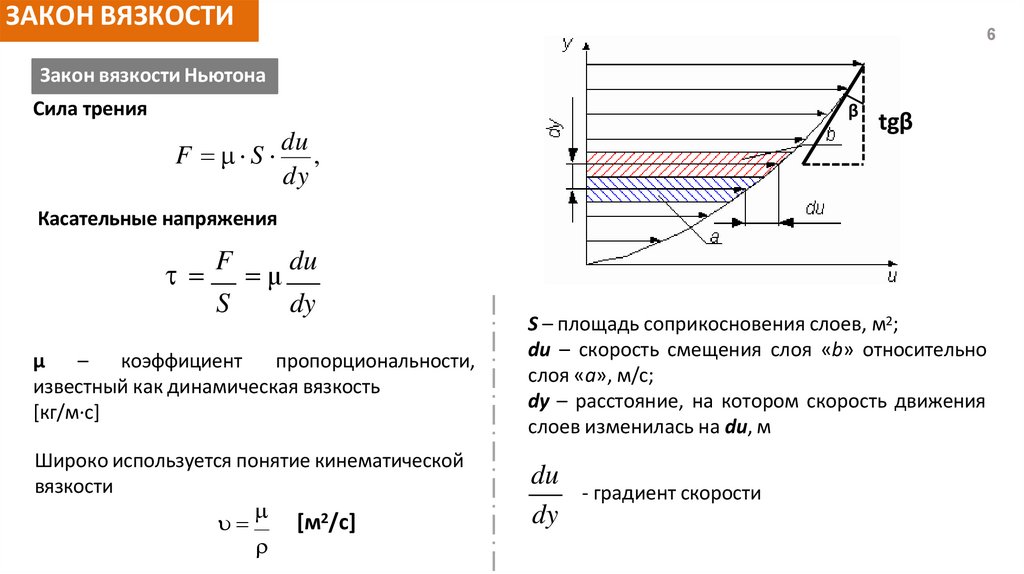
Закон вязкости Ньютона
Сила трения
β
F S
du
,
dy
tgβ
Касательные напряжения
F μ du
S
dy
μ
–
коэффициент
пропорциональности,
известный как динамическая вязкость
[кг/м∙с]
Широко используется понятие кинематической
вязкости
[м2/с]
S – площадь соприкосновения слоев, м2;
du – скорость смещения слоя «b» относительно
слоя «a», м/с;
dy – расстояние, на котором скорость движения
слоев изменилась на du, м
du
dy
- градиент скорости

7.

ВЯЗКОСТЬ ЖИДКОСТИ И ГАЗОВ
7
ЖИДКОСТЬ
ГАЗ
μ1
μ1
T, °С ↑
T, °С ↑
μ2
μ2
μ1 > μ2
μ1 < μ2

8.

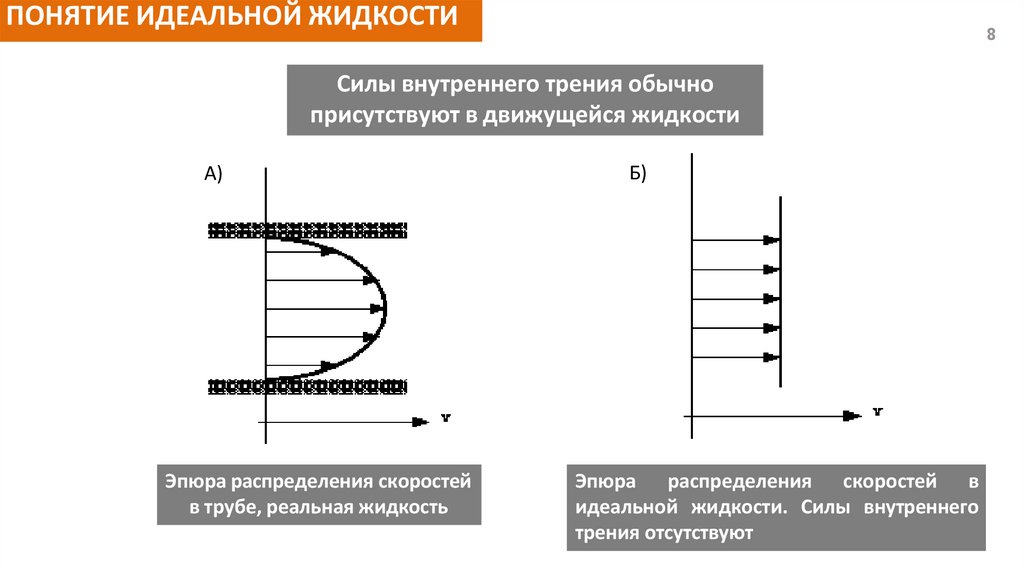
ПОНЯТИЕ ИДЕАЛЬНОЙ ЖИДКОСТИ
8
Силы внутреннего трения обычно
присутствуют в движущейся жидкости
A)
Эпюра распределения скоростей
в трубе, реальная жидкость
Б)
Эпюра распределения скоростей в
идеальной жидкости. Силы внутреннего
трения отсутствуют

9.

τ, касательные напряжения
НЬЮТОНОВСКИЕ И НЕНЬЮТОНОВСКИЕ ЖИДКОСТИ
Бингамовская
Ньютоновская
9
Выражение для определения
величины
касательных
напряжений:
du
K
dy
Дилатантная
Псевдопластичная
n
Коэффициент n –
характеризует степень
неньютоновского поведения.
du/dy, скорость сдвига
Жидкости, подчиняющиеся закону
Ньютона, для которых динамическая
вязкость µ постоянна, называются
Ньютоновскими жидкостями.
Коэффициент K – зависит от
консистенции жидкости и
увеличивается с ростом вязкости.
Жидкости, для которых
динамическая вязкость µ не
постоянна, называются
Неньютоновскими жидкостями.

10.

КЛАССИФИКАЦИЯ НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ
10
НЕНЬЮТОНОВСКИХ ЖИДКОСТЕЙ
ХАРАКТЕРИСТИКИ НЕ ЗАВИСЯТ ОТ
ВРЕМЕНИ
ХАРАКТЕРИСТИКИ ЗАВИСЯТ ОТ
ВРЕМЕНИ
Бингамовская
ТИКСОТРОПНЫЕ
μ
T
Псевдопластичная
РЕОПЕКТИЧЕСКИЕ
μ
БИНГАМОВСКАЯ
ПСЕВДОПЛАСТИЧНАЯ
T
Дилатантная
ДИЛАТАНТНАЯ

11.

ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ СВОЙСТВА ЖИДКОСТИ
11
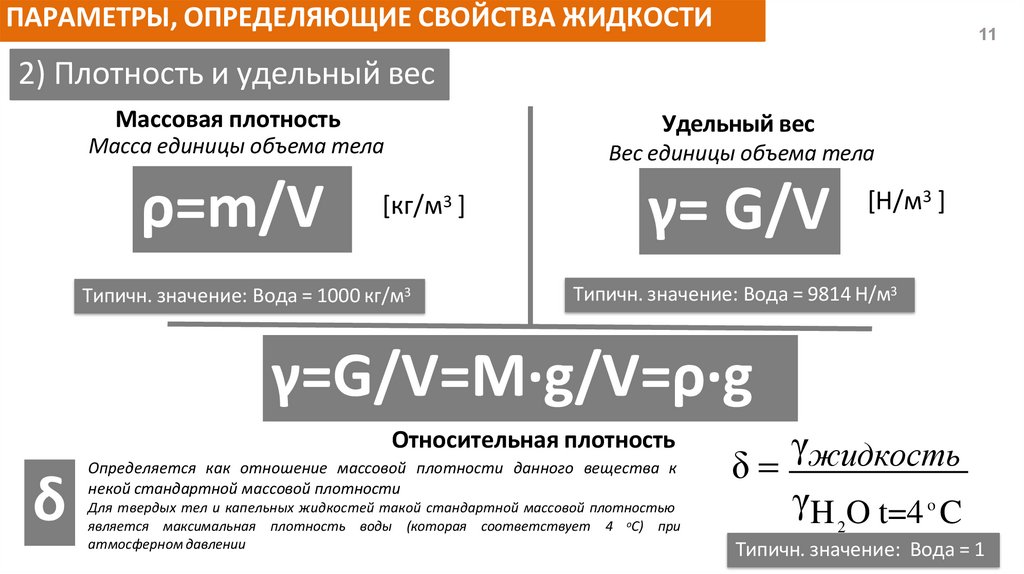
2) Плотность и удельный вес
Массовая плотность
Удельный вес
Масса единицы объема тела
Вес единицы объема тела
ρ=m/V
γ= G/V
[кг/м3 ]
Типичн. значение: Вода = 1000 кг/м3
[Н/м3 ]
Типичн. значение: Вода = 9814 Н/м3
γ=G/V=M∙g/V=ρ∙g
Относительная плотность
δ
Определяется как отношение массовой плотности данного вещества к
некой стандартной массовой плотности
Для твердых тел и капельных жидкостей такой стандартной массовой плотностью
является максимальная плотность воды (которая соответствует 4 оС) при
атмосферном давлении
γжидкость
δ
γH O t=4 o C
2
Типичн. значение: Вода = 1

12.

ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ СВОЙСТВА ЖИДКОСТИ
3) Сжимаемость
Капельные жидкости
характеризуются очень
маленькой сжимаемостью
F
это свойство жидкости уменьшать свой объем под
действием внешних сил
Коэффициент объемного сжатия
- относительное изменение объема жидкости при
изменении давления на единицу
dW
W
W1
12
1 dW [1/Па]
в
W dP
dW W1 W
W1 W 1 βв dP
Величина, обратная коэффициенту объемного сжатия представляет собой
объемный модуль упругости (модуль Юнга) Е [Па]: Е = 1/βв
dW
dP
W
E
обобщенный закон Гука
Для воды при нормальных условиях:
βв=0,5∙10-9 Па-1; Е=2∙109 Па

13.

ПРИМЕР ЗАДАЧИ
p
dW
W
13
В баке под давлением P = 200 000 Па находится 2 м3 воды. Как
изменится объем воды, если давление на поверхности жидкости
увеличить до 1 000 000 Па?
Решение
dP = 1 000 000 – 200 000 = 800 000 = 0,8*106 Па
W1 W 1 βв dP
W1 2 1 0,5 10 9 0,8 106 1,9992м3

14.

ПАРАМЕТРЫ, ОПРЕДЕЛЯЮЩИЕ СВОЙСТВА ЖИДКОСТИ
4) Температурное расширение
F
dW
W
W1
14
Коэффициент температурного расширения
- это относительное изменение объема
жидкости при изменении температуры на 1 К
при постоянном давлении:
1 dW
βt
dW W1 W
[1/К]
W dT
W1 W 1 βt dT
Температура воды, °C
Коэффициент объемного
теплового расширения, К-1
5-10
0,53∙10-4
10-20
1,50∙10-4
20-40
3,02∙10-4
40-60
4,58∙10-4
60-80
5,87∙10-4

15.

ПРИМЕР ЗАДАЧИ
15
Температурное расширение в системе отопления
ияв дслиясткеомэефф
мвниодго
ППрриимреарвнивйаоябвъыермаж
воедны
отиоцпилееннтиаяоибнъдеи
уаслжьантоигяо идотеммаптеерпалтоувронйогмоощностью
штисроеснтиавялчяеерте4з5d0Wл, получим следующую зависи мость:
3р0аксВ
Вычислим увеличение объема воды при на гр ева ниис в5 до 80 °C
dP
dT
t
Wсжатия
βt в гидравлических
dT
Для диапазона 1–25 бар коэффициентdW
объемного
расчетах
принимают равным:
- 9 КП
оэа
ф-ф1ициент
=0,5∙10
β
Температура
Увеличение
в
Температура
dT
температурного
Выполняе м равсочд
етыы, °вCтабл ице:воды, К
объема, л
расширения, К- 1
Коэффициент
Температура
Увеличение
5 температурного
0,53∙10-4
0,119
278,15-28 3,15 dT
5-10
воды, °C
давления, МПа
1,50∙10
0,675
283,15-29 3,15
10 расширения,
К-1 -4
10-20
20-40
293,15-313,15 5
5-10
20
-4
-4
3,02∙10
0,53∙10
0,53 2,718
40-60
313,15-333,15 10
10-20
20
-4
-4
4,58∙10
1,50∙10
3,0 4,122
60-80
333,15-353,15 20
20-40
20
-4
-4
5,87∙10
3,02∙10
12,1 5,283
4,58∙10-4
12,917 (2,8 7% )
18,32
60-80
5,87∙10-4
23,48
Чтобы принять до полнительный
систему отопления
о бъем 20
жидкости, образующийся
при ее нагревании,
40-60
20
оснащают мембранным расширительным баком
Итого:
Итого:
57,43

16.

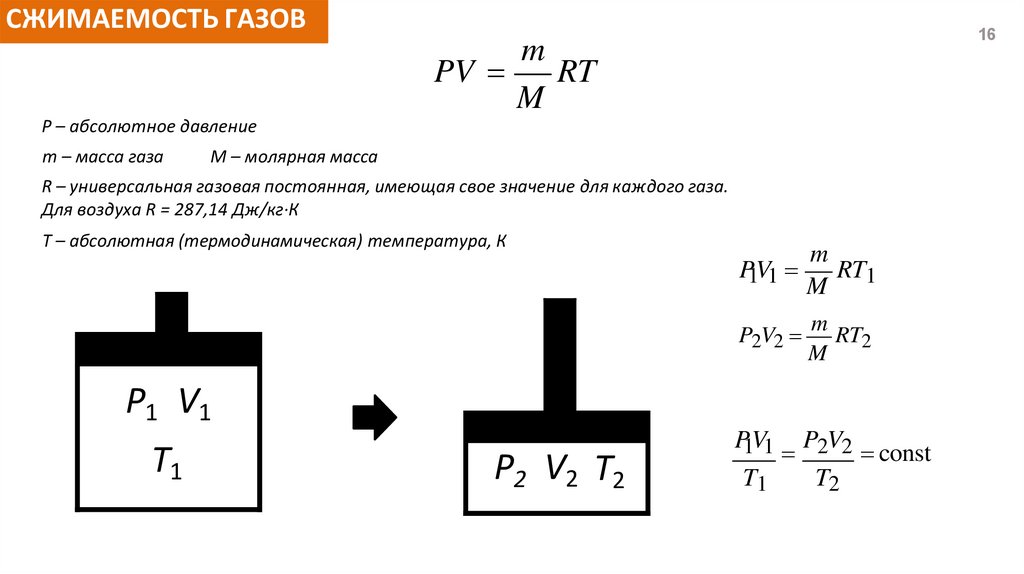
СЖИМАЕМОСТЬ ГАЗОВ
16
m
RT
PV
M
P – абсолютное давление
m – масса газа
M – молярная масса
R – универсальная газовая постоянная, имеющая свое значение для каждого газа.
Для воздуха R = 287,14 Дж/кг∙К
T – абсолютная (термодинамическая) температура, К
m
P1V1
RT1
M
P2V2
m
RT2
M
P1 V1
T1
P2 V2 T2
P1V1
PV
2 2 const
T1
T2

17.

ИЗОПРОЦЕССЫ
17
Процесс, при котором один из макроскопических параметров данного газа некоторой массы
остается неизменным, называют изопроцессом
T = const
P = const
V = const

18.

Сжимаемость газов. Изотермический процесс
Изотермический процесс — процесс изменения состояния данного г аза некоторой массы, протекающий при
неизменной температуре.
293 К
293 К
P1 V1
T
Па
P1V1 P2V2
T
T
P2 V2 T
Па
P1V1 P2V2
или
Восходящее движение пузырька воздуха в
жидкости в состоянии покоя
1 – пузырек на дне канала (начало подъема);
2- пузырек на поверхности воды (конец
подъема).
Закон Бойля — Мариотта
m
RT
PV const
M
18

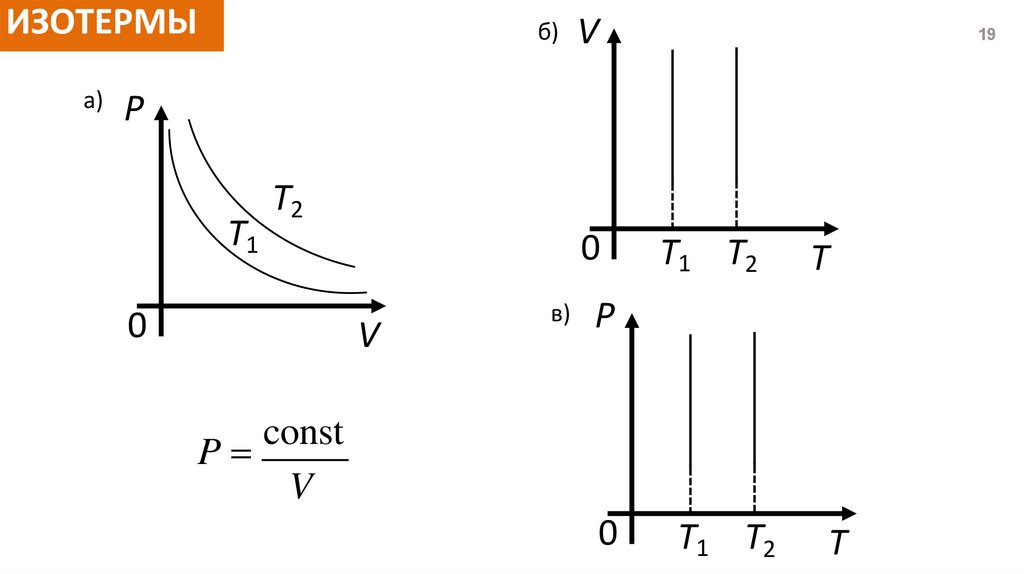
19.

ИЗОТЕРМЫ
а)
б)
V
19
P
T1
T2
0
0
V
в)
T1 T2
T
T1 T2
T
P
const
P
V
0

20.

Сжимаемость газов. Изобарный процесс
20
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при
неизменном давлении.
Pатм
250 К
500 К
Pатм
P V2
Па
T2
P V1 T1
Па
Закон Гей-Люссака
PV1 PV2
T1
T2
V1 V2
T1 T2
или
V
m R
const
T
M P

21.

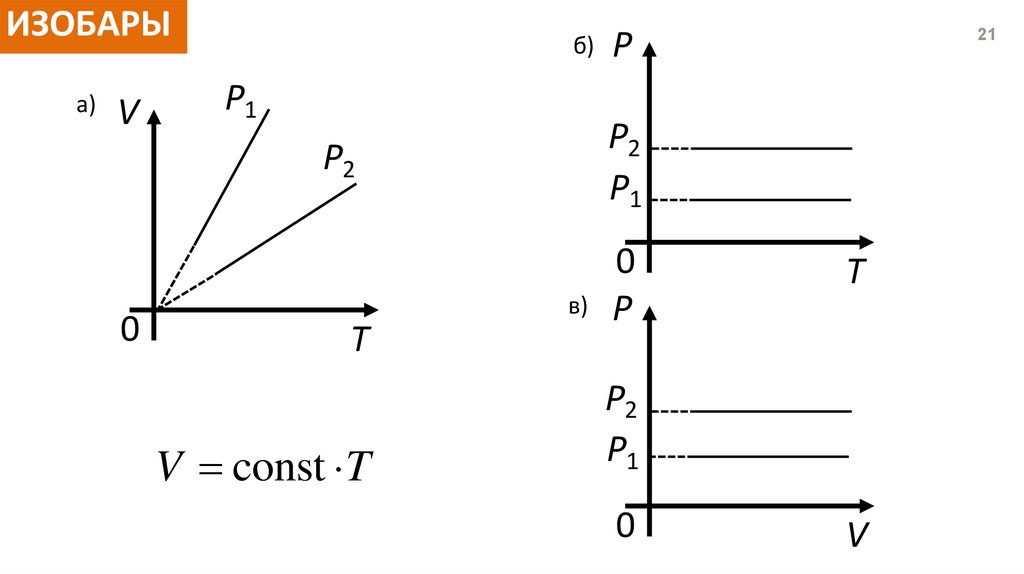
ИЗОБАРЫ
а)
V
б)
P1
P2
0
T
V const T
P
21
P2
P1
0
в) P
T
P2
P1
0
V

22.

Сжимаемость газов. Изохорный процесс
22
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при
неизменном объеме.
250 К
250 К
P2 V
P1 V
Па
T2
T1
Па
Закон Шарля
P1V P2V
T1
T2
P1 P2
T1 T2
или
P
m R
const
T
MV

23.

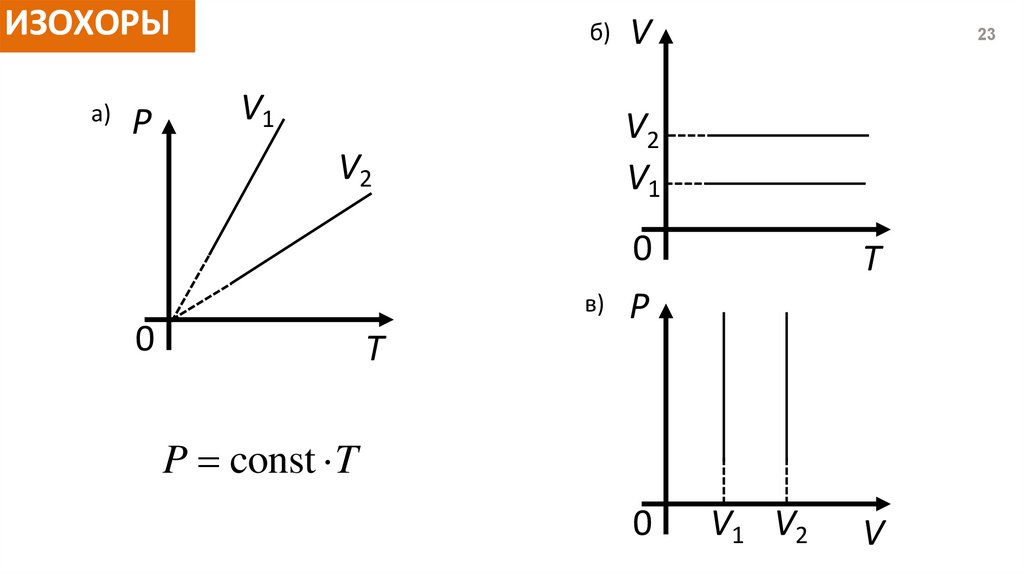
ИЗОХОРЫ
а)
P
б)
V1
V
23
V2
V1
V2
0
в)
0
T
P
T
P const T
0
V1 V2
V

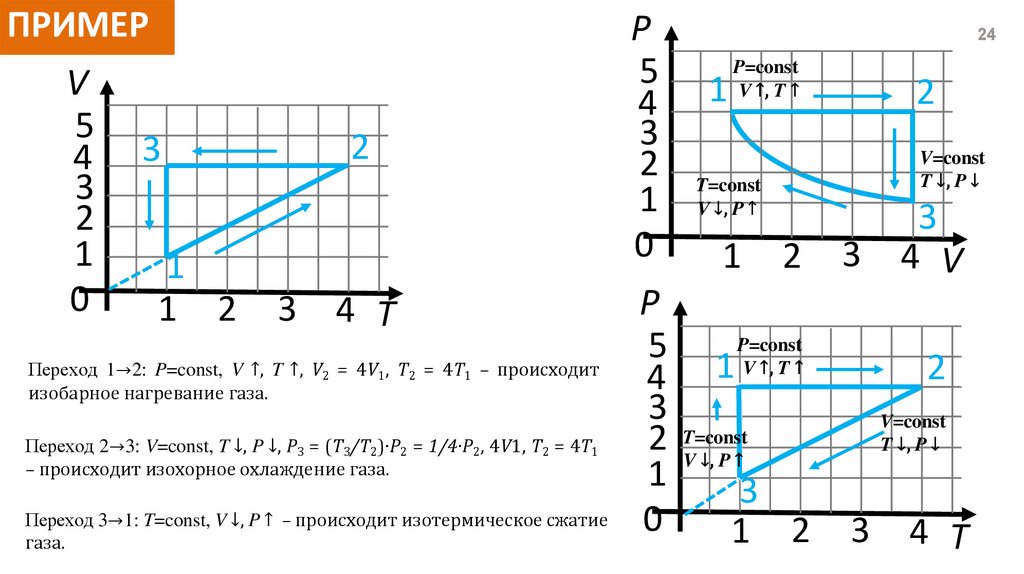
24.

ПРИМЕР
V
5
4 3
3
2
1
1
0
1 2
2
3
4 T
Переход 1→2: P=const, V ↑, T ↑, V2 = 4V1, T2 = 4T1 – происходит
изобарное нагревание газа.
Переход 2→3: V=const, T ↓, P ↓, P3 = (T3/T2)∙P2 = 1/4∙P2, 4V1, T2 = 4T1
– происходит изохорное охлаждение газа.
Переход 3→1: T=const, V ↓, P ↑ – происходит изотермическое сжатие
газа.
P
5
4
3
2
1
0
24
1
P=const
V ↑, T ↑
2
V=const
T ↓, P ↓
T=const
V ↓, P ↑
1
2
P
P=const
5
V ↑, T ↑
1
4
3
2 T=const
V ↓, P ↑
1
3
0
1 2
3
3
4 V
2
V=const
T ↓, P ↓
3
4 T

25.

ПРИМЕР
25
V1 = 5 л
V1 = 2 л
P1 - ?
P2
ΔP = -15 кПа
P1V1 P2V2
P1V1 P1 P V2
P2 P1 P
P V2 1,5 104 5 10 3
25кПа
P1
V1 V2 2 10 3 5 10 3

26.

Сжимаемость газов. Адиабатный процесс
В переменных P, V:
P
k
PV const
T1
26
k
или
P2 V1
P1 V2
В переменных T, V:
Равновесный процесс, в котором к термодинамической системе не подводится от окружающей
k 1 среды и
T2 V1
не отводится в окружающую
2 среду тепло, называетсяkа д1иабатным.
T
TV
В переменных P, T:
Работа газа
0
const
или
V
1 k
TP k const
или
T1 V
1 k
P1 k
T2
T1 P2

27.

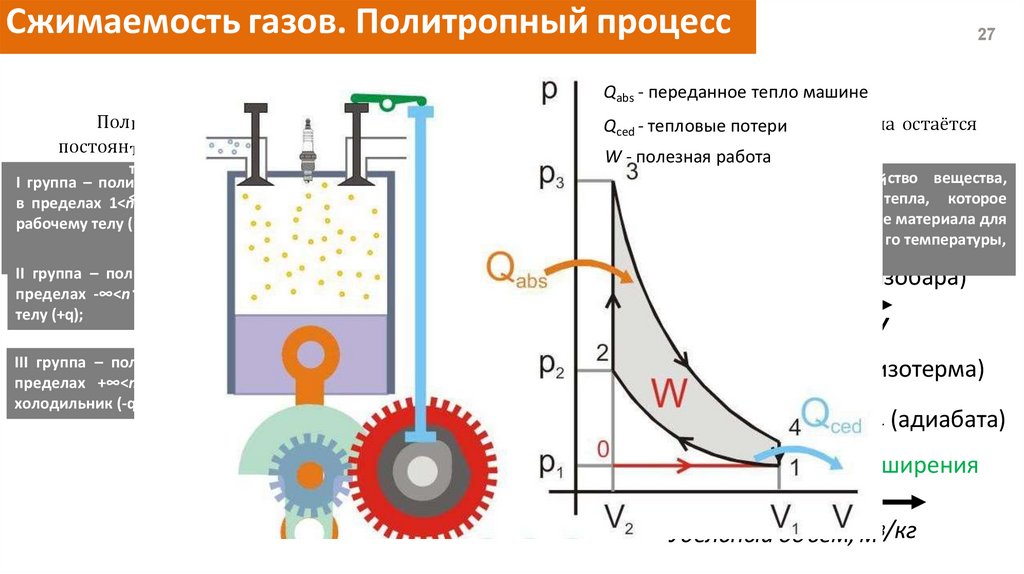
Сжимаемость газов. Политропный процесс
27
PV n const
n=±∞ (изохора)
n=k
Qabs - переданное
тепло машине
P,динПаамическиn=й проц1Q есс,
Политропным называется термо
при котором
- тепловые
потери теплоемкостьла остаётся
ced
постоян те ной.
W - полезная
работа
III
I Теплоемкость - физическое свойство вещества,
тропы, показатель химического
которых изменяется
Молярная
теплоемкость
C Cp
I группа – поли
определяемое как количество тепла, которое
вещества-это
количество
которое
<k, а теплотaэнергии,
q в процессе
подводится к
в пределах 1<n
II
n
должно
быть
добавлено
в
виде
тепла
к
одному
должно
быть
подано
к
данной масс е материала для
рабочему телу ( +q)
C CV
молю вещества, чтобы вызвать увеличение его
получения единичного изменения е го температуры,
[Дж/К].
температуры на одну единицу [Дж/моль∙К].
II группа – пол итропы, показатели которых лежат в
n=0 (изобара)
<1,
с
подводом
теплоты
к
рабочему
пределах -∞<n
Показатель политропы
Процесс
телу (+q);
III группа – политропы, показатели которых лежат в
теплоты от системы в
пределах +∞<n<k с отводомИзобарический
холодильник (-q )
Изотермический
Изохорический
Адиабатический
0
V
n
n=1 (изотерма)
0
II
1 III
I
(адиабата)
n=k
∞
область сжатия k
область рас ширения
n=±∞
Удельный объем, м3/кг

28.

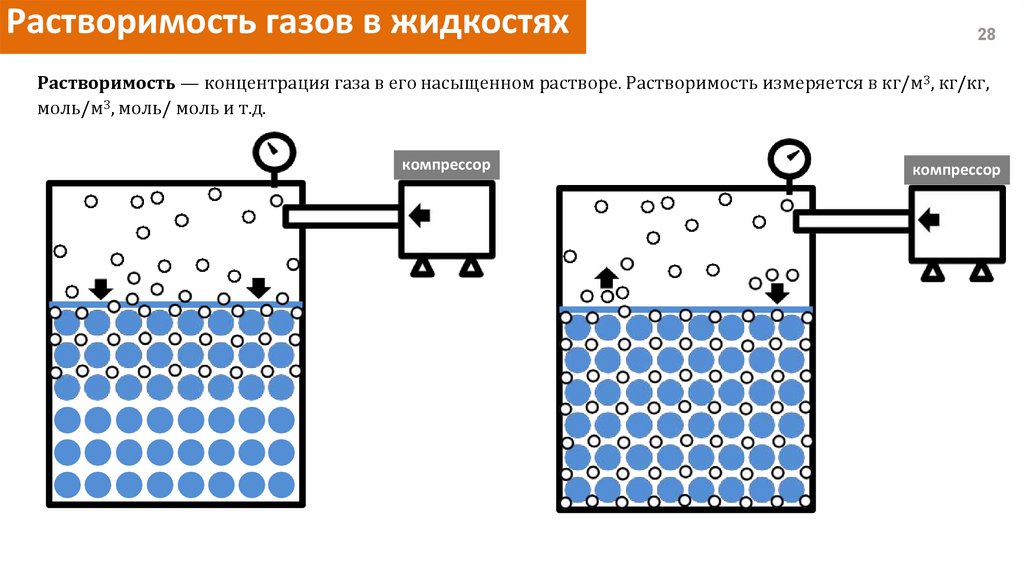
Растворимость газов в жидкостях
28
Растворимость — концентрация газа в его насыщенном растворе. Растворимость измеряется в кг/м3, кг/кг,
моль/м3, моль/ моль и т.д.
компрессор
компрессор

29.

Растворимость газов в жидкостях
29
Принцип Ле-Шателье — если на систему, находящуюся в устойчивом равновесии, воздействовать извне, изменяя
какое-либо из условий равновесия (температура, давление, концентрация), то в системе усиливаются процессы,
направленные на компенсацию внешнего воздействия.
французский физик
и химик Анри Луи
Ле Шателье

30.

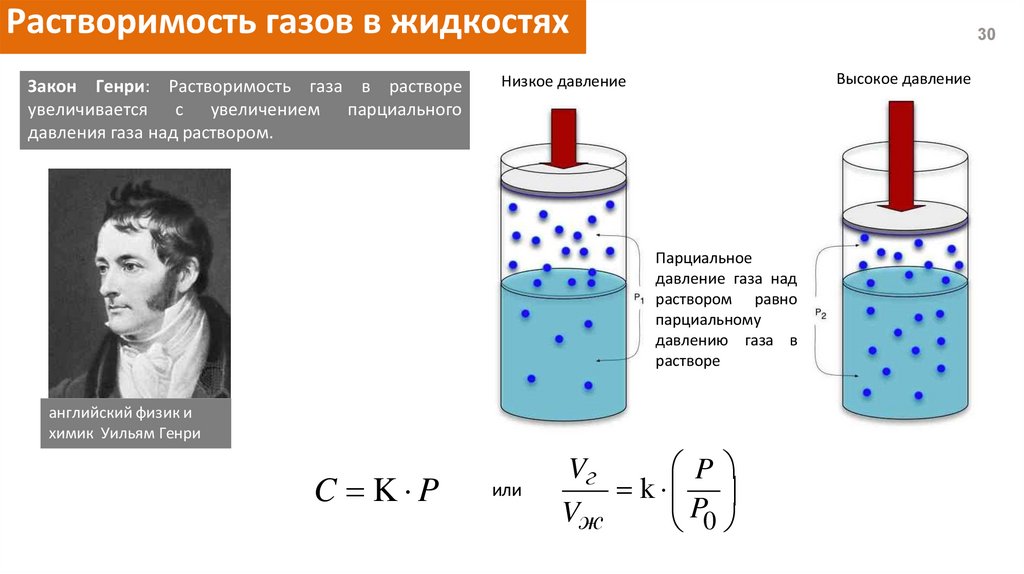
Растворимость газов в жидкостях
Закон Генри: Растворимость газа в растворе
увеличивается с увеличением парциального
давления газа над раствором.
30
Высокое давление
Низкое давление
Парциальное
давление газа над
раствором равно
парциальному
давлению газа в
растворе
английский физик и
химик Уильям Генри
C K P
или
P
Vг
k
Vж
P0

31.

Растворимость газов в жидкостях
31
Растворимость газов k в воде при 1 атм., м3 /м3
СO = 20,9%
Газ
СN = 79,1%
Азот
Водород
Двуокись углерода
Кислород
Температура, °C
2
2
0
20
50
0,024
0,022
1,713
0,049
0,016
0,018
0,878
0,031
0,011
0,016
0,440
0,021
Расчет содержания O2 и N2, растворенных в воде при атмосферном давлении:
O2
Vг
20,9
0,031
1л
100
6,5 мл л
N2
Vг
79,1
0,016
1л
100
13 мл л
Расчет содержания СO2 в воде под давлением давлении 200 кПа:
CO2
Vг
200
0,878
1л
100
1,756 л л

32.

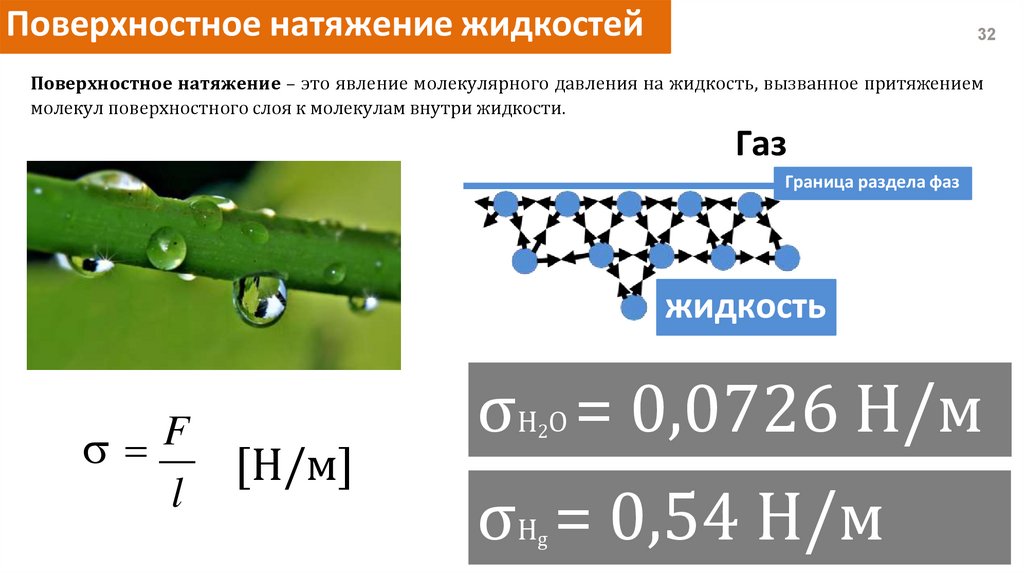
Поверхностное натяжение жидкостей
32
Поверхностное натяжение – это явление молекулярного давления на жидкость, вызванное притяжением
молекул поверхностного слоя к молекулам внутри жидкости.
Газ
Граница раздела фаз
жидкость
F
l
[Н/м]
σH O = 0,0726 Н/м
2
σH = 0,54 Н/м
g

33.

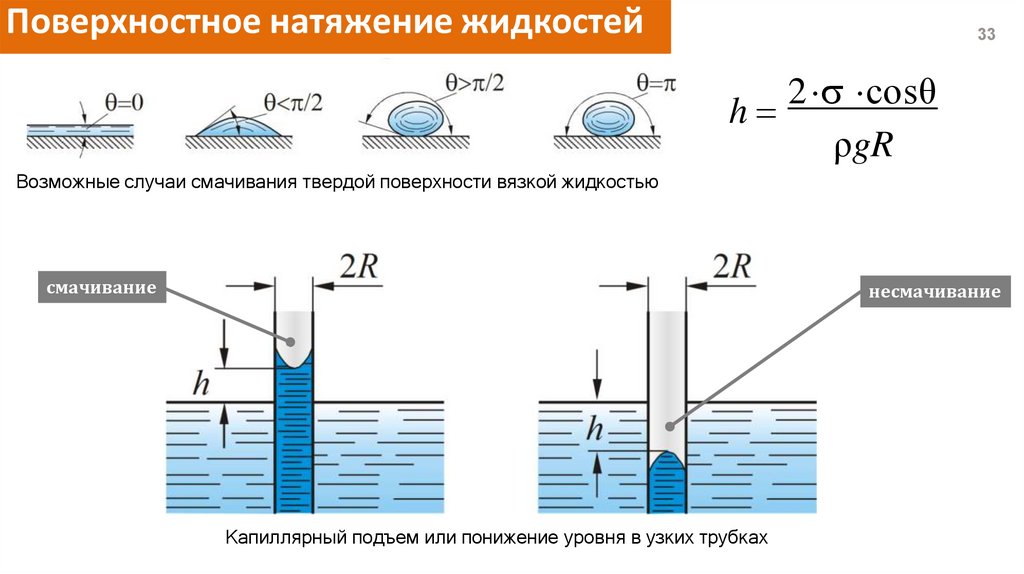
Поверхностное натяжение жидкостей
33
2 cosθ
h
ρgR
Возможные случаи смачивания твердой поверхности вязкой жидкостью
смачивание
несмачивание
Капиллярный подъем или понижение уровня в узких трубках

34.

Кипение жидкости
34
Кипением называется
процесс образования пара внутри объема жидкости, то есть испарение,
перегретая
вода
сопровождающееся интенсивным образованием пузырей внутри объема жидкости, заполненных
насыщенным паром.
0
T, С ↑
P=const
P, ПаT,↓0С ↑
P, Па ↓
T=const

35.

Кавитация
35
Шум от кавитации
Кипение, возника ющее в движущейся среде вследствие местных понижений давления, называется
кавитацией.
Пузырьковая
перемещ ающаяся кавитация
Суперкавитация

36.

Кавитация
36
2 P Pн V02
c
1
V 2
ρV 2

37.

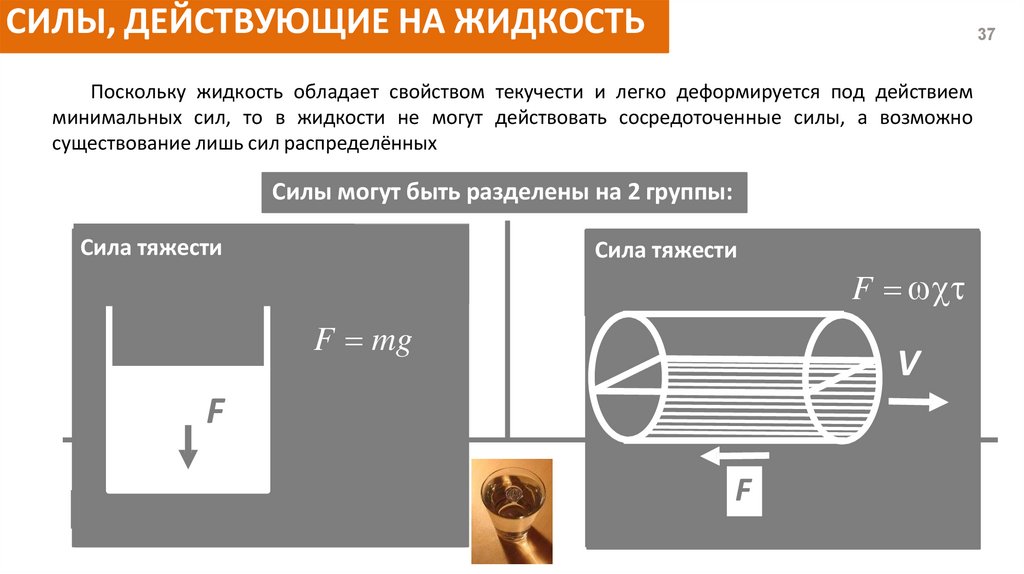
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЖИДКОСТЬ
37
Поскольку жидкость обладает свойством текучести и легко деформируется под действием
минимальных сил, то в жидкости не могут действовать сосредоточенные силы, а возможно
существование лишь сил распределённых
Силы могут быть разделены на 2 группы:
Центробежная
сила силы
Массовые
или объемные
Сила
Сила тяжести
инерции
F в
(действующие на все частицы
рассматриваемом объеме)
- Сила тяжести (вес)
- Сила инерции
- Центробежная сила
F
F
mV 2
R
FF mg
ma
a
+ Сила поверхностного натяжения
Сила давления
Поверхностные
тяжести силы (действующие
на частицы, которые расположены
FF P на
поверхности жидкости)
-
Сила давления
Сила трения
ω
F
F
V

38.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра водопользования и экологии
Авторы:
Кудрявцев Анатолий Валентинович
Федоров Святослав Викторович
Столбихин Юрий Вячеславович
[email protected]