Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца

1. Поняття стійкості автоматичної системи. Математичні ознаки стійкості. Критерій Гурвіца.

Лекція №5.
Поняття стійкості
автоматичної системи.
Математичні ознаки
стійкості. Критерій Гурвіца.

2. План лекції

1. Поняття стійкість
2. Математичні умови стійкості
3. Критерій стійкості Гурвіца.

3. 1. Поняття стійкість

Стійкість об'єкту полягає в його здатність
зберігати свої властивості в умовах, що
змінюються.
Незбуреним рухом САУ називають рух
ідеальної (безінерційної) системи під
впливом заданого зовнішнього сигналу.
Збуреним називають рух реальної САУ
під впливом заданого зовнішнього
сигналу.

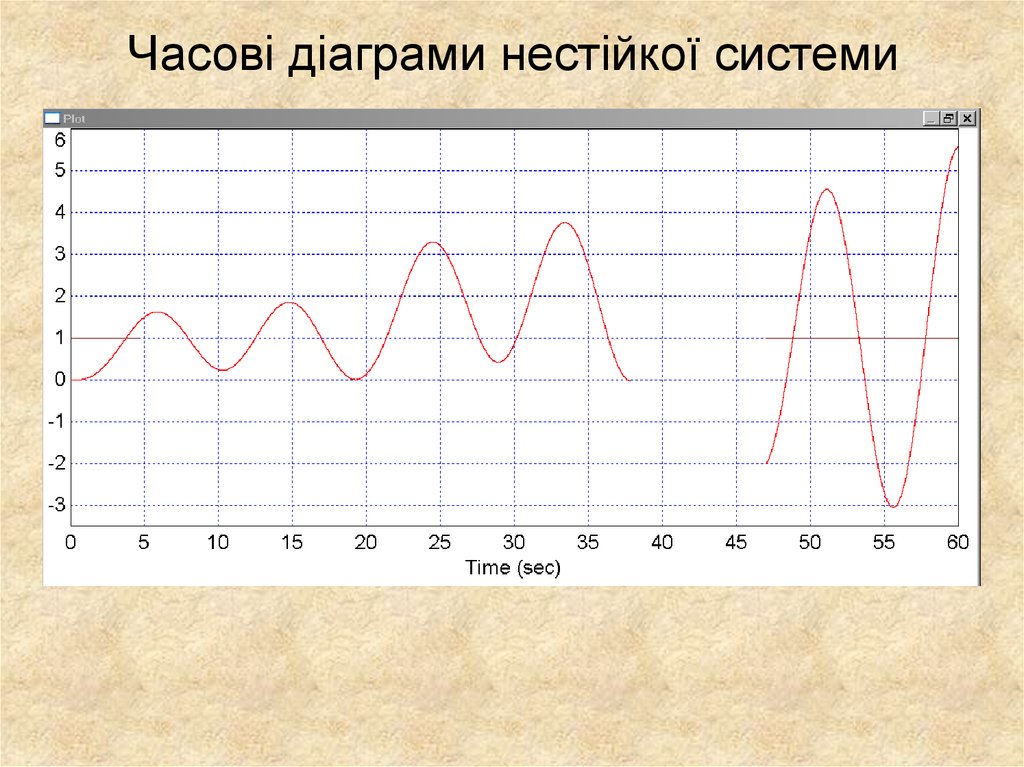
4. Часові діаграми нестійкої системи

5. Часові діаграми системи, що знаходиться на межі стійкості

6. Часові діаграми стійкої системи

Рух є стійким, якщо з часом збурений
рух прагне до незбуреного

7.

Ляпунов, Александр
Михайлович (25 мая (6 июня)
1857, Ярославль — 3 ноября 1918,
Одесса) — русский математик и
механик, академик Петербургской
Академии наук с 1901 года, членкорреспондент Парижской
академии наук. Важнейшим
достижением Ляпунова стало
создание теории устойчивости
равновесия и движения
механических систем.

8. 2. Математичні умови стійкості

an x ( n ) (t ) an 1 x ( n 1) (t ) ..... a1 x (t ) a0 x(t )
bm z ( m ) (t ) bm z ( m ) (t ) ..... b1 z (t ) b0 z(t )
Рішення рівняння, що відповідає збуреному руху:
x(t ) xпер (t ) xнзб (t )
Для того, щоб система була стійкою, необхідно
щоб з часом хпер(t) зменшувалась
lim xпер (t ) 0
t

9.

Рішення однорідного рівняння може бути
отримано у вигляді:
n
xпер (t ) Ci e
i t
i 1
λ i - корені характеристичного рівняння :
n 1
an an 1
n
..... a1 a0 0
Для дійсних коренів характеристичного рівняння
необхідно щоб виконувалась умова:
i 0
Для пари комплексно-споряджених коренів :
k k j k
необхідно щоб:
k 0

10.

Необхідна і достатня ознака
стійкості лінійного об'єкту полягає в
тому, щоб усі корені
характеристичного рівняння мали
негативну дійсну частину.
графічна інтерпритація

11. 3. Алгебраїчний критерій Гурвіца

Критерій стійкості – це умови, виконання
яких необхідно і достатньо, щоб усі
корені характеристичного рівняння
системи, розташовувались в лівій
напівплощині коренів, то б то САУ була
стійкою.

12.

Адольф Гурвиц (нем.
Adolf Hurwitz), 26
березня 1859,
Хильдесхайм — 18
листопада 1919,
Цюрих) — немецкий
математик.

13.

Якщо всі корені алгебраїчного рівняння:
n
a n p a n 1 p
n 1
a n 2 p
n 2
....a 0 0
розташовані зліва, т.т. мають від’ємну
дійсну частину, якщо коефіцієнти
ai 0
i всі визначники Гурвіца починаючи з
головного визначника більше нуля, то система
стійка.

14.

Визначник Гурвіца:
an 1
an 3
an 5
0
an
an 2
an 4
0
n 0
an 1
an 3
0
0
0
0
a0

15.

Визначники Гурвіца для системи 4-го порядку:
4
a3
a1
0
0
a4
a2
a0
0
0
a3
a1
0
0
a4
a2
a0
a3
a1
0
3 a4
a2
a0
0
a3
a1
2
a3
a1
a4
a2
1 a3
Визначники Гурвіца для системи 3-го порядку:
a2
a0
0
3 a3
a1
0
0
a2
a0
2
a2
a0
a3
a1
1 a2

16. Завдання на самопідготовку:

• Абрамов Ю.А. “Основы пожарной
автоматики“ стор. 122-130