Similar presentations:
Наближення функцій
1. НАБЛИЖЕННЯ ФУНКЦІЙ
Задача побудови функції φ (x), яка бприблизно зображувала функцію f(x) з тим чи
іншим ступенем точності, називається задачею
наближення.
• Рівномірне наближення.
• Інтерполяція
• Середньоквадратичне наближення.
2. ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ
.ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ
Задана система вузлів x0 , x1 ,..., xm та значень функції у
вузлах f ( x0 ), f ( x1 ),..., f ( xm ) :
Поліном
( x) a0 0 ( x) a1 1 ( x) a2 2 ( x)... am m ( x)
називається узагальненим поліномом,
де j (x) – система базисних функцій,
a0, a1, ..., am– деякі постійні коефіцієнти.
Системою базисних функцій можуть бути:
k ( x) x k , k 0, m
k ( x) exp( 2 i k x ), k 0, m
k ( x) 1, sin( x ), cos( x), sin( 2 x), cos(2 x ),...
3.
f ( x0 ) a0 0 ( x0 ) a1 1 ( x0 ) a2 2 ( x0 )... am m ( x0 )f ( x1 ) a0 0 ( x1 ) a1 1 ( x1 ) a2 2 ( x1 )... am m ( x1 )
f ( x2 ) a0 0 ( x2 ) a1 1 ( x2 ) a2 2 ( x2 )... am m ( x2 )
...
f ( xm ) a0 0 ( xm ) a1 1 ( xm ) a2 2 ( xm )... am m ( xm )
0 ( x0 ) 1 ( x0 ) 2 ( x0 ) ... m ( x0 )
f ( x0 )
a0
( x ) ( x ) ( x ) ... ( x )
f (x )
a
0
1
1
1
2
1
m
1
1
1
0 ( x2 ) 1 ( x2 ) 2 ( x2 ) ... m ( x2 ) 0; f f ( x2 ) ; a a2 ;
...
...
...
f ( xm )
am
0 ( xm ) 1 ( xm ) 2 ( xm ) ... m ( xm )
a f , a Δ 1 f
4.
f ( x0 ) a0 a1 x01 a2 x02 ... am x0mf ( x1 ) a0 a1 x11 a2 x12 ... am x1m
f ( x2 ) a0 a1 x12 a2 x22 ... am x2m
...
f ( xm ) a0 a1 x1m a2 xm2 ... am xmm
1
1
...
1
1
0
1
1
x
x
...
x1m
...
...
...
...
x
x
0;
...
m
xm
m
0
m
1
f ( x0 )
f (x )
1
f f ( x2 ) ; a
...
f ( xm )
a f , a Δ 1 f
a0
a
1
a 2 ;
...
am
5. НАБЛИЖЕННЯ ФУНКЦІЙ
.НАБЛИЖЕННЯ ФУНКЦІЙ
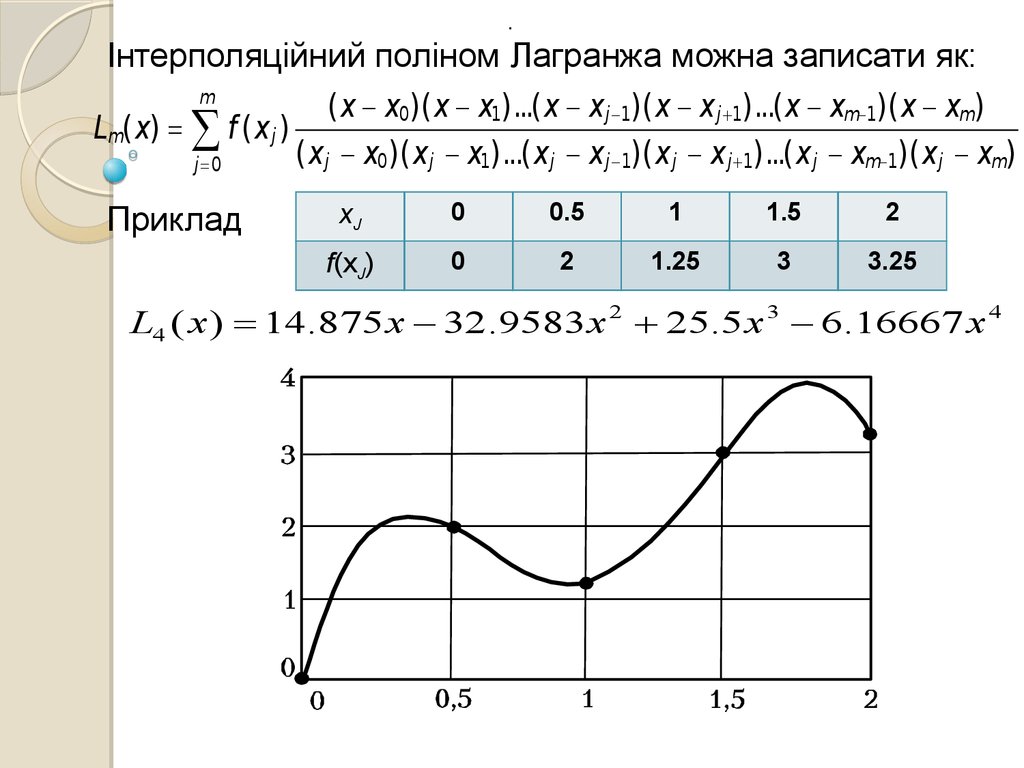
Інтерполяційний поліном Лагранжа можна записати як:
m
Lm ( x) ( x) f ( x j ) j ( x)
j 0
де j (x ) – поліном степеня m, що у вузлах інтерполяції
задовольняє умови:
ì1,для i ,j
j ( x) í
î0,в інших випадках.
Поліном, що задовольняє цим вимогам:
( x x0)( x x1)...( x x j 1)( x x j 1)...( x xm 1)( x xm)
j ( x)
( x j x0)( x j x1)...( x j x j 1)( x j x j 1)...( x j xm 1)( x j xm)
6.
7.
.Інтерполяційний поліном Лагранжа можна записати як:
m
( x x0)( x x1)...( x xj 1)( x x j 1)...( x xm 1)( x xm)
Lm( x) f ( xj )
( xj x0)( xj x1)...( x j xj 1)( xj x j 1)...( xj xm 1)( xj xm)
j 0
Приклад
xJ
0
0.5
1
1.5
2
f(xJ)
0
2
1.25
3
3.25
L4 ( x ) 14.875 x 32.9583 x 2 25.5 x 3 6.16667 x 4
8. ПОХИБКИ ФОРМУЛИ ЛАГРАНЖА
.ПОХИБКИ ФОРМУЛИ ЛАГРАНЖА
Різницю між функцією та її інтерполяційним наближенням
називають залишковим членом інтерполяційної формули або
похибкою інтерполяції:
rm ( x) Lm ( x) f ( x)
Для полінома Лагранжа маємо:
f ( m 1) (z )
rm ( x)
w ( x),
(m 1)!
M m 1 max | f ( m 1) ( x) |
[ a ,b ]
M m 1
w ( x),
(m 1)!
де w ( x) ( x x0 )( x x1 )...( x xm ).
| f ( x) Lm ( x) | £
Коли функція f (x) є поліномом степеня m, інтерполяційний
поліном на вузлах x0 , x1 ,..., xm є точним, тобто:
Lm ( x) f ( x)
9.
y = ln xx
1.0
1.1
1.2
1.3
1.4
y
0.000
0.95310
0.182322
0.262364
0.336472
x = 1.23;
x0 = 1.1; x1= 1.2;
x0 = 1.1; x1= 1.2; x2= 1.3;
L1(1.23) = 0.206335;
L2(1.23) = 0.207086;
10.
M2| f ( x) L1 ( x) | £
| ( x x0 )( x x1 ) |,
2
M
| f ( x) L2 ( x) | £ 3 | ( x x0 )( x x1 )( x x2 ) | .
6
1
1
( 2)
f ( x) ln( x) f ( x) 2 M 2 max | f ( x) | 2 0.69
[1.2 ,1.3]
x
1.2
2
2
( 3)
( 3)
f ( x) 3 M 3 max | f ( x) | 3 1.5
[1.2 ,1.3]
x
1.1
( 2)
0.69
1 | ln(1.23) L1 ( x) | £
| (1.23 1.2)(1.23 1.3) | 7.3 *10 4 ,
2
1.5
2 | ln(1.23) L2 ( x) | £ | (1.23 1.1)(1.23 1.2)(1.23 1.3) | 6.9 *10 5 ,
6
11.
.Скінченні різниці першого порядку:
f ( x0 ) f ( x1 ) f ( x0 ),
f ( x1 ) f ( x2 ) f ( x1 ),
...
f ( xm 1 ) f ( xm ) f ( xm 1 ).
Скінченні різниці другого порядку:
2 f ( x0 ) f ( x1 ) f ( x0 ),
2 f ( x1 ) f ( x2 ) f ( x1 ),
...
2 f ( xm 2 ) f ( xm 1 ) f ( xm 2 ).
У загальному випадку скінченні різниці k-го порядку:
k f ( xi ) k 1 f ( xi 1 ) k 1 f ( xi ).
12.
.ВЛАСТИВОСТІ СКІНЧЕННИХ РІЗНИЦЬ
1. Скінченні різниці сталої дорівнюють нулю.
2. Сталий множник можна виносити за знак
скінченної різниці.
3. Якщо f (x) − многочлен степеня m, то різниця
f ( x) 0для k > m.
k
f (x)
4. Якщо m-і різниці функції
сталі, то ця
функція є многочленом степеня m.
13.
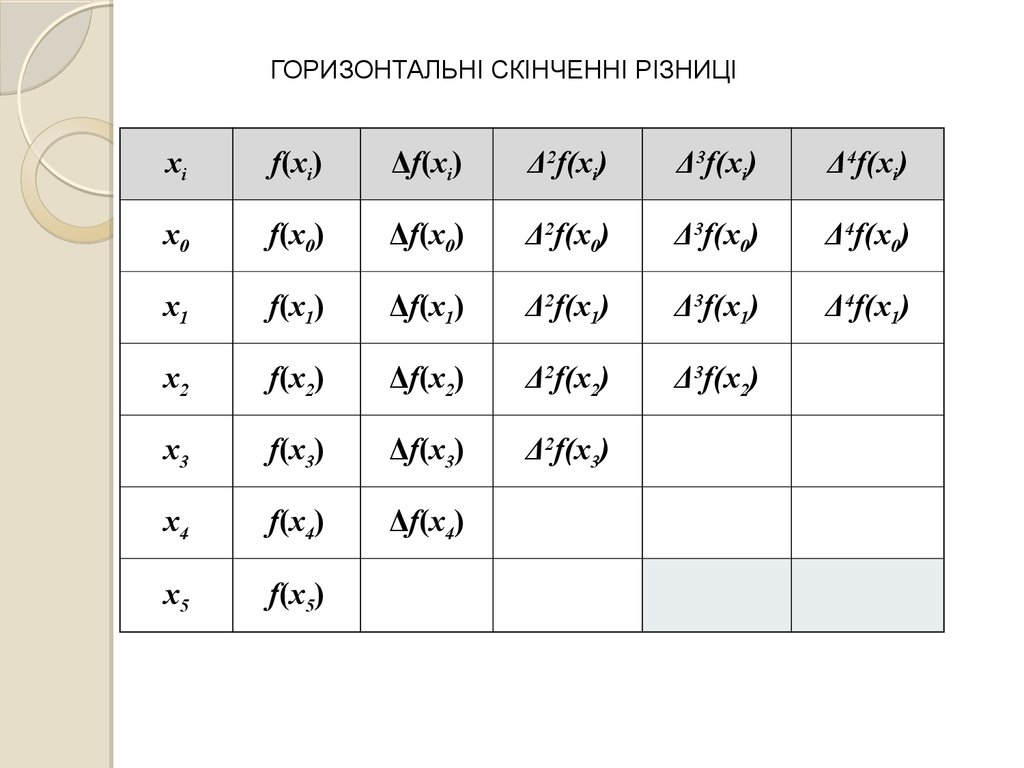
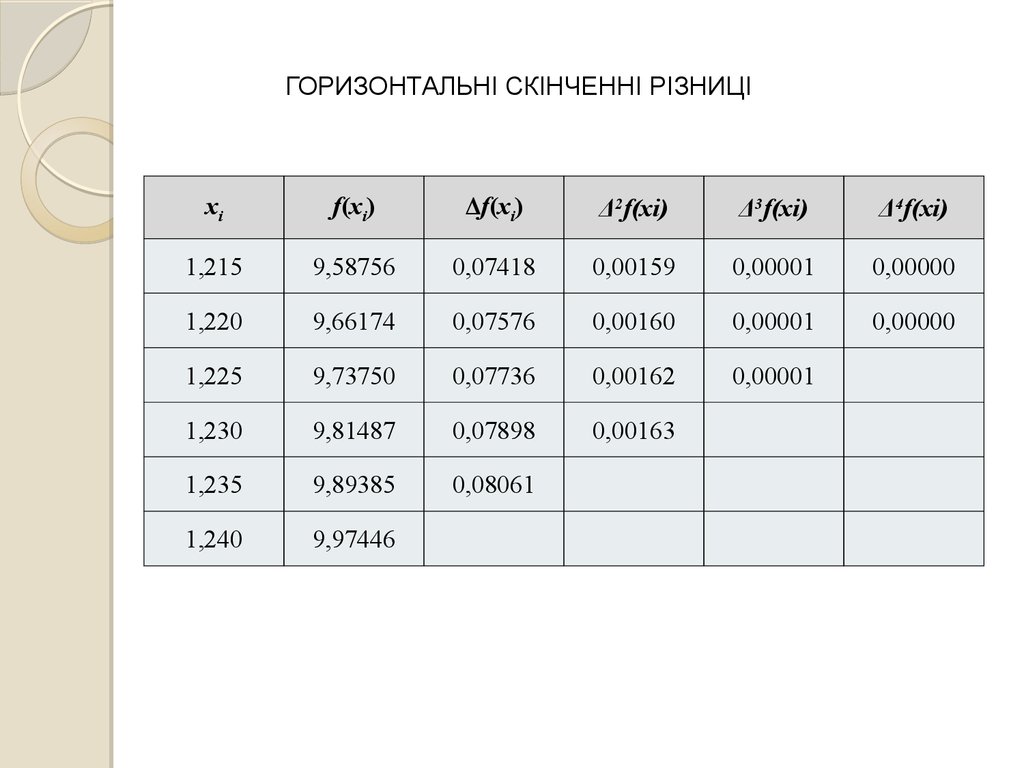
ГОРИЗОНТАЛЬНІ СКІНЧЕННІ РІЗНИЦІxi
f(xi)
Δf(xi)
Δ2f(xi)
Δ3f(xi)
Δ4f(xi)
x0
f(x0)
Δf(x0)
Δ2f(x0)
Δ3f(x0)
Δ4f(x0)
x1
f(x1)
Δf(x1)
Δ2f(x1)
Δ3f(x1)
Δ4f(x1)
x2
f(x2)
Δf(x2)
Δ2f(x2)
Δ3f(x2)
x3
f(x3)
Δf(x3)
Δ2f(x3)
x4
f(x4)
Δf(x4)
x5
f(x5)
14.
ГОРИЗОНТАЛЬНІ СКІНЧЕННІ РІЗНИЦІxi
f(xi)
Δf(xi)
Δ2f(xi)
Δ3f(xi)
Δ4f(xi)
1,215
9,58756
0,07418
0,00159
0,00001
0,00000
1,220
9,66174
0,07576
0,00160
0,00001
0,00000
1,225
9,73750
0,07736
0,00162
0,00001
1,230
9,81487
0,07898
0,00163
1,235
9,89385
0,08061
1,240
9,97446
15.
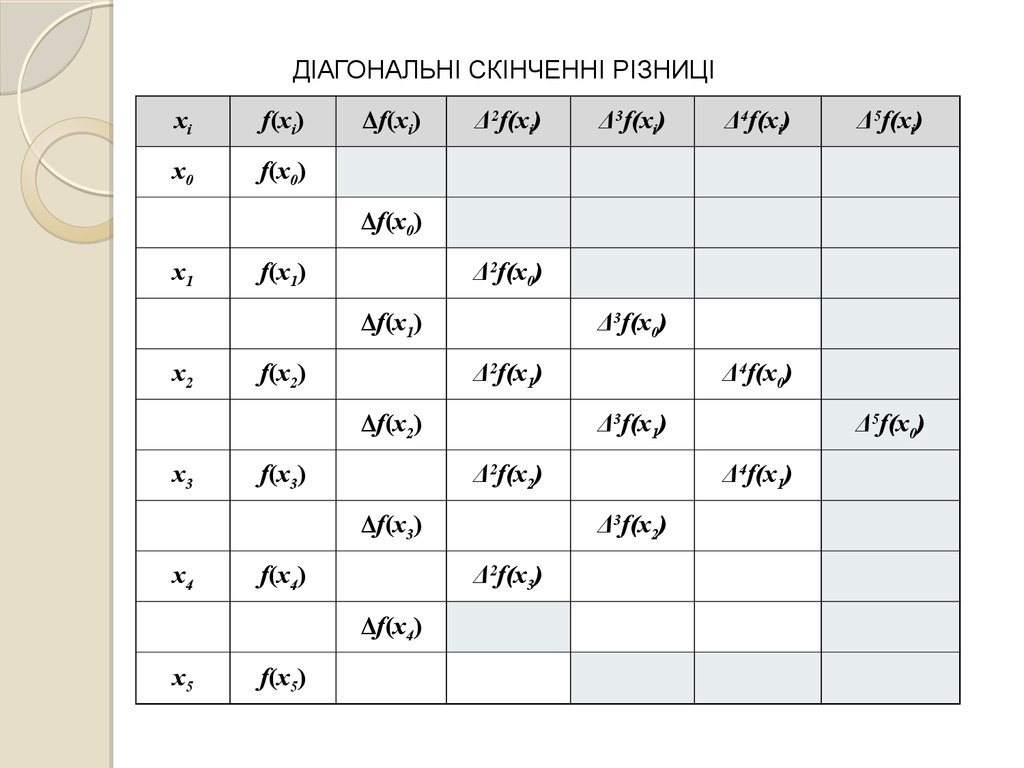
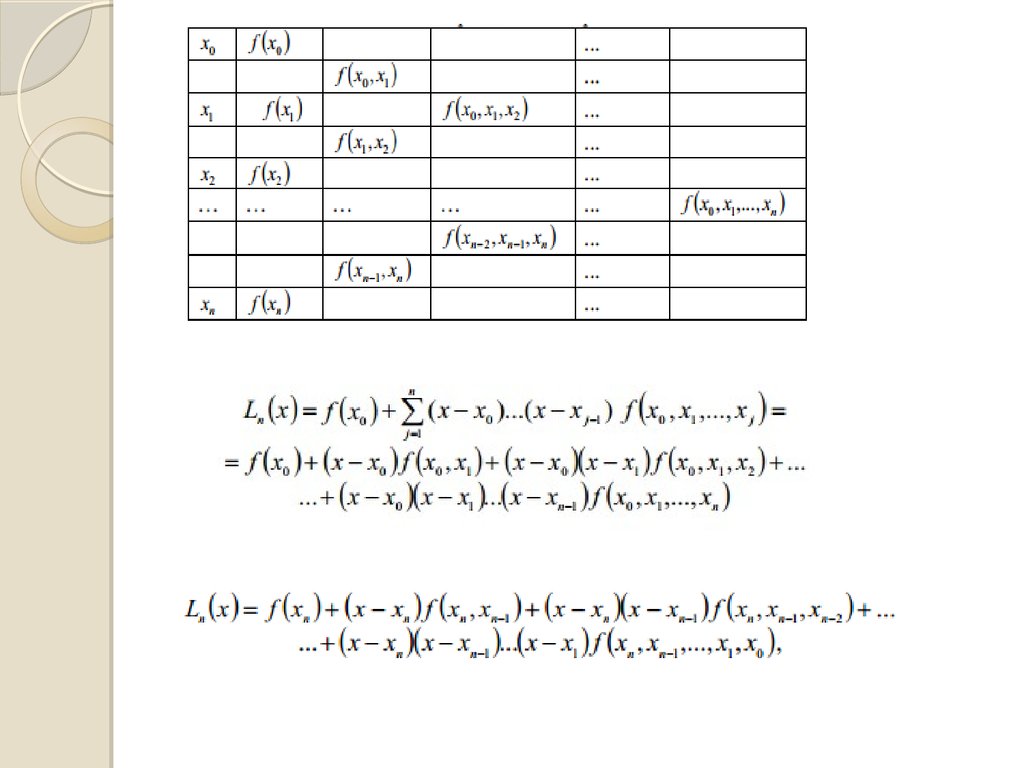
ДІАГОНАЛЬНІ СКІНЧЕННІ РІЗНИЦІxi
f(xi)
Δf(xi)
Δ2f(xi)
Δ3f(xi)
Δ4f(xi)
Δ5f(xi)
x0
f(x0)
Δf(x0)
f(x1)
Δ2f(x0)
Δf(x1)
f(x2)
Δf(x2)
f(x3)
Δf(x3)
f(x4)
Δ2f(x3)
Δf(x4)
f(x5)
x1
x2
x3
x4
x5
Δ3f(x0)
Δ2f(x1)
Δ4f(x0)
Δ3f(x1)
Δ2f(x2)
Δ5f(x0)
Δ4f(x1)
Δ3f(x2)
16.
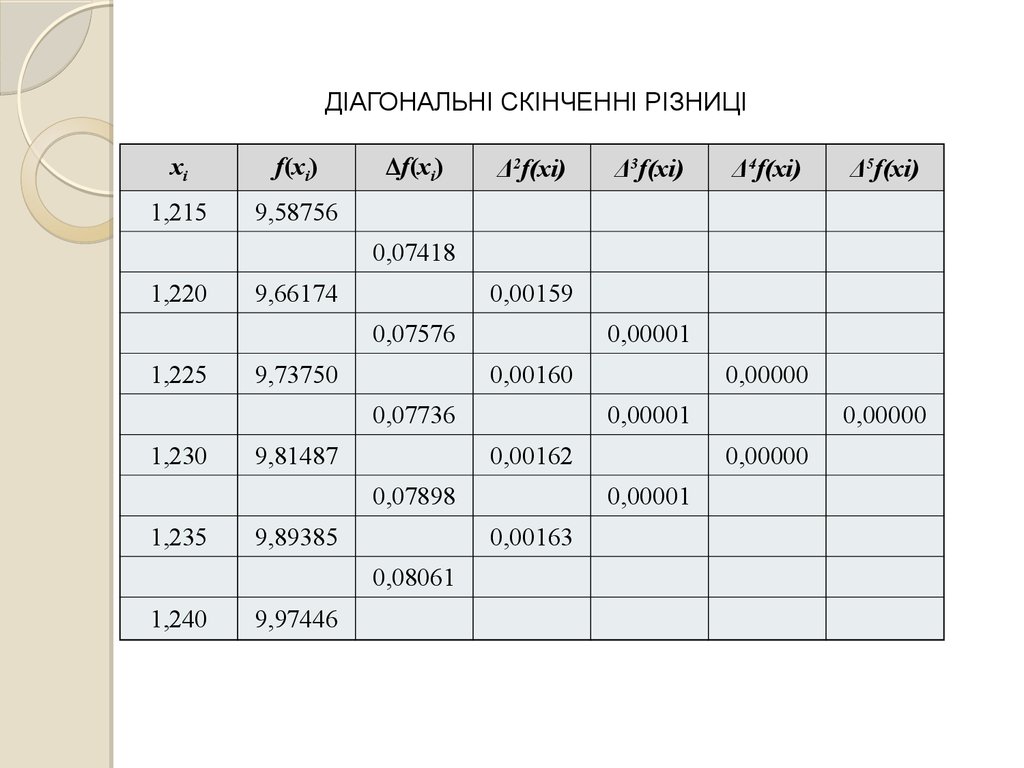
ДІАГОНАЛЬНІ СКІНЧЕННІ РІЗНИЦІxi
f(xi)
9,58756
1,215
0,07418
0,00159
0,00001
0,00160
9,89385
0,00000
0,00162
0,00000
0,00001
0,00163
0,08061
9,97446
0,00000
0,00001
0,07898
1,240
9,81487
1,235
Δ5f(xi)
0,07736
Δ4f(xi)
0,07576
1,230
Δ3f(xi)
9,73750
1,225
Δ2f(xi)
9,66174
1,220
Δf(xi)
17. ПЕРША ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА
.ПЕРША ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА
Нехай, вузли інтерполяції x0 , x1 ,..., xm розташовані
рівномірно: x0 , x1 x0 h, x2 x0 2h,..., xm x0 mh.
Побудуємо інтерполяційний поліном у вигляді:
N m ( x) a0 a1 ( x x0 ) a2 ( x x0 )( x x1 ) ... am ( x x0 )...( x xm 1 )
Задача полягає в обчисленні значень
Покладемо
a0 , a1 ,..., am .
x x0 ,то f ( x0) N m( x0) a0.
Покладемо x x1.
f ( x1 ) N m ( x1 ) a0 a1 ( x1 x0 ) f ( x0 ) a1h.
f ( x0 )
Звідки a1
.
h
18.
Для x x2 маємо:f ( x2 ) N m ( x2 ) a0 a1 ( x2 x0 ) a2 ( x2 x0 )( x2 x1 ).
Враховуючи, що ( x2 x0 ) 2h та ( x2 x1 ) h :
2
f ( x0 )
2
f ( x2 ) 2 f ( x1 ) f ( x0 ) a2 2! h , a2
.
2
2! h
Аналогічно, для x x3
f ( x3 ) 3 f ( x2 ) 3 f ( x1 ) f ( x0 ) 3 f ( x0 )
a3
.
3
3
3! h
3! h
Для x xk маємо:
k f ( x0 )
ak
(k 1, 2...m).
k
k !h
19.
Таким чином, маємо :f ( x0 )
2 f ( x0 )
N m ( x) a0
( x x0 )
( x x0 )( x x1 )
2
h
2!h
3 f ( x0 )
k f ( x0 )
( x x0 )( x x1 )( x x2 ) ...
( x x0 )...( x xk 1 ) ...
3
k
3!h
k !h
m f ( x0 )
( x x0 )( x x1 )...( x xm 1 ).
m
m !h
Завдання
x x0
Покласти t
і отримати іншу
h
форму запису першої інтерполяційної формули Ньютона.
20. ДРУГА ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА
.ДРУГА ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА
Нехай, вузли інтерполяції x0 , x1 ,..., xm розташовані
рівномірно: x0 , x1 x0 h, x2 x0 2h,..., xm x0 mh.
Побудуємо інтерполяційний поліном у вигляді:
N m ( x) a0 a1 ( x xm ) a2 ( x xm )( x xm 1 ) ... am ( x xm )...( x x1 )
Задача полягає в обчисленні значень
a0 , a1 ,..., am .
Покладемо x xm ,то f ( xm) N m( xm) a0.
Покладемо x xm 1.
f ( xm 1 ) N m ( xm 1 ) a0 a1 ( xm 1 xm ).
f ( xm ) f ( xm 1 ) f ( xm 1 )
Звідки a1
.
( xm xm 1 )
h
21.
Для x xm 2 маємо:f ( xm 2 ) N m ( xm 2 ) a0 a1 ( xm 2 xm ) a2 ( xm 2 xm )( xm 2 xm 1 ).
f ( xm ) 2 f ( xm 1 ) f ( xm 2 ) 2 f ( xm 2 )
a2
.
2
2
2!h
2!h
Аналогічно, для x xk маємо:
k f ( xm k )
ak
(k 1, 2...m).
k
k !h
22.
Таким чином, маємо :f ( xm 1 )
f ( xm 2 )
N m ( x) f ( xm )
( x xm )
( x xm )( x xm 1 )
2
h
2!h
3 f ( xm 3 )
( x xm )( x xm 1 )( x xm 2 ) ...
3
3!h
m f ( x0 )
( x xm )( x xm 1 )...( x x1 ).
m
m !h
Завдання
x xm
Покласти t
і отримати іншу
h
форму запису другої інтерполяційної формули Ньютона.
2
23.
t( t 1) 2N m( t) f ( x0) t f ( x0)
f ( x0) ...
2!
t( t 1)...( t ( m 1)) m
...
f ( x0).
m!
t( t 1) 2
N m(t) f ( xn ) t f ( xm 1)
f ( xm 2) ...
2!
t( t 1)...(t m 1) m
...
f ( x0).
m!
24. ВИБІР ВУЗЛІВ ІНТЕРПОЛЯЦІЇ
Похибки інтерполяційних формул дорівнюють добутку( m 1)
(x), залежить від
двох множників, з яких один, f
властивостей функції і не піддається корегуванню, а
величина w m 1( x) ( x x0)( x x1)( x x2)...( x xm 1)( x xm)
визначається винятково вибором вузлів інтерполяції.
( m 1)
f
( x)
rm( x)
w m 1( x).
( m 1) !
Задача про раціональний вибір вузлів інтерполяції
(для заданого m) полягає у знаходженні найменшого
максимального значення w m 1( x).
Вузли задаються:
2i 1
x i cos
,
2m 2
( i 1, 2, ..., m).
25.
26.
27.
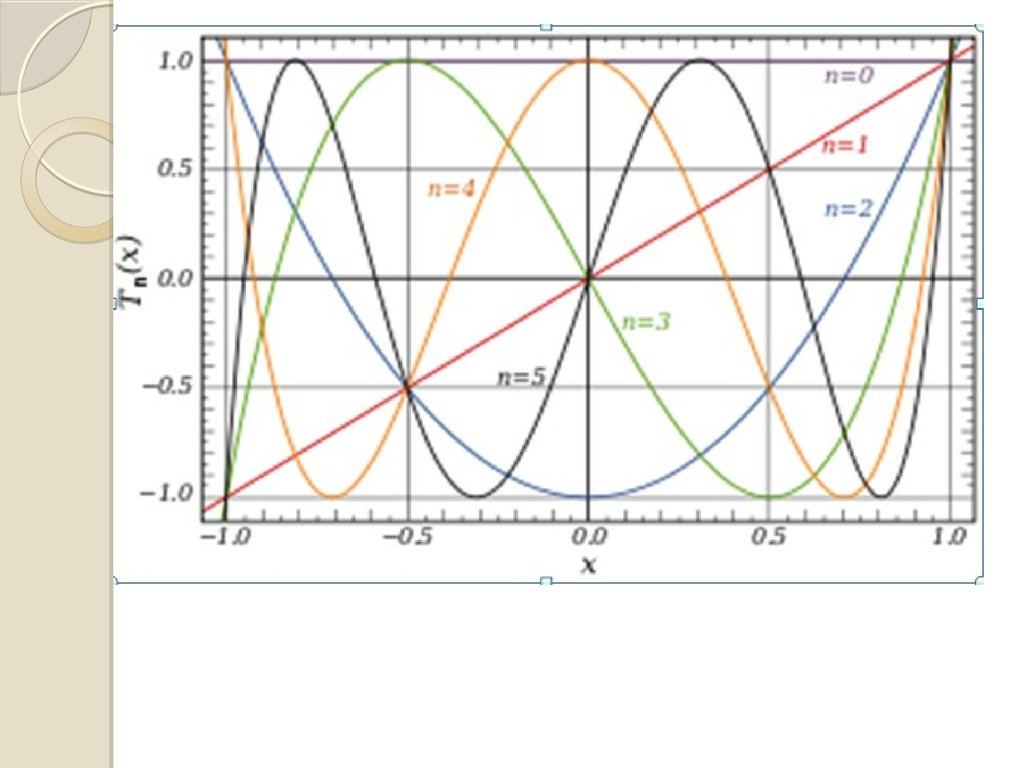
Поліноми Чебишева першого родуможуть бути
визначені за допомогою рекурсивних співвідношень (n>=2)
:
28.
29. ЗБІЖНІСТЬ ІНТЕРПОЛЯЦІЙНОГО ПРОЦЕСУ
Збільшення кількості вузлів інтерполяції з метоюзменшення похибки f ( x) Lm( x) не завжди
виправдане. Необхідно досліджувати збіжність
інтерполяційного процесу. Для цього вводять систему
сіток, а саме:
S0 {x00},
1
1
1
S {x0, x1 },
...
...
...
m
Sm {x0m, x1m, ..., xm
},
m
Теорема Фабера: За будь-якої послідовності сіток S
знайдеться неперервна на відрізку [a, b] функція f ( x),
що послідовність інтерполяційних поліномів
P0( x), P1( x),..., Pm( x), побудованих на послідовності
f ( xдо
)
сіток, не збігатиметься
.
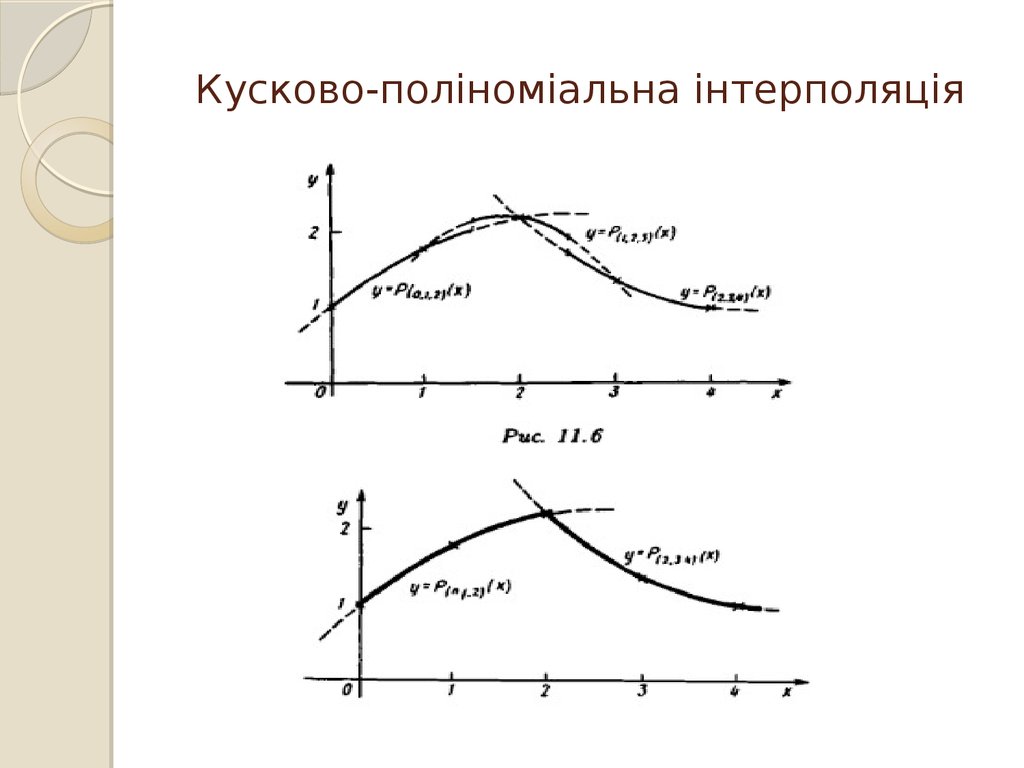
30. Кусково-поліноміальна інтерполяція
31. СПЛАЙНИ
Поліном третього степеня називається кубічнимсплайном
що відповідає функції
і заданий
на сітці вузлів a x1 < x2 < ... < xm=
b, якщо
задовольняються такі умови:
• на кожному відрізку [xi , xi 1], i 1, m
1
функція
є поліномом третього степеня:
2
3
S( x) Si ( x) ai bi ( x xi ) ci ( x xi ) di ( x xi ) ,
xi „ x „ xi 1.
• функція
а також її перша і друга похідні
наперервні на відрізку
• у вузлах інтерполяції S( xi ) f ( xi ), i 1, m.
Доведення існування кубічного сплайна і того, що такий
сплайн тільки один, містить спосіб його побудови.
Кількість невідомих коефіцієнтів – (4m -4).
32.
СЛАР для обчислення коефіцієнтів сплайна:Si ( xi ) f ( xi ), i 1, m;
Si ( xi ) Si 1( xi ), i 2, m 1;
S 'i ( xi ) S 'i 1( xi ), i 2, m 1;
S ''i ( xi ) S ''i 1( xi ), i 2, m 1;
S ''1( x1) 0,
S ''m( xm) 0.
СЛАР з (4m – 4) рівнянь має (4m – 4) невідомих
коефіцієнтів.
33.
Дану СЛАР після перетворень можна звести до СЛАР зтридіагональною матрицею виду:
f ( xi 1 ) f ( xi ) h
(ci 2 2ci 1 )
h
3
f ( xi ) f ( xi 1 ) h
(ci 1 2ci ) 2ci h ci 1 ci , i 1, m 1;
h
3
де c1 0, cm 3d m h,
ci 1 ci
ai f ( xi ), di
,
3h
f ( xi 1 ) f ( xi ) h
bi
(ci 2 2ci 1 ),
h
3
34.
Теорема. Нехай функція f(x)C4[a,b]. Тоді для кубічного
сплайну S(x), побудованого на системі вузлів
a x1 < x2 < ... < xm=
b, справедливі нерівності:
max | f(x) S ( x) | £ M 4 h 4 ,
[ a ,b ]
max | f ¢(x) S ¢( x) | £ M 4 h3 ,
[ a ,b ]
max | f ¢¢(x) S ¢¢( x) | £ M 4 h ,
2
[ a ,b ]
де
M 4 max | f (4) (x)|, h max (xm 1 xm | .
[ a ,b ]
Звідси випливає, що при h
m
0 послідовність функцій S(k)
(x), k=0,1,2 (кубічний сплайн та його перші дві похідні)
збігається до
f(k)(x), відповідно.
35.
36.
{x{a[1]={(0, a[2]
0), =
(0.5,
2), (1.,
2.25),
i,f(xi)} = 2,
2.25,
a[3]
= 3, (1.5, 3), (2,3.25),
(2.5,
(3, 6),a[5]
(3.5,
0.75),
a[4]3),
= 3.25,
=3,
a[6](4,
=6,3.75)};
a[7] = 0.75, a[8] = 3.75,
{b[1]= 2.45238, b[2] = 5.54762, b[3] = –3,
b[4] = 4.04762, b[5] = –2.45238,b[6]
=4.90476,
b[7] = 16.1429, b[8] = 33.7619,
с[1] = 2.28719 10–17, с[2] = 6.19048,
с[3]= –7.80952, с[4] = 2.38095, с[5]= –
9.42857,
с[6]= –19.0476, с[7]=13.5238, с[8]= –
79.5238,
d[1]= 3.09524, d[2]= –13.1905,
d[3]=12.9048,
d[4]= –8.28571, d[5]= 4.61905, d[6]=
37.
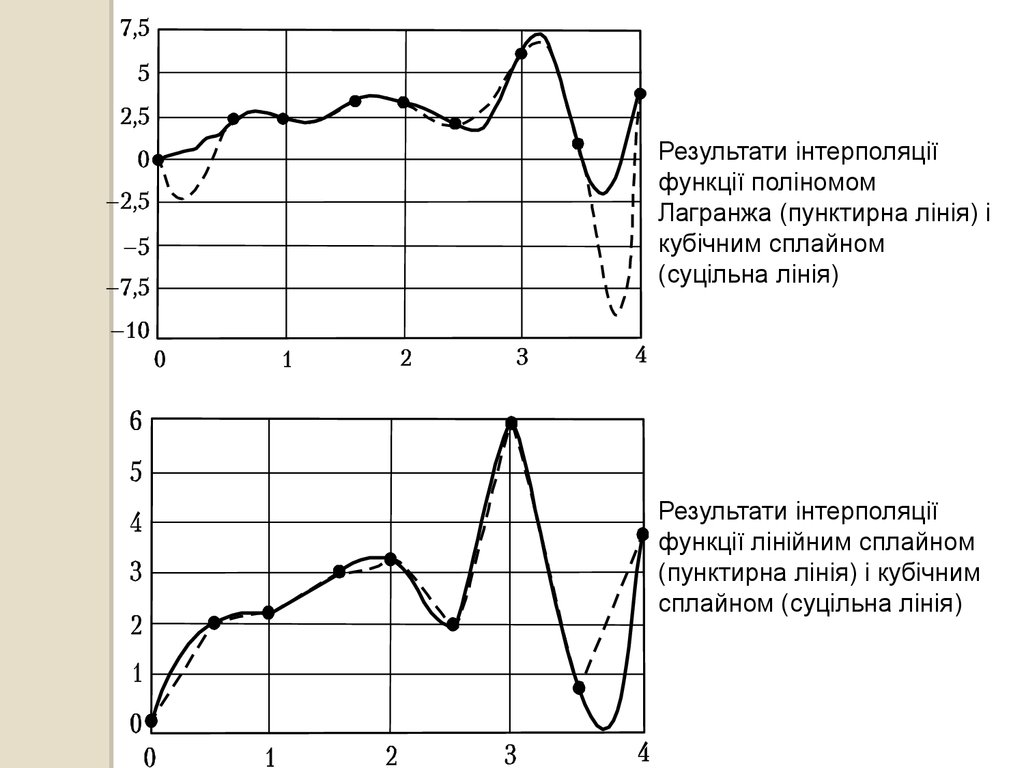
Результати інтерполяціїфункції поліномом
Лагранжа (пунктирна лінія) і
кубічним сплайном
(суцільна лінія)
Результати інтерполяції
функції лінійним сплайном
(пунктирна лінія) і кубічним
сплайном (суцільна лінія)
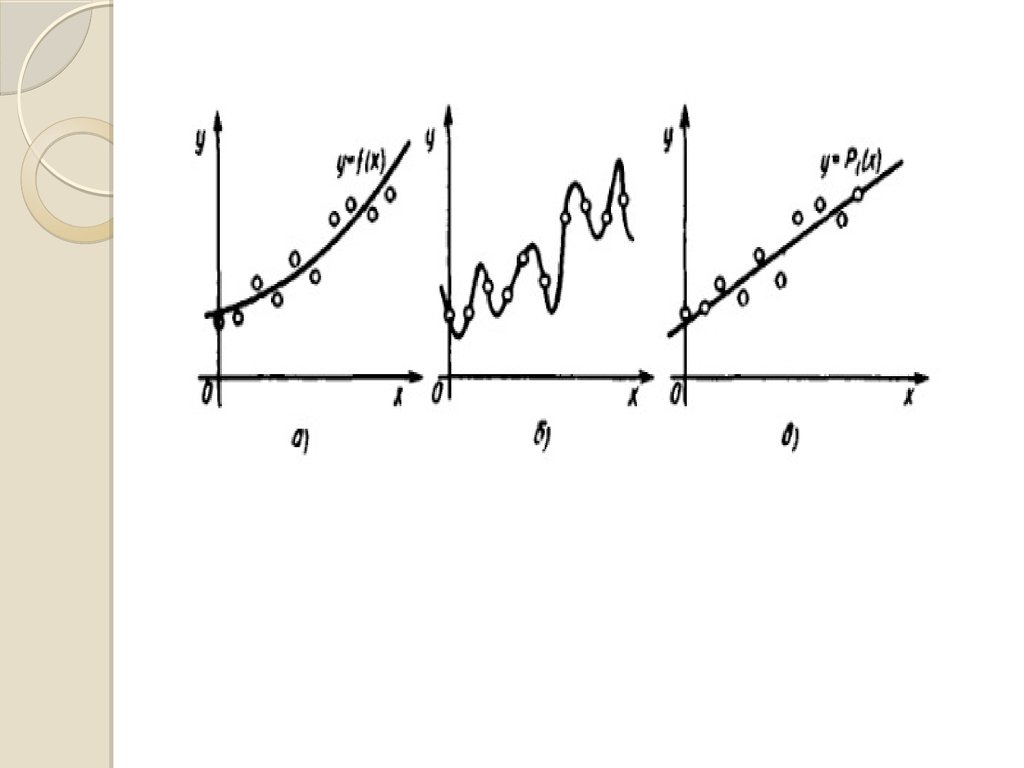
38. МЕТОД НАЙМЕНШИХ КВАДРАТІВ
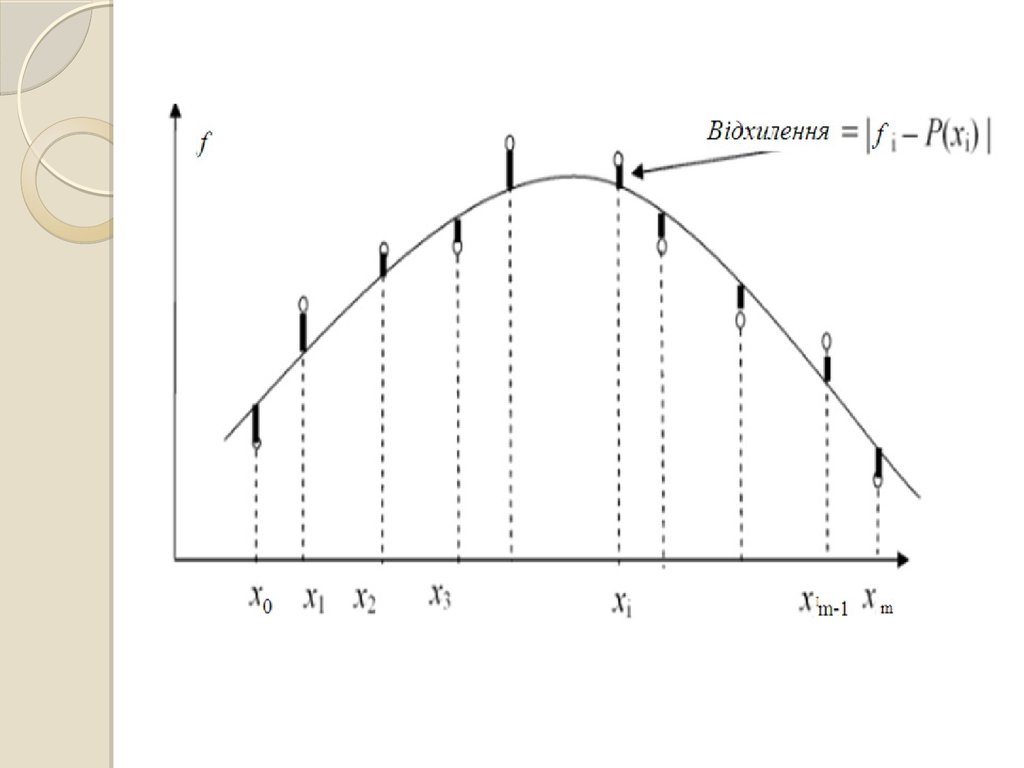
Міра відхилення заданих значень від обраної функціїу заданих m 1 точках ( xi , f ( xi )), i 0,1, 2, ..., m:
I
m
2
(
f
(
x
)
P
(
x
))
i k i min.
i 0
повинна бути мінімальною.
Задамо
2
k
Pk ( x) a0 a1x a2 x ... ak x ,
I
m
k < m,
2
k
2
[
a
a
x
a
x
...
a
x
f
(
x
)]
min.
k i
i
0 1i 2 i
i 0
39.
40.
Необхідно, щоб для всіх коефіцієнтіввиконувалась умова:
¶I
0, i 0, m.
¶ai
Почнемо з a0
m
¶I
2
k
2 [a0 a1xi a2 xi ... ak xi f ( xi )]1 0.
¶a0
i 0
Далі продовжимо для всіх ai
m
¶I
2 [a0 a1xi a2 xi 2 ... ak xi k f ( xi )] x j i 0,
¶a j
i 0
j 1, k.
41.
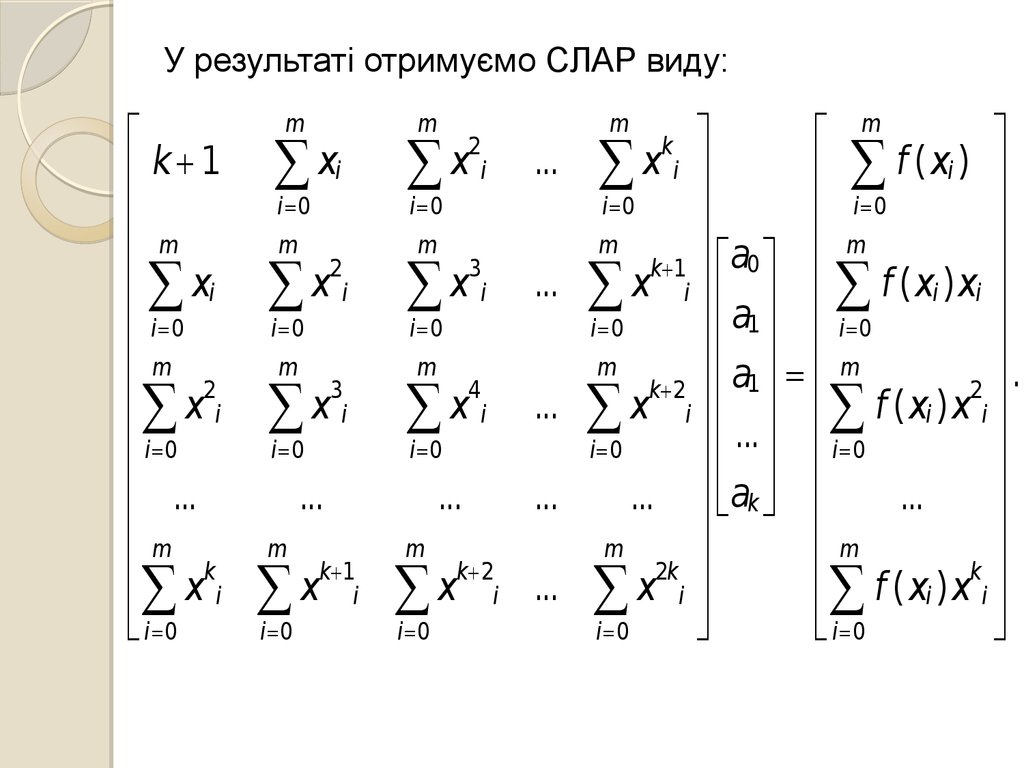
У результаті отримуємо СЛАР виду:k 1
m
xi
i 0
m
x2i
i 0
...
m k
x i
i 0
m
xi
i 0
m
x
2
i
m
2
x
i
...
i 0
m
x
3
i
...
3
x
i
4
x
i
...
...
...
...
x
...
i 0
m
i 0
m
x
i 0
k 1
i
i 0
m
i 0
m
i 0
k 2
i
m
k
x i
f ( xi )
i 0
i 0
m
m
a
0
k 1
x i a1 f ( xi ) xi
i 0
i 0
m
a1 m
.
k 2
2
x
f
(
x
)
x
i ... i i
i 0
i 0
... ak
...
m
m
2k
k
f ( xi ) x i
x i
i 0
i 0
m
42.
43.
44.
45.
46.
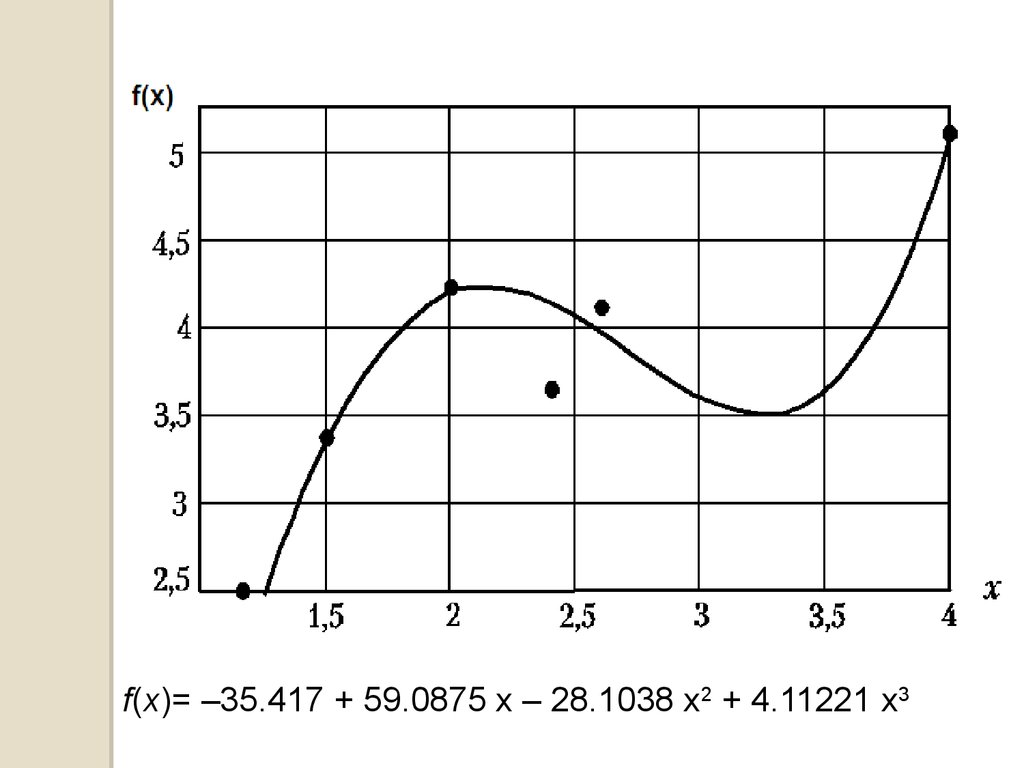
f(x)= –35.417 + 59.0875 x – 28.1038 x2 + 4.11221 x347.
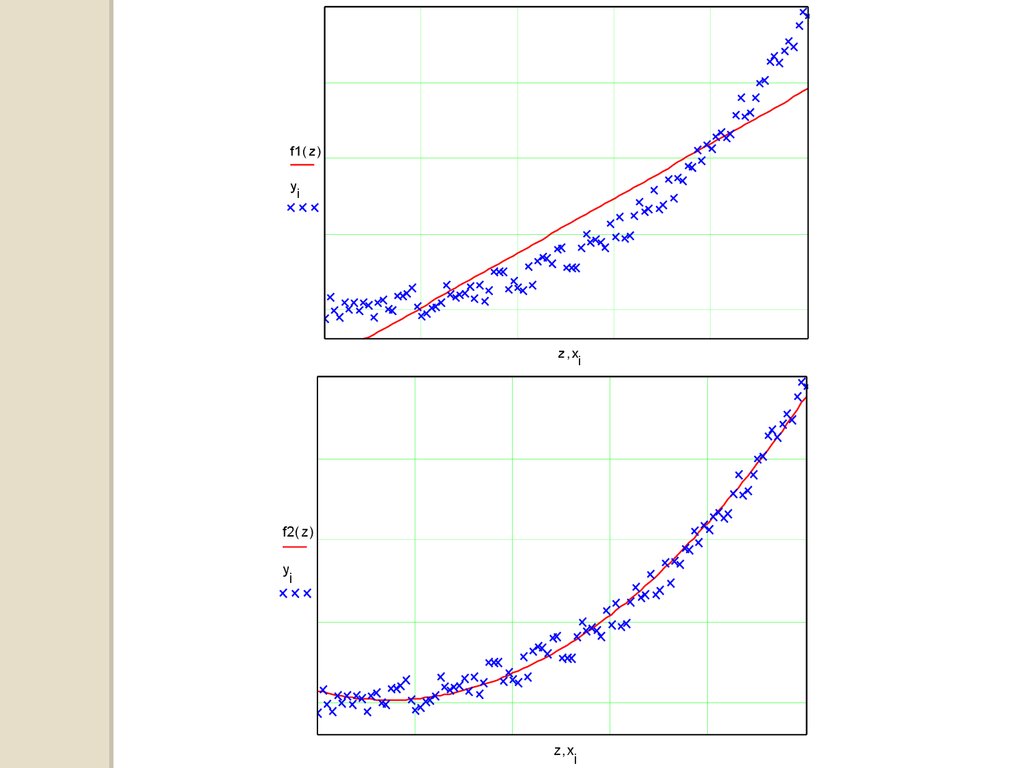
f1( z )y
i
z,x
i
f2( z )
y
i
z,x
i


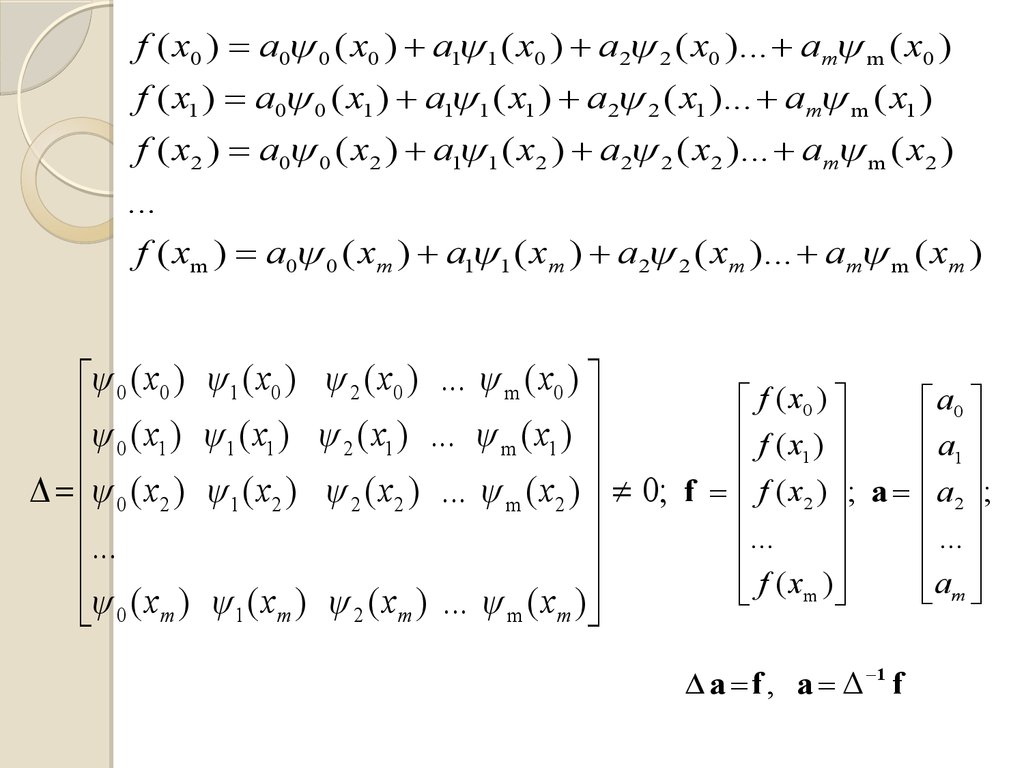





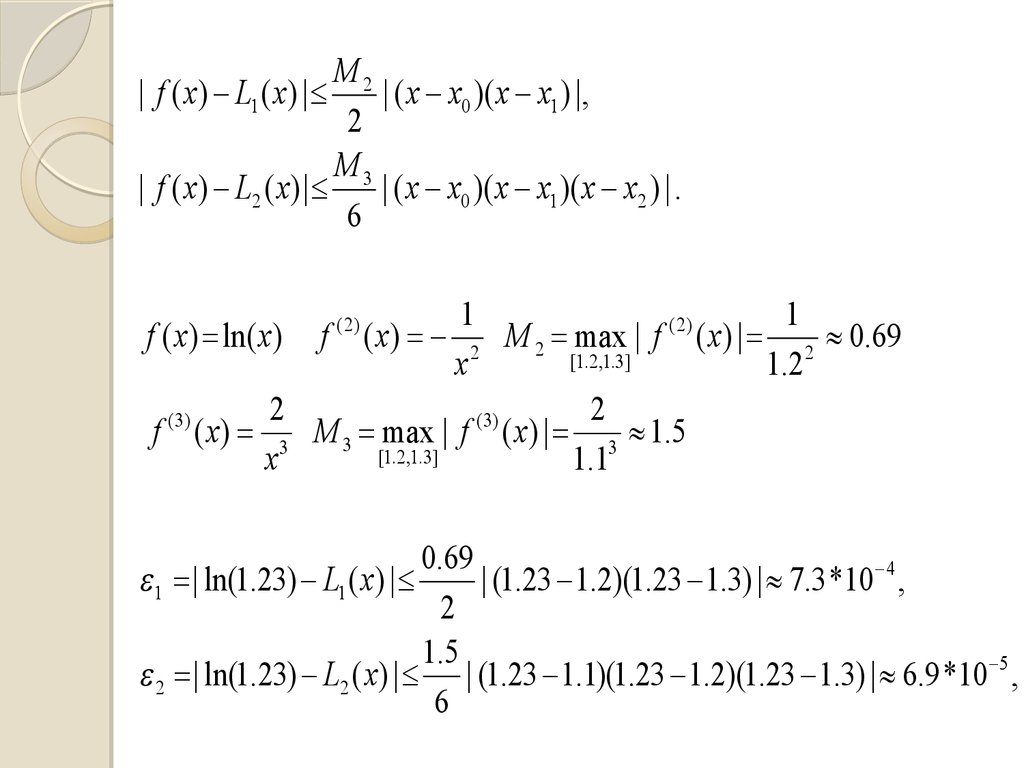



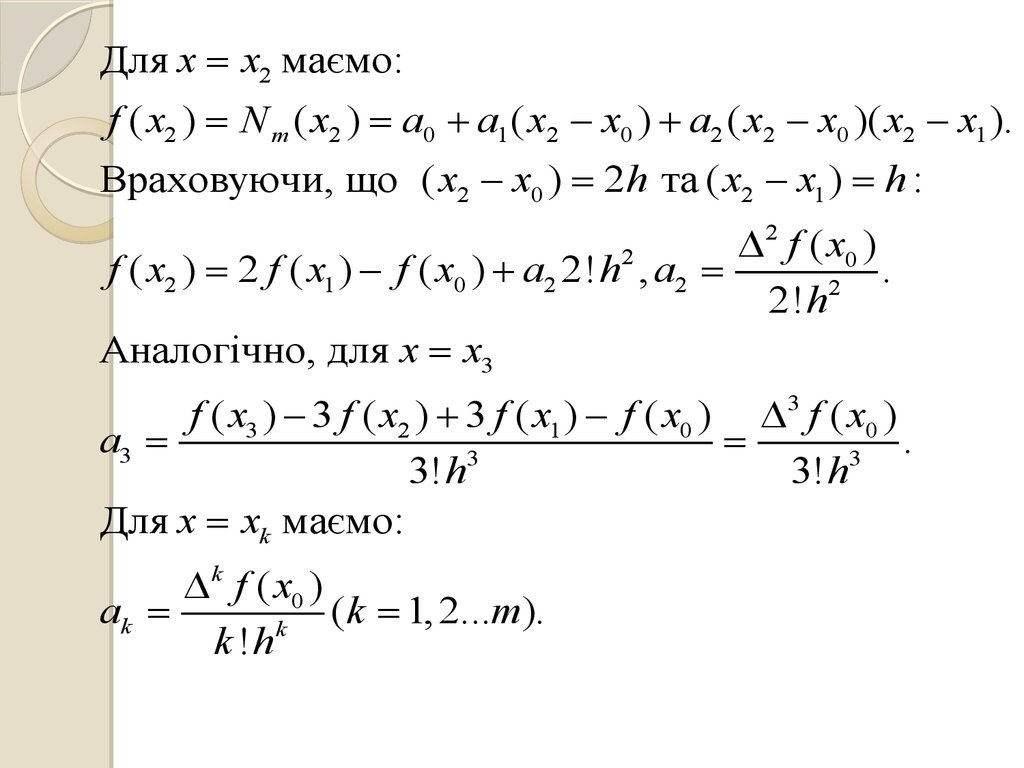


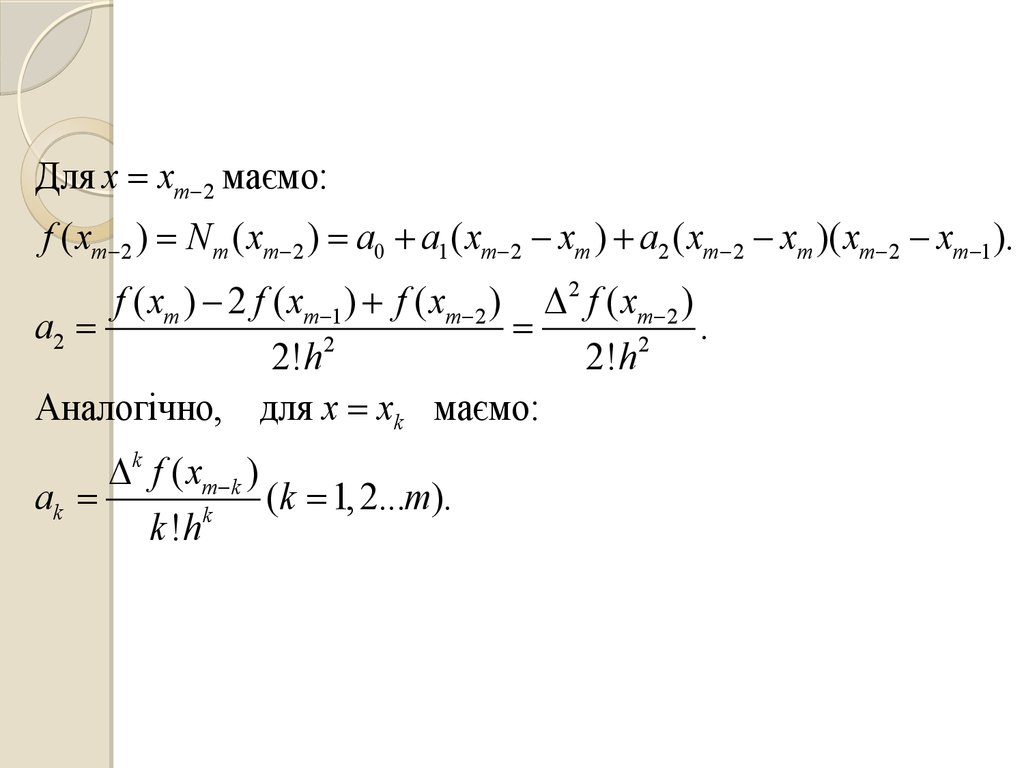

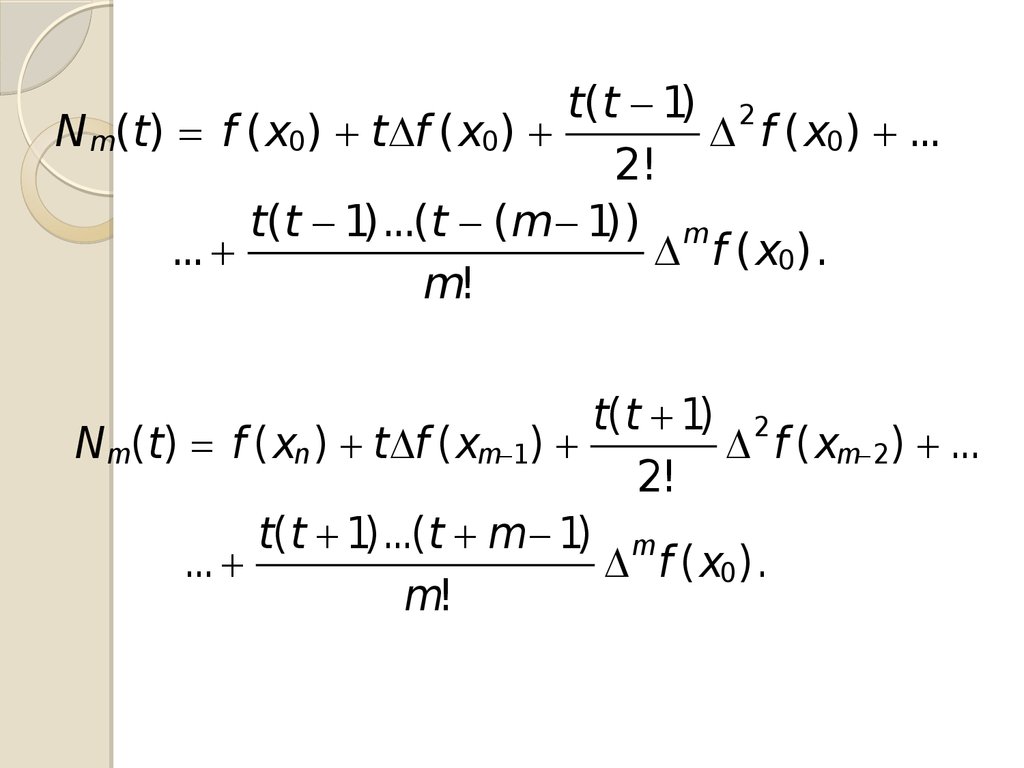

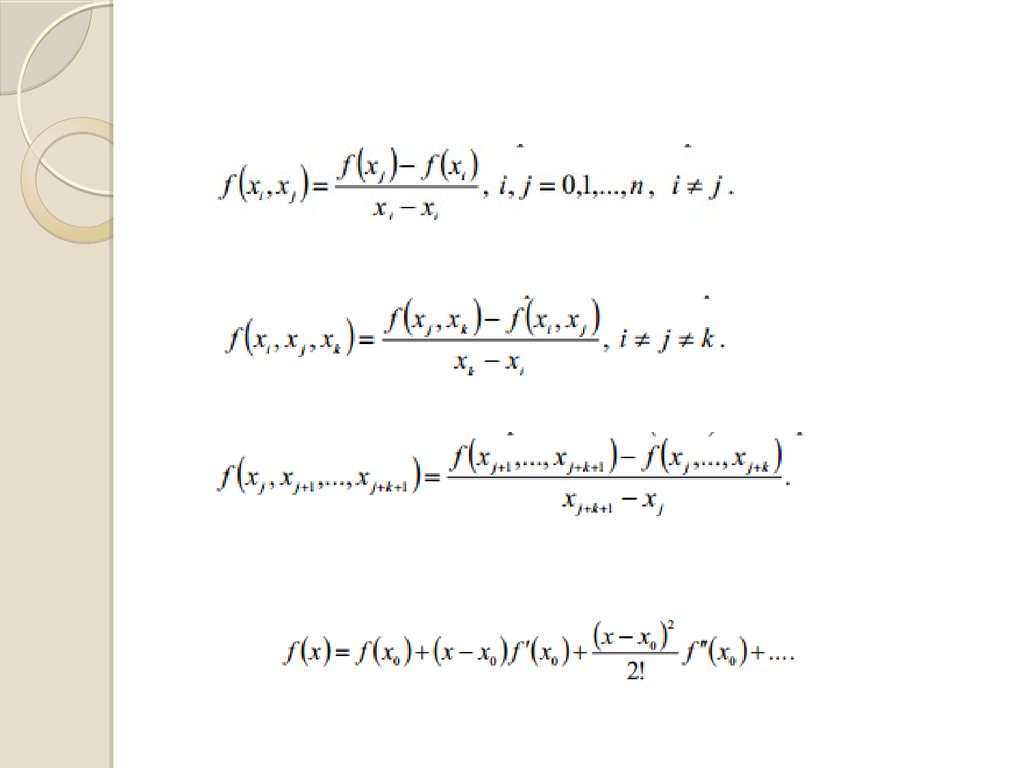









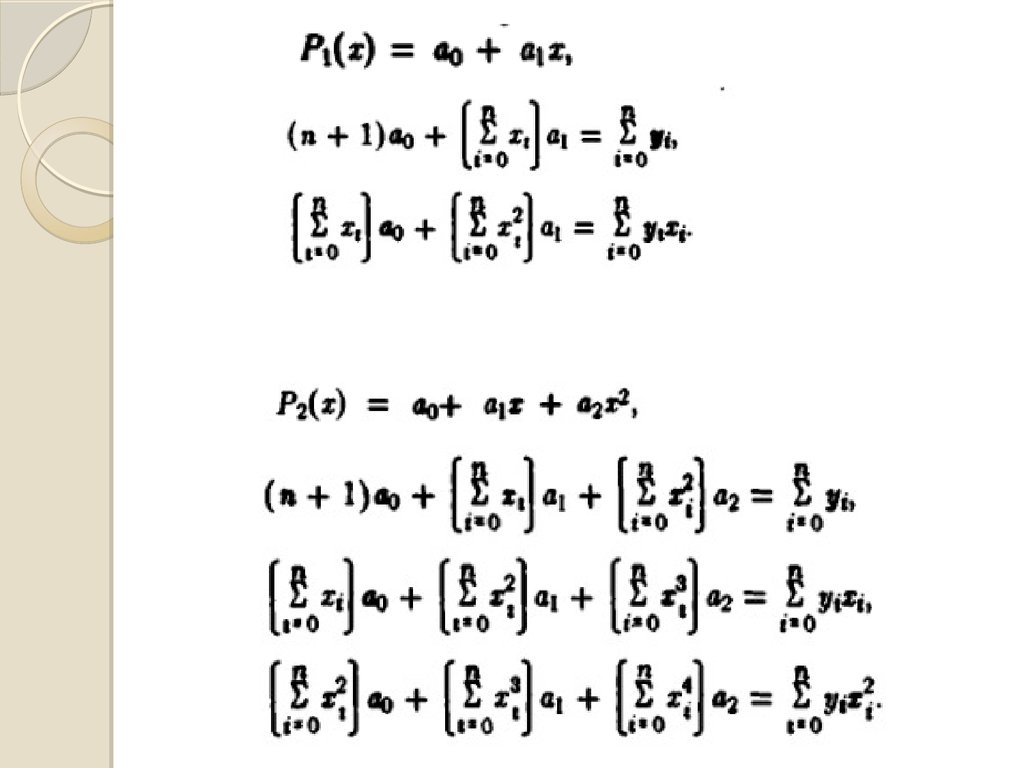

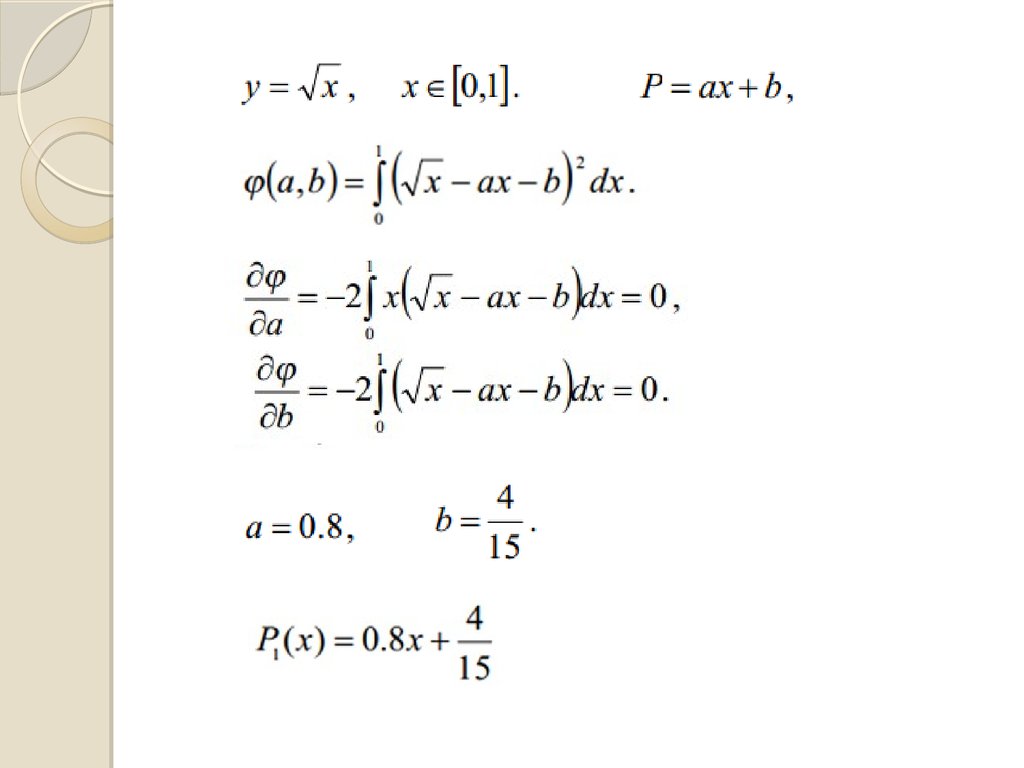
 mathematics
mathematics








