Лекция 6-24-25 Аналитика на плоскости

1. Математика

Лекция 6
Аналитическая геометрия

2.

Линии на плоскости. Уравнения прямой на плоскости
Линия на плоскости часто задается как множество точек,
обладающих некоторым только им присущим геометрическим
свойством.
Например, окружность – множество точек плоскости
равноудаленных от некоторой фиксированной точки О.
Уравнение линии (кривой) на плоскости: F(x, y)=0 (*).
Уравнению (*) удовлетворяют координаты (x, y) каждой точки
линии и не удовлетворяют координаты любой точки, не лежащей
на этой линии.
Задача о нахождении точек пересечения двух линий сводится
к решению системы уравнений: F1 ( x, y ) 0,
F2 ( x, y ) 0.

3.

Простейшей из линий является прямая.
Рассмотрим различные способы задания прямой на плоскости.
1. Уравнение прямой с угловым коэффициентом
( y y0 ) k ( x x0 ) или y kx b, (1)
где М0(х0, у0) – точка на прямой, k=tg , - угол между прямой и
положительным направлением оси Ох, b=у0 kх0, |b| - расстояние
от точки пересечения прямой и оси Оу до начала координат.
Если прямая проходит через О, то уравнение: у=kx.
Уравнение прямой, параллельной оси Ох: у= у0 (k=0).
Уравнение прямой, параллельной оси Оу: x=x0 ( = /2).

4.

2. Общее уравнение прямой
Рассмотрим уравнение 1 порядка: Ax+By+C=0, (2)
где A2+B 2 0.
Покажем, что это уравнение прямой.
C
Если B=0, то уравнение (2): Ax+C=0 x ( A 0).
A
Получили уравнение прямой, параллельной Оу.
A
C
Если B 0, то уравнение (2): y x уравнение с угловым
B
B
коэффициентом.
Уравнение (2) называется общим уравнением прямой (l).

5.

Замечание.
Любое уравнение первого порядка на плоскости определяет
прямую и наоборот, любая прямая на плоскости определяется
уравнением первого порядка.
3. Уравнение прямой, проходящей через две данные точки
Пусть M 1 ( x1 , y1 ) l , M 2 ( x2 , y2 ) l.
Возьмем произвольную точку на прямой M(x, y) и найдем
векторы M1M {x x1 , y y1}, M 1M 2 {x2 x1 , y2 y1}.
Так как M 1M M 1M 2 , то
x x1
y y1
.
x2 x1 y2 y1
(3)

6.

4. Уравнение прямой в отрезках
Пусть прямая (l) отсекает на осях Ох и Оу отрезки а и b
соответственно. Тогда M 1 (a,0) l , M 2 (0, b) l.
По уравнению (3): x a y 0 x 1 y
0 a b 0
a
b
x y
или 1. (4)
a b
5. Уравнение прямой, проходящей через данную точку
перпендикулярно данному вектору
Пусть M ( x0 , y0 ) l , n ( A, B) l.
Возьмем произвольную точку на прямой M(x, y) и найдем вектор
M 0 M {x x0 , y y0 }.

7.

Так как M 0 M l , n l , то M 0 M n M 0 M n 0.
Тогда А( x x0 ) B( y y0 ) 0. (5)
Уравнение (5) можно записать в виде Ax By C 0,
где С Аx0 By0 , т.е. уравнение (5) приводится к виду (2) .
Вектор n ( A, B) l нормальный вектор прямой.
Вектор l ( B, A) l направляющий вектор прямой.

8.

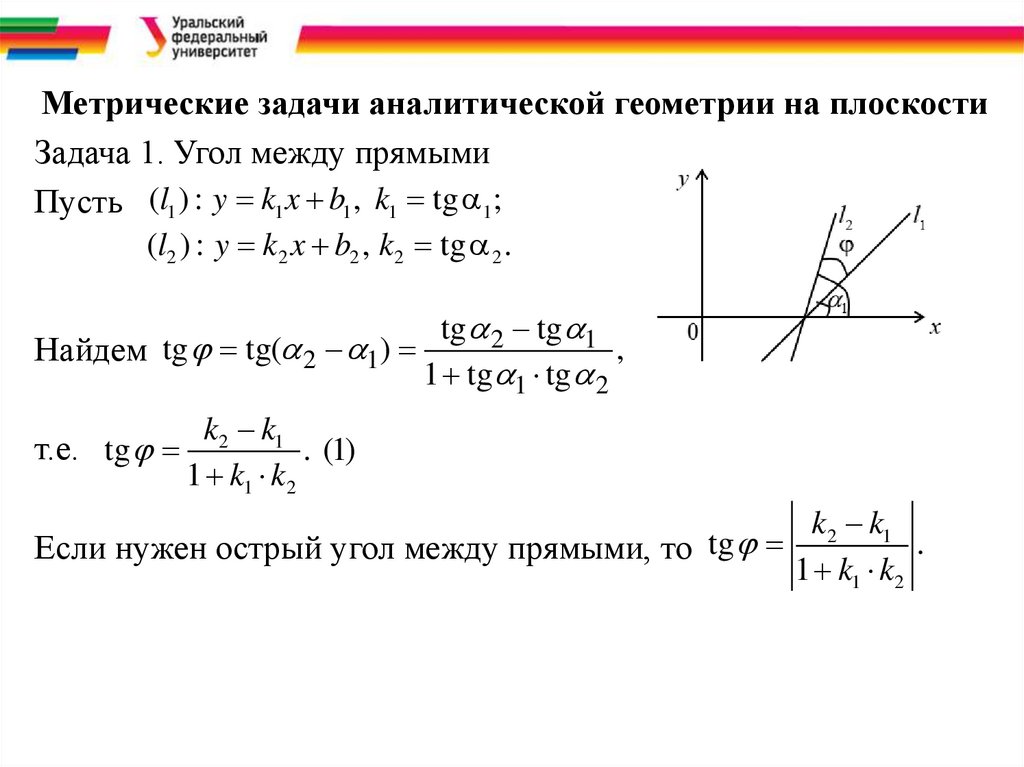
Метрические задачи аналитической геометрии на плоскости
Задача 1. Угол между прямыми
Пусть (l1 ) : y k1 x b1 , k1 tg 1;
(l2 ) : y k2 x b2 , k2 tg 2 .
tg 2 tg 1
,
Найдем tg tg( 2 1)
1 tg 1 tg 2
т.е. tg
k2 k1
. (1)
1 k1 k2
k2 k1
.
Если нужен острый угол между прямыми, то tg
1 k1 k2

9.

Задача 2. Расстояние от точки до прямой
Пусть (l ) : Ax By C 0; M 0 ( x0 , y0 ) l.
Расстояние d (M 0 , l ) прn ММ 0 , где M(x, y) произвольная точка
прямой (l), n ( A, B) нормальный вектор прямой.
ММ 0 n ( x0 x) A ( y0 y ) B
Тогда d ( M 0 , l )
2
2
|n|
A B
Ax0 By0 ( Ax By )
A B
2
2
M l Ax By C
Таким образом, d ( M 0 , l )
Ax0 By0 C
A B
2
2
. (7)
Ax0 By0 C
A B
2
2
.

10.

11.

Пример. Точка A(2, 5) является вершиной квадрата, одна из
сторон которого лежит на прямой х 2у 7=0. Вычислить площадь
этого квадрата. Найти уравнения прямых, на которых лежат
остальные стороны квадрата.