Similar presentations:
Основы биомеханики. Механические движения. Поступательное и вращательное движения. Деформация
1. ОСНОВЫ БИОМЕХАНИКИ
МЕХАНИЧЕСКИЕ ДВИЖЕНИЯ. ПОСТУПАТЕЛЬНОЕ ИВРАЩАТЕЛЬНОЕ ДВИЖЕНИЯ. ДЕФОРМАЦИЯ.
ЗАКОН ГУКА. УПРУГАЯ И ПЛАСТИЧНАЯ
ДЕФОРМАЦИЯ
ЗАДАЧИ, ОБЪЕКТЫ И МЕТОДЫ БИОМЕХАНИКИ.
ЗНАЧЕНИЕ БИОМЕХАНИКИ ДЛЯ МЕДИЦИНЫ
СВОЙСТВА БИОЛОГИЧЕСКИХ ТКАНЕЙ.
ВЯЗКОУПРУГИЕ, УПРУГОВЯЗКИЕ И
ВЯЗКОПЛАСТИЧНЫЕ СИСТЕМЫ. МОДЕЛЫ
ДЕФОРМАЦИИ ВЯЗКОУПРУГИХ ТЕЛ. МЕХАНИЧЕСКИЕ
СВОЙСТВА МЫШЦ, КОСТЕЙ, КРОВЕНОСНЫХ
СОСУДОВ, ЛЁГКИХ
ЭРГОМЕТРИЯ. МЕХАНИЧЕСКИЕ СВОЙСТВА ТКАНЕЙ
ОРГАНИЗМА
2.
ωR
3.
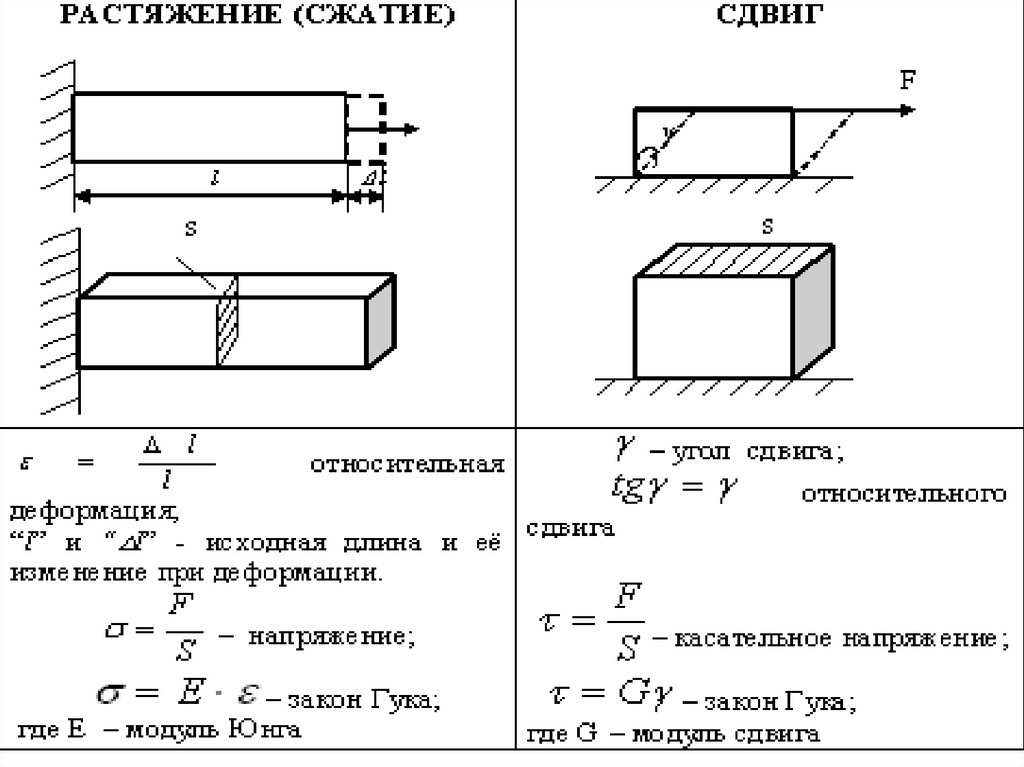
Изменение взаимного положенияточек называют деформацией.
Мерой деформации служит
относительная деформация ,
где l - первоначальное значение
величины, характеризующей
деформацию, а l - изменение этой
величины при деформации.
l
l
4.
5.
Напряжением называют силуупругости, отнесенную к площади
поперечного сечения тела:
Fупр
S
Упругие
деформации
подчиняются
закону
Гука,
согласно
которому
напряжение
пропорционально
относительной деформации:
l l
E ,
l
l
E
где Е - модуль
упругости
6.
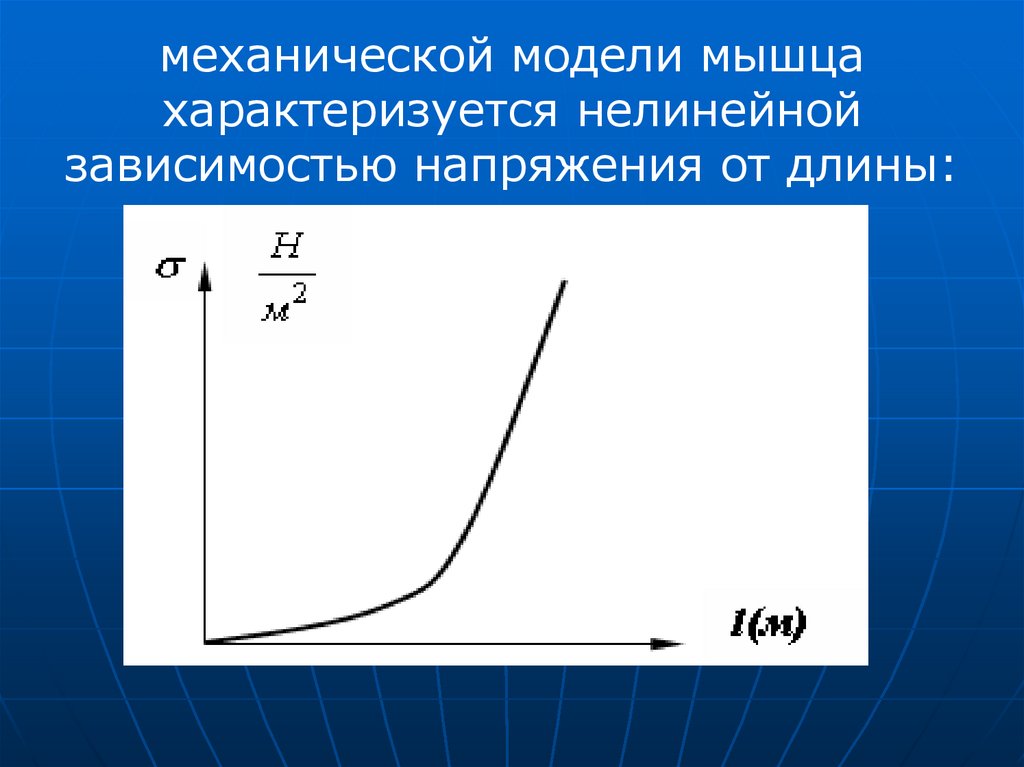
Закон Гука обычно справедлив прималых деформациях. Экспериментальная
кривая растяжения приведена на
рисунке.
7.
Кривая зависимости напряженияот деформации имеет три точки
предельности: 0А - соответствует
упругим деформациям, точка В–
предел упругости, участок СД–
предел текучести, начиная с
которого деформация возрастает
без увеличения напряжения, т.е.
предел прочности — максимальное
напряжение перед разрушением
тела.
8.
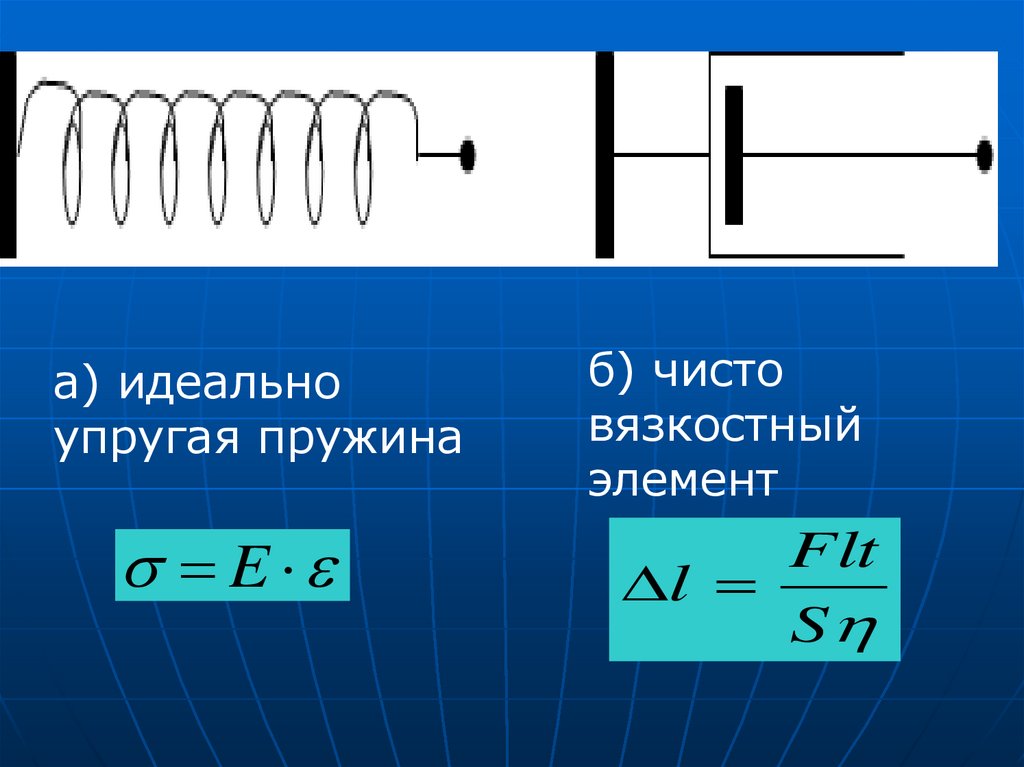
а) идеальноупругая пружина
б) чисто
вязкостный
элемент
E
Flt
l
S
9.
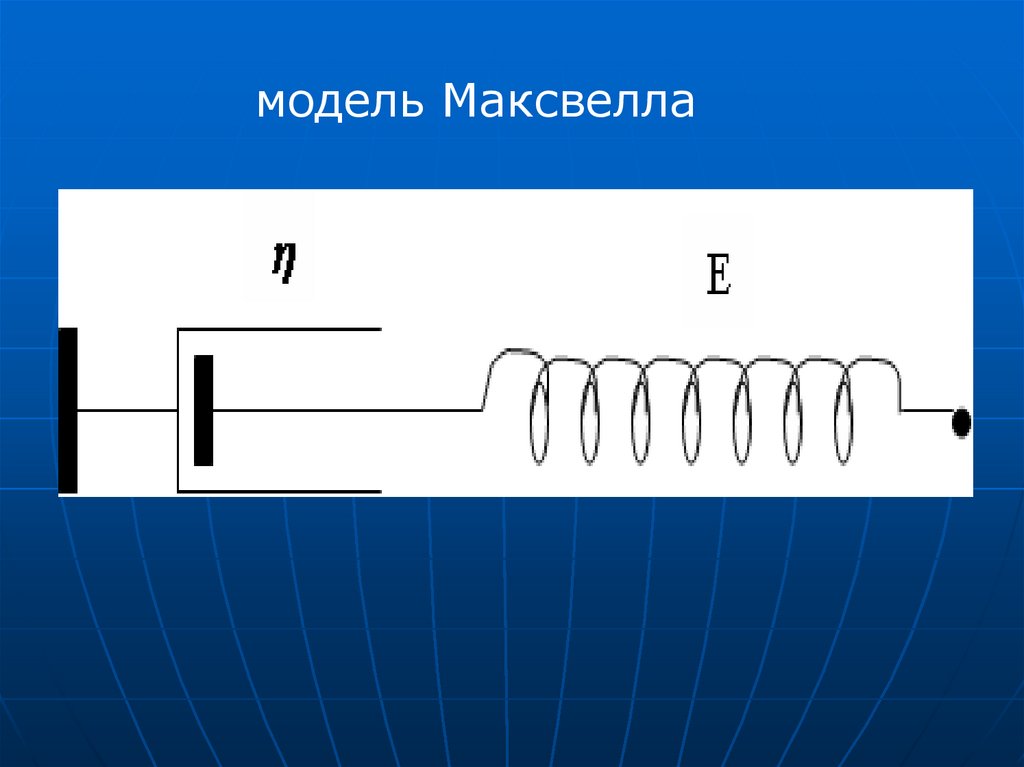
Вязкоупругая деформацияFсопр=r∙dx/dt
Если вместо силы Fсопр взять ее
отношение к площади, т.е.
напряжение σ, вместо коэффициента
трения η коэфф. вязкости, вместо
смещения тела — относительное
удлинение, то уравнение имеет вид:
σ=η∙dε/dt
Напряжение зависит и от скорости
перемещения поршня: σ~dε/dt .
10.
Кость.Половину объема и 2/3 часть
массы кости составляет
минеральное вещество
гидроксилапатит:
3Са3(РО4)2∙Са(ОН)2;
Плотность костной ткани:










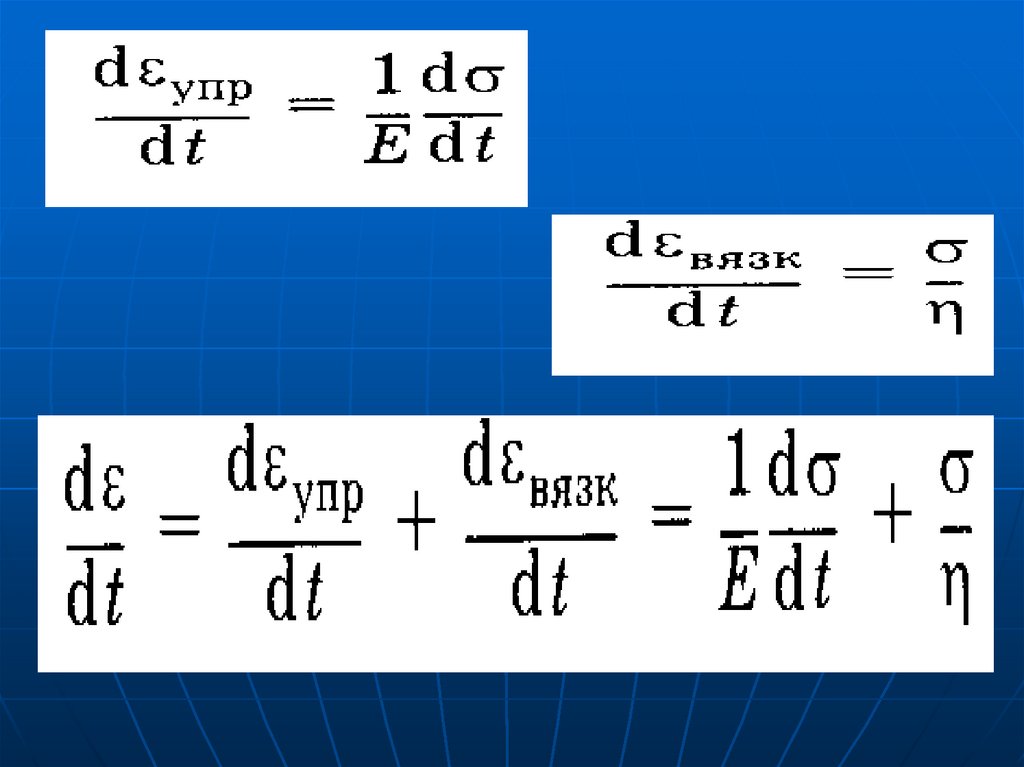






















 physics
physics








